利用本质矩阵进行低空无人机影像位姿恢复的研究
2018-05-04张晶晶吴良才艾海滨赵栋梁
张晶晶,吴良才,艾海滨,许 彪,赵栋梁
(1. 东华理工大学,江西 南昌 330013; 2. 中国测绘科学研究院,北京 100830; 3. 国家测绘地理信息局第三地形测量队,黑龙江 哈尔滨 150025)
恢复影像的外方位元素是摄影测量技术中尤为关键的一步[1],进行经典的连续像对相对定向时,需明确影像的航带信息及影像基线方向(通常为影像列方向),并给定定向元素的初始值(通常为0),根据共面条件利用最小二乘原理迭代求解未知数[1-2]。国外的Helava系统、Image Station系统和Inpho系统,国内的PixelGrid系统、VirtuoZo系统、JX-4系统等,都是采用传统摄影测量理论的空三加密软件。近些年,因无人机机动性高、数据采集便捷和容易转场等优点,无人机摄影测量已成为当前摄影测量的重要方式之一[3],但由于无人机质量轻、体积小、携带非量测数码相机,相机镜头的安置方式发生变换,导致航空影像姿态角度大、基线方向不再是影像列方向,传统的连续像对相对定向不再满足这类影像的处理要求。近些年兴起的计算机视觉相关技术,引起了摄影测量领域诸多学者的广泛关注[4-5],与传统摄影测量方法不同,计算机视觉方法只需影像间的匹配点对就可恢复单像对的相对运动,进而恢复多张影像的位姿,如当前广泛使用的Agisoft PhotoScan、Pix4Dmapper、Smart3DCapture等软件就是利用计算机视觉技术恢复互联网图片、手机照片及无POS数据的航空影像位姿的方法进行三维重建的。但计算机视觉方法仍存在一些缺陷,尤其是渐进式重建算法(incremental structure from motion)[6-8],对初始像对的选取要求高,最佳的添加影像难以确定,计算复杂度大,当相机轨迹过长时会由于误差累积导致重建几何变形。但传统摄影测量方法不存在该问题,因此本文将计算机视觉中的本质矩阵与经典的连续像对相对定向相结合来处理低空无人机影像。该方法在避免计算机视觉方法缺陷的同时,能够快速确定基线方向,并且恢复影像外方位元素。
1 基于本质矩阵的无人机影像位姿恢复
1.1 本质矩阵恢复相机位姿
对极几何(epipolar geometry)反映了三维空间中同一物体两幅不同影像间内在的射影关系,独立于景物场景结构,只依赖于相机的内参数和相对运动[9-11]。如图1所示,影像A和B分别表示以O和O′为摄影中心的空间中三维点M的两幅图像,x和x′为投影点。左片投影点x反向投影在空间中形成一条射线,由摄影中心O和点x确定,投影到x的空间点M必然落在该射线上,其在B中被映射成一条直线l′,因此M在B上的投影点x′必然落在l′上。

图1 对极几何
本质矩阵E是对极几何的表达形式,假设R为左相机到右相机的旋转矩阵,t为两个相机间的平移量,根据共面条件,可推出本质矩阵E的表达式为
E=[t×]R
(1)
式中,[t×]为反对称矩阵。E可由5对归一化图像坐标直接计算[12-13],但影像对的匹配点中通常含有误匹配,因此估计E时需采用RANSAC算法[14-16]逐步剔除粗差点,取得最优模型。估计到E后,对其进行奇异值分解,并且通过空间点同时在两个相机前方交会的方法消除模糊解,就可以恢复两幅影像的相对运动(相差一个尺度因子)。
1.2 基于本质矩阵的连续像对相对定向
相对定向的目的是恢复摄影时相邻两个摄影中心的相对位置关系[1]。本文以本质矩阵恢复单像对相对位姿为基础,结合传统摄影测量方法恢复低空无人机影像的外方位元素,具体步骤如下:
(1) 相对定向。用本质矩阵恢复两幅影像旋转矩阵Rcv和平移量tcv。计算机视觉与摄影测量采用的坐标系分别为左右手坐标系,两个坐标系中平移量的关系为
(2)
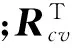
(3)
给影像基线分量By赋定值,其余分量Bx、Bz按照比值赋值为
(4)
将以上平移量的值作为经典连续像对相对定向线元素的初始值,角元素(φ,ω,κ)初始值均设为0,根据共面方程利用最小二乘原理趋近求解定向元素。
(2) 构建自由区域网。每一像对进行相对定向后,各模型间相差一个缩放因子,故需用公共点在相邻模型间的点位,同样计算后一模型相对于前一模型的比例因子,进行模型连接,并且通过空间前方交会计算同名点的三维坐标,完成自由比例尺单航带网的构建。单航带网构建完成后,每个航带的坐标系是独立的,要构建区域网需统一各航带模型[17]。相邻航带的公共点满足如下关系
(5)

2 试验与分析
2.1 试验数据
为验证本文定向方法的有效性,采用以下两组影像数据集进行试验。影像集一为嫩江影像,该影像由Sony ILCE-7R(相机参数可见表1)于2013年3月24日采集,取其中74张影像作试验,影像航向重叠度约为85%,旁向重叠度约为90%,飞行高度约为220 m。影像集二为四川影像数据(相机参数见表1),该影像共有52张影像,航向重叠度约为75%,旁向重叠度约为40%。部分影像如图2所示。

图2 影像数据集

试验区域影像数/幅像幅尺寸/像素像主点/mmwhx0y0相机焦距/mm像元尺寸/mm嫩江区域74736049120.01710.104655.36250.00488四川区域52374456160035.48810.0064
为验证结果精度,本文使用物方点在影像上的重投影点与量测点之间的距离平方和评判算法的结果精度,并将本文算法得到的精度与用计算机视觉技术中的Sfm算法精度进行比较。重投影误差计算公式为
(6)

2.2 结果与分析
嫩江影像集与四川影像集中部分影像的相对外方位元素分别见表2和表3,包括用本质矩阵恢复的相对平移量和用本文定向算法恢复的外方位元素。从表2中本质矩阵恢复的单像对相对运动结果得到嫩江影像的基线方向为y方向,x方向和z方向分量与基线的比值分别约为0.425和0.083;同样从表3中得到四川影像的基线方向为x方向,y方向和z方向分量与基线的比值分别约为0.032 8和0.082;将上述数据按照1.2节所述进行处理可成功定向并得到自由区域网,证明从相对平移量确定的影像基线是正确的。因为从本质矩阵分解得到的单像对的相对运动,在相差一个尺度因子的情况下,平移量的3个分量可表示右相机相对于左相机在3个坐标轴上的平移,故可从平移量的分量值快速确定影像基线方向。
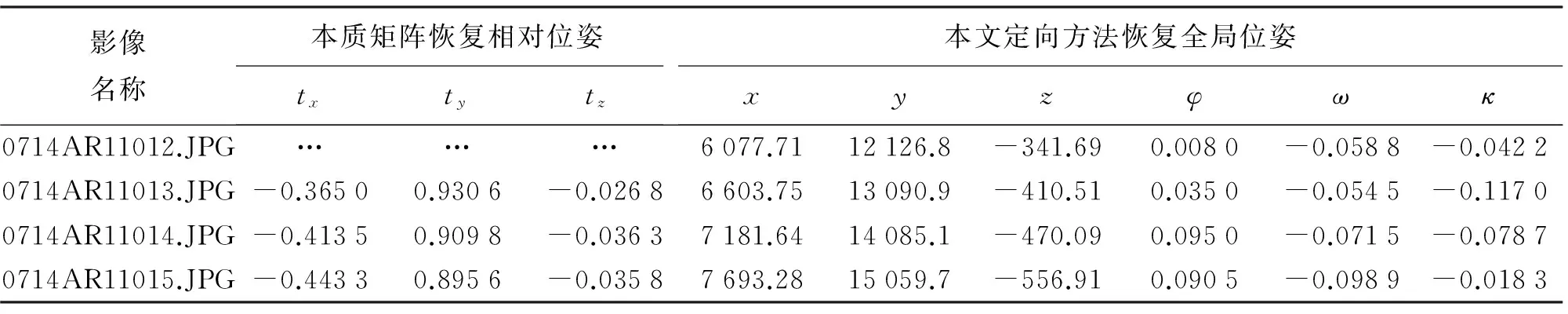
表2 嫩江影像数据集中部分影像位姿
试验结果精度见表4,从中可以看出,用本文所提方法恢复两个影像集的外方位元素得到的重投影误差分别为0.432和0.205 7个像素,都在1个像素以内。而用Sfm算法得到的精度都在3个像素以上。经典的连续像对相对定向是一个在给定定向元素初始值的基础上逐步趋近求解的过程,有较好的初始值,就会快速收敛于正确值。本文根据本质矩阵得到像对的相对平移量分量之间的关系给定连续相对定向线元素的初始值,初始值较接近于最终值,故可得到较好的精度。而且本文方法的后续处理类似于传统摄影测量将非线性等式化为线性等式,利用最小二乘原理求解,可得到精确稳定的结果。Sfm算法是基于非线性等式,采用RANSAC方法选取适当的代价函数,进行矩阵分解,结果依赖于初始特征点分布及其匹配的质量,并且试验中Sfm算法所用的相机参数是从影像的EXIF信息中提取的概略值,故本文方法的精度高于Sfm算法的精度。

表3 四川影像数据集中部分影像位姿

表4 试验结果精度
图3为空间前方交会得到的稀疏三维点云。

图3 影像重建结果
3 结 语
为了能够快速确定影像的基线方向,恢复低空无人机影像的外方位元素,本文以计算机视觉中的相对定向为基础,与经典的摄影测量结合恢复影像位姿。试验证明,该方法能够快速确定影像的基线方向,恢复影像的外方位元素,得到三维点云,而且在精度上,重投影误差在1个像素以内。本文算法初步尝试将计算机视觉技术与传统摄影测量技术相结合,顾及航空影像的有序性和结构性特点,结合计算机视觉中定向算法的通用性,能够利用上述算法较好地估计影像的位姿参数。但是对于各类型影像的稳健性还有待提高,大规模影像数据的定向试验有待进一步研究。
参考文献:
[1] 张祖勋.数字摄影测量与计算机视觉[J].武汉大学学报(信息科学版),2004,29(12):1035-1039.
[2] 张力,艾海滨,许彪,等.基于多视影像匹配模型的倾斜航空影像自动连接点提取及区域网平差方法[J].测绘学报,2017,46(5):554-564.
[3] 王湘文,于启升,王雅鹏.无人机低空摄影测量系统在大比例尺地形图中的应用[J].地矿测绘,2013,29(1):34-36.
[4] 孙敏.多视几何与传统摄影测量理论[J].北京大学学报(自然科学版),2007,43(4):453-459.
[5] 张祖勋.数字摄影测量与计算机视觉[C]∥全国数字近景摄影测量学术研讨会.[S.l.]:武汉,2004.
[6] SCHONBERGER J L,FRAHM J M.Structure-from-motion Revisited[C]∥Proceedings of the CVPR.[S.l.]:CVPR,2016.
[7] SCONBERGER J L,FRAUNDORFER F,FRAHM J M.Structure-from-motion for MAV Image Sequence Analysis with Photogrammetric Applications[J].International Archives of the Photogrammetry Remote Sensing & S,2014,XL-3(3):305-312.
[8] WU C.Towards Linear-time Incremental Structure from Motion[C]∥International Conference on 3dtv-Conference.[S.l.]:IEEE,2013:127-134.
[9] ZISSERMAN A.Multiple View Geometry in Computer Vision[J].Kybernetes,2003,30(910):1865-1872.
[10] FO W,WROBEL B P.Photogrammetric Computer Vision[M].[S.l.]:Springer International Publishing,2016.
[11] 陈登,林卉,苏天路,等.多视几何理论辅助的无人机低空摄影测量空三加密[J].测绘通报,2017(6):26-30.
[12] DAVID R.An Efficient Solution to the Five-point Relative Pose Problem[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2004,26(6):756-770.
[13] 王文斌,刘桂华,刘先勇,等.本质矩阵五点算法伪解的两种剔除策略[J].光电工程,2010,37(8):46-52.
[14] MOISAN L,MOULON P,MONASSE P.Fundamental Matrix of a Stereo Pair,with a Contrario Elimination of Outliers[J].Image Processing on Line,2016,6(6):89-113.
[15] 甄艳,刘学军,王美珍.一种改进RANSAC的基础矩阵方法[J].测绘通报,2014(4):39-43.
[16] MOISAN L,MOULON P,MONASSE P.Automatic Homographic Registration of a Pair of Images,with a Contrario Elimination of Outliers[J].Image Processing on Line,2012,2(5):56-73.
[17] 王解先.七参数转换中参数之间的相关性[J].大地测量与地球动力学,2007,27(2):43-46.
