高速公路分车道荷载差异及其响应特性

周军勇， 石雪飞， 阮 欣， 涂辉招

(1. 同济大学 土木工程学院，上海 200092；2. 同济大学 交通运输工程学院，上海 201804)

随着我国交通基础设施建设的快速发展，高速公路通车里程已超过13万km.目前，高速公路都实施了按车型分车道行驶的规定，这大大提高了安全保障和运行效率；同时，也使得各个车道中运行车辆、实际荷载及其作用响应不均一，给交通基础设施的设计和运营管养带来新的问题[1-2].目前，在桥梁的相关设计规范中，尚未对各个车道的荷载进行区分定义，而仅考虑分车道同时出现不利荷载的概率折减[3-4]，并没有全面反映分车道行驶所带来的车道荷载及其响应的差异.

近年来，基于大量动态称重(weigh-in-motion, WIM)数据的积累[2,5-6]，许多学者开始研究分车道行驶带来的各种影响：Blab等[7]通过实测重车数据，分析了重车载重及其横向位置偏移对道路面层厚度设计的影响；Huang等[8]认为多肋式梁桥的静动力响应受到分车道车辆荷载差异性的影响，导致内外梁受力显著不同；Enright等[9]指出分车道荷载差异会显著影响相遇重车的极值效应水平；Zhou等[10]通过WIM数据评估了混凝土和钢桥面板的疲劳寿命，指出分车道荷载差异性使得各车道的结构寿命显著不同，可以进行结构优化达到一致疲劳寿命；阮欣等[2]提出四车道高速公路的分车道荷载差异对路面PCI(pavement condition index)指数和中小跨径桥梁荷载响应的影响显著，提出设定不同的管养策略.综上可知，多车道中分车道荷载的差异会对结构安全和使用寿命产生显著影响，因此，基于WIM测试数据呈现我国高速公路车辆的分车道交通行为、荷载分布及其响应特性的规律，意义显著.

选取实测的我国高速公路单向两车道、三车道和四车道各28 d的WIM数据，数据通过TDXWIN设备采集[11]，研究不同车道数量下分车道的交通行为、荷载分布及其产生的结构响应特性，为多车道交通管理、车辆荷载模型建立及结构设计优化提供参考.

1 分车道交通与荷载差异

多车道高速公路中分车道的名称标识及WIM设备布置如图1所示，其中车道1是道路内侧供超车行驶的车道.

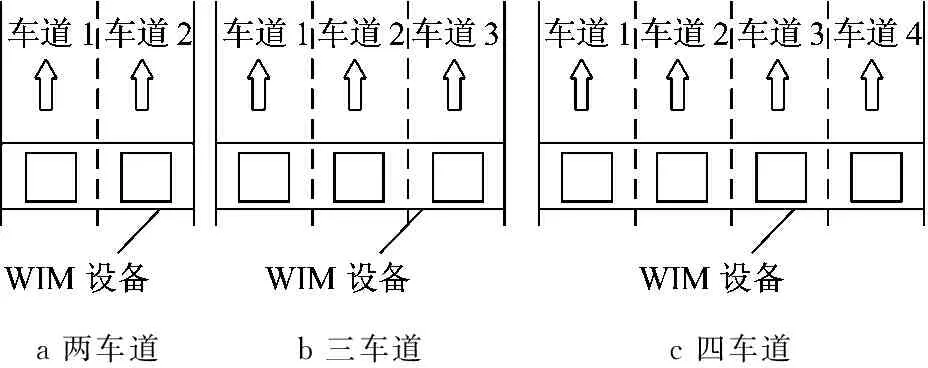
a两车道b三车道c四车道

图1多车道高速公路中的分车道

Fig.1Lanenamelabelformulti-lanefreeway

1.1 合理统计时长的确定

实测车辆数据具有变异性，因此需要确定合理的统计时长，使各类车辆统计参数趋向稳定.这里以车型(按轴数分类)的车道选择概率为研究参数，分析其随累积时长的变化关系，当参数变化很小并趋向稳定数值时，就可以认为是达到了合理的统计时长.

图2以三车道为例给出了各种车型对不同车道的选择概率随累积天数的变化关系.由图可见，各类车型对车道的选择具有明显的差异，例如五轴车选择车道3的概率达到0.75，对车道2的选择概率仅为0.25，而对车道1选择概率接近于零.此外，各车型的车道选择概率在累积10 d内波动显著，累积10～20 d内具有一定变异，累积20 d后基本趋于稳定.

对不同地点的其他车道的统计也可以得到类似结论，因此可以认为，20 d是一个合理的统计时长，后续各种分析应至少采用20 d的WIM数据.

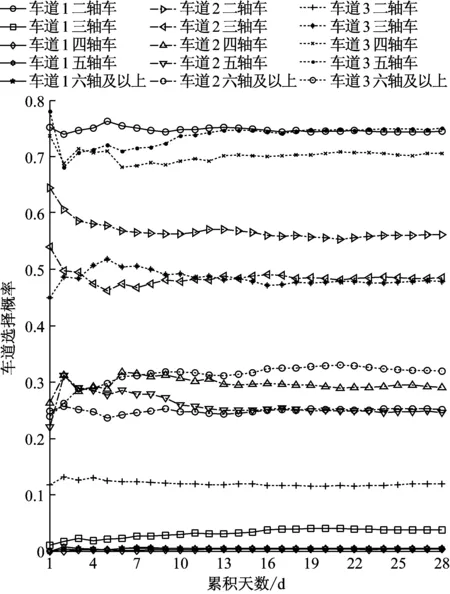
图2 三车道情况下各车型对车道选择概率随累积天数的变化规律

Fig.2Rulesofvehiclelane-choosingprobabilitiesalongwithcumulativedayswithanexampleof3-lanefreeway

1.2 分车道交通行为的差异

车辆的交通行为主要包括：①单车道内的车速选择与跟驰方式，②多车道内的车道选择与变道方式.交通行为直接影响宏观层面的交通流量与交通密度，从而影响荷载.比如，在自由通行状态下，车辆往往追求更高的驾驶安全和行驶质量而不轻易变道和超车，使得各种类型的车辆在交通法规约束下根据其自身机动性能及装载特点往往倾向保持在特定车道行驶，从而成为这些车道中主要的组成车型.

表1和图3是累积时间28 d不同车道数量下的交通组成及各车型的车道选择概率分析.总体可知，

表1 不同多车道情况下各车型的组成概率Tab.1 Composite percentage of each vehicletype of various multiple lanes

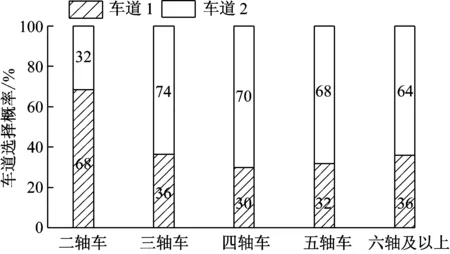
a 两车道

b 三车道

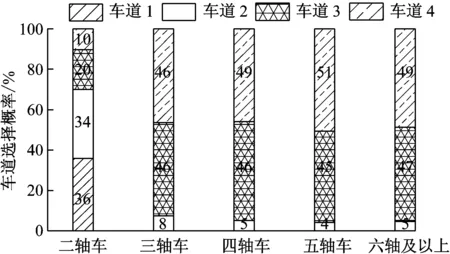
c 四车道图3 多车道中各车型对分车道的选择概率Fig.3 Comparison of vehicle lane-choosingprobabilities in multi-lane freeway

在总的交通量中，二轴车占最主要成分，近80%以上，大型车辆(六轴及以上)占4.0%～8.5%.而对各车型的车道选择特性的统计表明：①两车道中二轴车选择车道1概率为车道2的2倍多，而多轴车选择车道2概率是车道1的2倍多；②三车道中二轴车主要选择内侧2个车道行驶，多轴车基本不进入内侧车道1，而大型车选择车道3的概率是车道2的3倍多；③四车道中二轴车选择车道1和2的概率等同，多轴车不进入车道1，而大型车对车道2、3、4概率选择均等.各种车型的车道选择特性显著影响了各车道的车型构成，进而对车道荷载及其荷载响应产生影响.

1.3 分车道交通流量的差异

各车型的车道选择概率使得分车道的宏观交通参数不同，如交通流量、速度和交通密度等.表2分析了不同车辆总重下的分车道交通流量比例.总体上内侧车道的交通流量都会显著高于外侧车道，但剔除轻型轿车(≥3.5 t)后，两车道中内外车道基本持平；三车道中车道1流量极低，车道2与3基本持平；四车道中车道3与4大体相同，车道2较低，车道1流量接近零.考虑重载车时(≥20 t)：两车道中车道2是车道1的2倍多；三车道中车道3是车道2的2倍多且车道1接近零；四车道中车道3与4基本持平，车道1与2接近零.超重车(≥55 t)选择车道的规律基本与重载车一致.车道交通流量的对比表明：各车道不仅总体交通流量存在差异，高载重车辆的出现频次也差别很大，直接影响分车道的荷载密集程度.

表2 多车道中分车道交通流量的对比Tab.2 Comparison of traffic volume among laterallanes in multi-lane freeway

1.4 分车道荷载的差异

多车道中各车型的车道选择使得分车道荷载分布存在差别，图4通过耿贝尔分布概率纸呈现了分车道的车辆车重分布，通过中位值(50.0%)、90.0%和99.9%分位值比较不同概率水平下分车道荷载的差异.

从车重中位值来看：两车道中内外车道基本相同(2.2 t)，说明轻型车占有50.0%以上比例；三车道中车道1和2基本相当(1.6 t)，而车道3显著高(17.1 t)，说明轻型车基本在车道1和2分布，车道3平均荷载水平显著大；四车道中车道1和2基本相当(1.1 t)，车道3(8.4 t)和车道4(11.3 t)依次增高，说明外侧两车道平均载重水平显著大于内侧2个车道.

a 两车道

b 三车道

c 四车道图4 多车道中分车道的车辆车重分布Fig.4 Distribution of vehicle load of each lanein multi-lane freeway

对比车重90.0%高分位值和99.9%超高分位值：两车道中车道2是车道1的1.2倍以上，并随分位值增大分车道差异性降低；三车道中，高分位值下各车道存在明显差别，但超高分位值下车道2和3趋于相同，并显著大于车道1(3倍以上)；四车道中，高分位值下各车道间存在明显差别且外侧两车道显著大于内侧两车道；超高分位值下外侧3个车道则显著高于车道1(6倍以上).

观察分车道中车辆车重的尾部趋势：两车道中内外车道趋于一致，差别并不显著；三车道中外侧2个车道趋于一致，并大于车道1；四车道中外侧3个车道差别不明显，但显著大于车道1.

各车型的车道选择特点使得分车道的交通流量和荷载存在明显差别.交通流量与荷载水平是车辆荷载响应的最显著影响因素[4,10].然而，由于车辆作用的随机性，基于交通流量和荷载水平难以定量推演荷载响应.以下分别从车重极值、荷载响应极值和荷载响应损伤累积3个层面研究分车道交通流量和荷载的差异对桥面结构局部设计、桥梁整体设计和桥梁疲劳设计的影响.

2 分车道车重极值特性

桥面结构的局部设计(如涵洞、伸缩缝、桥面板等)主要受单个车辆的载重影响.这里通过极值外推方法确定设计基准期内分车道的车辆荷载载重特征值.我国D60规范中汽车荷载标准是设计基准期100年最大值95%的概率保证率，对应于重现期1950年.以下将采用与此相同的标准.

根据经典极值理论，通过区组最大值的方法选取样本，当采样数量足够多时，这些最大值样本都可以用广义极值分布(generalized extreme value distribution, GEVD)进行描述，如式(1)[12].这里的分析中以天为区组，对各个车道每天最大载重样本进行GEVD拟合，确定的多车道中各车道外推载重极值如表3.

(1)

式中：x为车重；ξ,σ,μ分别是广义极值分布的形状参数、尺度参数和位置参数.

表3 多车道中分车道外推车辆载重极值Tab.3 Extrapolated extreme vehicle weight ofeach lane in multi-lane freeway

尽管3组数据由于测试地点的差异、外推载重极值的量值存在差别，但从同组数据的分车道外推结果及第1.4节的分析可以看出：①在两车道高速公路中，虽然车道1和2荷载水平存在差异，但外推载重极值差异不大.局部设计中可以选用相同的车重荷载模型.②在三车道高速公路中，虽然车道2和3相对车道1荷载水平高很多，但外推载重极值差异并不明显.局部设计中车道2和3可以选用相同车重荷载模型，而车道1需进行数值折减；③在四车道高速公路中，车道2、3、4的外推极值载重水平基本相当，且显著大于车道1的外推极值(2.3倍以上)；因此局部设计中车道2、3、4可以采用相同车重荷载模型，而车道1应该采用不同模型或进行折减.外推车重极值的上述特性与图4呈现的多车道车重荷载尾部走势吻合.

值得关注的是：外推的载重极值除四车道的车道1外，其余均大于我国规范的现有标准(55 t)，桥面局部构件设计中应考虑这一因素，以保证其安全与耐久.

3 分车道荷载响应极值特性

为分析分车道交通流量与荷载的差异对桥梁荷载响应的影响，计算了5～1 000 m不同加载长度的虚拟简支梁桥[13]在WIM自然车队作用下分车道跨中弯矩的荷载响应时程.

WIM系统采集的是断面交通及荷载数据；将WIM数据还原成空间有序排列车队时，还需要基于一定的假设，特别是对于长跨度的加载.这里，假定WIM车队保持采集时的车辆间距排列展开形成车队，认为在后车达到前车位置的时间段内后车保持恒定速度行驶，车辆间隔g=vi+1(ti+1-ti)-pi维持不变，如图5.WIM自然加载车队的构建方法及荷载响应计算过程如下：①推进时间步到t；②从t开始，假定前后车辆间距保持固定，进行同向多车道车辆合并，计算前后车的间距，然后拓展成原来的多车道车队，截取加载长度内的轴载序列；③将车队的轴载序列作用于影响线并计算荷载响应；④推进时间步到下一个t，并重复步骤②至④直到时间步长结束.

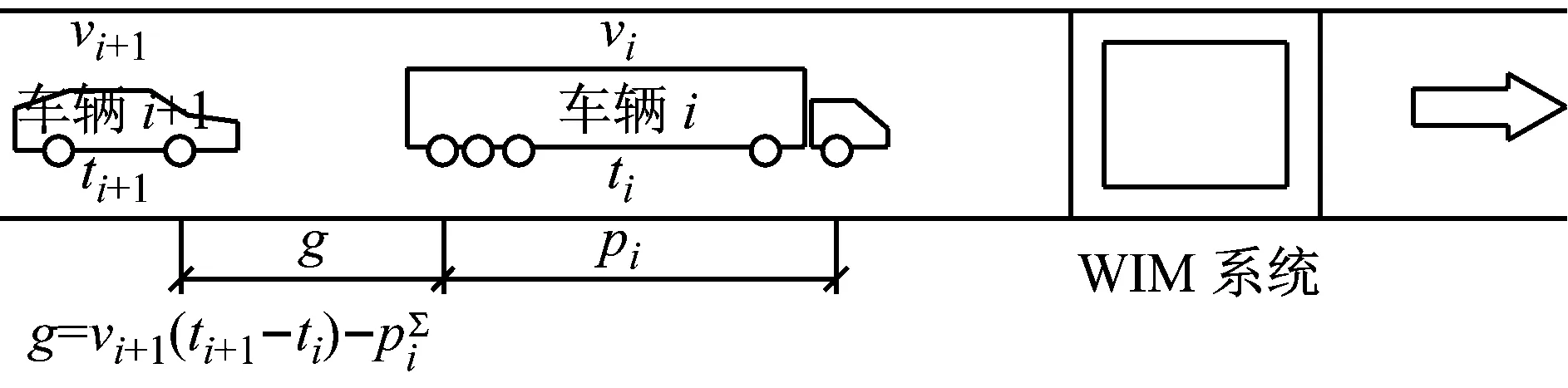
图5 WIM设备测试获取车队序列的图示Fig.5 Diagram of measured vehicle sequence throughWIM system

桥梁整体设计时主要关注构件的强度，而强度受车道荷载响应极值直接影响.计算分车道间荷载响应极值的比值(ratio of extreme lane load effect, REL)及其与加载长度的变化关系，如图6，以反映分车道荷载响应极值的差异.这里以WIM车队加载响应的98.0%分位值作为分车道荷载响应极值.

a 两车道(车道1与车道2)

b 三车道

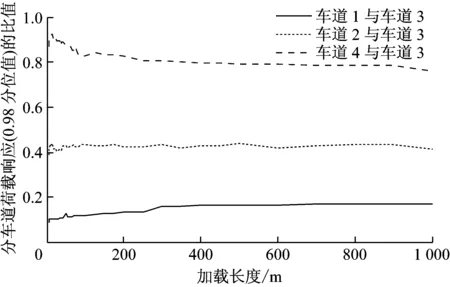
c 四车道图6 多车道中分车道荷载响应极值的比值与加载长度关系

Fig.6Changeruleofratioofextremelaneloadeffectalongwithloadinglengthinmulti-lanefreeway

在加载长度小于200 m时，REL具有一定的波动性，变化幅度较大，这是因为中小跨径桥梁荷载响应极值主要受重车及重车相遇控制[1,12]，根据表2和图3的分析，各车道上出现超载重车的概率不同且荷载水平有差别，因此在中小跨长范围内车道荷载响应比值存在较大波动.200 m以上加载长度、车道间荷载响应比值基本趋向稳定，这是由于大跨桥梁效应主要由车道内的平均荷载水平控制[12]，根据表2和图3的分析，多车道中分车道的车型和载重总体上是差别显著的.

根据趋于稳定段的REL，可知多车道中车道间荷载响应极值存在显著区别：①两车道中车道1仅为车道2的0.81倍；②三车道中车道3最显著，车道1与2分别为车道3的0.19倍和0.80倍；③四车道中车道3最显著，车道1、2、4分别是车道3的0.19、0.42、0.79倍.

分车道荷载响应极值的差别对于横向作用敏感的桥梁构件如横梁、多肋梁桥、宽幅桥等产生显著影响.这些差异说明不同车道数量下分车道的荷载响应极值水平不同，目前基于分车道极值荷载响应一致的假定与实际具有较大偏差[3]，且规范给出的多车道系数不能反映实测数据的特征.考虑到多车道系数与单车道模型配套使用，应该根据实测数据特点进行单车道模型的修正，并同时进行多车道系数取值的修正，以涵盖分车道的实际差异.

4 分车道荷载响应的损伤累积特性

疲劳是影响桥梁安全的另一关键问题，与强度安全主要受极值荷载响应不同，疲劳安全主要受荷载响应的损伤累积影响，即由应力幅值和频次所决定.分析随机车流作用下桥梁构件的疲劳安全问题，方法是：计算随机车流作用下的构件应力时程；采用雨流计数法获取应力幅频次曲线；通过Miner线性累积损伤准则(如式(2))计算等效应力幅，作为疲劳安全评估的基础.

(2)

式中：Δσi和ni分别为区间i的应力幅值及其频次；β是由疲劳试验确定的相关系数，这里取为3；Δσe是换算的常幅等效应力幅值.

基于第3节分析的5～1 000 m加载跨长的虚拟简支结构分车道跨中截面弯矩的荷载响应时程，研究随机车流作用下分车道疲劳损伤累积效应的差别.这里以跨中截面受拉主筋的疲劳为研究对象，把产生最大等效应力幅的车道作为基准，计算各加载长度下车道间等效应力幅的比值.同时，根据分车道交通流量的差异性，比较各车道下应力幅的历经频次.

图7通过盒图呈现了各加载长度下车道间等效应力幅的比值，盒型上、中、下分别为75%分位值(Q3)、中位值(Q2)、25%分位值(Q1)，上下界限分别为观测最大值和观测最小值.可知车道间等效应力幅比值变异性较小，这从盒型上下界|Q3-Q1|不超过0.05可以看出；盒图数据没有超限值，说明数据总体集中性较好，也说明了车道间等效应力幅比值的稳定性，这是由于车道间交通流量和荷载分布的差异是稳定的(如表2和图4)，因此损伤累积效应具有差别，且变异性小.结果显示：①两车道中车道1平均为车道2的0.79倍；②三车道中车道3最显著，车道1与2分别为车道3的0.24倍和0.76倍；③四车道中车道3最显著，车道1、2、4分别是车道3的0.24、0.46、0.88倍.这些结果与第3节分车道荷载响应极值的规律相同，但比值大小不一样，这是因为荷载响应损伤累积与极值是不同的问题.

分车道等效应力幅的平均日均频次(∑ni)比较显示：①两车道中车道1平均为车道2的0.95倍；②三车道中车道1与2分别为车道3的0.05倍和0.89倍；③四车道中车道1、2、4分别是车道3的0.26、0.38、0.68倍.

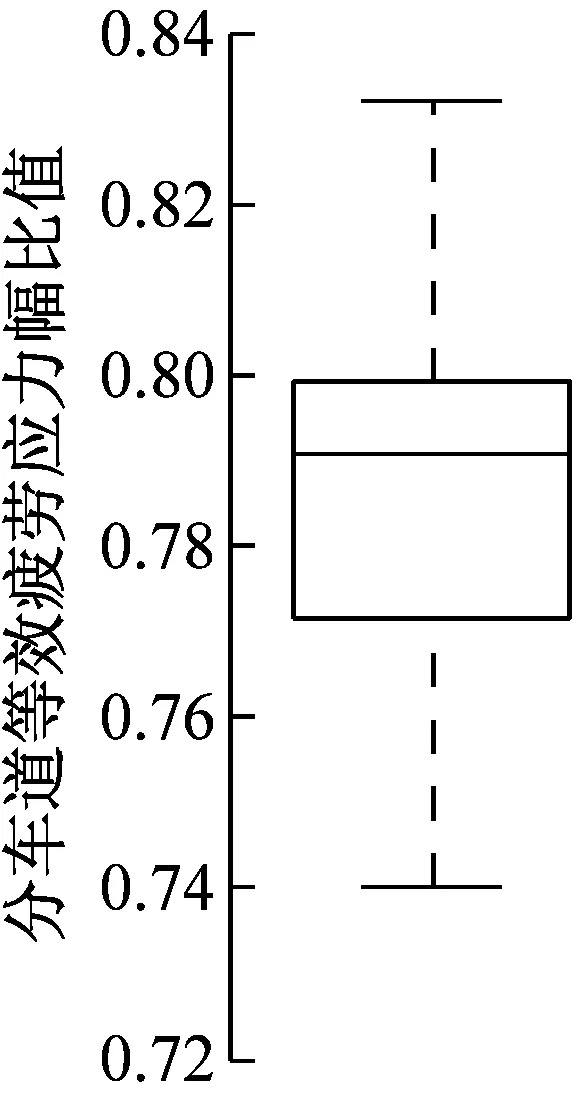
a 两车道的车道1与2

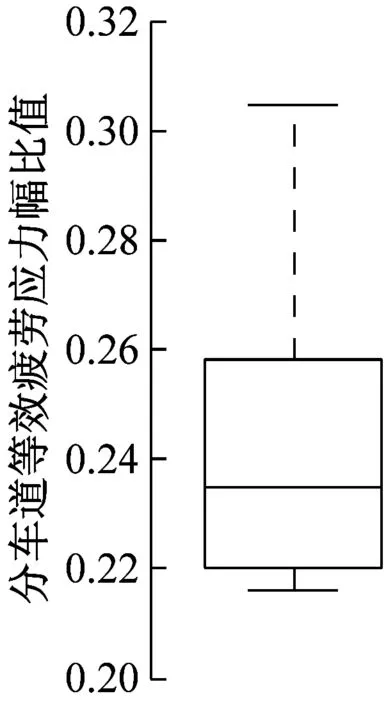
b 三车道的车道1与3

c 三车道的车道2与3

d 四车道的车道1与3

e 四车道的车道2与3

f 四车道的车道4与3图7 多车道中分车道等效应力幅比值Fig.7 Relative value of equivalent stress range of lateral lanes in multi-lane freeway

等效应力幅值和日均频次在分车道上的差别均说明内侧车道的疲劳损伤累积效应显著低于外侧车道，且车道数量越多差异越显著.车道间疲劳性能的差异说明进行桥梁抗疲劳设计中可以对快车道的构件进行优化，例如快车道的桥梁构件可以采取降低板件厚度或连接强度等措施，使其与慢车道的构件达到一致疲劳可靠度.同时说明用于桥梁疲劳设计的多车道系数取值应该与强度问题不同，且还需考虑分车道交通流量(等效应力幅频次)的差异.

5 结语

(1) 不同车道数量下各车型对车道具有特定的选择概率，使得分车道的车型组成、交通流量及荷载分布存在差异.

(2) 两车道中内外车道、三车道中外侧2个车道、四车道中外侧3个车道的外推车辆载重极值大体相当，说明这些车道的桥面结构局部设计可采用相同车辆荷载模型，而其他分车道应该考虑差异性进行修正或折减.

(3) 分车道荷载响应极值的比值不为1，说明分车道最不利荷载响应的水平不同，对于受横向作用敏感的桥梁构件可进行设计优化.

(4) 分车道的等效应力幅比值不为1，说明随机车流下分车道的损伤累积不同，针对该差别可进行优化，使得分车道构件的疲劳可靠度达到一致.

基于实测WIM数据展开研究，具有特定地点特征，但能反应我国多车道高速公路中分车道荷载作用的显著差别及规律.表明规范中多车道系数对于桥梁实际运营车辆荷载的表达存在出入，需要考虑分车道差异进行模型和数值的修正.

参考文献:

[1] 刘黎萍, 孙立军. 高速公路沥青路面轮迹横向分布研究[J]. 同济大学学报(自然科学版), 2005， 33(11):1449.

LIU Lipin, SUN Lijun. Research on wheel path lateral distribution for freeway asphalt pavements [J]. Journal of Tongji University (Natural Science), 2005, 33(11):1449.

[2] 阮欣, 周可攀, 周军勇. 某八车道高速公路车流特性及荷载响应[J]. 同济大学学报(自然科学版), 2015, 43(4): 555.

RUAN Xin, ZHOU Kepan, ZHOU Junyong. Vehicle flow characteristics and load effect of an eight-lane highway [J]. Journal of Tongji University (Natural Science), 2015, 43(4): 555.

[3] 鲍卫刚, 李杨海, 张士铎, 等. 公路桥梁车辆荷载纵横向折减系数研究[J]. 中国公路学报, 1995, 8(1): 80.

BAO Weigang, LI Yanghai, ZHANG Shiduo,etal. On the reduction coefficients of traffic loading laterally and longitudinally on bridges [J]. China Journal of Highway and Transport, 1995, 8(1): 80.

[4] NOWAK A S. Live load model for highway bridges [J]. Structural Safety, 1993, 13(1): 53.

[5] 宗周红, 李峰峰, 夏叶飞, 等. 基于 WIM 的新沂河大桥车辆荷载模型研究[J]. 桥梁建设, 2013, 43(5): 29.

ZONG Zhouhong, LI Fengfeng, XIA Yefei,etal. Study of vehicle load models for Xinyi River bridge based on WIM data [J]. Bridge Construction, 2013, 43(5): 29.

[6] 韩万水, 闫君媛, 武隽, 等. 基于长期监测的特重车交通荷载特性及动态过桥分析[J]. 中国公路学报, 2014, 27(2): 54.

HAN Wanshui, YAN Junyuan, WU Jun,etal. Extra-heavy truck load features and bridge dynamic response based on long-term traffic monitoring record [J]. China Journal of Highway and Transport, 2014, 27(2): 54.

[7] BLAB R, LITZKA J. Measurements of the lateral distribution of heavy vehicles and its effects on the design of road pavements[C]// Proceedings of the International Symposium on Heavy Vehicle Weights and Dimensions [S.l.]: Road Transport Technology, University of Michigan, 1995: 389-395.

[8] HUANG D, WANG T L, SHAHAWY M. Impact studies of multigirder concrete bridges [J]. Journal of Structural Engineering, 1993, 119(8): 2387.

[9] ENRIGHT B, O'BRIEN E J. Monte Carlo simulation of extreme traffic loading on short and medium span bridges [J]. Structure and Infrastructure Engineering, 2013, 9(12): 1267.

[10] ZHOU X Y, TREACY M, SCHMIDT F,etal. Effect on bridge load effects of vehicle transverse in-lane position: A case study [J]. Journal of Bridge Engineering, 2015, 20(12): 04015020.

[11] 北京替帝西交通科技有限公司. TDXWIN高速公路车辆动态称重系统说明书[M].北京: 北京替帝西交通科技有限公司, 2014.

Beijing TDX Traffic Science and Technology Co. Ltd. Instructions for TDXWIN highway traffic load weigh-in-motion system [M]. Beijing: Beijing TDX Traffic Science and Technology Co. Ltd., 2014.

[12] 阮欣, 周军勇, 石雪飞. 桥梁汽车荷载响应极值外推方法综述[J]. 同济大学学报(自然科学版), 2015, 43(9): 1339.

RUAN Xin, ZHOU Junyong, SHI Xuefei. Review on extreme extrapolation methods of bridge traffic load response [J]. Journal of Tongji University (Natural Science), 2015, 43(9): 1339.

[13] BUCKLAND P G, MCBRYDE J P, ZIDEK J V,etal. Proposed vehicle loading of long-span bridges [J]. Journal of the Structural Division, 1980, 106(4): 915.