从默会性认识走向显性化结构

钱建兵

【摘 要】日常生活经验促使学生形成了“日常数学概念”，而在这些“日常数学概念”中，存在着个人的、生活化的、零散的对数学概念的理解与认识，教学中要了解并利用“日常数学概念”中科学的、数学化的成分，引导学生在操作与思考的不断深入与精致中，凸显数学概念的关键，并认识到原有知识中的不足，由模糊走向清晰，祛除非本質属性并进行抽象概括，促进显性化数学知识结构的形成。

【关键词】默会性；显性化结构；经验；思维

一、教材与学情分析

苏教版教材中“平行四边形的认识”是在三角形的认识之后编排的内容。教材在编排这一内容时，让学生利用方格纸，画出一个平行四边形，从而发现平行四边形的特征。这样的编排，有利于学生充分利用原有认知平行四边形的经验。

教材内容如下图：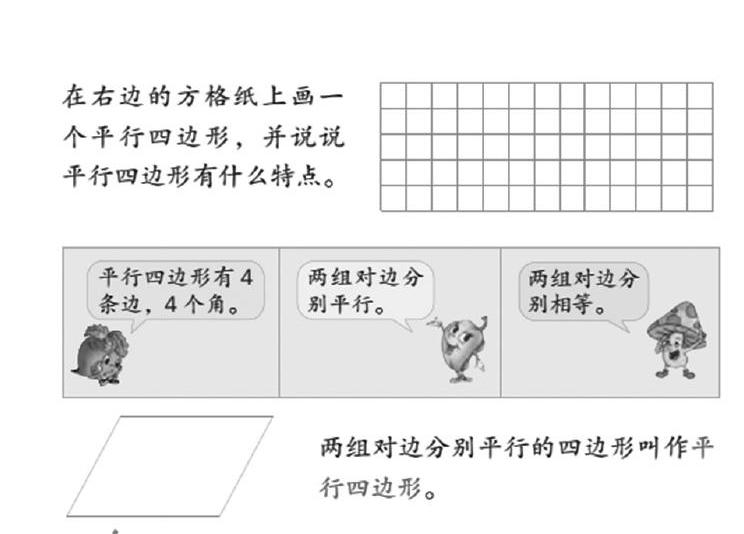

学生在生活中见过、接触过大量的平行四边形，在图形的认识过程中，也建立了平行四边形的“标准式”：上下一组对边平行、相等，并伴随着一些直觉性的认识，如有两个锐角和两个钝角。因此，本课的教学，需要帮助学生排除生活概念的干扰，理清哪些是平行四边形本质的特性，哪些是平行四边形非本质的特性。在此探究的过程中，积累学习平面图形的经验，发展学生的空间观念。方格中的平行线、单位长度，正好利于学生发现平行四边形的特征，但也应注意到，这种加工好的素材，也可能会限制学生的思考空间。

与原教材提供多种思路作（画）平行四边形相比，只提供一种材料（思路），是向真实儿童经验的回归。原教材中的一些方法只是成人想出的，并不是学生根据自己的经验想出来的。这也提醒我们，成人提供的经验是否能与儿童的经验产生联结，是这种方法有无教学意义的依据。而让学生在方格纸上画平行四边形，学生容易将经验中的平行四边形、平行线的认识与方格纸上的条件联系起来，产生一种联结，学生在这一情境中更容易整体感知平行四边形的特征。

课前的调查表明，学生在脑中有着标准的平行四边形的表象，能认识、判断一个图形是不是平行四边形。如学习长方形与正方形的认识一样，在课堂学习之前，大量的社会性的、缄默的学习，使学生已经建立了相关的认识。但这种认识是整体性的，这种认识是一种默会性认识，处于一种“不能言”的状态，因而是不成形的、无结构的。既然已认识了平行四边形，那么再让学生去经历所谓的猜想、操作、验证，必定索然无味，学生的思维就会始终处在一个比较浅的应对层次上面。另外，对平行四边形特征的认识，学生对平行的感知要强于对长度特征的感知，特别是如何引导学生去发现标准式中左右一组对边平行关系，进而发现对边的相等关系，从而形成明确的结构化的认识，这是教学中需要思考的问题。

二、教学过程

基于以上的认识与思考，我进行了以下的教学实践。

（一）引入

谈话：四根小棒，可能围成一个什么图形？

生：长方形。

师：能围成一个长方形吗？（给出四根都不一样长的小棒）

生：不能。四根小棒要两根两根一样长，因为长方形的对边相等。

师：除了对边相等，长方形还有什么特征？

生：四个角都是直角。

师：看来，我们研究一个图形可以从边与角这两方面去描述一个图形的特征。这四根小棒只能围成长方形吗？

生：还可以斜过来，围成平行四边形。

师：今天我们就来认识平行四边形。

【反思】回顾长方形的特征，唤起已有平面图形的学习经验。同样的四根小棒，既可围成长方形，也可围成平行四边形，说明学生对对边相等有一定的认识，只是在教学中我们需要将这些特征显性化和系统化，将其纳入平行四边形的特征系统。

（二）研究特征

1.呈现“标准式”，反思中初现边的特征

师：你能在方格纸上画一个平行四边形吗？画好了在小组里交流一下。（学生在作业纸上操作）

集体交流。

生：我画的时候先画出一组边（指水平方向的），再画出另一组边（指左右方向的）。

生：也可以这样竖着画。

师：老师注意到了，不管是先画上下一组边还是先画左右一组边，都要正好画在这些格子的边线上。

生：因为方格纸上横着的线都互相平行，竖着的也互相平行。

师：你们的意思是说平行四边形有什么特点？

生：这两条边是平行的。

【反思】借助方格纸，让学生将原有认识中的平行四边形的“标准式”呈现出来，并借助这一“标准式”，来进一步认识平行四边形的特征。学习的社会性告诉我们，人的社会性本质所驱动的学习都是基于有意识和无意识的模仿。小组的学习形式让不同质的学生有效地进行交互，促使每一个个体原有经验的激活。学生对平行四边形的原有认识具有整体性，能从整体外观上判断一个图形是“像”还是“不像”平行四边形。即便有学生在画的时候把两边画得不一样长，但在自己的观察之后，能及时地改正过来，并认识到自己错误的原因。这也充分说明他内心不断地将所画与平行四边形的标准式表象进行比较。因此，这里画平行四边形是对特征的整体呈现。教学中，要让学生充分地画，并让其充分地进行自我反思与同伴交流，即与心里表象不断对质。这是默会认识走向显性的前提。但此时学生对平行四边形缺少精确的把握，即特征的明确。弗赖登塔尔说过，只要学生没能对自己的活动进行反思，他就达不到高一级的层次。引导学生对画法的反思，即对平行四边形的认识走向了显性化的第一步。

2.思维聚焦，明晰特征

师：我们已会在方格纸上画平行四边形，下面两条直线，你能利用它们，画一个平行四边形吗？

出示：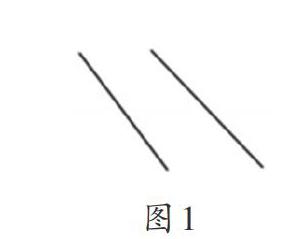

生：不能，因为这两条直线不平行。

师：它能成为两组对边中的任意一组吗？

生：不能。平行四边形的两组对边分别平行。

师：你是怎么知道平行四边形的两组对边分别平行的？拿出刚才画的平行四边形，你准备怎么检验？

生：我们画的时候，一组对边就正好是方格的边线，另一组虽然不在边线上，但是都一样地斜过去，角度一样，所以我判断是平行的。

生：但也不能代表它们一定平行。我觉得可以用画平行线的方法检查一下。

生：可以看成是这边上的一个三角形平移过去，那么平移后的对应边应该是平行的。

师：想象一下，怎样调整，就能成为平行四边形？调整之后的平行四边形是什么样子的？

师：（出示第2组）能利用它们画一个平行四边形吗？

生：也不能，长度不相等。

生：可以，虽然现在看上去它们不等，但可以延长其中的一条，使两条一样长。

师：你们的意思是说平行四边形的对边还要相等？你能验证吗？

生：我是数的（指方格纸上的平行四边形）。上下两条边一样，左右两条边也一样。

师：左右两边也能数吗？

生：可以量。

生：它们都是同样大的长方形对角的连线。

生：我还是平移的，平移后对应边长度相等。

师：想象一下，怎样使它们成为平行四边形的一组对边？想一想这个平行四边形的样子。

小结：平行四边形的特征；变式判断。

【反思】通过这个层次的操作，将学生的思维引向精致化的过程，从关注整体感觉到局部特征，帮助学生超越经验。学习新知的过程，是与标准比较的过程。因为学生已认识平行四边形，这两个没有完成的图形，分别指向了平行与相等的特征，引导学生将自己的经验与平行四边形的特征进行对比，从而引导学生重新发现特征。这里的验证，是学生为了对自己直觉经验的一种确定，因此具有自主性，不是让学生在教师的指挥下进行的“验证”。正因为如此，学生能积极地思维，能够激活已有的经验与画平行四边形时的体验。特别是对于对边相等，不正好画格子线上，能进行简单的推理。这种思维方式正是在小学需要适时培养的。不少学生在高年级，仍依赖“眼见为实”的直观思维思考问题，图形看上去是直角，就认为是直角，线段之间的长度看见是什么关系就认为是什么关系，思维缺少严谨性。不给出完整的图形，而是讓学生想象，是需要加工的“半成品”，这样的发现就有一种思维上的探究，在尝试、想象的过程中强化的平行四边形的表象，对边的特征有了新的认识，发展了空间想象力。

（三）研究高

出示标准式平行四边形，你能根据对三角形高的理解说说什么是平行四边形的高吗？

生：这一组对边之间的距离就是它的高。

师：画一条它的高。想一想可以画几条？它们的长度相等吗？

生：这一组对边上的高有无数条，长度都相等。

出示高的定义：像这样从平行四边形一条边上的一点到它对边的垂直线段，是平行四边形的高，这条对边是平行四边形的底。高用虚线，并且及时画上垂直记号。

师：另一组对边可以画高吗？这样的高可以画多少条？跟另一组对边上的高一样吗？

生：可以。

师：原来平行四边形两组对边间都可以画高。

师：角顶点上的一点。这一点可以怎么画高？有不同的画法吗。为什么这一点可以画两条不同的高？

三、教学反思

（一）对比反思中将经验的、模糊的认识显性化

学生的已有认识是一切教学的起点。正是对起点有了比较准确的判断，对于特征的认识，没有费多少周折，让学生自己去探索、发现。重点是通过学生的反思内省，达到对特征的认识由模糊走向清晰，由缄默走向显性，由零散走向结构。在这些过程中，让学生的思维参与到课堂中，注重的是空间想象，而不是不假思索地动手。比如对对边相等的再确定，学生能够沉静在思考中，进行论证推理。其实，有时候教学被教师复杂化反而让学生不知所措，学生真正用于思考的时间很少。特征的发现过程，没有多少花哨的活动，只是不断地引导学生与所画的标准式进行对比，从而发现熟悉地方的风景。

（二）提供的材料要能够让学生突破原有的朴素认识，聚焦概念本质

在课上讨论平行四边形与长方形的关系时，不少学生一致认为长方形不具备平行四边形的特征，理由是长方形四个角是直角，而平行四边形的四个角是两个锐角与两个钝角。这使笔者深刻地意识到学生对平行四边形原有的认识：学生原先认识的平行四边形的特征，不仅有边的，更有角的。因为原有的认识图形特征（长方形、正方形）的经验就有对角的关注。两个钝角和两个锐角，这是学生对平行四边形朴素的认识，因为这一“特征”比较外显、直观，而且掩盖、干扰了对实质——对角相等的认识。虽然教材没有提及，但这确实是学生会提及的真的数学问题，我们无法也不能回避。这个问题不解决，学生难以理解平行四边形与长方形的关系就很正常。因为他们看到的平行四边形的角确实是这样的，且这样的观念根深蒂固。如果认识了平行四边形，学生对角的认识还是原有认识，这样的知识结构是有缺陷的。从知识的获取方面来说，让学生不限于一种方式（边的特征）定义，多视角认识概念，有利于形成“概念域”，是概念学习过程中深层次的精致。直面学生的各种真问题进行教学，是儿童立场的根本。因此，提供的材料要能够让学生突破原有的对平行四边形角的朴素认识，聚焦概念本质。

教学研究就是这样，就是不断地发现问题、解决问题而后又发现新问题、解决新问题的过程。如果利用两个完全一样的三角形拼一个平行四边形，一方面，可以感知对边相等，另一方面，主要是为学生研究平行四边形的角的特征提供一个平台，同时丰富图形转化的经验，为三角形的面积计算公式推导做好铺垫。在交流时，明确问题：四个角有什么关系，而不是模棱两可“角有什么特征”，学生就自然而然地表达为“对角相等”。因为在操作时，他们是能发现平行四边形的一组对角是两个三角形的对应的一个内角，而另一组则是由三角形另外两个角拼成的，并且是相等的。这样就可能没有说教，让学生自觉地放弃了“两个钝角、两个锐角”的直觉经验，从而上升到特征的认识，理解平行四边形与长方形的关系时也就没有什么障碍了。

（江苏省南通市通州区西亭小学 226301）