基于集对分析的城市供水管网漏损预测及降漏研究

赵明宪，饶碧玉，王静

(云南农业大学建筑工程学院，云南 昆明 650201)

集对分析(set pair analysis)理论是一种处理不确定性系统因素的数学工具，能够有效地处理和分析一些不确定、不完整的信息，并从中找出事物发展的潜在规律和趋势[1]。集对分析理论在预测分析方面已经较成功地应用到许多领域，王红芳等[2]运用集对分析方法对长江水系中几个重要的水文站年径流量进行了预测，预测合格率较高，验证了集对原理在水系年径流的预测模型的可靠性；张明等[3]通过建立集对分析管网漏损预测模型(SPA-LF)对供水管网的漏损数量和漏损频率作了预测分析，并对预测结果作了有效性分析。城市供水管网渗漏不仅浪费了大量的水资源，影响供水的安全性与可靠性，还会造成管道基础的损坏，破坏供水管网及其他地下公用设施[4]。掌握供水管网漏失情况是漏损管控的基础，同时也是管网维护和后续管道优先更新改造判定的依据。由于供水管网的管材在实际运行管理过程中受多种因素的交互影响，同时管道的漏损情况存在较大的不确定性，集对分析理论为解决不确定性问题研究提供了新的途径与方法。本文以云南省某城市典型供水片区为例，运用集对分析漏损预测模型(SPA-LF模型)分析其历史漏损数据，预测未来不同管材的漏损趋势，对提高供水企业主动检漏水平与供水安全可靠性、降低管网漏损率与供水成本具有重要的现实意义。

2 供水片区现状

截至2016年，选取的云南省某城市典型供水片区供水管网约413 km，2016年平均日供水量约1.46×104m3，服务面积406 km2，服务人口36.5万人。各类型管材情况：灰口铸铁管占9.01%，球墨铸铁管占70.97%，钢管占9.56%，PE管占4.36%，水泥管占3.70%，其余管材(主要有玻璃钢夹砂管、钢塑复合管等)占2.40%(见表1)；供水管网管径选用DN15～DN1200，其中选用的DN100占13.83%，DN150占14.48%，DN200占12.74%，DN300占22.35%，DN400占14.07%，DN500占7.82%，DN600占5.42%，DN800占3.95%，其余管径占5.35%。

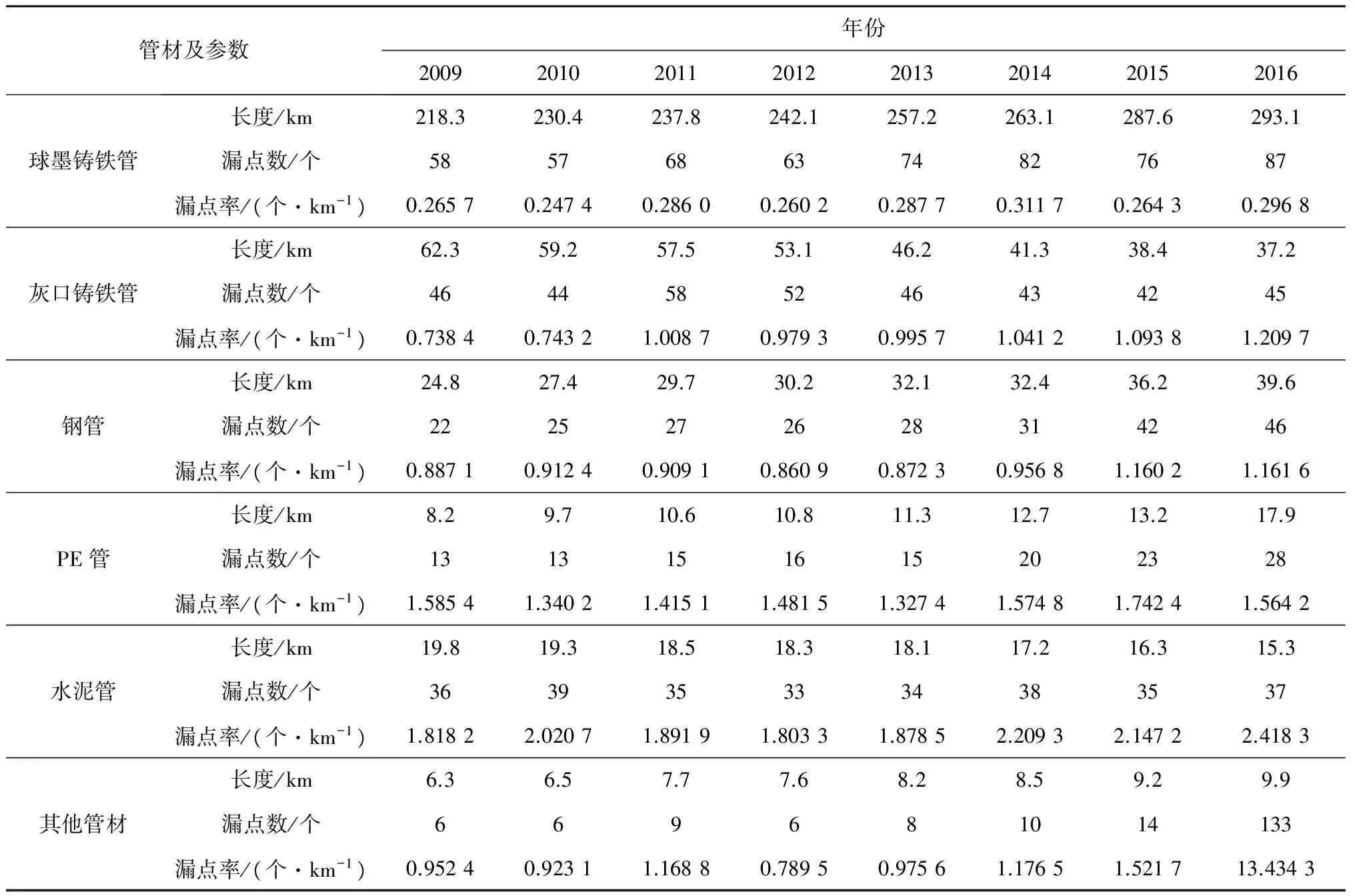
表1 2009—2016年某供水片区供水管材长度及漏损情况统计表Table 1 Statistics table of the length of water supply pipe and its leakage situation for a water supply area from 2009 to 2016

3 SPA-LF模型构建与预测分析

3.1 SPA-LF模型构建

(1)由于资料有限，将2009—2016年的漏损资料作为历史样本数K中的影响因子xi(i=1,2,3,…,n)，集合Bi(xi,xi+1,xi+2)(i+2≤n)作为影响因子集，采用均值离差法计算各影响因子的平均值uj和平均绝对离差dj(j=1，2，…，n)。根据(0，uj-0.5dj]、(uj-0.5dj，uj+0.5dj)、[uj+0.5dj，+∞)将各影响因子分为Ⅰ、Ⅱ和Ⅲ类。

(2)把2017年漏损量x9的主要影响因子集B7与历史样本的漏损量xi的主要影响因子集Bi建立集对H(Bi+1，Bi)(i=1,2,3,…,n-2)，根据集对分析原理，计算H(Bi+1，Bi)的同异反联系度：

(1)

式中，N为集合特性的总项数；S为同一性的个数；P为对立性的个数；F为差异性的个数；i为差异不确定系数，在(-1,1)区间取值，有时仅起差异标记作用；j为对立系数，一般j=-1，有时仅起对立标记作用。

式(1)可简化为：

U=Ai+BiI+CiJ，

(2)

式中，A为同一度，A=S/N；B为差异度，B=F/N；C为对立度，C=P/N。

式(2)中A、B和C分别为H(Bi，B1)的同一性、差异性和对立性，Ai、Bi和Ci分别为集对H(Bi，B1)中同一性个数、差异性个数和对立性个数的归一化值[5]。

将I和J取值后，联系度U变成了联系数U′。若Bi+1与Bi间的差异性越大，则U越接近于-1，表示这两因子集越倾向于不相似性；若这两因子集间的差异性越小，则U越接近于1，表示这两因子集越倾向于相似性[6]。于是，联系数U'就是可变模糊集Bi+1与Bi间的相似性的一种相对差异度函数，故该模糊集的相对隶属度函数可写为：

(3)

(3)根据预测年的影响因子与漏损量历史样本的影响因子之间的相似性，可建立漏损量变化的预测模型：

(4)

式中wi即为最相似的历史样本的漏损量xi的权重；i=k1，k2，…，kK为K个与预测当前年漏损量xi+1的主要影响因子集Bi+1最相似的历史样本的序号[3]。

3.2 预测分析

通过对该供水片区内的管网漏损资料的归类与分析，运用SPA-LF模型进行管网漏损情况的预测。一方面从供水管材的漏点数的角度进行预测分析，将每年的漏点数作为预测模型的影响因子，可以预测分析出未来不同管材类型漏损的数量趋势；另一方面从管材的漏点率(个/km)的角度进行预测分析，将不同管材每年求得的漏点率作为预测模型的影响因子，相比漏点数量而言，漏点率的趋势预测能够更好地从宏观上反映出管网的漏失水平及漏损的总体情况，从而便于采取针对性的漏损控制措施。

2009—2016年间云南省某城市典型供水片区所选用管材中球墨铸铁管数量占比最大，因此参照模型构建的计算步骤以球墨铸铁管为例进行2017年度管网漏点数和漏点率的预测分析，其他管材预测步骤和方法相同。

3.2.1 管网漏点数预测分析

(1)将2009—2016年(n=8)球墨铸铁管漏点数作为影响因子并构建影响因子集Bi(i=1,2,3,…,6)，然后采用均值离差法对构建的影响因子集进行求解计算，结果见表2。

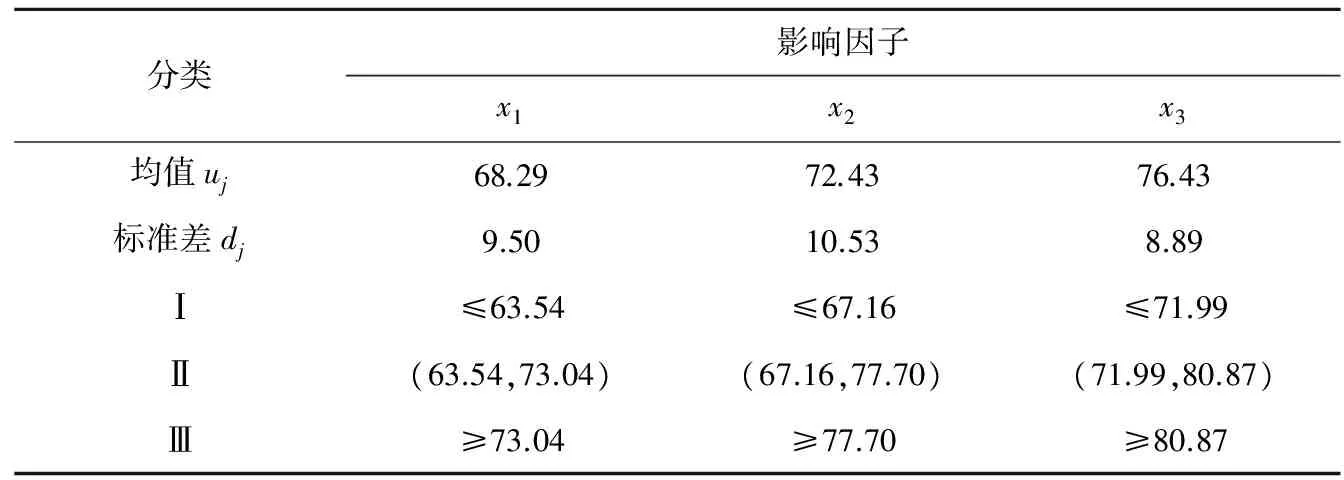
表2 漏点数集合分类及计算结果Table 2 Classification of leakage quantities set and its calculation results

(2)构建当前集合B7=(76，87，85)，根据分类标准符号量化为B7=(Ⅲ，Ⅲ，Ⅲ)。构造集对H(B7，Bi)(i=1,2,…,6)，计算各集对的联系度，并取I=0.5和J=-1，得到集对H(B7，Bi)(i=1,2,…,6)的联系数U′，结果见表3。

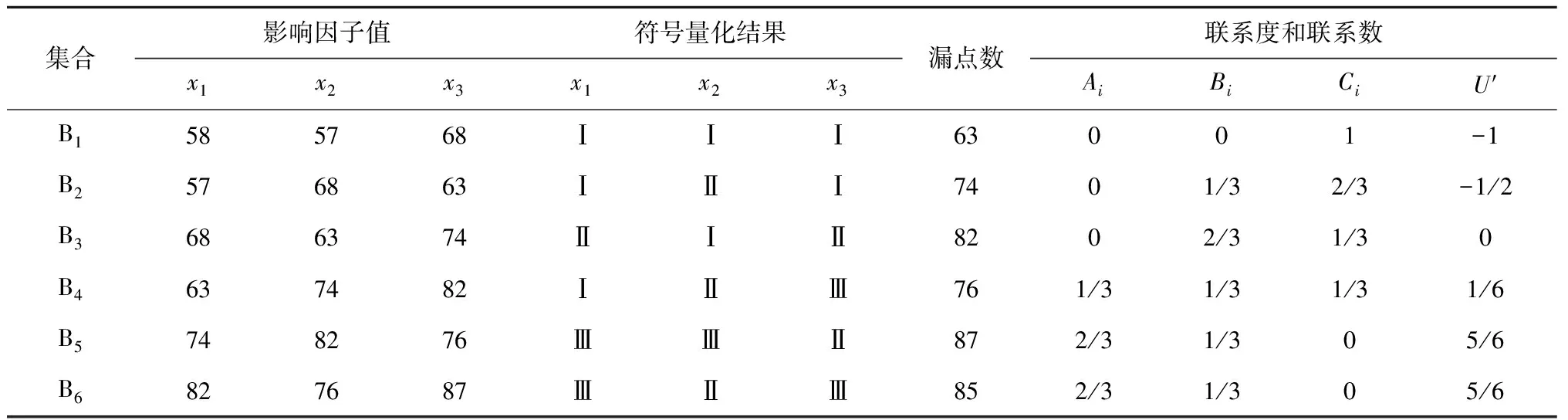
表3 漏点数预测集合Bi符号量化结果和联系度(数)Table 3 Symbol quantitative results and connection degree (number) of leakage quantities forecasting set Bi

(3)根据较大联系数U′个数的具体情况，选择K=2进行2017年度球墨铸铁管漏损预测。此时，较大联系数的历史样本分别为B5和B6，即用2015年及2016年的实际漏点数76和87，根据式(4)加权计算得到2017年的漏点数预测值为81.5。

(4)其他管材漏点数预测分析

参照上述模型预测分析方法，以2009—2016年某供水片区数据(见表1)作为预测分析基础，灰口铸铁管、钢管、PE管、水泥管和其他管材2017年度管网漏点数预测结果见表4。

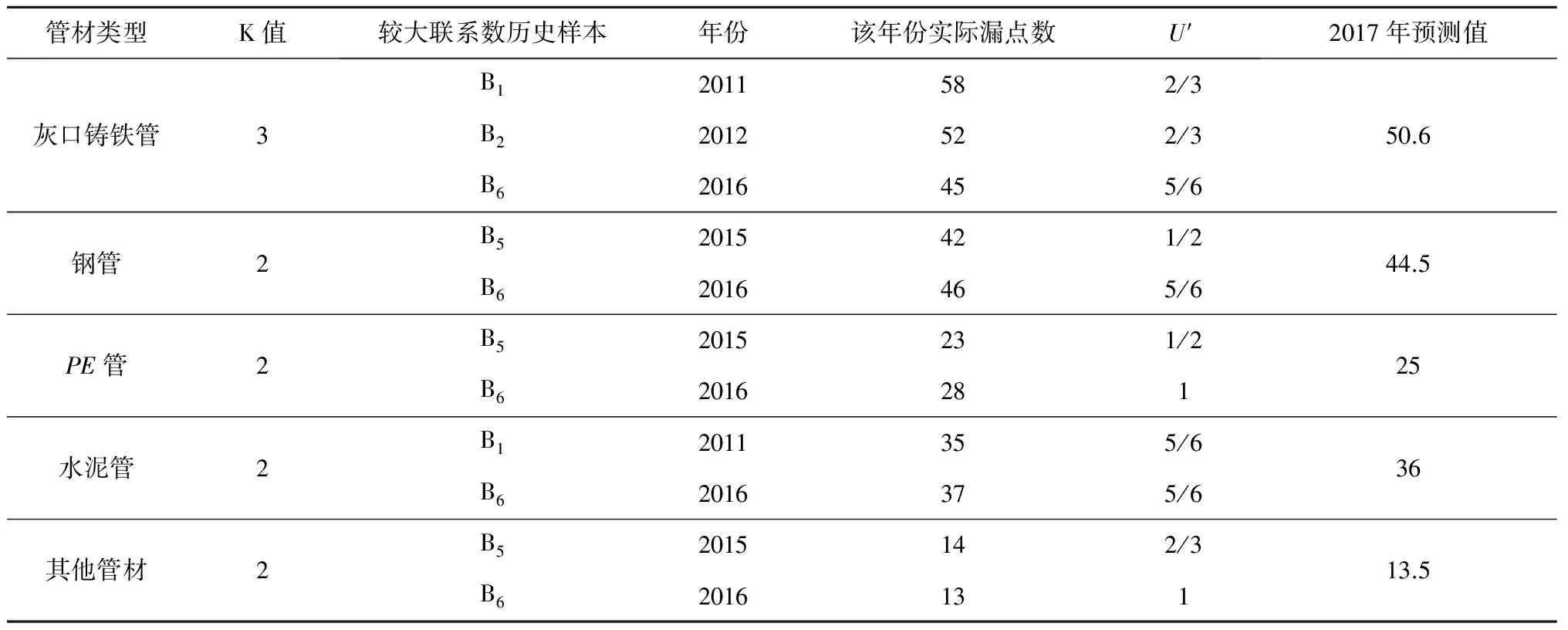
表4 某供水片区管网2017年度漏点数预测统计表

(5)结果分析

通过对不同材质管网漏点数的预测结果发现，球墨铸铁管和灰口铸铁管的漏点数较多，其次是钢管和水泥管，漏点数相对较少的是PE管和其他管材，在下一年度的供水管网运行管理中应重点加强对球墨铸铁管和灰口铸铁管的漏损检测管理，同时对漏损情况较严重的其他管材也应采取必要的主动检漏措施。

3.2.2 漏点率预测分析

(1)将2009—2016年(n=8)球墨铸铁管漏点率作为影响因子构建影响因子集Bi(i=1,2,3,…,6)，然后采用均值离差法对构建的影响因子集进行求解计算，结果见表5。

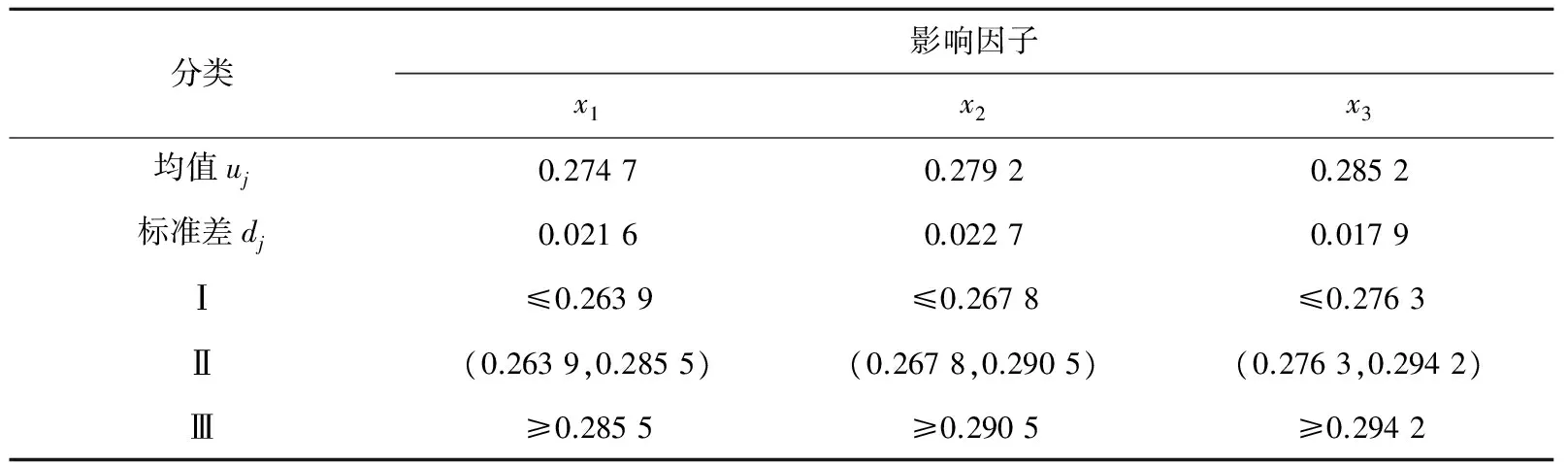
表5 漏点率集合分类及计算结果Table 5 The classification and calculation results of leakage rate set

(2)构建当前集合B7=(0.264 3，0.296 8，0.290 0)，根据分类标准符号量化为B7=(Ⅱ，Ⅲ，Ⅱ)。构造集对H(B7，Bi)(i=1,2,…,6)，计算各集对的联系度，并取I=0.5和J=-1，得到集对H(B7，Bi)(i=1,2,…,6)的联系数U′，结果见表6。

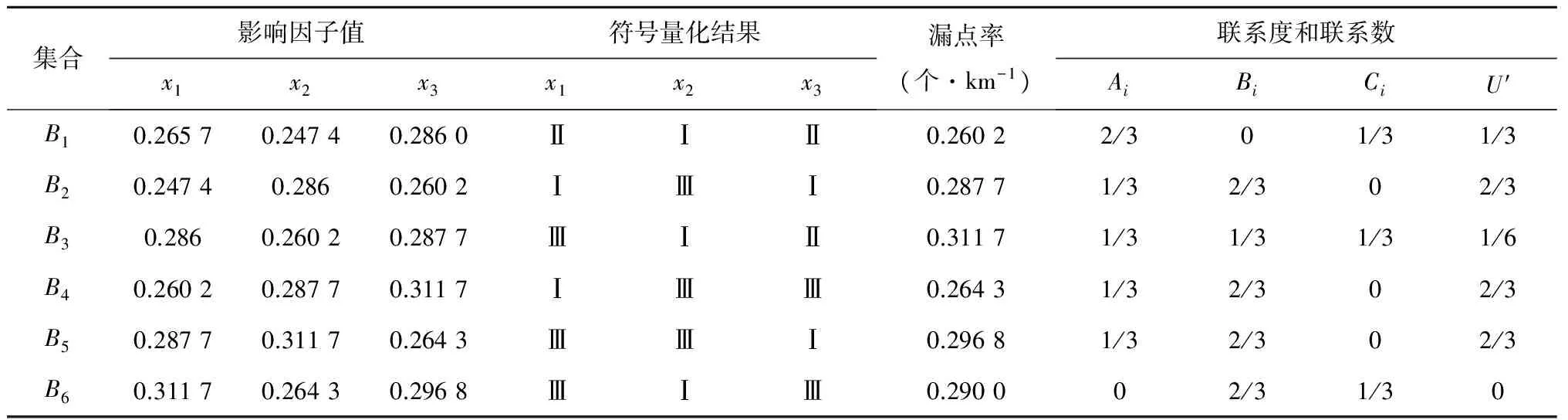
表6 漏点率预测集合Bi符号量化结果和联系度(数)Table 6 Symbol quantitative results and connection degree (number) of leakage rate prediction set Bi

(3)根据较大联系数U′个数的具体情况，选择K=3进行2017年度球墨铸铁管漏点率预测。此时，较大联系数的历史样本分别为B2、B4和B5，即用2012年、2014及2015年的实际漏点率0.260 2、0.311 7和0.264 3 个/km，根据式(4)加权计算得到2017年球墨铸铁管漏点率预测值为0.278 7个/km。

(4)其他管材单位管长漏点率预测分析

参照上述模型预测分析方法，以2009—2016年某供水片区数据(表1)作为预测分析基础，灰口铸铁管、钢管、PE管、水泥管和其他管材2017年度管网单位管长漏点数预测结果见表7。

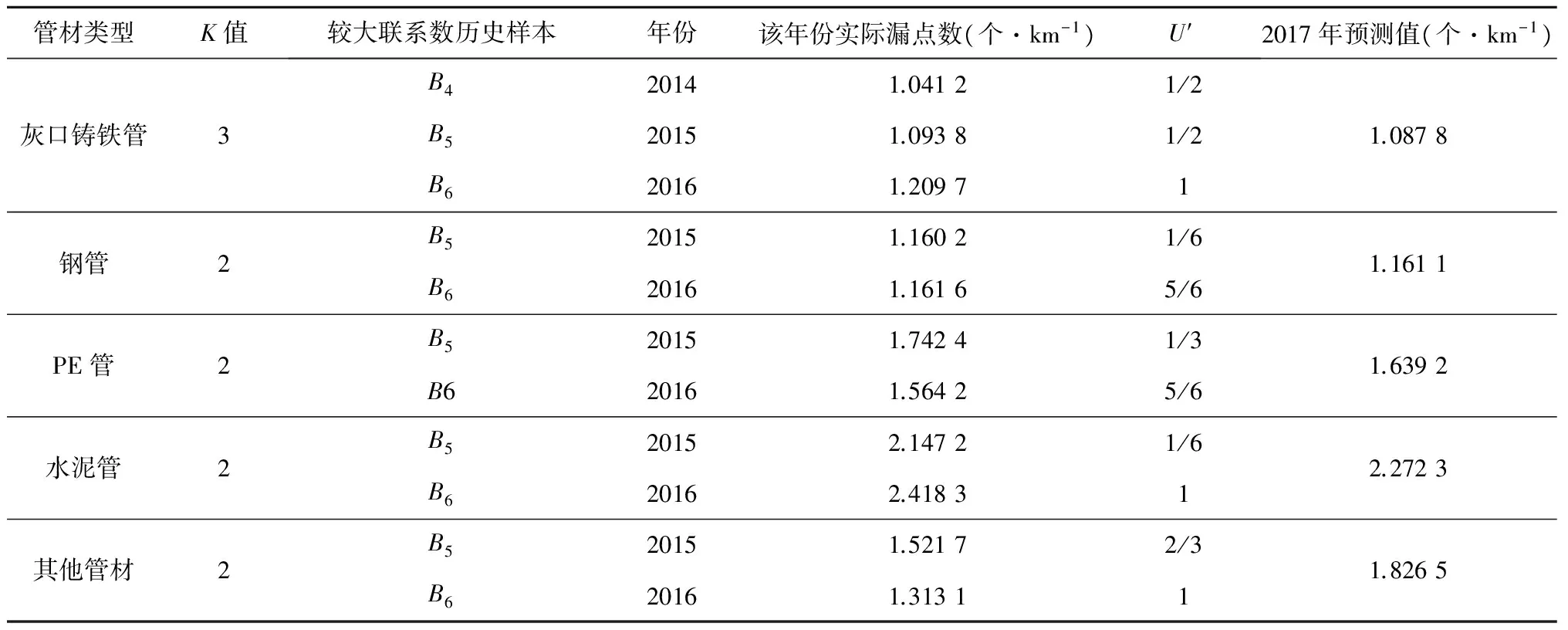
表7 某供水片区管网2017年度漏点率预测统计表Table 7 Prediction chart of leakage rate in 2017 for a water supply area pipe network

(5)结果分析

通过对不同材质管网的漏点率的预测结果发现，与漏点数相比，漏点率能够更好地反映出管材单位长度上漏损的数量多少与漏损的严重程度，水泥管由于管龄较长漏损情况比较严重；PE管受水压、温度等因素影响接口处或转弯处容易引起管道爆管现象，而且管道漏损相对严重；钢管、灰口铸铁管使用时间过长容易引起管道内部结垢从而造成管道漏损；球墨铸铁管漏损情况相对较好，但在该研究区域内球墨铸铁管占比较大，其漏损问题同样不能忽视。

4 降漏措施

运用SPA-LF模型，对2009—2016年云南省某城市典型供水片区管网漏损数量进行预测分析，结果表明水泥管、PE管、普通钢管、灰口铸铁管和其他管材的漏损情况较严重，应该重点加强这部分管材的检漏频次和有计划有步骤地对老旧管网进行更新改造工作。根据管网漏损预测分析结果，现提出以下几点针对性的降漏措施：

(1)提高主动检漏水平

通过对2017年供水管网漏损情况的预测分析，针对不同管材的漏损数量多少情况，应针对性地加强主动检漏管理，提高主动检漏水平。主动检漏不仅可以避免或减少管道漏损情况，还可以提前对发生轻微漏损情况的管道进行检修，避免更大程度漏损现象的发生。

(2)加大管网更新改造力度

针对水泥管等管材漏损严重的实际情况，应加强该部分管材的更新改造力度，消除安全隐患，降低管网漏损水平。同时在进行新工艺、新技术和新材料对比选择时应综合考虑管径、输水压力、管道接口形式、管道承受的外部压力及管道内可能遭受的腐蚀等各因素影响，合理选材[7]。有计划有步骤地进行城市供水管网的更新与改造，对改善管网运行状况、保障用水的安全可靠性和降低管网漏失水平具有重要作用。

(3)积极推广和应用非开挖修复技术

在进行管网更新改造时，为避免和减少施工过程中对地面交通、建筑物基础和周围环境的干扰，降低对正常的生活秩序影响，建议推广和应用非开挖修复技术(在不开挖或者少量开挖的前提下对敷设于地表下的管线、管道等进行铺设、更换、维修和探测的一种特殊的地下施工技术[8])进行管道的施工铺设工作，其常用的方法有水平导向钻进法、盾构法、滑动内插法和原位固化法等。

5 结语

本文通过运用SPA-LF模型，以2009—2016年云南省某城市典型供水片区管网漏损数据为基础，从供水管网漏点数和漏点率两个方面分析了该供水片区不同类型管材目前的实际漏损情况，并预测出2017年度不同类型管材的漏点数和漏点率。针对未来可能出现的管网漏损情况和管网漏损趋势提出了三方面的降漏措施，从而实现逐年管网漏损控制目标，达到整体降低管网漏损率的目的。

参考文献：

[1]蒋云良,徐从富.集对分析理论及其应用研究进展[J].计算机科学,2006(1):205-209.

[2]王红芳.集对分析在水文水资源中的应用研究[D].成都:四川大学,2008.

[3]张明,李鹏,周润娟.基于集对分析的供水管网漏损预测模型[J].供水技术,2012,6(3):28-31.

[4]王立伟,万珊,姚宗玉.给水管网漏损预测模型研究[J].黑龙江水利科技,2008,36(6):58-60.

[5]赵克勤.集对分析及其初步应用[M].杭州:浙江科学技术出版社,2000.

[6]金菊良,魏一鸣,王文圣.基于集对分析的水资源变化趋势的相似预测模型[J].水力发电学报,2009,28(1):72-77.

[7]金伟如.城市供水管网漏水原因分析及应对措施探讨[J].给水排水,2015,41(增刊):359-361.

[8]张浩.非开挖技术在城市给排水管道施工中的应用[J].安装,2009(9):27-29.