基于预处理的点到点最短路径计算方法
2018-05-03陆文琦谷远利李萌王硕张源
陆文琦,谷远利,李萌,王硕,张源
(北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京 100044)
随着计算机和地理信息技术的快速发展,智能导航与位置查询服务在辅助人们出行方面发挥出越来越重要的作用,尤其是车载导航系统正逐渐成为所有驾驶人员的必备产品。但是由于城市汽车保有量的不断攀升,道路网络规模不断增大,交通情况愈发复杂,用户急需更加高效、准确的最短路径算法以获取动态灵活的导航服务。
最短路径算法被广泛应用于车辆诱导、交通流分配等领域,最早用来解决点到点最短路径的算法是经典Dijkstra算法[1],Bellman-Ford算法和Floyd算法也被用来解决过此类问题。Hart等[2-3]在经典Dijkstra算法基础上提出了A*算法,该算法利用当前点到目标点的最短路径长度的估值更快地向目标点靠近,始终根据既定的规则,通过不断扩大“最有希望”[4]的节点集合进行探索,由于在搜索过程中省略大量无谓的搜索路径,比Dijkstra算法的效率更高。与A*算法类似,Pearl等[5]提出了Weight A*算法(简称WA*),在计算路径时,A*算法和WA*算法均以两点间直线距离作为最短路径长度估值,WA*求解得到的路径质量与其算法运行时设置的参数有关,可以在大规模网络上找到一条与标准最短路径相差不大的路径。
以上算法主要以标号法为主,没有对图进行预处理。针对大规模网络计算时间长、占用内存空间大、无法应对快速查询的缺陷,在传统算法的基础上逐步形成了基于预处理的最短路径算法,包括预处理阶段和路径查询阶段[4]。例如,在A*算法的基础上,Goldberg等[6]提出了基于预处理的ALT算法,由A*、Landmark和Triangle inequality方法组合而成。此外,与经典单向Dijkstra算法相对应,双向Dijkstra算法可以以源点和终点为圆心同时向外搜索,加快了搜索效率,并且双向算法可以与其他方法相结合形成新的算法,解决点到点最短路径问题。Goldberg等[7]将双向算法和A*算法、ALT算法结合,并且通过添加快捷弧的预处理方法,使查询效率极大提升。其他常用的预处理方法有层次化法,包括分割法[8]、层次公路HH算法[9]、HNR算法[10]、THR算法[11]等等。
本文在reach剪枝算法的基础上,详细介绍了reach的计算方法,包括reach精确值和上界值,对两种reach计算方法在不同规模路网上进行对比,并将基于reach的剪枝算法与双向Dijkstra算法结合形成了RE算法,利用EFSS数据结构[12-13]建立了包含路段阻抗和交叉口转向延误的交通路网,通过算例和几种不同规模的交通路网测试了RE算法,验证其适用性和算法效率。
1 算法原理及实现
1.1 双向Dijkstra算法
双向Dijkstra算法即从搜索的源点s和终点t交替使用Dijkstra算法,直到两端点都找到了到达同一节点的最短路径。在节点数量较多的图上,应用双向Dijkstra算法能大幅减少搜索时间。该算法用df(v)和dr(v)分别记录正向和反向算法中节点v至源点s和终点t的距离,用μ记录最短路径长度。算法的基本步骤如下:
步骤1:初始化,对于所有节点v,df(v)=∞,dr(v)=∞,μ=∞;
步骤2:交替使用正向和反向算法,在正向搜索时,若遇到某一被反向搜索作为永久标号点的节点w时,若满足μ>df(v) +l(v,w) +dr(w),则更新μ;反向搜索时同理进行更新;
步骤3:判断是否满足终止条件,若满足则输出最短路径,不满足则返回步骤2。
双向Dijkstra算法的终止条件[5]有两种设置方式,其中一种是正向搜索每前进一步,判断搜索是否满足终止条件,同理反向搜索每前进一步,也判断是否满足终止条件;另一种是完成一个完整正反向搜索后进行终止条件判断,本文选择后者作为终止条件的设置方式。双向Dijkstra算法与单向Dijkstra算法的技术对比见表1。

表1 双向Dijkstra算法与单向Dijkstra算法技术对比Table 1 Technical comparison of bidirectional algorithm and one-way Dijkstra algorithm
1.2 基于reach的预处理方法
1.2.1 相关定义
假定一条由s到t的路径P,并且点v在路径P上,如图1所示。
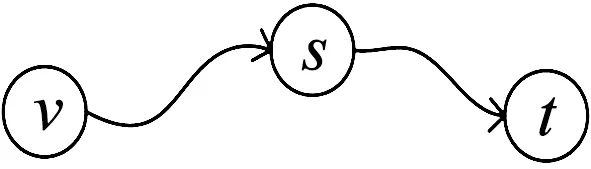
图1 reach的定义Fig.1 Definition of reach
reach(v,P)代表节点v关于最短路径P的reach,其准确值是s到v的子路径长度和v到t的子路径长度中的最小值。
reach(v,P)=min{dist(s,v),dist(t,v)}。
(1)
那么v关于整个图的reach由r(v)表示。
r(v)=max{reach(v,P)}。
(2)
基于reach的预处理方法又称为reach剪枝算法,是指在预处理阶段计算出所有节点的reach值,再根据相应的条件在查询过程中删剪掉不满足条件的节点。
1.2.2 reach值的计算
计算reach值的基本方法是由Gutman等[14]提出,而后Goldberg等[7]提出了改进算法。根据相关研究[7,14],求解reach精确值的效率不高,基于reach剪枝主要用reach上界值(reach bound)来代替精确值,由此产生了许多计算reach上界值的方法,下文分别介绍reach精确值和一种常用的reach上界值的计算方法。
reach精确值的计算过程为:初始化,对于所有节点r(v)=0,对于每一个节点x,生成一个根节点在x的完整最短路径树Tx,对于树上每一个节点v,计算出v到根节点x的距离(depth[v])和v到距离自身最远的子节点v*的距离(height[v]),由(3)计算得出v在以x为根的最短路径树上的reach的值,记为rx(v)。
rx(v)=min{depth[v],height[v]}。
(3)
若rx(v) >r(v),则令rx(v) =r(v),最后得到的r(v)是reach的精确值,计算过程如图2所示。
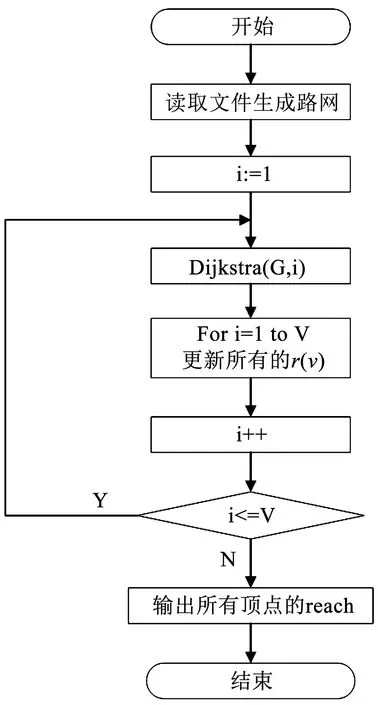
图2 reach精确值计算流程图Fig.2 Flow diagram of calculating exact reach
计算reach上界值的基本过程为:
步骤1:以每个节点x为根节点按照一定条件生成部分最短路径树;
步骤2:计算部分最短路径树上某些节点的reach的上界值和reach的精确值;
步骤3:根据得到的精确的r(v),对图进行收缩修改,保存删除后的图;
步骤4:不断重复步骤1、2、3,不断更新相关节点reach的上界值,直到所有的上界值都被计算出来。
reach上界值与reach精确值相比,其优势在于引入了生成部分树(partial tree)的概念,计算reach精确值时每次都要生成完整的最短路径树,在小网络中,每条完整最短路径树的长度不会很长,但是在上百乃至上千个节点的大网络中,生成完整最短路径树就会消耗大量的时间,而reach上界值算法采用必要条件[7]终止树的生成,在更新队列和计算上界值时节约了时间。因此,在小规模网络中,优先采用reach的精确值算法,而在中等以及大规模网络上,优先采用reach的上界值算法。
1.3 RE算法
1.3.1 算法原理
通常情况下,若一个节点在一条很长的最短路径的中间,那么这个节点的reach值应该是一个很大的数,直观上来看,如果在运行双向Dijkstra算法时处理某一个节点,该节点的reach值太小以至于不能到达目标终点的情况下,可以忽略该点,将其从正向队列和反向队列中删除,从而提高效率,这是RE算法的一般原理。
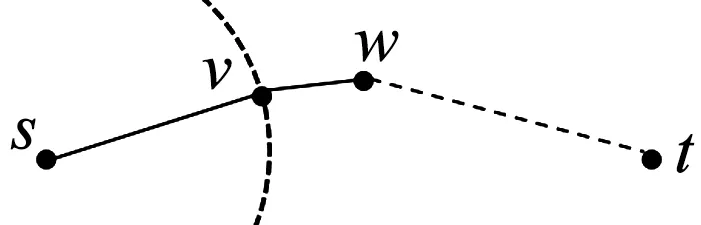
图3 RE算法原理Fig.3 Principe of RE algorithm
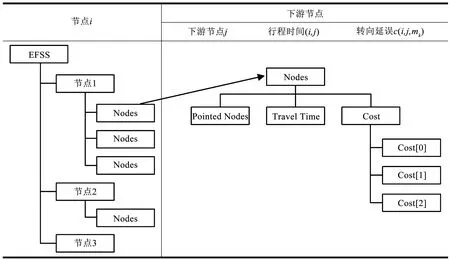
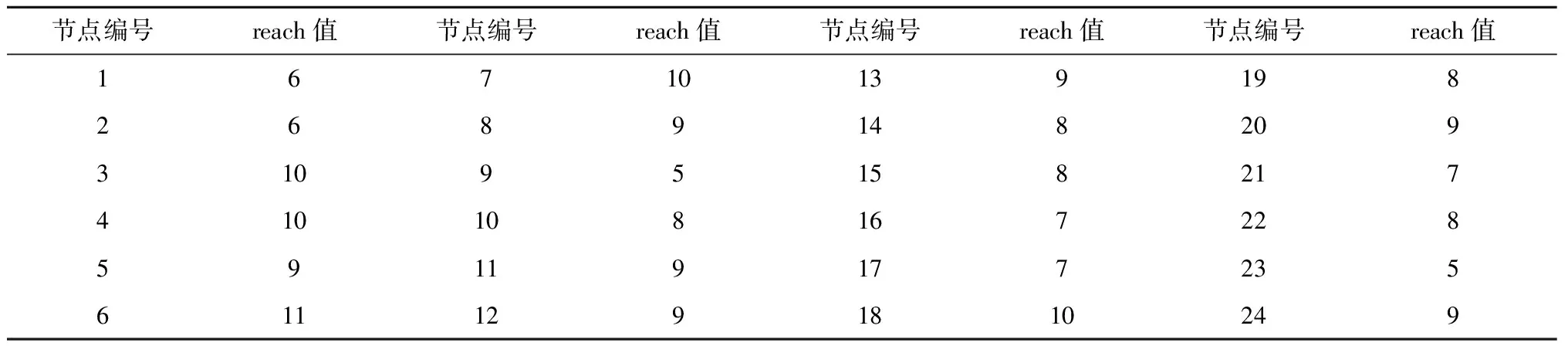
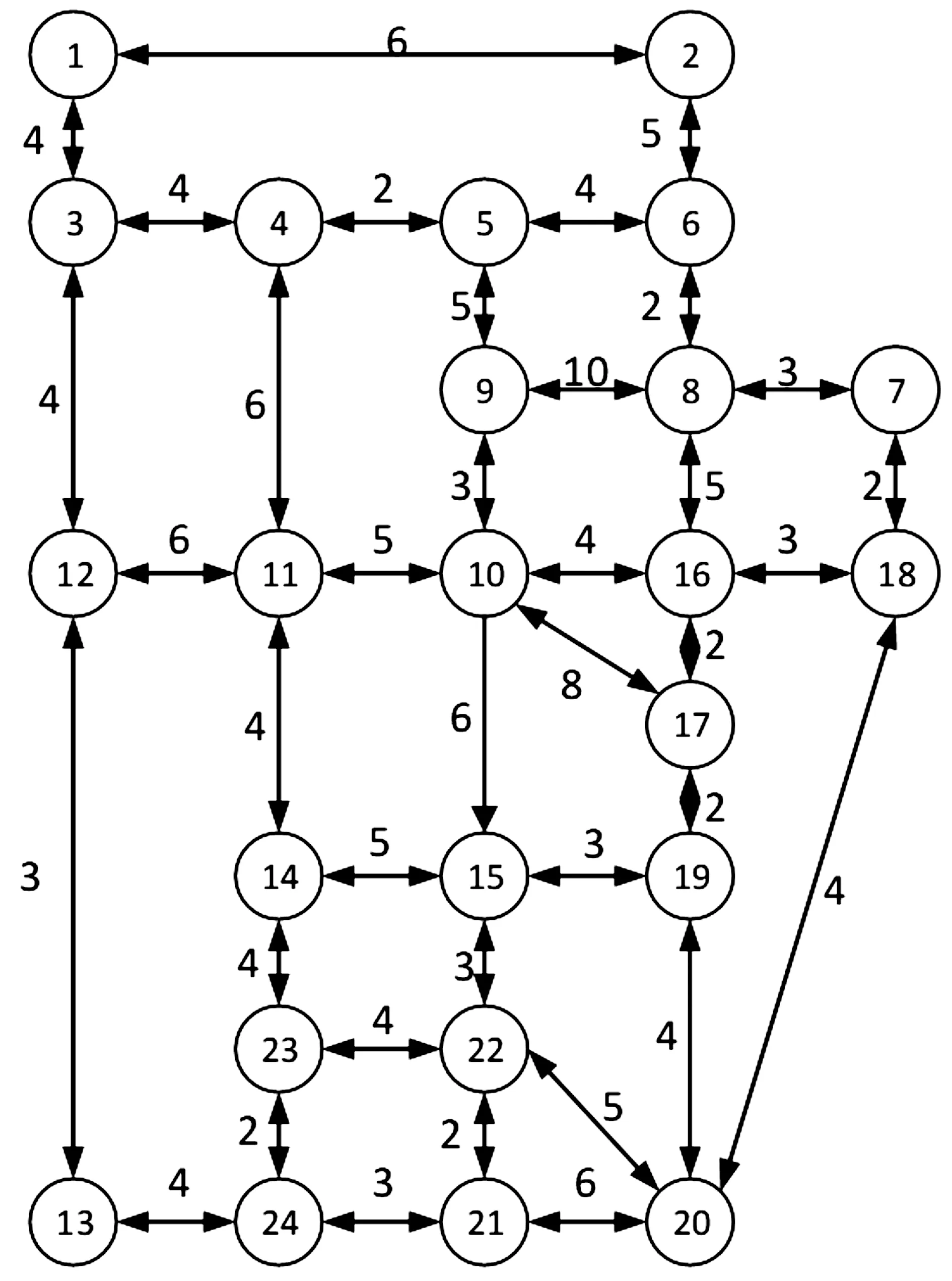
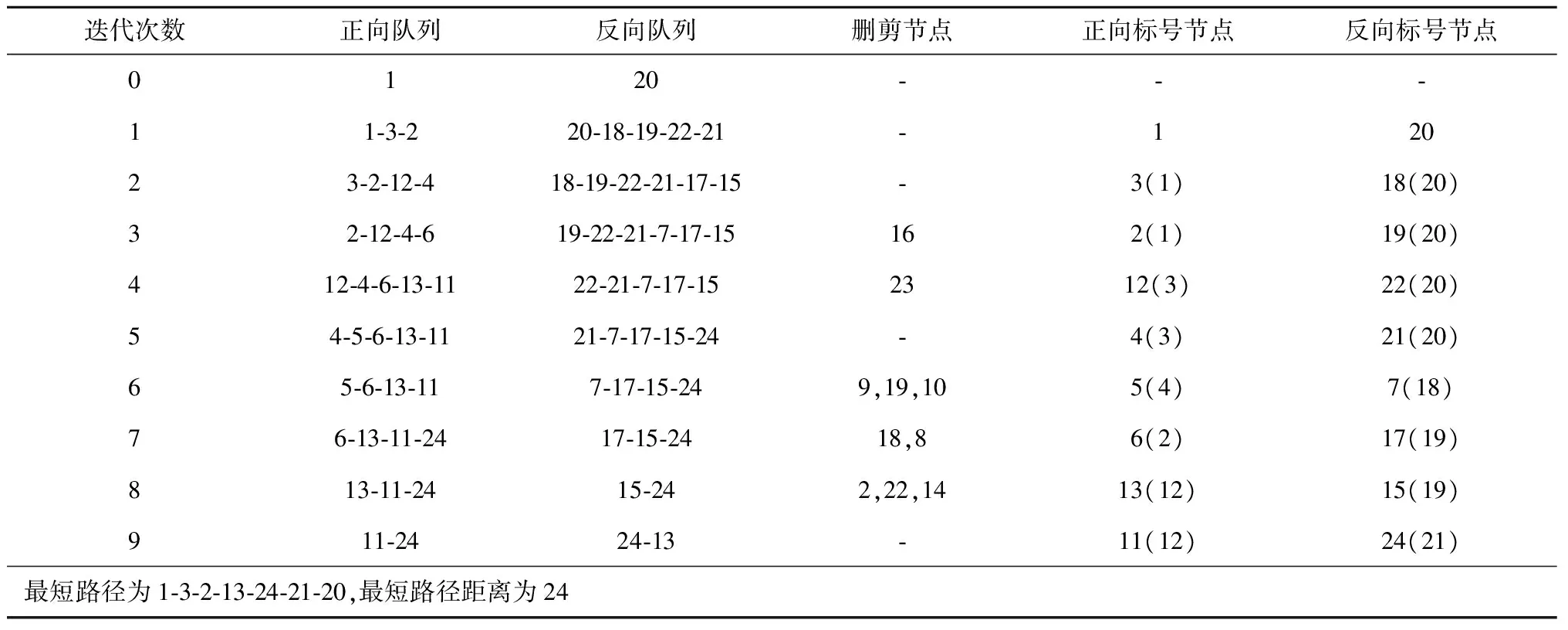
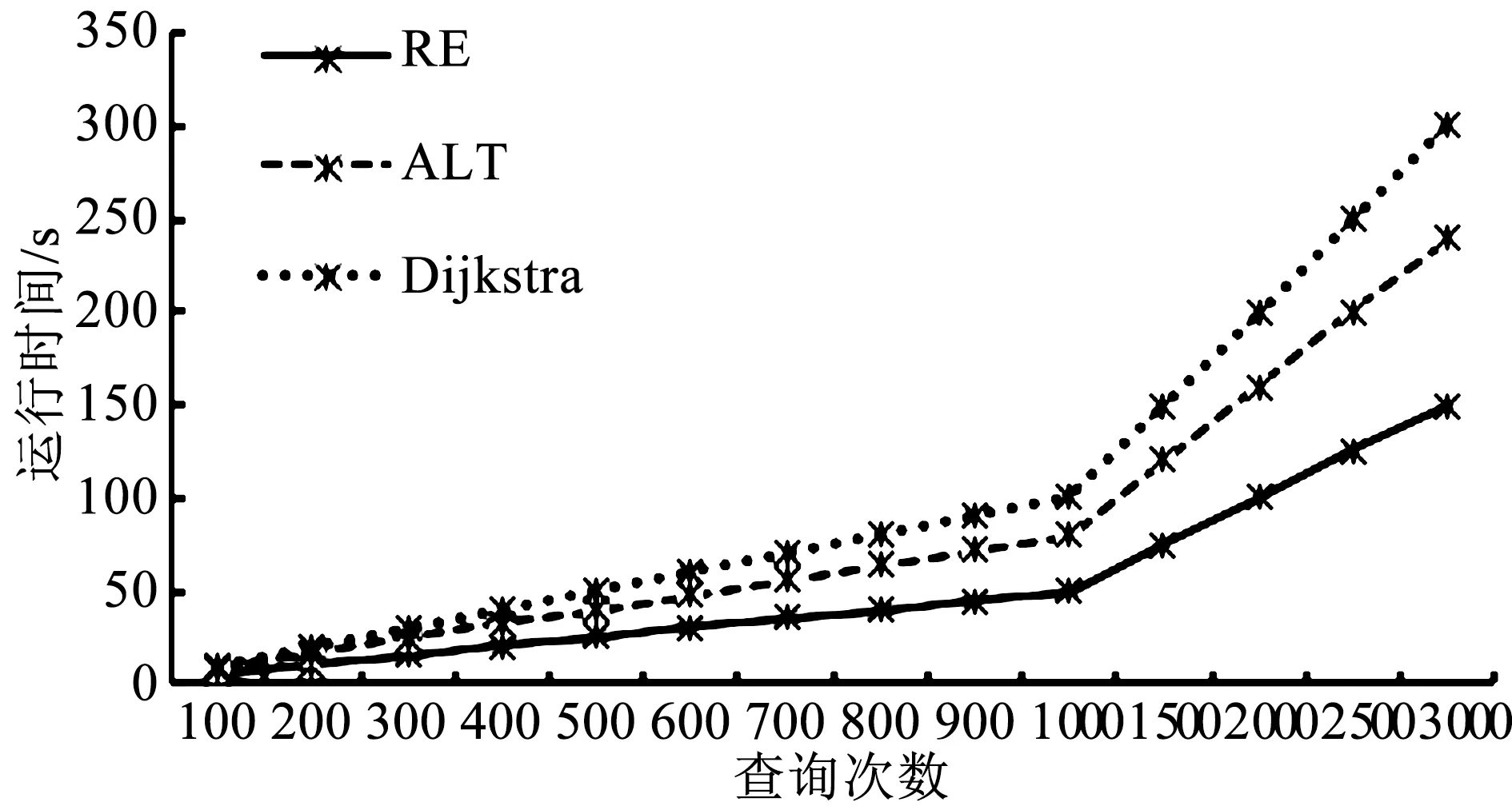
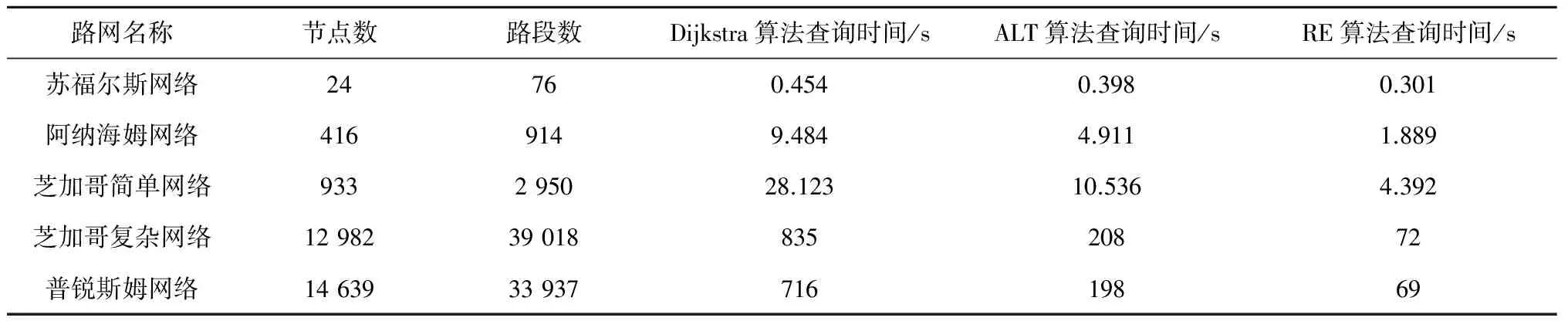
r(w) (4) r(w) (5) 具体删剪方法如图3所示,在一条由s到t的路径上,w为当前需要处理的节点,r(w)为节点w的reach值,如果同时满足公式(4)和公式(5),则将节点w删剪掉,使其不再进入优先队列(priority queue)中,减少搜索过程中队列的节点个数。 1.3.2 算法步骤 假设,在一般路网上,两节点间的路段是双向的并且具有阻抗,首先通过预处理得到rf(v)和rr(v),分别记录前向链表和反向链表计算的reach精确值或上界值,结构体df[V]和dr[V]记录两个方向Dijkstra算法每个节点的编号(ID)、标号距离(label)以及是否成为永久标号点(scaned),结构体df[V]和dr[V]分别放入两个优先队列(priority queue)中按标号距离由小到大自动更新排列。Ωf、Ωr分别作为在正向、反向搜索中一个被标记节点的最小距离标记,即正向队列(forward_q)和反向队列(reverse_q)队首元素的标号距离,prune(v)记录节点是否被删剪,μ1和μ2分别记录正向和反向搜索得到的临时最短路径值,具体RE算法以双向Dijkstra算法为基础,以下是RE算法在该假设下的迭代过程: 步骤1:初始化所有变量,把起点s和终点t放入正向优先队列和反向优先队列; 步骤2:使用正向Dijkstra算法,当处理节点v时,若scanned_r[v]=false、rf(v) 步骤3:使用反向Dijkstra算法,当处理节点v时,若scanned_f[v]=false、rr(v) 步骤4:μ=min{μ1,μ2}; 步骤5:判断是否满足终止条件Ωf+Ωr≤μ,若满足,输出最短路径和距离,否则返回步骤2继续迭代。 将RE算法应用于车载导航路径优化需要构建交通网络,由于实际道路网络是有条件限制的网络[15],比如交通管理手段带来的交叉口禁止转向限制,不同流向车辆之间的干扰和信号控制手段产生的交叉口转向延误等等,为了更好地描述这一问题,本文引入扩展的前向星形结构(extend forward star structure,EFSS)来组建交通网络。 EFSS是在文献[12-13]中提到的一种较为经典的限制网络表示方法,是一种如图4所示的链表结构,在原有的星形链表基础之上加以扩展,加入了对交叉口转向延误的存储,并方便检索。该结构能有效存储交叉口之间的路段阻抗以及交叉口的交通延误,与传统的采用邻接矩阵建立路网拓扑关系相比,EFSS数据结构节省了大量的内存空间,便于预处理和查询搜索。 图4 EFSS数据结构Fig.4 EFSS data structure 本文为使用小规模网络苏福尔斯网络来对RE算法的准确性进行验证,利用EFSS数据结构搭建了如图5所示的交通网络,为方便显示预处理以及删剪节点的过程,该路网设置交叉口转向延误时间为0,两节点间的路段不考虑道路方向不均匀系数的影响,即道路两个方向的阻抗相同,目标是查找节点1到节点20的最短路径距离,首先通过预处理,可以获得如表2所示的每个节点的reach值,预处理时间为16 s。 表2 苏福尔斯测试网络预处理结果Table 2 Results of preprocessing on Sioux Falls test network 图5 苏福尔斯测试网络算例Fig.5 Example of Sioux Falls test network 利用RE算法求解节点1到节点20的最短路径的迭代过程如表3所示。 表3 RE算法求解最短路径迭代过程Table 3 Iterative process for solving the shortest path by RE algorithm 在此算例中,RE算法共完成更新节点18次,在迭代过程中删剪节点10个。用经典Dijkstra算法求解该算例需要更新节点28次,而且需要完成对全部节点的搜索,造成了运算时间和运算空间的浪费。RE算法保证了计算结果的准确性。为了验证RE算法的效率,利用苏福尔斯测试路网随机生成若干对查询节点,选择Dijkstra、ALT和RE算法进行查询,如图6所示,结果表明在小规模路网上,RE算法效率略高于Dijkstra算法和ALT算法。 图6 相同路网下不同算法效率对比Fig.6 Comparison of the efficiency of different algorithms on the same network 为检验新算法在实际交通应用中的适用性,需要在大规模路网上进行测试,本文利用EFSS数据结构建立了5个不同规模的交通网络,利用随机数生成交叉口延误数据与道路阻抗模拟实际路况,并在各个路网上随机生成1 000对节点,用Dijkstra算法、ALT算法和RE算法分别进行查询,并且计算出平均查询时间,得到如表4所示的数据。 表4 不同规模路网上3种算法平均查询时间Table 4 Comparison of average running time of three algorithms on networks of various scales 通过在各种规模的网络中运行RE算法可以发现,路网规模越大,节点数量越多,RE算法的性能越好,在查询速度上的优势越明显。在大规模网络上,RE算法与Dijkstra相比运算效率提升了90% 以上,与ALT算法相比提升了65%,所以RE算法更加适用于大规模的路网,并且随着reach预处理技术的不断改进,算法效率可以得到进一步提高。因此,RE算法在车载导航系统中可以发挥路径规划的作用,也可用于物流配送线路优化等实际问题,具有良好的适用性和应用前景。 本文在经典的最短路径Dijkstra算法的基础上,将双向Dijkstra算法与基于reach的预处理方法相结合形成RE算法,针对RE算法预处理阶段计算reach精确值效率不高,时间较长的问题,引入reach的上界值算法来取代reach的精确值进行计算。本文分析了RE算法的一般步骤,并且利用EFSS链表结构建立了考虑交叉口延误和路段阻抗的交通网络,测试RE算法的性能,将其与Dijkstra算法和ALT算法进行对比。实验结果表明,RE算法在不同规模网络上较Dijkstra算法和ALT算法相比有一定的优势,并且随着网络规模的不断扩大,RE算法其优势也逐步扩大,体现出该算法较好的适用性。 本研究将重点放在算法实现和路网预处理问题上,还有可以优化和深入探讨的部分,比如在构建路网数据时,考虑的道路阻抗与交叉口延误取值为静态值,没有体现路网的动态性,在后续的研究中,考虑引入路段行程时间函数与交叉口的转向惩罚函数,并丰富和完善动态网络加载中的RE最短路径搜索算法,使算法能更准确地描述真实交通状况。 参考文献: [1]DIJKSTRA E W.A note on two problems in connection with graphs [J].Numerical Mathematics,1959,1(1):269-271. [2]HART P E,NILSSON N J,RAPHAEL B.A formal basis for the heuristic determination of minimum cost paths [J].IEEE Transactions on System Science and Cybernetics,1968,4(2):100-107. [3]DORAN J E.An approach to automatic problem-solving [EB/OL].[2017-03-02].https://aitopics.org/search? view=&filters=&sort=score+desc&q=An+approach+to+automatic+problem+solving+. [4]付强.基于预处理的交通网最短路径实时查询研究[D].合肥:中国科学技术大学,2015. [5]PEARL J.Heuristics: Intelligent search strategies for computer problem solving[M].MA,US: Addison-Wesley Pub.Co.,Inc.,1984. [6]GOLDBERG A V,HARRELSON C.Computing the shortest path: A search meets graph theory [M]// Proceedings of the sixteenth annual ACM-SIAM symposium on discrete algorithms.Philadelphia,PA,USA: Society for Industrial and Applied Mathematics,2005:156-165. [7]GOLDBERG A V,KAPLAN H,WERNECK R F.Reach for A*: efficient point-to-point shortest path algorithms [EB/OL].[2017-03-12].http://epubs.siam.org/doi/abs/10.1137/1.9781611972863.13. [8]SANDERS P,SCHULTES D.Highway hierarchies hasten exact shortest path queries [EB/OL].[2017-03-04].https://link.springer.com/chapter/10.1007/11561071_51. [9]GEISBERGER R,SANDERS P,SCHULTES D,et al.Contraction hierarchies: Faster and simpler hierarchical routing in road networks[C]// International Workshop on Experimental Algorithms.Provincetown,MA,USA: [s.n.],2008: 319-333. [10]SCHULTES D,SANDERS P.Dynamic highway-node routing[M]// Proceedings of 6th International Workshop on Experimental Algorithms.Berlin: Springer,2007: 66-79. [11]BAST H,FUNKE S,MATIJEVIC D,et al.In transit to constant time shortest path queries in road networks[EB/OL].[2017-03-12].http://dx.doi.org/10.1137/1.9781611972870.5. [12]ZILIASKOPOULOS A K,MAHMASSANI H S.Time dependent shortest path algorithm for real time intelligent vehicle highway system applications [J].Transportation Research Board,1993(1408):94-100. [13]ZILIASKOPOULOS A K,MAHMASSANI H S.A note on least time path computation considering delays and prohibitions for intersection movements [J].Transportation Research Part B Methodological,1996,30(5):359-367. [14]GUTMAN R J.Reach-based routing: A new approach to shortest path algorithms optimized for road networks[C]// Proceedings of the Sixth Workshop on Algorithm Engineering & Experiments & the First Workshop on Analytic Algorithmics & Combinatorics.New Orleans,LA,USA: [s.n.],2004: 100-111. [15]杜牧青,程琳.考虑交叉口转向延误的最短路径拍卖算法[J].西南交通大学学报,2010,45(2):249-254.2 算法测试
2.1 交通网络构建
2.2 结果分析
3 结语
