冻融循环下含裂隙类岩石冻胀力的力学模型及实验研究

王永岩，张金龙，朱思文

(青岛科技大学,山东 青岛 266601)

寒区裂隙岩体受到冻融循环反复作用影响，在充水裂隙内部反复冻胀、融缩，当冻胀荷载超过岩石抗拉强度后裂隙端部发生宏观断裂，并在端部前缘出现局部区域微裂纹丛集，随着冻融循环深入，宏观断裂不断延展，最终导致整体失稳。因此，冻融循环条件下裂隙岩体失稳过程实质上为反复冻胀荷载沿裂隙端部的疲劳断裂过程。

关于寒区裂隙岩体损伤机制研究，近年逐渐引起国内外学者关注。申艳军等[1]采用相似材料配制 0°、30°、45°、60°和90°的单裂隙类砂岩试样，并对裂隙内部充分饱水，展开 10、20、30和50 次冻融循环实验，而后观测裂隙端部区域在不同裂隙倾角、冻融循环次数下局部化损伤效应差异规律，对裂隙岩体在冻融循环作用下的局部化损伤效应进行分析，并结合断裂力学应力叠加理论，验证了因局部化损伤效应造成的裂隙端部断裂特性及扩展路径规律。刘泉声等[2]针对岩体在冻融循环下裂隙中会经历冻胀力的萌生、发展与消散，裂隙冻胀扩展和岩体冻胀损伤程度受冻胀力控制，基于热力学、渗流理论、界面力学和弹性理论建立了柱形封闭裂隙中冻胀力演化模型，对考虑水分迁移和不迁移两种情况下的冻胀力量值进行了研究。裴向军等[3]对干燥及饱水状态下裂隙岩石冻融的特征展开研究,研究发现裂隙岩石的胀缩率k都随冻融次数的增加而增大，胀缩率的变化程度跟不同岩样的孔隙率特征有关，饱水裂隙岩石在冻融过程中对温度具有较强的敏感性，损伤表现在温度损伤和冻胀损伤。路亚妮等[4]针对不同几何特征的闭合裂隙类砂岩模型试样，进行冻融后的单轴压缩实验，分析裂隙岩体经不同冻融循环次数后的物理力学特性，以及不同裂隙倾角、不同裂隙长度的岩样对冻融岩体强度及破坏形态的影响，虽然对裂隙类岩石试件进行了研究，但仅仅通过实验现象总结出不同裂隙扩展现象[5-11]，未通过理论公式得出冻融循环对含不同角度裂隙试件进行深入分析、以及冻融循环强度、冻融循环次数之间的关系。本文的水泥砂浆类岩石材料为研究对象，结合弹性力学、断裂力学和流体力学相关理论，通过实验验证了冻胀力模型的可行性。

1 实验准备

1.1 含单裂隙类岩石试件制作

图1 试件模具和类岩石材料Fig.1 Specimen mold and similar rock material

图2 实验仪器Fig.2 Experimental apparatus

1.2 类岩石试件的加载仪器

图2加载仪器为TAW-200电子式多功能材料力学试验机(长春朝阳试验仪器有限公司与青岛科技大学联合研制)。

1.3 类岩石试件冻融循环仪器

实验的冻融循环是在恒温条件下进行的，为了提供恒温环境，实验中运用RPH-80型恒温恒湿试验箱(东莞市环瑞环境测试设备有限公司)，冻融循环实验的方法：把恒温恒湿冻融循环试验机设置为首先在温度为-30 ℃条件下冻结6 h，然后在30 ℃的条件下融化6 h，如此反复，即每个冻融循环周期为12 h。该冻融循环试验机的最低温度控制在-30 ℃，湿度设置在100%。

2 类岩石试件冻结过程冻胀力

当水的温度低于其冰点时，水将发生相变，一般来讲孔隙的初始饱和度超过91%，由于孔隙密封，结冰过程中水的体积变化就不能通过水的流动来补偿，水-冰体系体积增加受到岩石骨架的约束，引起孔隙中未冻水的压力及骨架中应力的增加，导致孔隙体积的增大(弹性变形)，当孔隙中应力集中处的应力达到岩石的抗压强度时，裂隙开始扩展，在其扩展前，岩石骨架变形为弹性变形。由于冻胀作用下裂隙的扩展本质上是由冰的生长驱动的(虽然并不一定是由冰直接破裂，但是孔隙以及裂隙中水结冰过程中将会产生一定的冻胀力)，将水与岩石骨架作为冰的外部环境，计算中各参数的符号规定如下：

(1)孔隙的体积为Vp，孔隙中冰的体积为Vi，未冻水的体积为Vw，岩石骨架的体积为Vr，在计算中规定体积减小为正(或压缩)；

(2)水的密度为ρw，冰的密度为ρi；

(3)水在无压条件下结冰前后体积的膨胀系数为λa=9%，而在承压条件下结冰前后体积的膨胀系数为λ，且λ<λa；

(4)水、冰及岩石骨架内的应力分别为Pw、Pi、Pr；

下面将分孔隙(裂隙)扩展和不扩展两种情况，讨论孔隙中水结冰过程中冻胀力的变化以及岩石骨架的响应。

2.1 裂隙不扩展条件下冻胀力计算模型

2.1.1 基本假设

(1)不考虑热力耦合；

(2)孔隙的初始饱和度为100%，即在结冰过程中孔隙内部为水-冰两相系统；

(3)物体在P0的压力下体积为V0。若压强增加(P0→P0+dP)，则体积减小dV。则有K=dP/(-dV/V0)，K被称为该物体的体积模量。水、冰均视作线弹性体，其体积模量分别为Kw(水的弹性模量)和Ki(冰的弹性模量)，且在整个过程中保持恒定；岩石对水和冰的约束简化为弹性模型，忽略岩石骨架中的剪应力和剪切变形，其等效体积模量为Kr(岩石骨架的弹性模量)且在整个过程中保持恒定；

(4)在整个过程中冰始终被水包围，冻结从中心开始，整个过程中水、冰及岩石骨架的应力均相等，即Pw=Pi=Pr。

2.1.2 冻胀力计算模型的建立

在水冰微小的相变过程中，水和冰的体积变化可表示为：

(1)

(2)

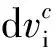
岩石、水和冰体系满足以下条件：

(1)质量守恒(冰和水之间相互转化,质量保持不变)

(3)

(4)

(2)弹性本构关系

由于假设水、冰和岩石骨架均为弹性体，则三者增量形式的本构关系可表示为：

(5)

(6)

(7)

其中，Kr由孔隙的形状和岩石的弹性参数决定；dvr为孔隙体积的变化，在不考虑裂隙扩展的条件下仅为岩石骨架的弹性变形。本质上λ是由冻胀力(水相变为冰体积变大产生的压力)决定的，首先体积为1的水在无约束条件下结冰，冰的体积为1+λa，此时冰压力为零，之后冰的体积被压缩至1+λ，此时冰的压力为pi，冰被压缩的体积为λa-λ。冰的压力可表示为：

(8)

整理可得：

(9)

(3)变形相容条件

水在封闭孔隙中结冰引起体系压力的增加，冰、水和岩石骨架中压力的增加均来源于自身体积的压缩。三者体积的压缩均来源于相变膨胀，因此可得以下相容条件：

(10)

(4)能量转换条件

相变膨胀所做的功=水内力变化+冰内力变化+岩石内力变化。

联合式(2)、(5)、(6)、(7)、(9)、(10)得(11)：

(11)

其中，Vr=Vr0×(P-P0)/Kr=Vr0×Pw/K；上式仅是dVw与dPw之间的关系式。

2.1.3 孔隙等效体积模量的计算方法

预制的矩形裂隙由于裂隙水结冰引起的裂纹扩展视为平面应变问题，裂隙受冻胀力影响，形状发生变化，将变化后的预制的矩形裂隙简化为椭圆柱状孔隙结果。如此简化也不无依据，可参考制作的类岩石试件，其预制的裂纹也并非真正的矩形，其周边由于制作的误差类似于椭圆，经过应力变化后更加近似为椭圆。裂隙的截面变化为椭圆，椭圆的长轴为a,短轴为b。在内部压力p的作用下孔隙发生变形，利用弹性力学理论，结合复变函数可求得p作用下长短轴的位移如下：

(12)

(13)

其中la,lb分别为长、短轴的位移，G=E/2(1+μ)为岩石的剪切模量；μ为岩石泊松比；m=(a-b)/(a+b)，R=(a+b)/2。裂隙的体积应变为

(14)

其中，V是裂隙的体积。

将位移公式(12)、(13)带入(14)可得(15)：

(15)

由于裂隙的变形为弹性，其变形应满足胡克定律，即：

(16)

对比式(15)、(16)可得出:

(17)

上式即为含矩形裂隙岩石等效体积模量的计算公式。

2.1.4 裂隙不扩展条件下岩石弹性模量对冻胀力发展影响

由式(11)可以看出，孔隙水结冰过程中的冻胀力的大小是由孔隙的等效体积模量Kr决定的，而Kr又决定于岩石弹性模量和孔隙的形状决定。其中计算的参数如表1所示。

表1 力学参数Table 1 Mechanical parameters

根据表1的力学参数，假设孔隙水结冰比例为1，根据公式(11)，Ki、Kw为已知量，可以利用MATLAB得到岩石体积模量与体系压力之间的关系如图3所示。

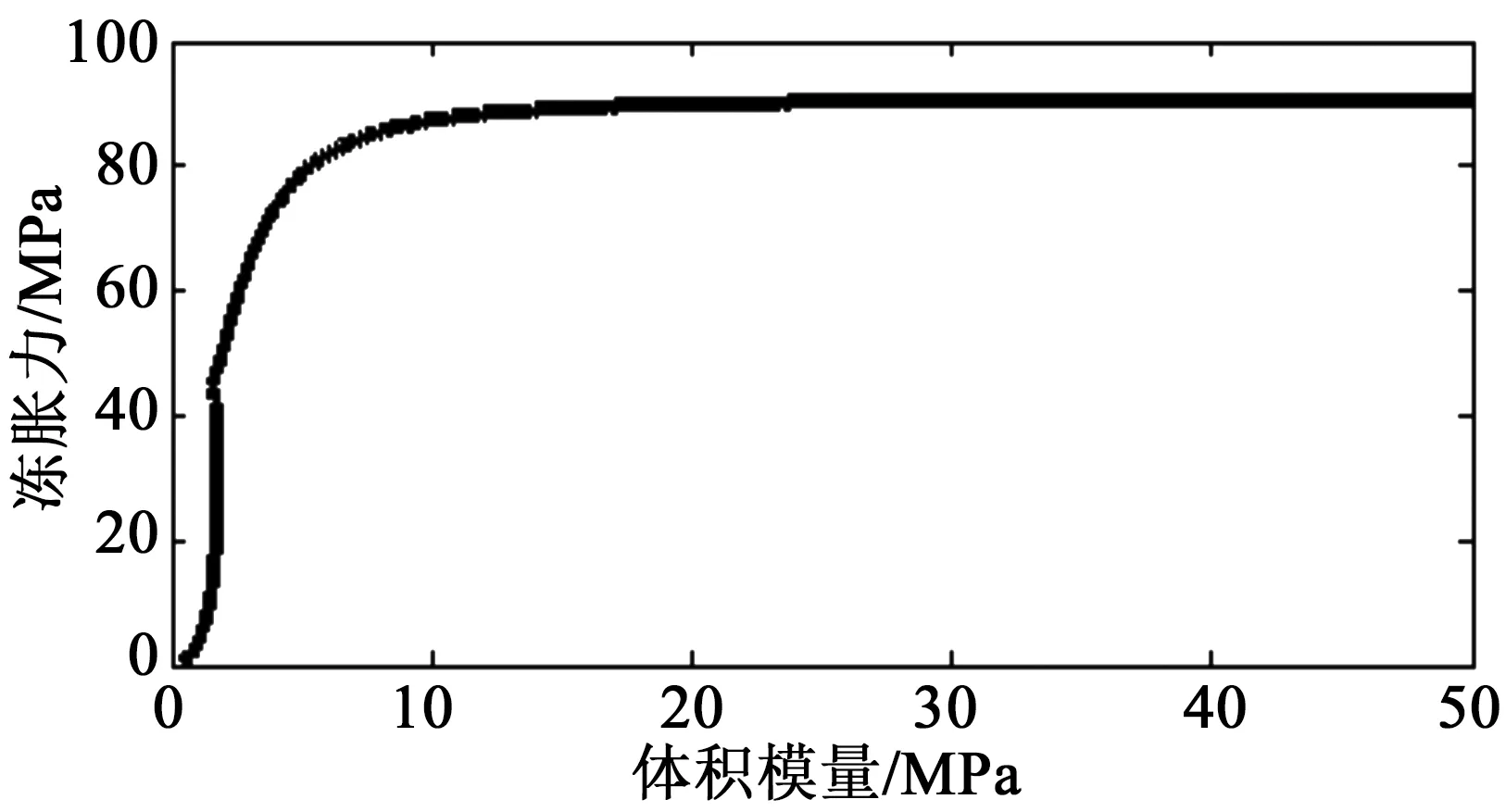
图3 冻胀力和体积模量曲线Fig.3 Frost heaving force and bulk modulus curve

岩石体积模量决定着冻胀力的大小，体积模量越大相同冻结阶段孔隙内冻胀力越大。如图3所示，岩石体积模量和孔隙水完全冻结时最大冻胀力呈非线性的正相关关系，且随着模量的增加最大冻胀力趋向于一特定值，体积模量K和拉伸模量(或称弹性模量)E、泊松比μ之间关系：E=3K(1-2μ)。假设泊松比为固定值，体积模量K和弹性模量E之间为正比例关系，所以冻胀力和弹性模量呈非线性的正相关关系。

3 含裂隙单轴压缩实验

3.1 常规单轴压缩实验

利用TAW-200电子式多功能材料力学实验机对类岩石试件进行单轴压缩实验，采取负荷加载方式，以50 N/s的加载速率进行加载，实验目的测量类岩石试件的弹性模量、泊松比、峰值强度，为类岩石的冻融实验提供必要的信息。

因为本文采取的是类岩石相似材料做成的试件，而且类岩石试件内的裂隙厚度0.8 mm比前人的0.3 mm更宽，所以由于材料和厚度的影响，这里的实验结果与前人的研究结果不同。根据图4～6可知，单轴抗压强度随角度的增加显著增加，含裂隙试件的最低抗压强度大约是完整试件的30%左右，含裂隙试件的最高抗压强度大约是完整试件的67%左右，含贯通单裂隙对试件强度具有较大影响；弹性模量随角度增加逐渐增加，泊松比随角度的增加反而减小。因此，一方面可以验证冻胀力和弹性模量之间的关系，另一方面可以研究不同角度裂隙试件冻融循环后试件强度性能变化及破坏方式。

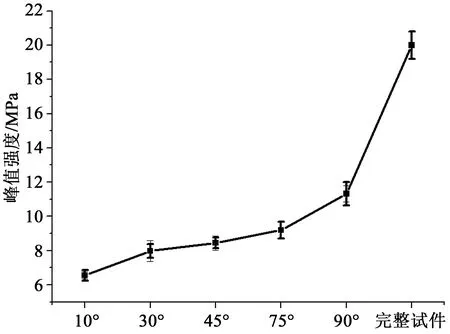
图4 不同裂隙倾角单轴抗压强度Fig.4 Uniaxial compressive strength of specimens with different crack angle

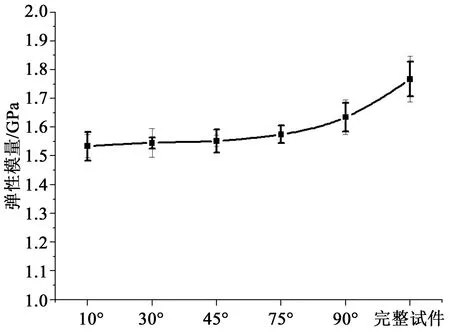
图5 不同裂隙倾角弹性模量Fig.5 Elastic modulus of specimens with different crack angle

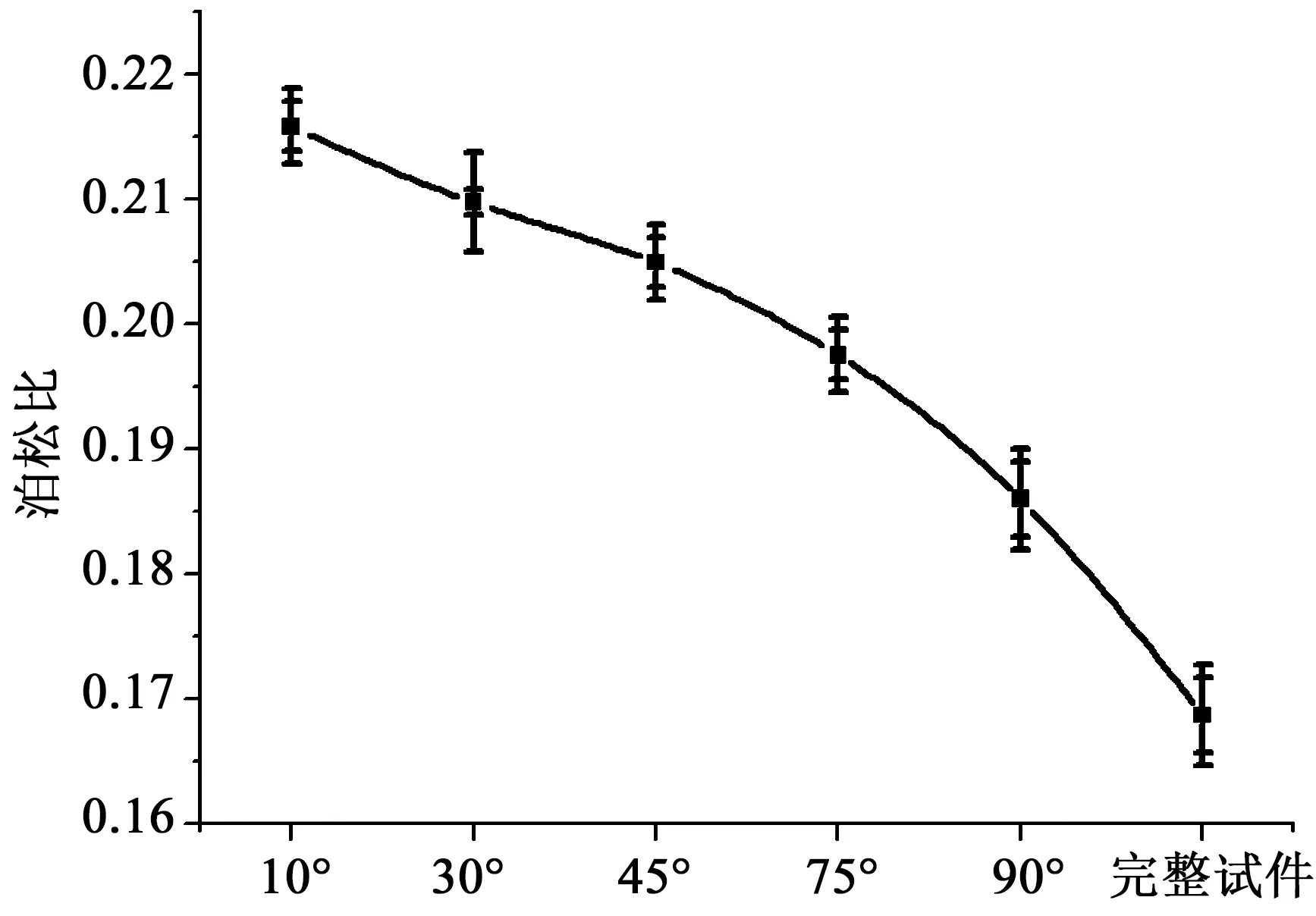
图6 不同裂隙倾角泊松比Fig.6 Poisson's ratio of specimens with different crack angle

3.2 冻融循环后单轴压缩实验

利用TAW-200电子式多功能材料力学实验机对类岩石试件进行单轴压缩实验，采取负荷加载方式，以50 N/s的加载速率进行加载，针对不同循环次数(5次、10次、15次、20次)进行单轴实验，分析冻融循环后不同角度类岩石试件峰值强度，以及相同冻融循环次数对试件峰值强度的影响。

如图7所示,含不同角度的裂隙试件的峰值强度随着冻融循环次数的增加，不同角度裂隙试件的峰值强度逐渐减少，在20次冻融循环阶段含不同角度的裂隙试件的峰值强度出现大幅度下降，不同角度的裂隙试件随角度增加峰值强度仍然保持与常规单轴实验相同趋势，峰值强度随角度增加而显著增加。

由于不同角度裂隙试件的弹性模量不同，所以冻胀力随弹性模量增加呈现增加的趋势，也就是说，弹性模量大的可以承受更大的冻胀力，所以对于不同角度裂隙，0°裂隙更容易冻融循环损伤破坏，90°裂隙试件比0°裂隙试件更能承受冻胀力(图8)，验证了上文提出的冻胀力和弹性模量呈非线性的正相关关系。

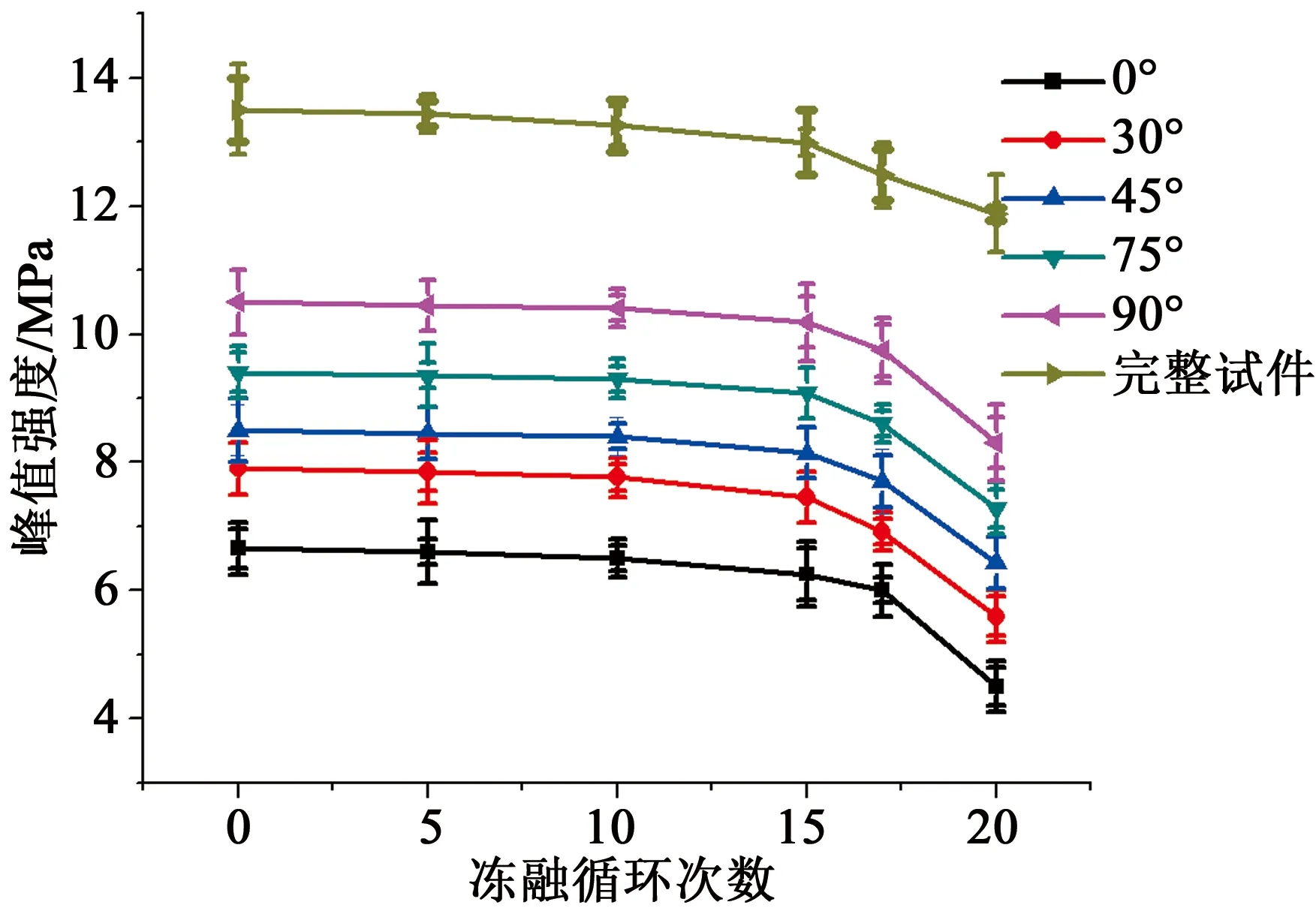
图7 峰值强度与冻融循环次数曲线Fig.7 Curves of peak strength and freeze-thaw cycle frequency

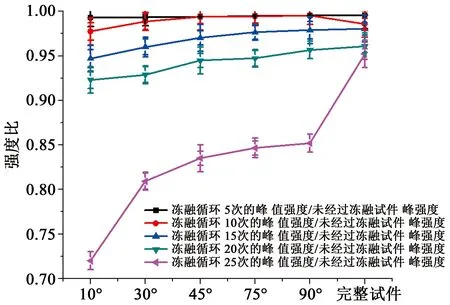
图8 不同裂隙倾角强度比曲线Fig.8 Strength ratio curve

4 结论

(1) 岩石体积模量决定着冻胀力的大小，体积模量越大相同冻结阶段孔隙内冻胀力越大。如图8所示，岩石体积模量和孔隙水完全冻结时最大冻胀力呈非线性的正相关关系，且随着模量的增加最大冻胀力趋向于一特定值，体积模量K和拉伸模量(或称弹性模量)E、泊松比μ之间有关系：E=3K(1-2μ)。假设泊松比为固定值，体积模量K和弹性模量E之间为正比例关系，所以冻胀力和弹性模量呈非线性的正相关关系。

(2) 由于不同角度裂隙试件的弹性模量不同，所以冻胀力随弹性模量增加呈现增加的趋势，也就是说，弹性模量大的可以承受更大的冻胀力，所以对于不同角度裂隙，0°裂隙更容易被冻融循环损伤破坏，90°裂隙试件比0°裂隙试件更能承受冻胀力。

参考文献：

[1]申艳军，杨更社，荣腾龙，等.冻融循环作用下单裂隙类砂岩局部化损伤效应及端部断裂特性分析[J].岩石力学与工程学报,2017,36(3): 562-570.

[2]刘泉声,康永水,黄兴,等.裂隙岩体冻融损伤关键问题及研究状况[J].岩土力学,2012,33(4): 971-978.

[3]裴向军，蒙明辉，袁进科，等.干燥及饱水状态下裂隙岩石冻融特征研究[J].岩石力学，2017,38(7)：1999-2006.

[4]路亚妮，李新平，肖家双.单裂隙岩体冻融力学特性试验分析[J].地下空间与工程学报， 2014，10(6)：593-598.

[5]崔宏环， 刘建坤， 张立群，等.寒区路基改良土冻融循环与荷载耦合作用下损伤力学研究[J].冰川冻土，2016，38(8):1183-1188.

[6]耿珂.冻融循环对寒区隧道结构冻胀力的影响[J].冰川冻土，2013,35(8):913-919.

[7]刘泉声，黄诗冰，康永水，等.低温冻结岩体单裂隙冻胀力与数值计算研究[J].岩土工程学报，2015,37(9)：1572-1580.

[8]路亚妮，李新平，吴兴宏.三轴压缩条件下冻融单裂隙岩样裂缝贯通机制[J].岩土力学，2014,35(6)：1579-1584.

[9]苏海健，靖洪文，赵洪辉.高温后砂岩单轴压缩加载速率效应的试验研究.2014,36(6):1064-1071.

[10]王永岩,朱羽萌,范夕燕，等.孔隙率对页岩相似材料破坏影响的试验研究[J].应用力学学报，2016,33(4)：695-700.

[11]朱羽萌.孔隙率对页岩相似材料破坏影响的试验研究[D].青岛：青岛科技大学，2014.