基于概率协作表示的运动想象脑电分类算法
2018-05-03崔丽霞杨济民常洪丽
崔丽霞,杨济民, 常洪丽
(山东师范大学物理与电子科学学院,山东 济南 250358)
脑机接口(brain computer interface,BCI)是一种不依赖于正常的由外周神经和肌肉组成输出通路的通讯系统[1],可以把大脑发出的信息直接转换成驱动外部设备的控制命令,实现人与外界的直接交流以及对外部环境的控制。脑机接口技术的发展,为那些患有肌肉萎缩性侧索硬化、脑干中风和脊髓损伤等疾病的人,提供了与外界交流的新方法。近几十年来,脑机接口受到了多种学科研究人员的广泛关注,在神经学、生物医学工程和临床康复等领域具有远大的前景[2]。
特征提取是脑机接口系统中的关键技术之一,因为脑电信号具有随机性和非平稳性,单一的分析方法并不能描述信号在时域和频域的联合分布信息。常用的时频分析方法有短时傅里叶变换、小波变换以及S变换等[3]。传统傅里叶变换对信号进行变换后,可以得到信号的频域成分,但得不到信号不同频率随时间分布的信息,在实际应用中存在弊端。短时傅里叶变换是在传统傅里叶变换的基础之上加了一个窗函数,但由于窗函数固定,不能够追踪非平稳信号的动态性。1980年,法国地质物理学家Morlet首次提出小波的概念,继承了短时傅里叶变换的局部化思想,而且窗口大小和形状都可以改变,实现了多尺度分析[4]。1996年Stockwell等[5]提出了一种称为S变换的新的信号处理技术,这是一种具备频率独立分辨率的时频表示方法。S变换是短时傅里叶变换和小波变换的延伸和推广,可以看作是一个具有可变窗函数的短时傅里叶变换,或者是一个连续小波的扩展[6-8]。S变换的优势在于能够提供多分辨率分析,同时保持每个频率的绝对相位,使其非常适用于脑电信号的检测[9]。
基于概率的协作表示方法是一种新的模式识别方法,已经在人脸识别领域成功应用[10]。在Wright等[11]提出的基于稀疏表示的分类方法(sparse representation based classification,SRC)中,以训练样本构造稀疏表示基,利用l1范数最小化作为约束,对测试样本进行稀疏表示,通过比较不同类别的重构误差来实现分类识别。虽然基于稀疏表示的方法具有良好的分类性能,但是Zhang等[12]指出,大多数研究过多强调了l1范数最小化在分类中的作用,真正起到关键性作用的是来自所有类别的训练样本对测试样本的协作表示,而最小l1范数稀疏优化仅使得分类结果更加稳定。在协作表示的分类算法(collaborative representaion based classification,CRC)中,利用最小l2范数代替最小l1范数,使得运算复杂度大大减小。尽管SRC和CRC已经较好应用[13-14],但是对于其分类机制仍然缺乏实质性的解释,而ProCRC从概率的角度分析了CRC的分类机制,结合概率子空间的方法,提出了一种新的模式分类方法[10]。
目前,基于概率协作表示的方法只用于模式识别领域,鲜有用于脑电信号的分类识别中。本文中我们首先采用S变换对脑电信号进行滤波以及功率谱密度的特征提取,然后结合ProCRC进行识别分类,得到了较高的分类准确率,验证了ProCRC算法在脑电信号处理中的有效性和适用性。
1 研究方法
1.1 S变换
S变换可以看成“相位正交”的连续小波变换,时域信号x(t)的小波变换定义为[5,15]:

(1)
其中,w(t,d)是母小波,尺度因子d可以控制小波w(t,d)的窗口宽度,从而控制分辨率。
那么,S变换与小波变换的关系可以表示为:
s(τ,f)=ei2πfτw(τ,d),
(2)
其中,母小波函数定义为:
(3)
由此可见,S变换可定义为尺度可变的母小波和相位因子的乘积构成的连续小波变换。
另一方面,S变换的定义可以由短时傅里叶变换推导得到[16]:

(4)
其约束条件为:

(5)
窗口函数q(τ-t,f)是一个尺度可变的高斯函数,定义为:
(6)
S变换相对于短时傅里叶变换其优势在于,标准偏差σ(f)是频率分量f的函数:σ(f)=1/|f|。因此,窗口函数也是时间和频率的函数,由于窗口的宽度是由频率决定,所以很容易看到,在时间序列上,在较低频率处窗口较宽,在较高频率处窗口较窄,也就是说,这个窗口函数在低频处提供较好的频率分辨率,在高频处提供较好的时间分辨率[17]。
本文主要利用S变换提取脑电信号的功率谱密度(power spectrum density,PSD)作为特征,来准确定位感知运动节律的频谱变化。
1.2 基于概率协作表示的分类器
本文创新地将基于概率协作表示的分类算法应用于运动想象脑电信号的识别中,同时贝叶斯线性判别分析(bayesian linear discriminant analysis,BLDA)和梯度boosting(gradient boosting,GB)与两种分类算法进行对比,验证该算法的有效性。
1.2.1 概率协作表示
假设k类训练样本集合为x=[x1,x2,…,xk],xk是类k的数据矩阵,并且其每一列为一个样本向量。我们认为x是扩展类的数据矩阵,lx是x中所有候选类的标签集,由sx表示x中所有样本协同表示的线性子空间,在协作子空间sx中,每一个数据点h可以表示为:h=xα,其中α是表示向量。
由于x包含所有类的样本,那么协作表示子空间sx比单独每一个类xk的子空间要大的多。因此,尽管所有的xα都属于sx,但是其被标记为lx的置信度是不同的,这取决于表示向量α的构成。
因此提出将sx作为一个概率协作子空间,不同的数据点对应于不同的概率:l(h)∈lx,l(h)是h的标签。若用l2规范得到的α比较小,那么对应的p(l(h)∈lx)会比较大,反之亦然。我们使用高斯函数来定义这样一个概率[10]:
(7)
这里c是一个常量,对应于公式(7)称sx为概率协作子空间,sx内的数据点由α决定其所属类别的概率。
1.2.2 概率子空间外的样本表示
公式(7)定义了位于协作子空间sx内的数据点的概率表示,实际上测试样本y通常位于sx之外。为了评估y属于sx的概率p(l(y)∈lx),先试图在sx内找到一个数据点h,然后计算以下两个概率:p(l(h)∈lx)以及y和h具有相同类标签的概率p(l(h)=l(y)),可以得到:
p(l(y)∈lx)=p(l(y)=l(h)|l(h)∈lx)·p(l(h)∈lx),
(8)
由公式(7)可以求得p(l(h)∈lx),而p(l(y)=l(h)|l(h)∈lx)可以通过h和y之间的相似度来测量,这里采用高斯内核去定义[10]:
(9)
这里κ是常量,高斯核是广泛使用的一种衡量图形中两个顶点相邻相似度的方法,其优点在许多应用中凸显出来,比如数据简化,人脸面部分析,图像聚类等。
由公式(7)~(9),可以推出:
(10)
为了最大化概率p(l(y)∈lx),我们将对数运算应用于公式(10),可以得到[10]:
(11)
这里μ=c/κ,以上公式给出了位于sx之外的测试样本y的概率表示。值得注意的是,公式(11)的表达与协作表示的分类是一致的[12],但是此公式有着明确的概率解释。
1.2.3 特定类子空间的概率
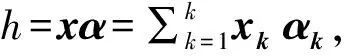
(12)
其中δ是常量,lx为类标签。对于sx空间外的一个查询样本y,可得到l(y)=k的概率:
p(l(y)=k) =p(l(y)=l(h)|l(h)=k)·p(l(h)=k)
=p(l(y)=l(h)|l(h)=k)·p(l(h)=k|l(h)∈lx)·p(l(h)∈lx),
(13)
只要k∈lx,公式(9)的概率与k无关,可得到p(l(y)=l(h)|l(h)=k)=p(l(y)=l(h)|l(h)∈lx),由公式(11)~(13)可得[10]:
p(l(y)=k) =p(l(y)∈lx)·p(l(h)=k|l(h)∈lx)
(14)
其中γ=δ/κ。
1.2.4ProCRC模型
我们需要在sx空间内找到一个公共点,然后最大化联合概率p(l(y)=1,…,k),就可以检测到最高概率的p(l(y)=k),来确定y的类标签。假设事件l(y)=k互相独立,则有:
maxp(l(y)=1,…,k) =max∏kp(l(y)=k)
(15)
运用对数运算,并忽略常数项,可以得到[10]:
(16)
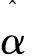
(17)
(18)
其分类规则为:
(19)
以上所述的分类器即为基于概率协作表示的分类器[10](ProCRC)。
分类任务的鲁棒性可以通过使用l1范数来评价损失函数,以上提出的概率协作表示模型中,对公式(9)使用拉普拉斯内核代替高斯内核:
p(l(y)=l(h)|l(h)∈lx)∝exp(-κ‖y-h‖1),
(20)
与ProCRC推导相似,我们可以得到具有鲁棒性的ProCRC(Robust ProCRC,R-ProCRC)模型[10]:
(21)
其分类规则与等式(19)一致。

(22)
注意:I是单位矩阵,那么可以通过T得到α:
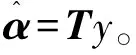
(23)
尽管R-ProCRC模型是凸的,但是没有封闭解,采用IRLS来求解α。首先引入对角加权矩阵wx:
wx(i,i)=1/|x(i,:)α-yi|,
(24)
这里的x(i,:)代表矩阵x的第i行,给定wx,等式(21)可以重新计算为:
(25)
系数向量α更新为[10]:
(26)
交替地更新加权矩阵wx和系数向量α,直到收敛或者达到迭代次数后停止。
2 实验设计
2.1 数据库
本文所提出的算法采用BCI竞赛数据库Ⅲ中的数据集Ⅰ来验证算法的有效性[18]。该脑皮层电图(electrocorticography,ECoG)数据采自于一个病灶性癫痫患者,在被试者的右半球大脑运动皮层表面放置了一个88的网格状铂电极,尺寸大小为8 cm8 cm,包含64个信道。在被试者的大脑中植入的电极要保持一到两周的时间,而且ECoG数据的记录是在一周内的不同的两天完成。在整个实验过程中,被试者坐在舒适的座位上,面对电脑屏幕,并根据实验要求重复想象伸舌头和左小指动这两个动作[19]。每次实验开始时,屏幕中央会出现运动想象任务的图片,为了避免视觉激发电位,数据记录将在提示的0.5 s之后进行。如图1所示,为一次实验的进程[20]。

图1 一次实验的记录过程Fig.1 The recording process of one trial
该数据集的采样频率为1 000 Hz,并包含一个训练集和一个测试集,数据存储格式为“实验次数信道数样本数”,训练集包括278次实验,测试集包括100次实验,由于实验包含两类运动想象任务,训练集中每一类想象任务的实验次数为139次。
2.2 实验流程
本文提出了基于S变换的特征提取和基于概率协作表示的分类器相结合的脑电信号识别的算法,该算法主要包括预处理,特征提取和分类识别等3个部分,基本流程如图2所示。
实验中所用数据库中的脑电信号采样频率较高,为了减少数据存储和提高算法效率,首先对ECoG信号进行1 000 Hz到100 Hz的降采样处理。
其次,采用S变换对数据进行滤波和特征提取,频带范围设置为1 ~ 35 Hz,间隔为1 Hz,这样一方面保留了运动想象脑电信号的主要波段,另一方面起到了滤波作用。然后,计算得到基于S变换的PSD特征,得到的特征矩阵结构为:实验次数64信道PSD特征数目,一次实验当中的特征数为N=CM,C是信道数目,M代表一个信道中的PSD特征数目。
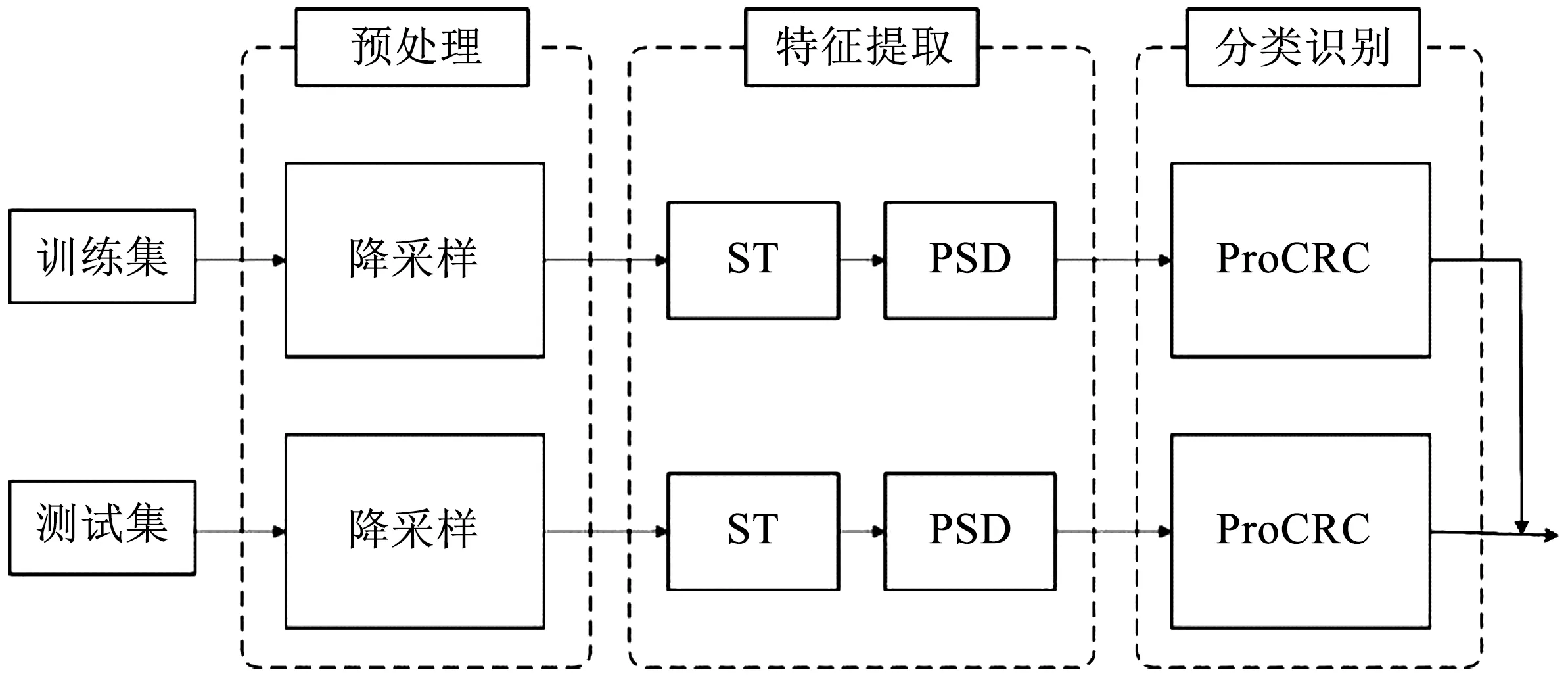
图2 算法框图Fig.2 Block diagram of the algorithm
最后,将提取好的特征矩阵送到ProCRC分类器,实验结果输出0和1,分别代表两种运动想象任务。基于ProCRC算法过程如下:
(1)对训练特征集进行标准化处理,使得特征集的每一列具有单位l2范数;
(2)设置参数γ,μ;
(3)计算投影矩阵
(4)将测试样本投影到T上,获得编码系数α;
(5)引入对角加权矩阵,利用IRLS交替更新系数向量,直到达到设置的迭代次数(与测试样本数目相同);
(6)计算概率
(7)输出所属类别
3 结果分析
BCI系统的评估标准有很多,最常用的评估标准是分类准确率,定义如下:

本文所有的算法程序均在MATLAB环境下运行。在ProCRC中,有两个可调节参数来控制分类的性能,分别为γ和μ。最优的γ和μ值可以提供更好的分类准确率,图3描述了在不同参数γ和μ值下分类准确率的变化。从纵向上来看,对应于不同的γ和μ值,该算法的分类准确率表现出明显的差异性。从横向上来看,当参数μ的值为1时,该算法的分类性能比较稳定,最高可以达到90%,表现出了优异的分类性能。
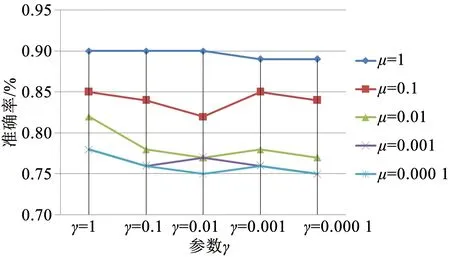
图3 在不同参数γ和μ值下所表现的分类性能对比Fig.3 Comparison of the classification performance under different parameters of γ and μ
良好的特征提取与分类器的最佳匹配能够提高整个算法的性能,为了说明ProCRC具有优异的分类性能,将其与BLDA以及GB分类器进行对比。表1总结了基于ST的PSD特征和不同的分类器相结合得到的分类准确率。Fisher线性判别分析(fisher linear discriminant analysis,FLDA)是为了得到一个最佳判别向量,这个向量使得类间离散度和类内离散度之比最大化,以完成二类或多类的分类问题。BLDA可以看成是FLDA的一个扩展,是基于概率回归网络构成的[21]。GB是一种集成学习算法,可以将多个弱分类器组合成一个强分类器,从而达到提升分类器性能的目的。GB算法在损失函数的梯度下降方向上建立新的弱分类模型,使损失函数越来越小,不断改善分类性能,是一种迭代优化算法[22]。
为了保证比较的公平性,与ProCRC相比较的这两种分类器都是线性分类器。实验结果表明,本文所提出的方法能够得到最好的分类结果,验证了基于概率协作表示的分类算法在脑电信号的分类识别中的有效性。
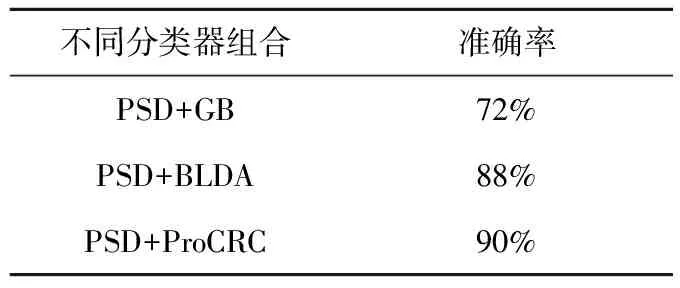
表1 不同分类器的分类准确率Table 1 Classification accuracy of different classifiers
4 结语
本文针对脑电信号的分类识别,提出了一种基于概率协作表示的分类器(ProCRC),具有明确的概率解释。该算法采用了概率协作表示框架,最大化表征测试样本属于每个类别的概率,有效地利用了所有类别的训练样本来推断测试样本的标签类别,具有高效性。
在实验过程中,我们利用BCI竞赛数据库Ⅲ中的数据集Ⅰ来验证所提出算法的有效性。首先对运动想象信号进行了预处理和特征提取,然后将有效的特征和分类器结合,通过与两种典型的BLDA和GB分类器对比,本文提出的ProCRC通过调节参数,可以保持稳定的分类性能,分类准确率能够达到90%,验证了该算法在脑电信号分类识别中的有效性。
脑电信号的识别分类,是脑机接口系统关键技术的研究热点,本文所提出的基于概率的协作表示分类器准确率高,性能稳定,在处理大数据的脑电信号时具有较大的可拓展性,对于研究ProCRC在脑电信号识别领域中的应用具有一定的借鉴意义。
参考文献:
[1]WOLPAW J R,BIRBANME R N,McFARLAND D J,et al.Brain-computer Interface for communication and control[J].Clinical Neurophysiology,2002,113(6):767-791.
[2]GAO S K,WANG Y J,GAO X R,et al.Visual and auditory brain-computer interfaces[J].IEEE Transactions on Biomedical Engineering,2014,61(5):1436-1447.
[3]XU F,ZHOU W,ZHEN Y,et al.Classification of ECoG with modified S-transform for brain computer interface[J].Journal of Computational Information Systems,2014,10(18):8029-8041.
[4]潘泉,张磊,孟晋丽,等.小波滤波方法及应用[M].北京:清华大学出版社,2006.
[5]STOCKWELL R G,MANSINHA L,LOWE R P,Localization of the complex spectrum:the S transform[J].IEEE Transaction on Signal Processing,1996,44(4):998-1001.
[6]YAN Y,ZHU H.The generalization of discrete Stockwell transforms[M]//19th European Signal Processing Conference.[S.l.]:IEEE,2011:1209-1213.
[7]STOCKWELL R G.Abasis for efficient representation of the S-transform[J].Digital Signal Processing,2007,17(1):371-393.
[8]UYAR M,YILDIRIM S,GENCOGLU M T,An expert system based on S-transform and neural network for automatic classification of power quality disturbances[J].Expert Systems with Applications,2009,36(3):5962-5975.
[9]PINNEGAR C R,MANSINHA L.The s-transform with windows of arbitrary and varying shape[J].Geophysics,2003,68(10):381-385.
[10]CAIS J,ZHANG L,ZUO W M,et al.A probabilistic collaborative representation based approach for pattern classification[M]//2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR).[S.l.]: IEEE,2016:2950-2959.
[11]WRIGHT J,YANG A Y,GANESH A,et al.Robust face recognition via sparse representation[J].IEEE transactions on pattern analysis and machine intelligence,2009,31(2):210-227.
[12]ZHANG L,YANG M,FENG X C.Sparse representation or collaborative representation: Which helps face recognition? [M]//2011 IEEE International Conference on Computer Vision.[S.l.]: IEEE,2011:471-478.
[13]SHIN Y,LEE S,AHN M,et al.Noise robustness analysis of sparse representation based classification method for non-stationary EEG signal classification[J].Biomedical Signal Processing and Control,2015,21:8-18.
[14]MIAO M,WANG A,LIU F.A spatial-frequency-temporal optimized feature sparse representation-based classification method for motor imagery EEG pattern recognition[J].Medical & Biological Engineering & Computing,2017,55(9):1589-1603.
[15]McFADDEN P D,COOK J G,FORSTER L M.Decomposition of gear vibration signals by the generalized S-transform[J].Mechanical Systems and Signal Processing,1999,13(5):691-707.
[16]GHAFFARZADEH H.A classification method for pulse-like ground motions based on S-transform[J].Natural Hazards,2016,84(1):1-16.
[18]BLANKERTZ B.BCI Competition III[EB/OL].[2017-10-11].http://www.bbci.de/competition/iii/#data_set_i.
[19]LAL T N,HINTERBERGER T,WIDMAN G,et al.Methods towards invasive human brain computer interfaces[J].Advances in neural information processing systems,2005,17: 737-744.
[20]XU F,ZHOU W,ZHEN Y,et al.Classification of motor imagery tasks for electrocorticogram based brain-computer interface[J].Biomedical Engineering Letters,2014,4(2):149-157.
[21]HOFFMANN U,VESIN J M,EBRAHIMI T,et al.An efficient P300-based brain-computer interface for disabled subjects[J].Journal of Neuroscience Methods,2008,167(1):115-125.
[22]ZHANG Y,ZHOU W,YUAN S,et al.Seizure detection method based on fractal dimension and gradient boosting[J].EpilepsyBehavior,2015,43:30-38.
