基于改进人工蜂群算法优化小波神经网络的短时交通流预测
2018-05-03黄恩潭谷远利
黄恩潭,谷远利
(北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京 100044)
短时交通流预测作为智能交通系统的重要组成部分,日益成为人们研究的重点。近些年来,国内外学者提出了许多短时交通流预测方法,包括卡尔曼滤波预测模型[1]、非参数回归预测模型[2]、时间序列预测模型[3-4]、混沌理论预测模型[5]、K近邻预测模型[6-7]、支持向量机预测模型[8-9]、径向基函数(radial basis function,RBF)神经网络模型[10]、小波神经网络模型(wavelet neural networks,WNN)[11]等等,取得了一定的效果。然而由于交通流量数据的复杂性、强非线性以及不确定性,单一模型难以全面准确地对其进行预测,而组合预测模型能够更好地发挥单一模型的优点,克服自身的缺点,因此,近年来该类模型得到了学者们的广泛关注。
WNN是高度非线性动力学系统,有较优的非线性拟合逼近能力,但存在陷入局部最优解的缺陷。人工蜂群算法(artificial bee colony algorithm,ABC)是Karaboga[12]于2005年提出的一种新型群体智能算法,具有计算参数少、鲁棒性良好和全局搜索能力强等优点,但也存在收敛速度慢、局部搜索能力弱等缺点。本文提出一种改进的ABC优化WNN预测模型,该模型利用ABC弥补WNN权值和阈值选择的随机性缺陷,将WNN良好的非线性拟合能力与ABC较强的鲁棒性结合在一起,对强非线性和不确定性的短时交通流量进行预测,通过实验,证明该模型具有较强的收敛能力和较高的预测精度。
1 小波神经网络
WNN是基于小波变换理论的前馈神经网络模型,本文采用三层紧致结构WNN,将小波函数作为隐含层神经元激励函数,构造出来的WNN拓扑结构如图1所示。
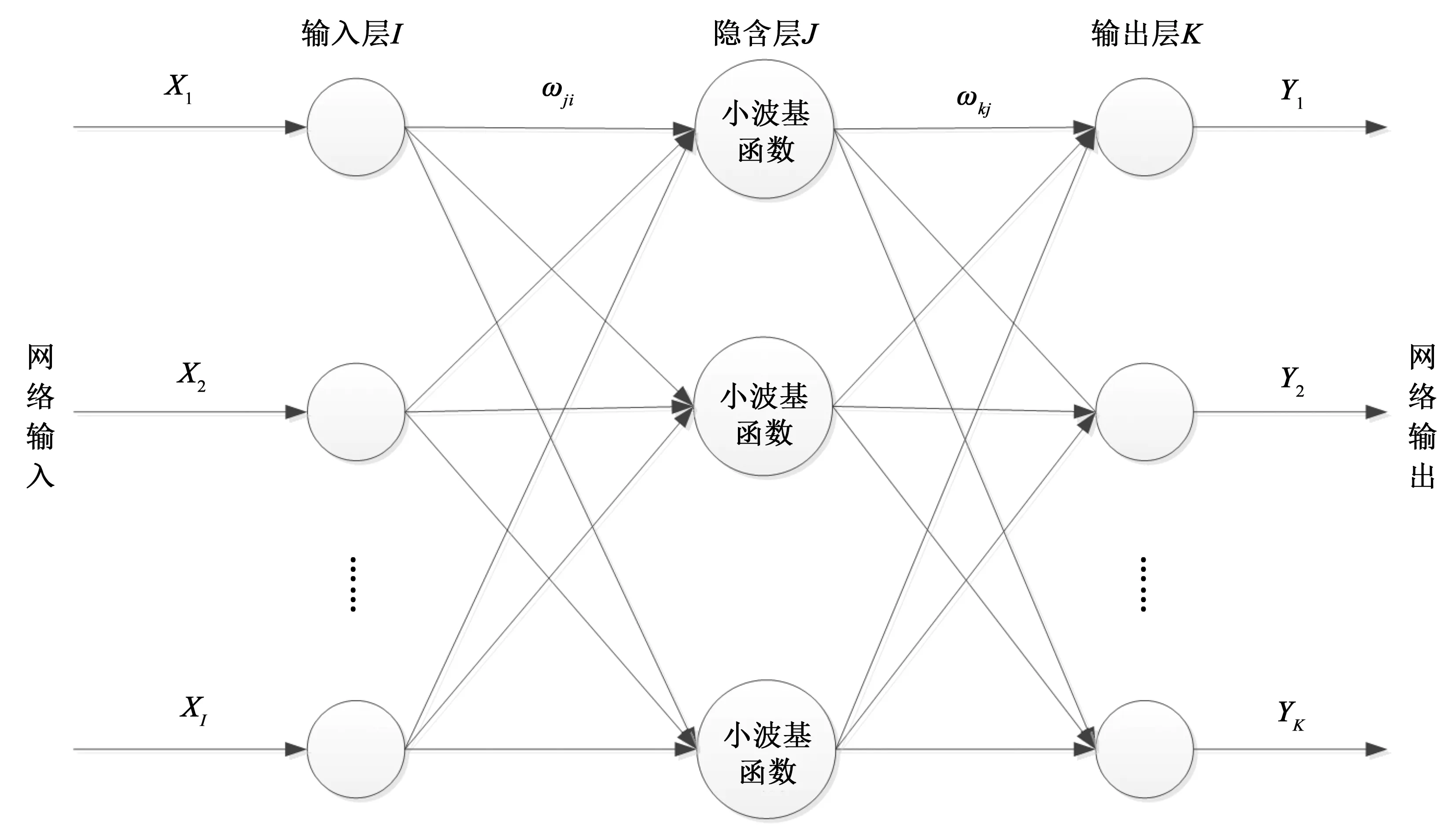
图1 小波神经网络拓扑结构Fig.1 Topology of wavelet neural network
图1中,X1,X2,…,XI为WNN输入参数,Y1,Y2,…,YK为WNN预测输出,ωji为输入层与隐含层之间权值,ωkj为隐含层与输出层之间权值。隐含层神经元激励函数为Morlet母小波基函数,其表达式如式(1)所示。
y=cos(1.75x)exp(-x2/2)。
(1)
当输入参数为xi(i=1,2,…,I)时,隐含层输出如式(2)所示。
(2)
式中,h(j)为隐含层第j个节点输出值;J为隐含层神经元数;ωji为输入层与隐含层之间权值;hj为隐含层神经元j的小波基函数;aj为小波基函数hj的伸缩因子;bj为小波基函数hj的平移因子。
WNN输出层第k个神经元输出为式(3)所示。
(3)
式中,h(j)为第j个隐含层神经元的输出;K为输出层神经元数;ωkj为隐含层与输出层之间权值。
网络输出误差能量函数如式(4)所示。
(4)
2 人工蜂群算法
ABC中,搜索解的蜂群主要包含引领蜂、跟随蜂和侦察蜂三种。引领蜂负责寻找蜜源,当发现了新的蜜源时,引领蜂会将采集到的信息传达给跟随蜂,跟随蜂根据信息采用某种策略选择蜜源进行开采,放弃部分蜜源。被放弃蜜源的引领蜂则会变成侦查蜂,重新开始搜索新蜜源。
ABC中,在求解函数优化问题时,引领蜂或蜜源的数量即为解的数量,蜜源的位置对应优化问题的可行解,蜜源的花蜜量对应着解的适应度,蜂群在规定范围内寻找最优蜜源的过程就是ABC在规定区间内搜索函数最优解的过程。用ABC求解函数最优化问题过程如下:
(Ⅰ)种群初始化阶段
对于全局函数优化问题,有
minδ=f(X)。
(5)
设在D维的搜索空间中,ABC算法随机产生N个解,即N为引领蜂数或蜜源数。每个解Xi(i=1,2,…,N)为一个D维向量,表示第i个蜜源的位置,即Xi={xi1,xi2,…,xiD},其中,D为优化参数个数。
(Ⅱ)引领蜂阶段
引领蜂在蜜源附近搜索产生新蜜源,根据贪婪选择更新蜜源,如果新蜜源优于原蜜源,则记住新蜜源的位置,忘记原蜜源,否则保留原蜜源。新蜜源的搜索如式(6)。
vij=xij+φij(xij-xkj),
(6)
式中,i、k∈{1,2,…,N}且i≠k,j∈{1,2,…,D};vij为新蜜源;xij为当前蜜源位置;xkj为当前蜜源xij邻域内随机搜索的一个蜜源;φij为[-1,1]之间的随机数。
(Ⅲ)跟随蜂阶段
引领蜂将信息传达给跟随蜂,跟随蜂根据花蜜量的丰富程度按照概率pi选择蜜源,并生成新蜜源。若新蜜源优于原蜜源,则选择新蜜源,否则保留原蜜源。利用公式(6)产生新蜜源,利用公式(7)计算概率pi。
(7)
式中,hi为第i个蜜源的收益度,即适应度值。
(Ⅳ)侦察蜂阶段
当一处蜜源经过多次搜索迭代却依然没有被改进之后,该位置会被放弃,相应的引领蜂转为侦察蜂重新开始寻找解。搜索新解的方法如式(8)。
(8)
3 改进的人工蜂群算法优化小波神经网络
WNN存在易陷入局部最优,收敛速度较慢等缺点。ABC收敛速度快,但求解过程缺乏局部信息从而难以得到较高精度。本文提出一种改进的ABC,在标准ABC基础上加入差分进化算法的变异操作和遗传算法的选择算子、交叉算子和变异算子,以此平衡算法的全局和局部搜索能力,并用来优化WNN的参数,形成改进的ABC-WNN预测模型。利用改进ABC优化WNN的权值与阈值能够降低参数选择的随机性,加快了模型收敛速度,提高了对复杂交通流的预测速度和精度。
3.1 基于差分进化算法的改进
由Storn等[13]于1995年提出的差分进化(differential evolution algorithm,DE)算法是一种计算参数少,能够进行随机和并行计算的有效全局搜索算法。DE算法通过对种群初始化、变异、交叉和选择等操作不断循环迭代,往期望最优解方向进行搜索,从而得到合适的解。其中,种群新个体的产生主要靠DE算法的变异过程,变异过程如式(9)所示。
Vi(g+1)=Xr1(g)+F·(Xr2(g)-Xr3(g)),
(9)
式中,i,r1,r2,r3表示种群内4个不同个体,i=1,2,…,N,N为种群中个体数目;F为缩放因子;g为进化代数。
根据式(9)可得,DE算法有向种群个体学习的能力,当算法快要收敛的时候,个体之间差异较小,新个体会在原有个体附近搜索,因此DE算法有良好的局部开采能力。在ABC中,由于引领蜂和跟随蜂两个阶段均要通过式(6)产生新的个体,而式中参数都是随机的,新个体的产生有着较大的随机性,所以式(6)有较强的全局搜索能力,但也说明ABC的局部搜索能力较弱。因此,ABC可以学习DE算法的变异操作产生新个体,提高算法的开采能力。在此,将DE算法的变异过程即式(9)修改为式(10)。
vij=xbest+F·(xij-xkj),
(10)
式中,xbest表示当前的最优蜜源;F为缩放因子;其他参数含义同式(6)。
通常来说,缩放因子F的取值是根据实际经验来选取,在[0.5,1]的范围内取值能够保证较高的求解精度和较好的收敛速度。但DE算法对参数的选择十分敏感,不同实际问题的情况下参数的选择对算法求解结果有较大的影响,当F取值较大时,算法能在较大区域内搜索,有利于保持种群多样性,全局搜索能力强,但求解精度较低。F取值较小时,搜索受到扰动较小,能够加强局部搜索能力,但是算法容易早熟,种群也容易降低多样性。因此,为了平衡算法的全局搜索和局部搜索能力,引入粒子群算法中自适应惯性权重的思想,使缩放因子F的取值采用非线性的动态惯性权重系数公式,其表达式如式(11)所示。
(11)
式中,Fmax和Fmin分别表示缩放因子F的最大值和最小值,在本文中,令F取值范围在[0.5,1]之间;f表示个体当前的目标函数值;favg表示当前所有个体的平均目标值;fmin表示当前个体最小目标值。F的取值不再固定而是能够随着各个体的目标函数值进行改变。在求最小化目标函数最优解过程中,个体目标函数值小于种群平均目标函数值,说明个体较优,取较小的F,使算法在靠近最优解范围内搜索。个体目标函数值大于种群平均目标函数值时,取较大的F,增大算法搜索范围。
引领蜂搜索阶段仍然采用式(6)进行搜索,而跟随蜂阶段则采用式(10)进行搜索。式(10)考虑到了当前最优解对产生新个体的影响,采用自适应缩放因子平衡算法全局搜索与局部搜索能力,保证了ABC算法开发能力的同时也提高了算法的局部开采能力。
3.2 基于遗传算法的改进
在DE算法中,缩放因子F的取值影响着算法的收敛速度和种群的多样性。为了降低F取值的随机性对交通流预测的影响,提高整个预测模型的鲁棒性和容错性,引入遗传算法[14]中的选择算子、交叉算子和变异算子,提高ABC算法的局部搜索能力和保持种群的多样性。改进方法为,在跟随蜂阶段引入遗传算法中的选择算子和变异算子,在侦察蜂阶段引入遗传算法中的选择算子和交叉算子。主要操作过程如下。
3.2.1 选择算子
用轮盘赌法对蜂群进行选择,蜂群中每个个体被选择的概率同式(7)。计算各个蜜源的累积概率并构造一个轮盘,如式(12)所示。
(12)
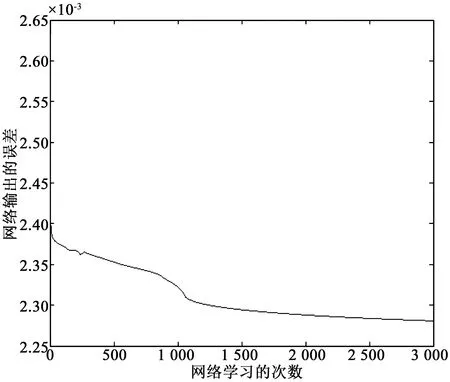
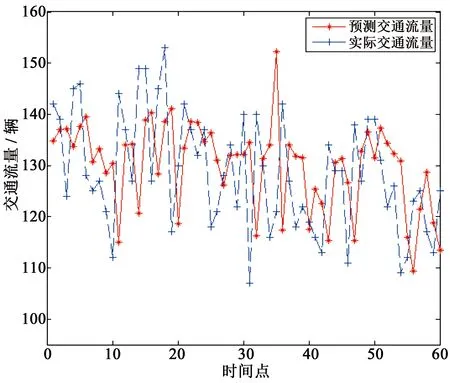
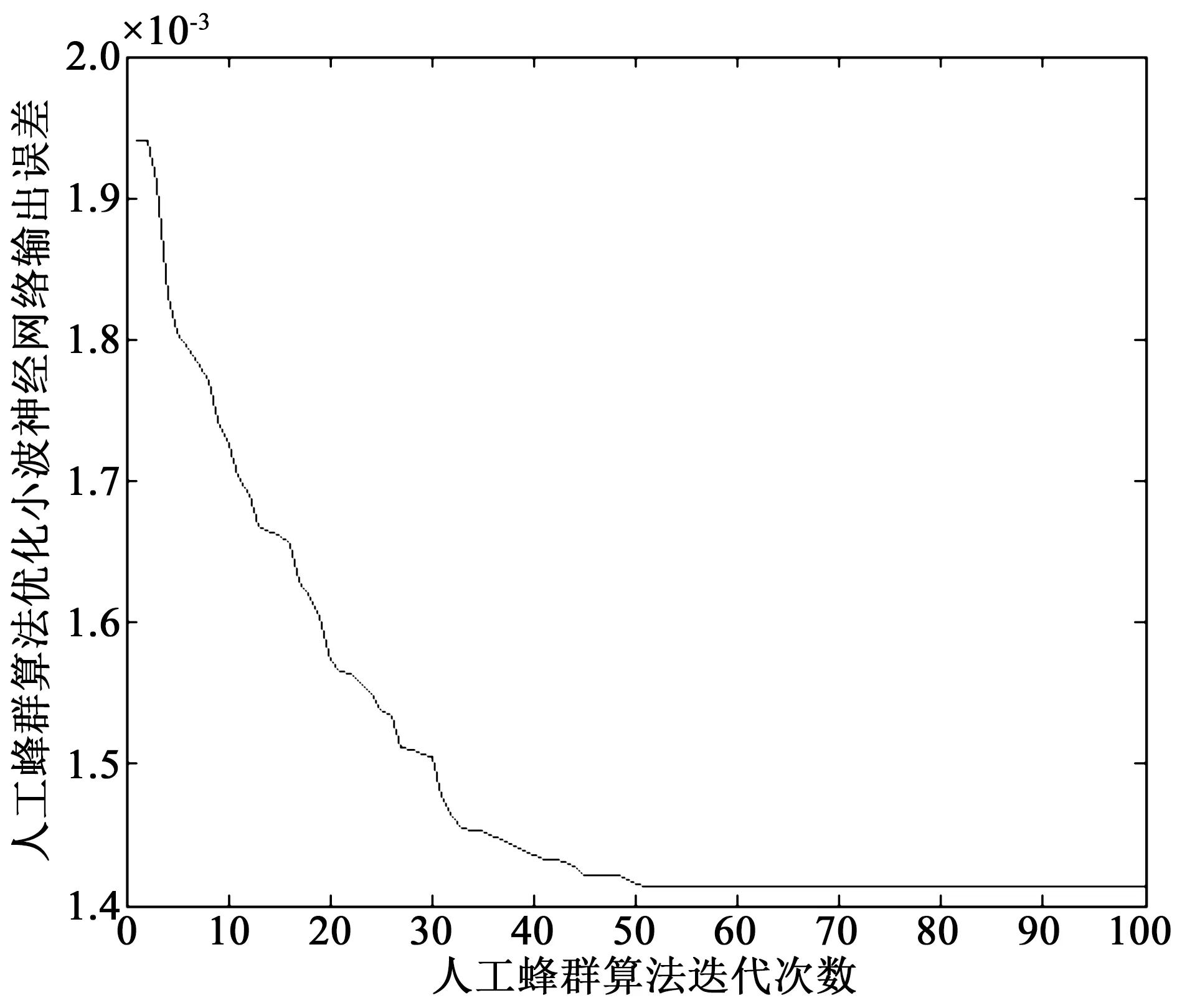
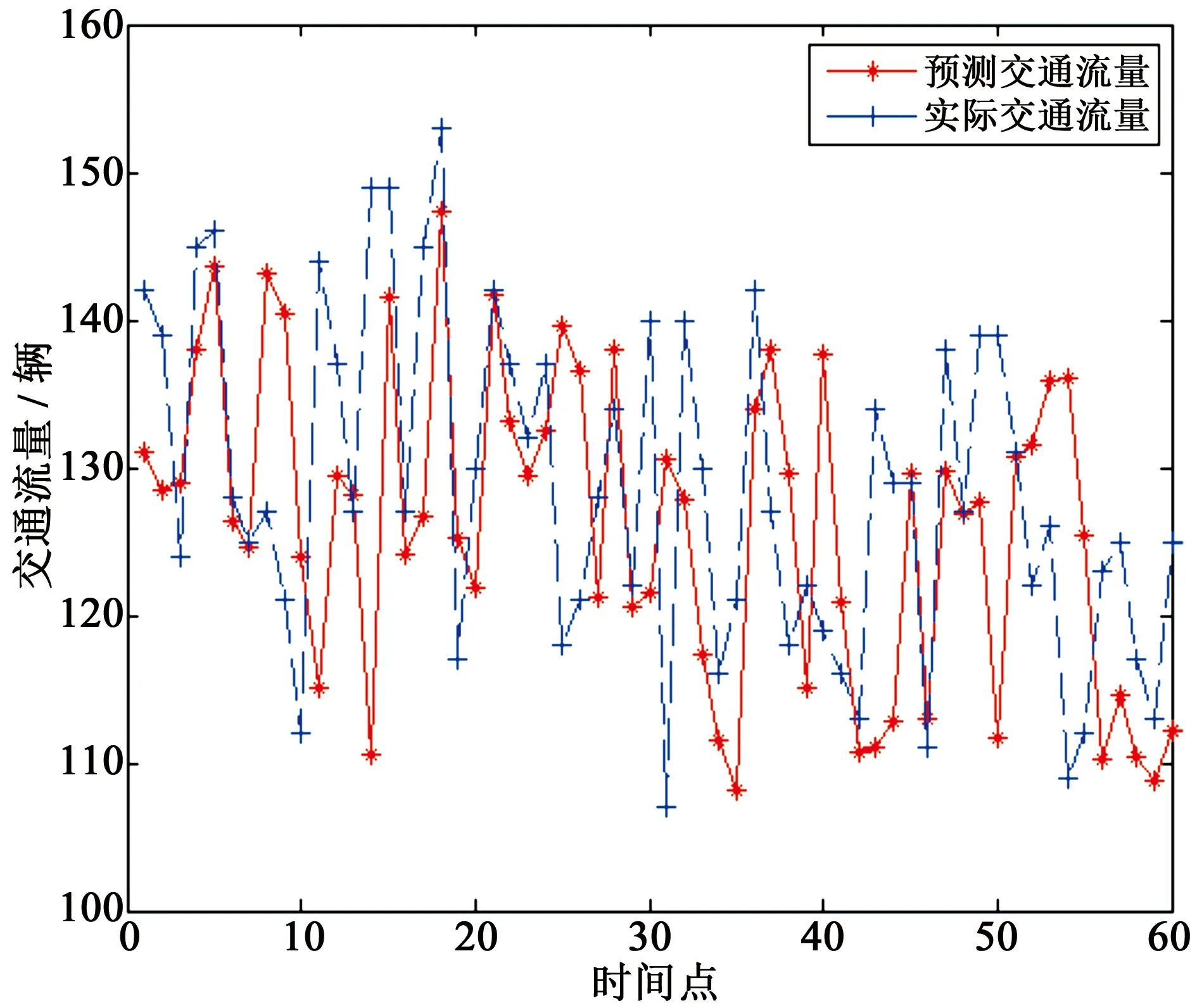
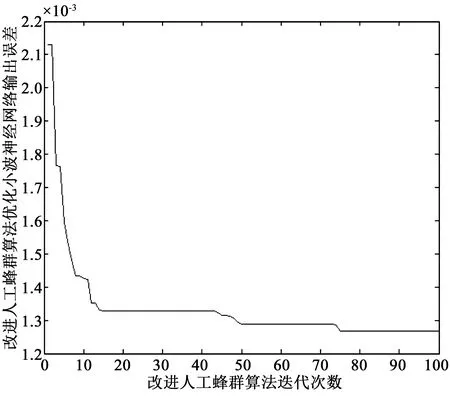
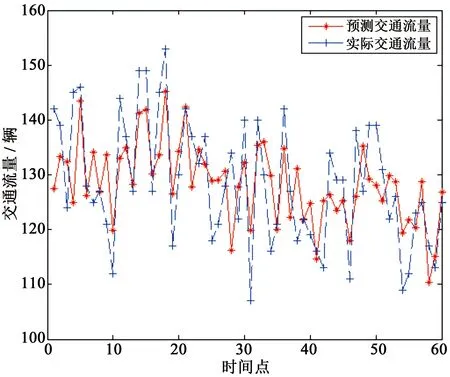
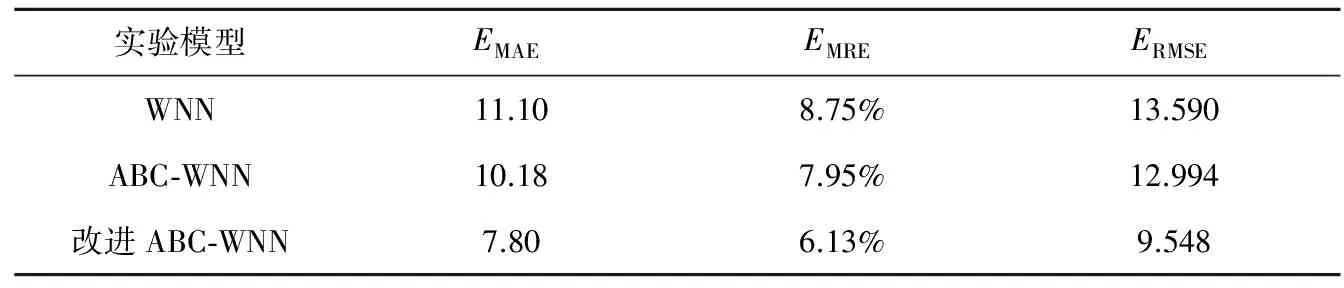
式中,qi为累积概率;N为种群规模。产生一个[0,1]区间内的随机数j,若随机数j满足qi-1≤j 3.2.2 交叉算子 图2 单点交叉Fig.2 One-point crossover 对选择出来的蜂群进行一定概率的交叉,交叉方法采用单点交叉,如图2所示。m表示单个染色体上的基因数,交叉点在第三和第四基因位之间,交叉后产生新的个体。是否进行交叉由交叉概率决定,交叉点位置也是随机产生的,期望让优良基因进行相互组合产生良好个体。因此,在侦察蜂阶段引入交叉算子,有利于减少因蜜源被放弃和跟随蜂阶段伸缩因子F取值不合理而造成的对种群多样性的影响,同时能加强跳出局部最优解能力,提高全局搜索能力。交叉后,将原蜜源与交叉后蜜源进行比较,充分利用旧蜜源的有用信息,留下适应度大的蜜源,淘汰适应度小的蜜源,使整个蜂群往更优的方向进行搜索进化。 3.2.3 变异算子 ABC的跟随蜂阶段是整个算法中重要的局部搜索过程,为了进一步提高跟随蜂阶段算法的局部搜索能力,引入变异算子。本文采用单点变异方式,即将个体基因串上的某个基因值进行改变。算法进入早熟收敛的时候,通过变异操作,可以让跟随蜂进入不同邻域搜索,更有可能搜索到全局最优解。同理,变异后,将原蜜源与变异后蜜源适应度值进行比较,留下适应度大的蜜源,淘汰适应度小的蜜源。 本文中,改进的ABC-WNN预测模型主要步骤如下: (a)对种群进行初始化,随机产生N个初始解xi(i=1,2,…,N,N为优化参数总数),引领蜂与跟随蜂数目均为N。记录各个蜜源的花蜜量,即各个解的适应度值,并将最优解记录下来,设定最大迭代循环次数M,模型的选择、变异、交叉过程采用实数编码; (b)令控制迭代循环参数C=1; (c)引领蜂根据式(6)开始进行随机搜索产生新解vi,计算新解的适应度值,将其与xi的适应度值进行比较,若vi适应度值比xi大,则选择新解vi,否则选择原有解xi; (d)根据式(7)计算蜜源的选择概率pi; (e)跟随蜂根据选择概率pi选择蜜源,更新当前最优蜜源,利用式(10)在当前最优解邻域范围内搜索新解,计算适应度值,对新解与原有解进行贪婪选择,得到新的一组解xi; (f)计算解xi的适应度大小,并按照轮盘赌方法进行选择,将选择出来的蜜源按照变异概率进行变异操作,生成新蜜源vi; (g)计算变异后新蜜源vi和原蜜源xi的适应度值,进行贪婪选择,选择适应度大的蜜源; (h)判断是否有需要放弃的蜜源,若存在需要放弃的蜜源,则引领蜂变成侦察蜂,根据式(8)搜索新的蜜源代替被放弃的蜜源; (i)计算当前蜜源xi的适应度值,按照轮盘赌方法进行选择,将选择出来的蜜源按照交叉概率进行交叉操作,生成新的蜜源vi; (j)计算交叉后新蜜源vi和原蜜源xi的适应度值,进行贪婪选择,选择适应度大的蜜源; (k)记录迄今为止适应度最大的蜜源; (l)C=C+1,如果C>M,则算法停止迭代,输出最优结果,否则转第(c)步; (m)将输出的参数结果赋予WNN,使用WNN对交通流进行预测。 WNN良好的非线性拟合能力能够在理论上以任意精度逼近非线性函数,再加上较强的自学习和数据并行处理能力,可以用来预测同样强非线性的短时交通流量,在预测过程中,WNN通过网络学习能够存储大量交通流量样本数据中蕴含的映射关系,并通过不断的参数修正来进行短时交通流预测。由于WNN的修正采用梯度下降法,以误差函数负梯度方向对网络相关参数进行修正。当网络拓扑结构确定后,网络相关参数的取值对WNN的训练次数和输出结果影响较大,未经优化的随机初始化值会使WNN的收敛速度变慢,且容易使预测结果为非最优解无法准确反映交通流的变化过程。利用改进ABC-WNN的组合模型能够充分结合多种模型的优点,提高了预测模型的容错性。通过优化WNN的权值和阈值,能改善网络的整体性能,让模型更加接近交通流的实际变化情况,使之在输入交通流数据后能够减少WNN的训练次数,提高短时交通流的预测速度和预测精度。本文改进ABC-WNN预测模型的交通流预测步骤为: (Ⅰ)确定输入参数。输入参数为前几日对应时间段交通流量的历史数据,以及预测时间点前几个时刻交通流量数据; (Ⅱ)确定输出参数。输出参数为规定预测时间点交通流量; (Ⅲ)模型训练。利用前几日对应时间段交通流量历史数据对模型进行训练; (Ⅳ)模型预测。将预测时间点前几个时刻交通流量数据输入训练好的模型中进行预测,并与实际交通流量进行对比,统计误差。 在北京市二环路东四十条桥北绿地内中航大厦南20 m处设置一微波车辆检测器,统计2013年4月16日至2013年4月30日共15天,全天00:00—24:00时段通过车检器的车流量,每2 min统计一次。本文对每天晚高峰17:00—19:00时段的交通流量数据进行预测,共900条数据,选择前14天的840条车流量数据作为训练数据,最后一天的60条数据作为预测数据。为了消除数据之间量纲的影响,将数据进行归一化处理,归一化方法如式(13)。预测方法采用小波神经网络(WNN)、人工蜂群算法优化的小波神经网络(ABC-WNN)和改进人工蜂群算法优化的小波神经网络(改进ABC-WNN)3种方法。相关研究表明,城市道路上某时刻的交通流量与该路段前几个时段交通流量有关,根据交通特性设计WNN结构,输入层为当前时间点前n个时间点交通流量,隐含层节点为Morlet小波基函数,输出层为当前时间点预测交通流量。本实验在MATLAB2014b环境下进行测试。 (13) 式中,x,y分别表示归一化前后数据,xmin表示样本中的最小值,xmax表示样本中的最大值。 (Ⅰ)采用WNN模型预测交通流量。输入层为4个节点,表示预测时间点的前4个时间点交通流量,由前4个时间点交通量预测该时间点交通量。经过多次测试,隐含层节点选择8个,输出层节点为1个,表示预测时间点的交通流量,则WNN结构为4-8-1。取学习速率为0.04,动量因子为0.6。设定WNN训练次数3 000次,用训练好的WNN进行预测。训练结果如图3所示,预测结果如图4所示。 图3 WNN训练结果Fig.3 Training results based on WNN 图4 WNN预测值与实际值比较Fig.4 Comparison ofthe predicted and actual values based on WNN (Ⅱ)采用ABC-WNN模型预测交通流,初始化参数,蜂群规模为40,则引领蜂、跟随蜂数量为20只,设定当某处蜜源经过20次循环迭代依然无法优化时便被放弃,ABC最大迭代循环次数为100次,目标函数为误差能量函数,适应度值为目标函数的倒数。将优化后的参数赋予WNN并训练300次。WNN参数同(Ⅰ)。训练结果如图5所示,预测结果如图6所示。 图5 ABC-WNN训练结果Fig.5 Training results based on ABC-WNN 图6 ABC-WNN预测值与实际值比较Fig.6 Comparison of predicted and actual values based on ABC-WNN (Ⅲ)采用改进ABC-WNN模型预测交通流,缩放因子F采用式(11)进行计算,取交叉概率为0.7,变异概率为0.02,将优化后的参数赋予WNN并训练300次。其他参数同(Ⅰ)和(Ⅱ)。训练结果如图7所示,预测结果如图8所示。 从图3~8可知,在训练过程中,WNN模型经过3 000次训练之后依然没有明显的收敛现象,而且训练的误差也比另外两种预测模型要大。ABC-WNN预测模型训练误差小于WNN模型,但由于ABC本身局部搜索能力较弱,因此出现了早熟现象。改进的ABC-WNN预测模型训练误差最小,与ABC-WNN模型相比有较强的跳出局部最优解能力。 图7 改进ABC-WNN训练情况Fig.7 Training results based on improved ABC-WNN 图8 改进ABC-WNN预测值与实际值比较Fig.8 Comparison of predicted and actual values based on improved ABC-WNN 根据预测值与实际值比较图来看,改进的ABC-WNN模型预测结果与实际值最为接近,表明改进的ABC-WNN预测模型能够较为准确地进行预测。 为了减少随机数对预测结果的影响,将3种预测模型进行10组测试,同时去掉每种模型两次最好预测结果和两次最差预测结果,取中间6组结果。分别计算预测结果的平均绝对误差、平均相对误差和均方差,其中,平均绝对误差计算公式如式(14)所示,平均相对误差公式如式(15)所示,均方差计算公式如式(16)所示。 (14) (15) 式中,EMRE表示平均相对误差。 (16) 式中,ERMSE表示均方差。 得出3种模型的预测结果如表1所示。 表1 3种预测模型误差比较Table 1 Error comparison among three kinds of prediction models 从3种模型预测结果可以看出,改进ABC-WNN算法预测结果的平均绝对误差、平均相对误差和均方差均明显优于其他两种预测模型,且与实际值接近。考虑到ABC-WNN预测模型的总体迭代次数远少于WNN模型,因此,可证明本文提出的预测模型有较快的收敛速度和较高的准确度。另外,ABC-WNN预测模型的预测结果也优于单一的WNN模型,说明组合优化模型比单一优化模型更有优势。 本文提出了基于改进人工蜂群算法优化小波神经网络预测模型,在ABC中引入DE算法的变异操作和遗传算法的选择交叉变异操作,并且在DE算法的变异操作中引入了自适应的缩放因子,增强了算法的多样性和跳出局部最优解的能力,保证算法全局搜索能力的同时,加强了算法在跟随蜂阶段的局部搜索能力。同时,选择、交叉和变异算子的加入进一步平衡了算法的全局探测能力和局部开采能力。再将优化后的参数用于小波神经网络中并对短时交通流量进行预测,获得了良好的预测效果。 本文所提出的预测模型在实验对比中体现了较快的收敛性和预测的准确性,但仍有进一步研究的空间,可以将Morlet小波函数替换为Marr小波函数或者Shannon小波函数,测试算法的收敛速度和准确性。另外,本文仅利用了历史交通流量值进行预测,没有考虑其他因素,事实上交通流的预测极其复杂,与多种因素有关,还需要研究更好的智能算法并考虑更多的实际因素来对交通流进行预测。 参考文献: [1]OKUTANI I,STEPHANEDES Y J.Dynamic prediction of traffic volume through Kalman filtering theory[J].Transportation Research Part B: Methodological,1984,18(1):1-11. [2]张晓利,陆化普.非参数回归方法在短时交通流预测中的应用[J].清华大学学报(自然科学版),2009,49(09):1471-1475. [3]廖荣华,兰时勇,刘正熙.基于混沌时间序列局域法的短时交通流预测[J].计算机技术与发展,2015,25(1):1-5. [4]BIDISHA G,BISWAJIT B,MARGARET O M.Bayesian time-series model for short-term traffic flow forecasting[J].Journal of Transportation Engineering,2007,133(3):180-189. [5]韩超.基于混沌理论的短时交通流预测方法[J].物流工程与管理,2012,34(4):116-117. [6]谢海红,戴许昊,齐远.短时交通流预测的改进K近邻算法[J].交通运输工程学报,2014,14(3):87-94. [7]LI S,SHEN Z,XIONG G.A k-nearest neighbor locally weighted regression method for short-term traffic flow forecasting[C]//2012 15thInternational IEEE Conference on Intelligent Transportation Systems[S.L.]:IEEE,2012: 1596-1601. [8]傅贵,韩国强,逯峰,等.基于支持向量机回归的短时交通流预测模型[J].华南理工大学学报(自然科学版),2013,41(9):71-76. [9]CHEN L,LI Q R,TIAN X Y,et al.Paratactic spatial-temporal two dimension data fusion based on support vector machines for traffic flow prediction of abnormal state[J].Advanced Materials Research,2012,532-533(6):1225-1229. [10]郑宣传,韩宝明,李得伟.基于RBF神经网络的城市快速路短时交通流预测研究[J].山东科学,2012,25(3):23-28. [11]杨显立,许伦辉,周勇,等.基于小波神经网络的道路交通流量实时预测模型研究[J].公路交通技术,2013(5):111-114. [12]KARABOGA D.An idea based on honey bee swarm for numerical optimization[EB/OL].[2017-06-02].https://doi.org/citeulike-article-id:6592152. [13]STORN R,PRICE K.Differential evolution-A simple and efficient adaptive scheme for global optimization over continuous space[J].Joural of Global Optimization,1997,11(4):341-359. [14]HOLLAND J H.Adaptation in natural and artificial systems[J].Quarterly Review of Biology,1975,6(2):126-137.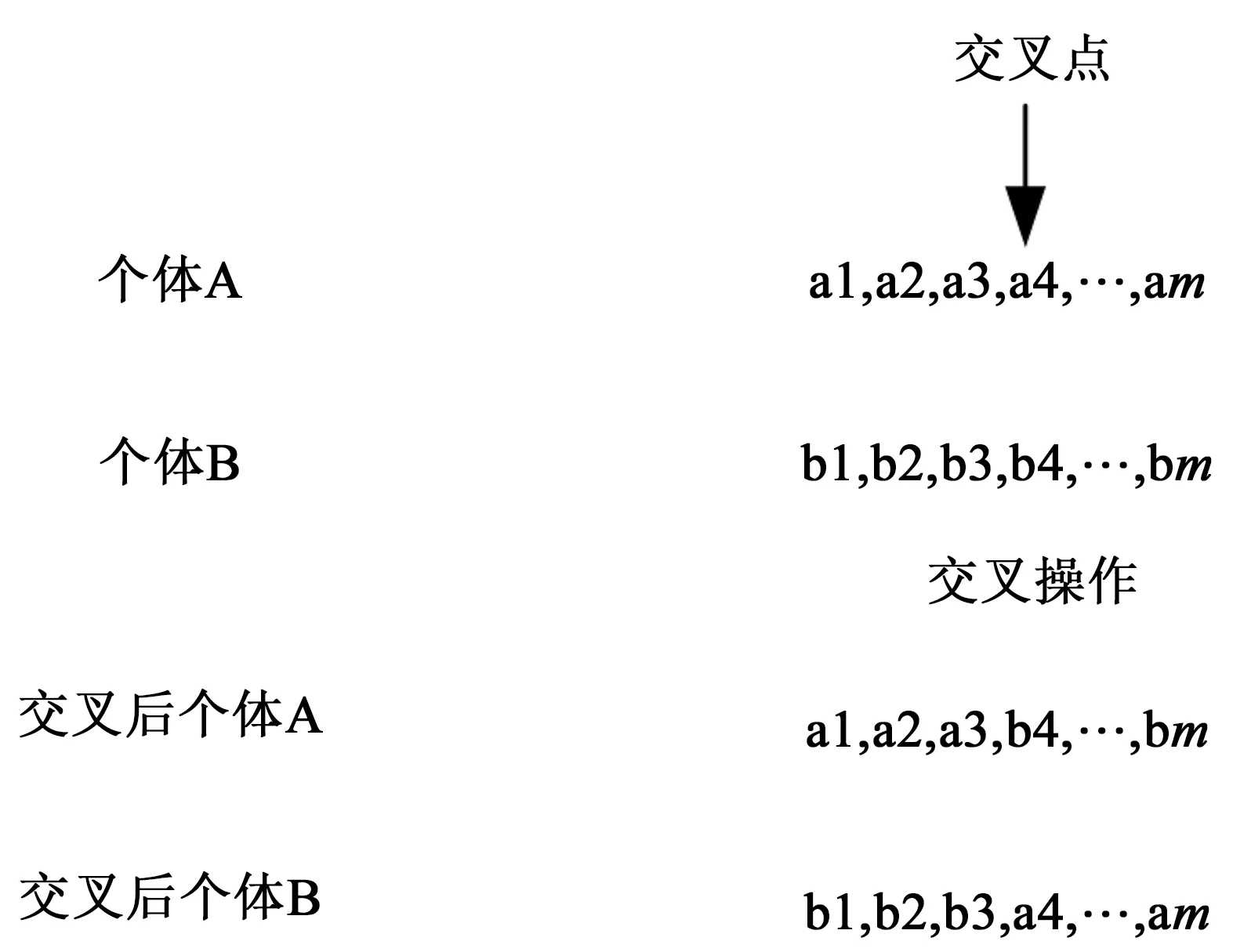
3.3 改进的人工蜂群算法优化小波神经网络步骤
4 仿真实验与结果分析
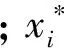
5 结论
