进化算法在大规模优化问题中的应用综述
2018-05-03瞿博阳岳彩通
梁 静, 刘 睿, 瞿博阳, 岳彩通
(1.郑州大学 电气工程学院,河南 郑州 450001;2.中原工学院 电子信息学院,河南 郑州 450007)
0 引言
当今很多优化问题已经从简单问题发展成为复杂问题.许多科学和工程应用问题都可以设计成大规模优化问题来进行求解,例如:大型电力系统、大量的资源调度问题、大规模交通网络的车辆路径规划等.然而随着优化问题越来越复杂,一些经典的算法已经不能满足实际需要.最近几年进化优化在许多实值和组合优化问题上取得了很大的成功,但是大多数的随机优化算法都会遭受“维数灾难”.因此,近些年学者们利用进化算法进行了多种有价值的尝试,并且针对大规模优化问题组织了专题会议,如Special Session on Evolutionary Computation for Large Scale Global Optimization,设计了新的测试函数、建立了相关的网站,并且在IEEE Transactions on Evolutionary Computation、Information Sciences、Soft Computing、Applied Soft Computing等优秀期刊也刊登了对于大规模问题的研究进展,显示出此研究领域的重要性.
1 数学表述
大规模优化问题可以用式(1)表述:
min/maxF(x)=f(x1,x2,…,xn),x∈X.
(1)
式中,X⊆n表示可行解集;n表示搜索空间的维数(即决策变量的个数);x=(x1,x2,…,xn)∈n表示决策变量;f:X→则表示一个从n维空间映射到一维适应度值F(x)的实值非连续性目标函数.在大规模设置中决策变量的个数n一般大于100[1],通常达到1 000维以上.
2 解决方法
在算法开始阶段,文献[2]给出了针对大规模问题的初始化方法,可以更加有效地寻找极点.而对于算法的主体部分,一般来说主流的策略可以分为两大类:协同进化策略和不分组策略.协同进化策略是由分治策略进化而来,主要思想是把大规模复杂问题分解成单变量或低维简单问题逐一解决;而不分组策略是运用一些特殊的策略或联合其他有效的算法来改进它们在解决大规模问题时的性能.
2.1 种群初始化方法
种群初始化方法主要包括以下5类:随机方法、定值设定法、两步式方法、混合方法和具体应用法.随机生成是最常用的方法,然而,在面对大规模优化问题(决策变量超过100)时,这种初始化方法效果不佳.文献[2]主要列出了一些不同初始化方法的对比研究.
在随机方法中,比较常用的是使用随机数产生器随机生成.而定值设定法则比较偏向于在搜索空间中产生均匀分布的点,在缺乏问题先验知识的情况下,一个比较均匀的种群可以促进算法在迭代早期的探索能力.近些年,两步式初始化方法在研究中较为常用,此方法分为前期产生初始点,后期根据条件改进这些点.混合方法一般来说是一些基础方法的组合.具体应用法则是指根据一些特殊的实值问题专门设计的初始化方法.文献[3]给出了现在常用的8种初始化方法(与DE算法相结合)的测试结果,使用的测试函数是CEC’2008[4].
2.2 不分组策略
学者们一般根据算法在不同阶段的特性设置不同的策略来解决低维问题,所以,针对大规模优化问题改进这些策略是一种比较常用的方法.
2.2.1 子代产生策略
一般来说,每种进化算法都有固定的子代产生策略.但是,对于大规模问题,使个体广泛分布在高维空间中比较困难.在每次迭代过程中,算法不断的收敛,因此下一代的学习策略很重要,不仅要向好的方向进化还要在搜索空间中广泛探索.文献[5]提出了反向学习策略,这种产生策略具有空间的导向性,可以增加种群的多样性,因此将其融入DE算法来解决大规模优化问题.文献[6]提出了基于广义反向学习的DE算法,该算法用广义反向学习方法(generalized opposition-based learning,GOBL)产生子代个体,用DE算法对产生的个体进行优化. 图1表示4个不同的广义反向学习的模型,其中,x是当前解,x*是反向解.

图1 4个不同的广义反向学习模型Fig.1 Four different GOBL models
图 1分别表示了文献[6]中所使用的4个GOBL模型,其中a表示搜索空间的下界,b表示搜索空间的上界,而GOBL-R模型是上述模型的一般表达式.当k=0时,是GOBL-SS模型;当k=1/2时,是GOBL-SI模型;当k=1时,是OBL模型.这些模型用于产生新个体并与原始个体混合进行选择.
2.2.2 新的变异策略
JADE是Zhang于2009年提出把变异策略和外部存档策略相结合的自适应方法[7].在无存档策略中,突变向量用式(2)产生:
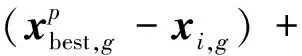
Fi·(xr1,g-xr2,g),
(2)
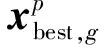
笔者在比较当前种群时,发现劣解可以为种群进化方向提供有用的信息.定义A为劣解归档集;P为当前种群;有存档的突变策略“DE/current-to-pbest/1”的突变向量用式(2)产生时,xr2,g是从P∪A中随机选择的个体.
文献[8]则给出了针对大规模全局优化的连续差分进化邻域搜索算法(sequential differential evolution enhanced by neighborhood search,SDENS),此算法主要分为两部分:①针对每个个体通过局部和全局邻域搜索策略产生两个实验个体;②从当前个体和两个新产生的实验个体中选取合适的一个作为新的当前个体.局部和全局邻域搜索策略在文献[8]中是一种突变策略.
一般来说,DE/target-to-best/1突变策略(如式(3)所示)主要着重于开发(exploitation),即所有的个体都会向同样的最优点Xbest移动,这样就造成算法收敛过快[9].Das等在文献[9]中改进了DE/target-to-best/1突变策略,提出了两个突变策略:局部邻域和全局邻域.
Vi,G=Xi,G+F·(Xbest,G-Xi,G)+
F·(Xr1,G-Xr2,G),
(3)
式中:Xbest,G表示在当前代G种群的最优位置;r1、r2∈{1,2,…,Np},且i≠r1≠r2.
局部邻域突变中最优位置是小邻域中的最优位置,不是全部种群的最优.改进后的模型表示如式(4):
Li,G=Xi,G+α·(Xn-besti,G-Xi,G)+
β·(Xp,G-Xq,G),
(4)
式中:下标n-besti,G表示Xi,G邻域的最优个体;邻域大小是k;p、q∈[i-k,i+k]且p≠q≠i.个体会向其相应邻域的最优点靠近,特殊点的吸引力减弱,这样就避免陷入局部最优.
全局邻域突变在原始DE/target-to-best/1突变策略中加上了α和β这两个比例因子,如式(5)所示:
Gi,G=Xi,G+α·(Xbest,G-Xi,G)+
β·(Xr1,G-Xr2,G).
(5)
针对这两个突变策略,文献[9]采用一个权重w∈(0,1)合并成一个新的突变策略,如式(6)所示:
Vi,G=w·Gi,G+(1-w)·Li,G.
(6)
2.2.3 自适应策略
自适应策略可以适应多种类型的测试函数集,对于全局优化的问题比较有效,但是此策略一般都局限在低维问题中.所以Yang在文献[10]中针对大规模优化问题对自适应策略进行了扩展,提供了更加广泛的参数自适应方案,提出了广义自适应差分进化算法(generalized adaptive DE, GaDE).一般的自适应策略可以被分为两类:基于启发式规则的和基于概率分布规则的.基于启发式规则的策略一般会引进一些新的参数,而且这些参数在某些情况下设置比较困难,JDE和DEGL算法就是用的此类策略.而SaDE、SaNSDE和JADE则属于基于概率分布的自适应方法.在这类算法中,不同的参数值是根据某一概率分布随机产生的,在进化操作和选择过程之后,好的参数值将作为下一次进化的分布规律被记录下来,用于产生更好的解.文献[10]中提出的自适应方式用的是第二类基于概率分布的策略.对于一个给定的进化算法,假设它有一个基于个体且非常敏感的参数A∈[Amin,Amax],同时此参数需要在进化过程中调整. 对于大规模优化问题,自适应策略不仅用在算法的参数调节上,在2.3节的分组策略中也有应用.
2.2.4 局部搜索策略
文献[11]把基于局部搜索的动态多种群粒子群优化算法(dynamic multi-swarm particle swarm optimizer with local search, DMS-L-PSO)扩展到大规模问题上,并取得了良好的效果.DMS-PSO是根据邻域结构把大种群分成很多小种群,这些小种群利用不同的重组策略被频繁重组,在频繁重组的过程中,种群不断交换它们之间的信息.而局部搜索策略是解决大规模优化问题的一种有效方法,主要加强算法的局部搜索能力.
把局部搜索策略加入DMS-PSO算法中:①每L代,根据小种群适应度值进行排序,利用准牛顿法根据局部最优解抽取小种群的前25%;②在搜索算法的结尾,利用准牛顿法更改当前的最优解.
2.2.5 新的进化策略
在解决大规模优化问题上,除了在原有的算法中加入新的策略,Cheng等也提出了一些新的群集智能算法用于解决此类问题.文献[12]提出了社会学习的粒子群优化算法(social learning particle swarm optimization algorithm, SL-PSO),不同于经典的粒子群优化算法(particle swarm optimization, PSO)利用历史信息(包括整个种群的最优位置global best和每个粒子的历史最优位置personal best)更新粒子,新算法则是粒子向当前种群中比它优秀的个体学习, 具体的学习方式如图 2所示.
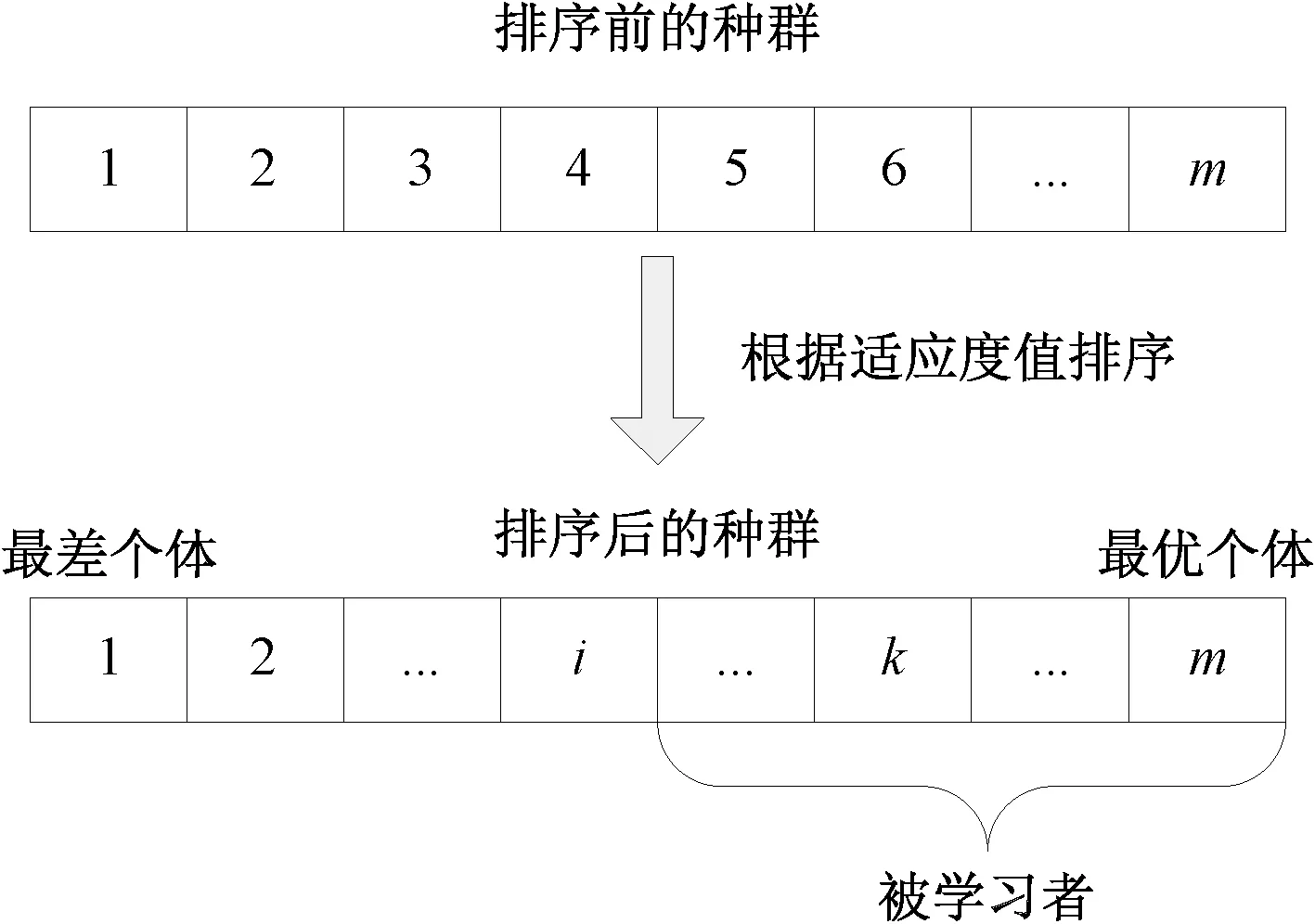
图2 SL-PSO的种群排序及学习行为Fig.2 Swarm sorting and behavior learning in SL-PSO
首先,对当前种群按适应度值排序,如果要更新第i个粒子,就向比第i个粒子好的个体(即图 2中的被学习者)和平均位置学习.而文献[13]则提出了竞争学习算法(competitive swarm optimizer,CSO),即随机从当前种群中抽取两个个体比较适应度值,失败者向胜利者学习,胜利者并不学习直接进入下一次循环,如图 3所示.
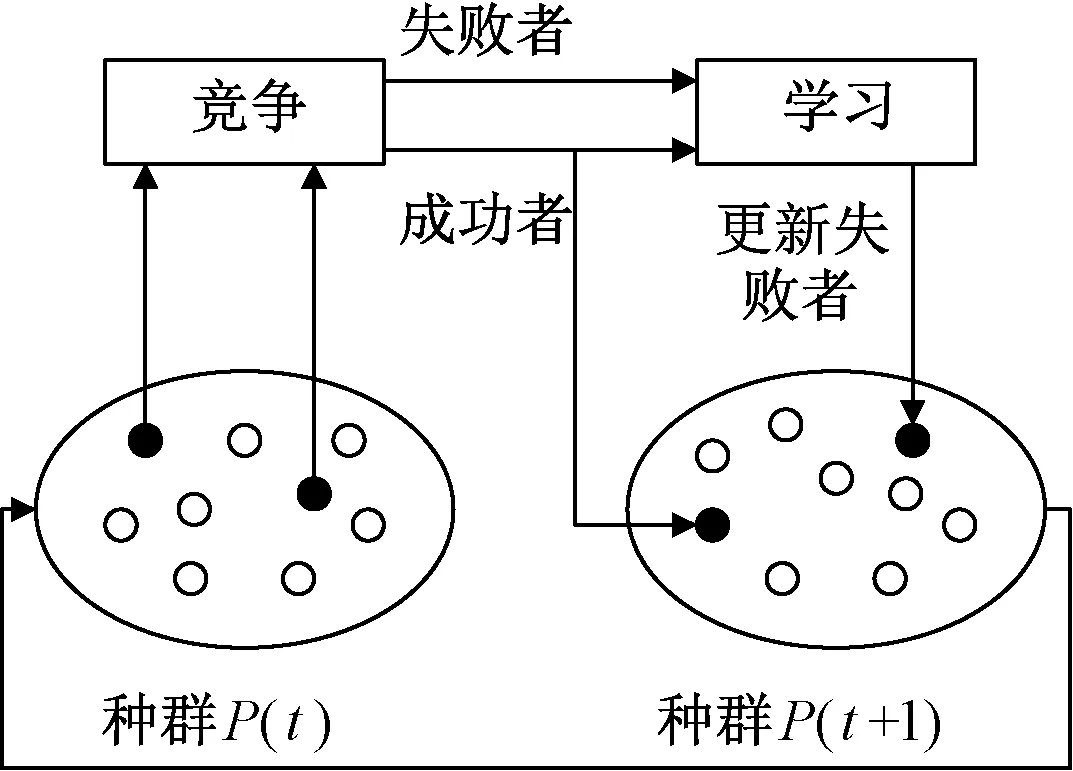
图3 CSO的一般构架Fig.3 The general idea of CSO
2.2.6 小种群搜索策略
文献[14]介绍了小种群搜索策略(minimum population search, MPS),这个策略主要是针对多模态问题.为了提高MPS在解决多模态问题时的性能,文献[15]使用了阈值收敛(threshold convergence, TC)方法来完成有序无偏的探索(exploration).MPS使用了相对较小的种群来提高可扩展性,种群越小,循环的代数越多,评价次数的利用率越高.如果种群大小n小于问题维数d,将其种群定义为n-1 维超平面.新解要严格按照所定义的超平面产生.在MPS中,每个种群成员用式(7)的方式初始化:
Sk= (rs1·bound/2,rs2·bound/2,…,
rsi·bound/2,…,rsn·bound/2),
(7)
式中:Sk是第k个粒子;rsi是介于-1到1之间的随机数;bound是维数上界.
阈值按式(8)更新:
min_stepi=α·diagonal·([FEs-k]/FEs)γ,
(8)
式中:α是主要空间对角线的分数;FEs是总评价次数;k是使用过的评价次数;γ是控制阈值衰减率的参数(注:max_stepi=2·min_stepi).
根据式(9)用父代产生子代:
triali=xi+Fi·(xi-xc)+Ostep_i·orth,
(9)
式中:xi和xc分别是父代中的个体及父代的中心点;Fi是范围为[-max_step,max_step]均匀分布的随机数.为了确保产生的新试探解在阈值范围之内,增加了正交算子.
在大规模优化问题中,由于增加了维数,MPS的种群也会增加,而这些增加的种群会使评价次数的有效利用率降低.为了增加这一利用率,MPS的种群大小将会动态减小如式(10)所示:
pop_sizet=init_pop·((FEs-k)/FEs).
(10)
2.3 分组策略
分组策略是指将原始的大规模问题分解成一系列小且简单的子问题,用分别优化独立子问题的方式解决.这种被称为分治策略最早是由Descartes在文献[16]中提出的,后来Potter在文献[17]中介绍了分组策略在大规模问题的求解方法,设计了协同进化(cooperative coevolution, CC)算法来改进标准遗传算法的性能.
协同进化策略在早期是静态分组的,分组并不会改变,但是这种方法在解决不可分或部分可分问题时主要依赖于在初始化时的分组情况,性能很不稳定,所以在改进该策略时使用动态分组方法,包括随机动态分组和学习动态分组.
2.3.1 基于静态分组的协同进化算法
Potter在文献[17]中提出了协同进化遗传算法(cooperative coevolutionary genetic algorithms, CCGAs),但是CCGA-1和CCGA-2只在最高为30维的问题中测试.2004年Frans 等在文献[18]中将该策略和粒子群优化算法(PSO)相结合,提出了CPSO-SK和CPSO-HK.CPSO-SK将维数分为K组,每组的维数是[n/K],用PSO算法对每组的维数进行更新.虽然CPSO-SK可以跳出次优解,但是在一些测试函数中收敛过快,为了使算法同时具有PSO的开发能力,CPSO-HK把这两种算法结合起来,一部分使用CPSO-SK算法,将CPSO-SK算法的最优解随机赋给用PSO优化的种群,条件满足时停止.
2.3.2 基于动态分组的协同进化算法
对于不可分问题来说,静态分组效率十分低.在不可分的测试函数中,决策变量存在着一些相互关系(正相关或负相关),如果把这些相互关联的决策变量一直分在一个组内,结果并不能收敛到最小.
2.3.2.1 随机动态分组
Yang于2008年在文献[19]中提出了新的协同进化(cooperative coevolution,CC)框架,同时还加上了自适应权重策略.其中,新的CC框架设计成动态改变群体结构,这种设计增加了相互关联决策变量分在一起优化的几率.此框架的主要思想是将n维的目标向量分成m个s维的子部分(假设n=m·s),使用EA算法对子部分进行优化;自适应权重策略则是将每个子部分都设置一个权重,用某一算子对权重进行优化.
文献[20]对文献[19]中的算法进行了改进,提出了新的多层协同进化算法(multilevel CC algorithm, MLCC),通过使用一个分解池来使分组的大小和目标函数联系的更加紧密. MLCC算法可以自适应选择合适的相互作用层次而不用考虑目标问题和优化阶段的特点;文献[7]介绍的JADE算法也使用了分组策略和权重优化的方法来寻找更加精确的解决方案.同时,这种解决方法可以加入其他的优化算法来改进它们在大规模优化问题中的性能.Li在文献[21]中同样将随机分组的协同进化策略与自适应权重用在PSO中,提出了CCPSO算法,并且于次年提出了CCPSO2算法,完善了CCPSO算法,使其在2 000维的问题中也有很好的性能.
2.3.2.2 基于学习的动态分组
虽然动态随机分组策略对于静态分组来说在解决决策变量相关性问题上比较有优势,但是决策变量的相关性并不能完全地区分出来.为了解决不可分问题并且减少决策变量之间的相互关联,Ray在2009年提出CCEA-AVP(自适应可变分区的协同进化算法,cooperative coevolutionary algorithm with adaptive variable partitioning).该算法的过程类似于标准的EA算法,首个M(一般设为5)次迭代包含所有的变量.在下一次迭代中,使用前50%的个体计算关联矩阵,并且将变量分成多个子种群.当变量之间的相关系数大于一个阈值时就被分到预先定义的一个子种群中,之后的每次迭代都把变量按其相关性分组.
文献[22]给出了辨识变量之间的相互关系的一个简单方法,“best”是目前的最优解;“new”是使用CC算法优化第i维后的最优个体;“rand”是随机从种群中选择的个体.根据这3个向量产生新的个体,如式(11)所示:
(11)
若f(x′)比f(x)的适应度值好,则维数i和j相互关联的概率增加.
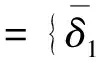
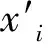
3 测试函数
为了对比算法的性能,一般用统一的测试函数来测试.文献[4]介绍了针对大规模优化问题的CEC’08专题会议函数测试集.CEC’10专题会议上的大规模优化算法测试集[4]则包含20个测试函数.为了更好地代表实际问题范围广泛的特性及对于基于分组的优化算法提供更加完备的测试,提出了CEC’13的测试函数集.与CEC’10的区别在于:CEC’10编写的不可分子部分的大小是均等的;而CEC’13则根据实际问题使不可分子部分的大小不均等,其相应变量的贡献度也会有所区分,并且不可分子部分也会有所覆盖,另外还具有病态、对称破裂及不规则等属性.CEC’13中包含了15个测试函数,这些测试函数均有平移和旋转特性.
4 算法对比
测试函数为CEC’08和CEC’10中的测试函数,主要测试的维数是1 000维,使用评价次数记录测试结果.在对比算法时保证最大评价次数相同,对算法的优化结果进行对比.
采用CEC’08测试集的主要有CODE、sep-CPM-ES、CSO、CCPSO、DECC-G、CDECC、MTS、CCPSO2、EPUS-PSO、DMS-PSO、MLCC.文献[21]中将算法CSO、CCPSO2、MLCC、sep-CMA-ES、EPUS-PSO、DMS-PSO进行了对比,并且采用了T检验方法对结果进行了统计.DMS-PSO可以准确地找出f1和f5的全局最优,其他5个函数的测试结果却没有CSO好.在与MLCC比较时,对于函数f4测试结果显示,MLCC明显优于CSO,而测试函数f4是shifted Rastrigin function,具有十分多的局部最优解,MLCC中针对每组的优化使用的是微分进化变异的方法.而CCPSO2的收敛性是这几个算法中最快的.sep-CMA-ES和EPUS-PSO在CEC’08的测试结果相比来说并不好.文献[21]同样是采用T检验来显示测试结果,因为CCPSO中含有一些用户自定义的参数,所以文献中对每个参数进行了测试,总的来说,除了函数f1、f2和f3,CCPSO2的性能要比DECC-G的好.文献[24]直接列出了CDECC和MTS在CEC’08上的测试结果,并使用Friedman检验了算法之间是否具有显著性差异,其置信度为0.05.测试结果表明CDECC在函数f6和f7中结果比较好,在f3、f4和f5没有MTS性能好,但是两者没有显著性差异.
使用CEC’10测试函数集主要有DECC-DG、MOFBVE、DECC-DML、DECC-G、DECC-D和MLCC等算法.文献[23]主要对比了DECC-DML、DECC-G、DECC-D和MLCC算法的测试结果,DECC-DML算法在20个测试函数结果中有14个函数的表现比DECC-G和DECC-D好,在与MLCC的比较中有12个函数的测试结果比较好,并且在文献[23]中使用多次运行的成功率来显示算法的性能.文献[25]主要是DECC-DG和MOFBVE的对比,MOFBVE算法的7个测试函数结果比DECC-DG优秀,但是在函数f11和f16中DECC-DG结果比较好.
5 结论
笔者主要总结了几个大规模优化的常用方法,解决大规模问题主要面临以下难点:搜索空间随着变量增加以指数形式扩大;问题的特性随着维数的增加变得更难,例如单峰问题可能会转变为多峰问题;算法在解决问题时花费的代价十分大;对于协同进化策略来说,变量之间是否可分是主要的问题.
(1)分组优化问题.协同进化策略是解决大规模问题的主要方法,但是,决策变量之间是否可分限制了协同进化策略计算,虽然使用学习的方式来判断是否可分,但是该方法的代价随着变量的增多而迅速加大.
(2)全部可分和全部不可分问题.在大多基准测试函数集中,都有全部可分或不可分问题,这些问题使用一般协同进化方法效果并不明显.对于全部可分问题,显然对每维单独优化比较好;但是对于不可分问题,变量的分组方式仍然是一个难题.
(3)不平衡的测试函数.在实际问题中,一般都会遇到子部分分布的不平衡特性,CEC’13大规模优化问题测试集中就针对该特性设计了测试函数.
(4)更加高维的问题.在上述算法中,测试任务一般是1 000维的,大规模优化方法可扩展性是未来研究工作的一个至关重要的要求.
参考文献:
[1] MAHDAVI S, SHIRI M E, RAHNAMAYAN S. Metaheuristics in large-scale global continues optimization: a survey [J]. Information sciences, 2015, 295: 407-428.
[2] RAHNAMAYAN S,TIZHOOSHH R, SALAM M M A. A novel population initialization method for accelevating evolutionary algorithms[J]. Computers & mathenmatics with applications, 2007,53(10):1605-1614.
[3] KAZIMIPOUR B, LI X, QIN A K. Initialization methods for large scale global optimization[C]//IEEE Congress on Evolutionary Computation. Cancun: Springer, 2013: 2750-2757.
[4] TANG K, YAO X, SUGANTHAN P N, et al. Benchmark functions for the CEC’2010 special session and competition on large scale global optimization[R]. Hefei: Nature inspired computation and applications laboratory, USTC, China, 2009.
[5] RAHNAMAYAN S, TIZHOOSH H R, SALAMA M M A. Quasi-oppositional differential evolution[C]//IEEE Congress on Evolutionary Computation. Tokyo: Springer, 2007:2229-2236.
[6] WANG H, WU Z, RAHNAMAYAN S. Enhanced opposition-based differential evolution for solving high-dimensional continuous optimization problems[J]. Soft computing, 2011, 15(11): 2127-2140.
[7] ZHANG J, SANDERSON A C. JADE: adaptive differential evolution with optional external archive[J]. IEEE transactions on evolutionary computation, 2009, 13(5):945-958.
[8] WANG H, WU Z, RAHNAMAYAN S, et al. Sequential DE enhanced by neighborhood search for large scale global optimization[C]//IEEE Congress on Evolutionary Computation. Shanghai: Springer, 2010: 1-7.
[9] DAS S, ABRAHAM A, CHAKRABORTY U K, et al. Differential evolution using a neighborhood-based mutation operator[J]. IEEE transactions on evolutionary computation, 2009, 13(3):526-553.
[10] YANG Z, TANG K, YAO X. Scalability of generalized adaptive differential evolution for large-scale continuous optimization[J]. Soft computing, 2011, 15(11):2141-2155.
[11] ZHAO S Z, LIANG J J, SUGANTHAN P N, et al. Dynamic multi-swarm particle swarm optimizer with local search for large scale global optimization[C]//IEEE Congress on Evolutionary Computation. Washington: Springer, 2008: 3845-3852.
[12] CHENG R, JIN Y. A social learning particle swarm optimization algorithm for scalable optimization[J]. Information sciences, 2015, 291(6):43-60.
[13] RAN C, JIN Y. A Competitive swarm optimizer for large scale optimization[J]. IEEE Transactions on Cybernetics, 2014, 45(2):191-204.
[14] BOLUFE R A, FIOL G S, CHEN S. A minimum population search hybrid for large scale global optimization[C]//IEEE Congress on Evolutionary Computation. Sendai: Springer, 2015: 1958-1965.
[15] MONTGOMERY J, CHEN S. A simple strategy for maintaining diversity and reducing crowding in differential evolution[C]//IEEE Congress on Evolutionary Computation. Vienna: Springer, 2012: 692-2699.
[16] DESCARTES R. Discourse on method[J]. Elizabeth haldane & g.r.t.ross the philosophical works of descartes, 1998, 10(1991):11-25.
[17] POTTER M A, JONG K A D. A cooperative coevolutionary approach to function optimization[C]//International Conference on Parallel Problem Solving from Nature. Berlin, Heidelberg: Springer, 1994: 249-257.
[18] FRANS V D B, ENGELBRECHT A P. A cooperative approach to particle swarm optimization[J]. IEEE transactions on evolutionary computation, 2004, 8(3):225-239.
[19] YANG Z, KE T, XIN Y. Large scale evolutionary optimization using cooperative coevolution [J]. Information sciences, 2008, 178(15):2985-2999.
[20] YANG Z, TANG K, YAO X. Multilevel cooperative coevolution for large scale optimization[C]//2008 IEEE Congress on Evolutionary Computation. Washington: Springer, 2008: 1663-1670.
[21] LI X, YAO X. Tackling high dimensional nonseparable optimization problems by cooperatively coevolving particle swarms[C]//2009 IEEE Congress on Evolutionary Computation. Vienna: Springer, 2009: 1546-1553.
[22] WEICKER K, WEICKER N. On the improvement of coevolutionary optimizers by learning variable interdependencies[C]//IEEE Congress on Evolutionary Computation. Washington: Springer, 1999(3):1627-1633.
[23] OMIDVAR M N, LI X, YAO X. Cooperative co-evolution with delta grouping for large scale non-separable function optimization[C]//IEEE Congress on Evolutionary Computation. Shanghai: Springer, 2010: 1-8.
[24] GE H, SUN L, YANG X, et al. Cooperative differential evolution with fast variable interdependence learning and cross-cluster mutation[J]. Applied soft computing, 2015, 36: 300-314.
[25] MAHDAVI S,RAHNAMAYAN S, SHIRIM E. Muctilevel framework for large-scale global optimization[J]. Soft computing, 2017,21(14):4111-4140.
