基于观测器的网络控制系统均方指数稳定控制器设计
2018-05-03刘艳红杨东伟
刘艳红, 杨东伟
(郑州大学 电气工程学院,河南 郑州 450001)
0 引言
网络控制系统是具有分布式结构的闭环控制系统,通过网络按照一定传输协议通讯.但是网络传输过程中普遍存在时延和数据丢包等现象,导致系统性能下降甚至不稳定.目前国内外研究人员针对网络控制系统的稳定性分析和控制问题开展了大量研究工作.文献[1-2]研究了马尔科夫跳变系统的稳定性,并给出了系统稳定的必要条件,设计了状态反馈控制器.文献[3-4]研究了具有传感器到控制器、控制器到执行器两类时延的网络控制系统的稳定性分析问题,采用Lyapunov方法给出了系统稳定的条件,但所采用的时延模型未能很好地刻画网络时延的特性.文献[5-7]利用变采样周期方法研究了包含传感器到控制器时延的网络控制系统问题,设计了状态反馈控制器,但计算量较大且没有考虑控制器的实现问题,难以应用于实际网络控制系统.文献[8]研究了一类具有随机网络诱导时延的控制系统H∞滤波器问题,但是未考虑传感器到控制器随机采样时延.文献[9]针对线性时变网络控制系统,通过将系统离散化设计了稀疏状态观测器,并分析了系统的稳定.文献[10]针对随机时延采用时延预测补偿的方式提高系统对参考输入信号的跟随性能,但对稳定控制问题没有进行研究.
本文研究基于状态观测器的网络控制系统的均方指数稳定控制问题.首先通过变采样周期将系统转化为离散化系统,并将传感器到控制器的时延建模为马尔科夫过程,较为准确地描述了网络时延的特性;然后设计了基于观测器的反馈控制器,分析了闭环系统的均方指数稳定性;最后利用Schur补引理将观测器和控制器设计转换为线性矩阵不等式的求解问题,给出了反馈控制增益及观测器增益的求解方法.数值算例和网络环境下车摆系统的均方指数稳定控制仿真结果验证了笔者所提出的控制器设计方法的有效性.
1 问题描述
图1所示为单边双通道网络控制系统.
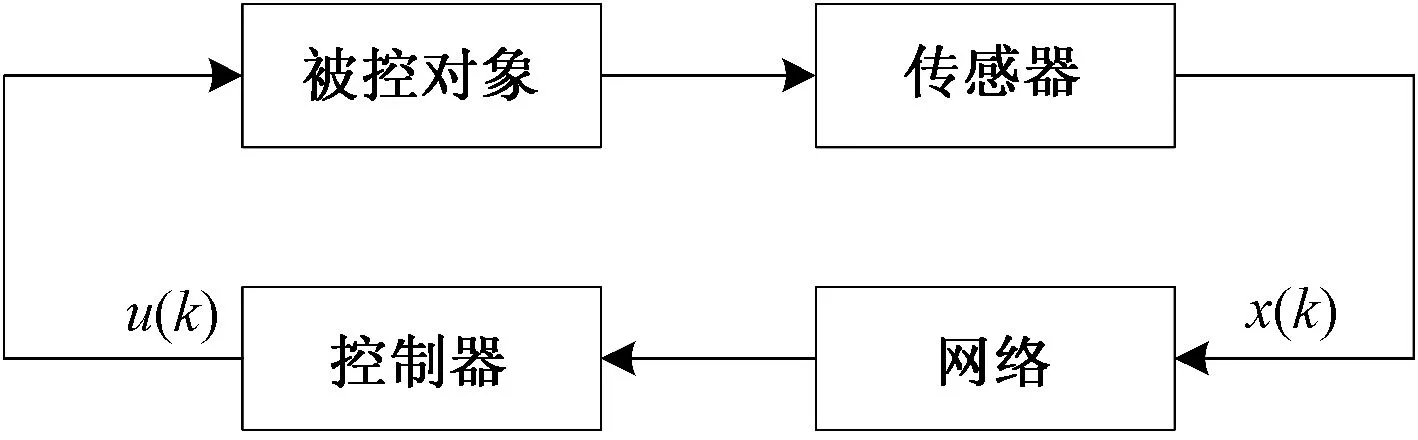
图1 网络控制系统结构Fig.1 Structure of network control system
系统满足以下条件[11]:
(1)控制器、执行器与被控对象之间以及传感器与被控对象之间采取直接连接方式,无网络诱导时延.
(2)传感器与控制器之间采用网络连接方式,网络时滞仅仅存在于传感器与控制器之间.
被控对象的动态模型为:

(1)
式中:x(t)∈n为系统状态;u(t)∈m为控制输入;y(t)∈c为系统输出.
对系统进行变采样周期采样,采样周期由网络时延决定,即Tk=dk,将传感器到控制器的时延dk∈(τ1,τ2,τ3,…,τn)建模为马尔科夫链,其转移概率矩阵满足:

(2)
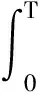
由于系统状态不易直接测量,考虑如下基于状态观测器的反馈控制:
(3)
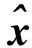
ek(k+1)=A(Tk)ek(k)-FkCek(k).
(4)
定义增广状态向量z(k)=[xT(k)eT(k)]T,则闭环系统可以表示为:
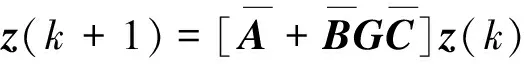
(5)
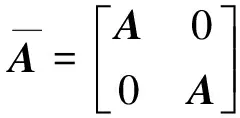
本文的目的是设计基于观测器的反馈控制器,使得闭环系统均方指数稳定,即存在α∈(0,1)和β>1,使得系统满足[12]:
E{‖z(k)‖2}<βαk‖z(0)‖2.
(6)
2 控制器增益与稳定性分析
定理1如果存在矩阵P(τi)=PT(τi)>0满足:
P(τr)<0,τr∈dk,
(7)
则闭环系统(5)均方指数稳定.
证明选择Lyapunov函数
V(z(k))=zT(k)P(τr)z(k),
(8)
则
E{ΔV(k),k}=E{zT(k+1)P(τr)z(k+1)|x(k)}-
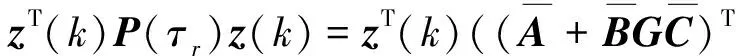

(9)
由条件(7)可得E{ΔV(k),k}<0,故存在0 E(V(z(k+1)),k+1) E(V(z(1),1) ⋮ E(V(z(k),k) 选择α=max{a1,…,ak},则有 E(V(z(k)),k) (10) 此外,注意到: λminP(i)zT(k)z(k)≤zT(k)P(i)z(k)≤ λmaxP(i)zT(k)z(k), (11) 有 E(‖z(k)‖2))<βαk‖z(0)‖2. (12) 下面通过Schur补引理[13]将反馈增益的求解问题转化为线性矩阵不等式的求解问题. 定理2如果存在适当维数的矩阵 N∈n×n,Y∈m×n, 使得 (13) P(τr)∈n×n,D∈n2×n2, J(τr)∈n2×n,, D=diag{P-1(τ1),P-1(τ2),…,P-1(τn)}. 证明式(13)左右两边分别乘以[J(τr),I]和[J(τr),I]T,可得 (14) 根据Schur补引理,有 (15) 从而有 JT(τr)D-1J(τr)-P(τr)<0. (16) 将 D=diag{P-1(τ1),P-1(τ2),…,P-1(τn)} 代入式(16),可得 根据定理1可知闭环系统均方指数稳定. 考虑下面网络控制系统: 离散化系统动态方程参数为: 根据定理2,通过求解线性矩阵不等式可得控制器和观测器增益分别为: 图2 基于本文控制器的状态响应曲线Fig.2 State response under the proposed controller in this paper 图3 基于固定采样周期方法的状态响应曲线Fig.3 State response under constant sampling method 图4 状态观测器误差响应曲线Fig.4 Response of the state observer error 笔者忽略小车所受的摩擦力且不计空气阻力,网络环境下车摆系统的动态控制方程可以表示为[15]: 图5 控制输入曲线Fig.5 Response of the control input 根据定理2,可得使得系统均方指数稳定的反馈控制器和观测器增益分别为: 仿真结果如图6~10所示. 从仿真结果可以看出,采用本文方法设计的控制策略能够使车摆系统在受到传感器到控制器随机网络时延时避免出现大幅度震荡,系统状态均能够快速收敛到平衡状态, 验证了控制器方案的有效性. 图6 小车响应曲线Fig.6 Response of the state of the vehicle 图7 倒立摆响应曲线Fig.7 Response of the state of the inverted pendulum 图8 状态观测器误差响应曲线Fig.8 Response of the state observer error 图9 状态观测器误差响应曲线Fig.9 Response of the state observer error 图10 控制输入曲线Fig.10 Response of the control input 笔者对基于状态观测器的网络控制系统均方指数稳定控制问题进行研究.首先采用变周期采样将系统离散化并建模为马尔科夫跳变系统;然后设计了状态观测器和反馈控制器,证明了闭环系统的稳定性;最后采用Schur补引理把观测器和控制器增益矩阵的求解问题转化为线性矩阵不等式的求解问题.仿真结果验证了笔者所提控制方案的有效性. 参考文献: [1] XIAO N, XIE L H, FU M Y. Stabilization of markov jump linear systems using quantized state feedback[J]. Automatica, 2010, 64(10): 1696-1702. [2] 赵立英, 窦立亚, 刘贺平. 具有时变时滞的变采样周期网络控制系统的稳定性分析[J]. 北京科技大学学报, 2014, 36(8): 1123-1127. [3] SHI Y, YU B. Output feedback stabilization of networked control systems with random delays modeled by Markov chains[J]. IEEE transactions on automatic control, 2009, 54(7): 1668-1674. [4] JI M M, LI Z J, YANG B, et al. Stabilization of markov jump linear systems with input quantization [J]. Circuits, systems, and signal processing, 2015, 34(7): 2109-2126. [5] 于水情, 李俊民. 变采样周期网络控制系统的量化状态反馈控制[J]. 北京理工大学学报, 2011, 31(7): 814- 817. [6] CLOOSTERMAN M B G, HETEL L, WOUW N V D, et al. Controller synthesis for networked control systems[J]. Automatica, 2010, 46(10): 1584-1594. [7] TRUONG D Q, AHN K K. Robust variable sampling period control for networked control systems[J]. IEEE transactions on industrial electronics, 2015, 62(9): 5630-5643. [8] 张端金, 刘雪, 范鑫. 基于Delta算子时变时延网络控制系统的H∞滤波[J]. 郑州大学学报(工学版), 2016, 37(2): 10-14. [9] RAZEGHI-JAHROMI M, SEYEDI A. Stabilization of networked control systems with sparse observer controller networks[J]. IEEE transactions on automatic control, 2015, 60(6): 1686-1691. [10] 刘艳红, 罗永平, 刘言兴. 基于改进型JGPC的网络系统随机时延补偿[J]. 郑州大学学报(工学版), 2014, 35(1): 30-33. [11] 王欣, 康宇, 尚伟科. 一类基于双通道网络的离散Markov跳跃系统的鲁棒控制[J]. 中国科学技术大学学报, 2013, 43(4): 278-286. [12] XU Y, SU H Y, PAN Y J. Output feedback stabilization for markov-based nonuniformly sampled-data networked control systems[J]. Systems & control letters, 2013, 62(8): 656-663. [13] XIONG J L, LAM J. Stabilization of linear systems over networks with bounded packet loss[J]. Automatica, 2007, 43(1): 80-87. [14] 邢伟, 孙阳, 戴良萃. 基于观测器的时延网络控制系统稳定性[J]. 东北大学学报(自然学科版), 2014, 35(4): 457-465. [15] 桑英军,范媛媛,徐才千.单级倒立摆控制方研究[J]. 控制工程, 2010, 17(6): 743-745.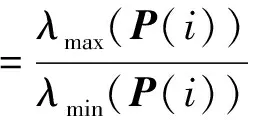
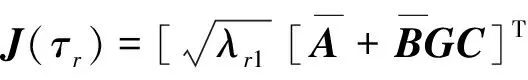


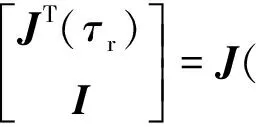
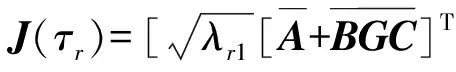
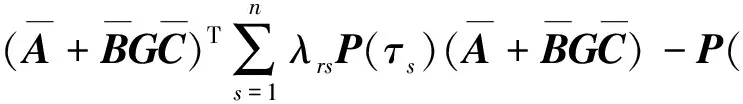
3 仿真
3.1 数值算例


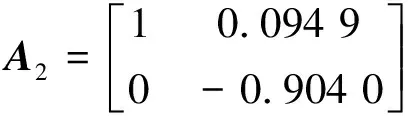
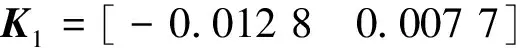
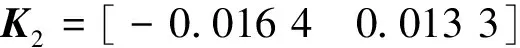
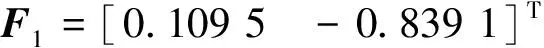

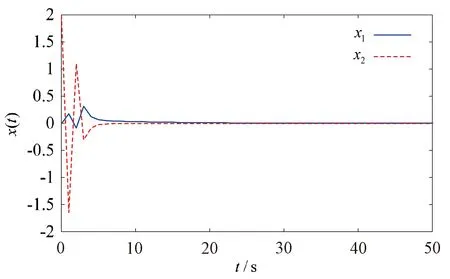
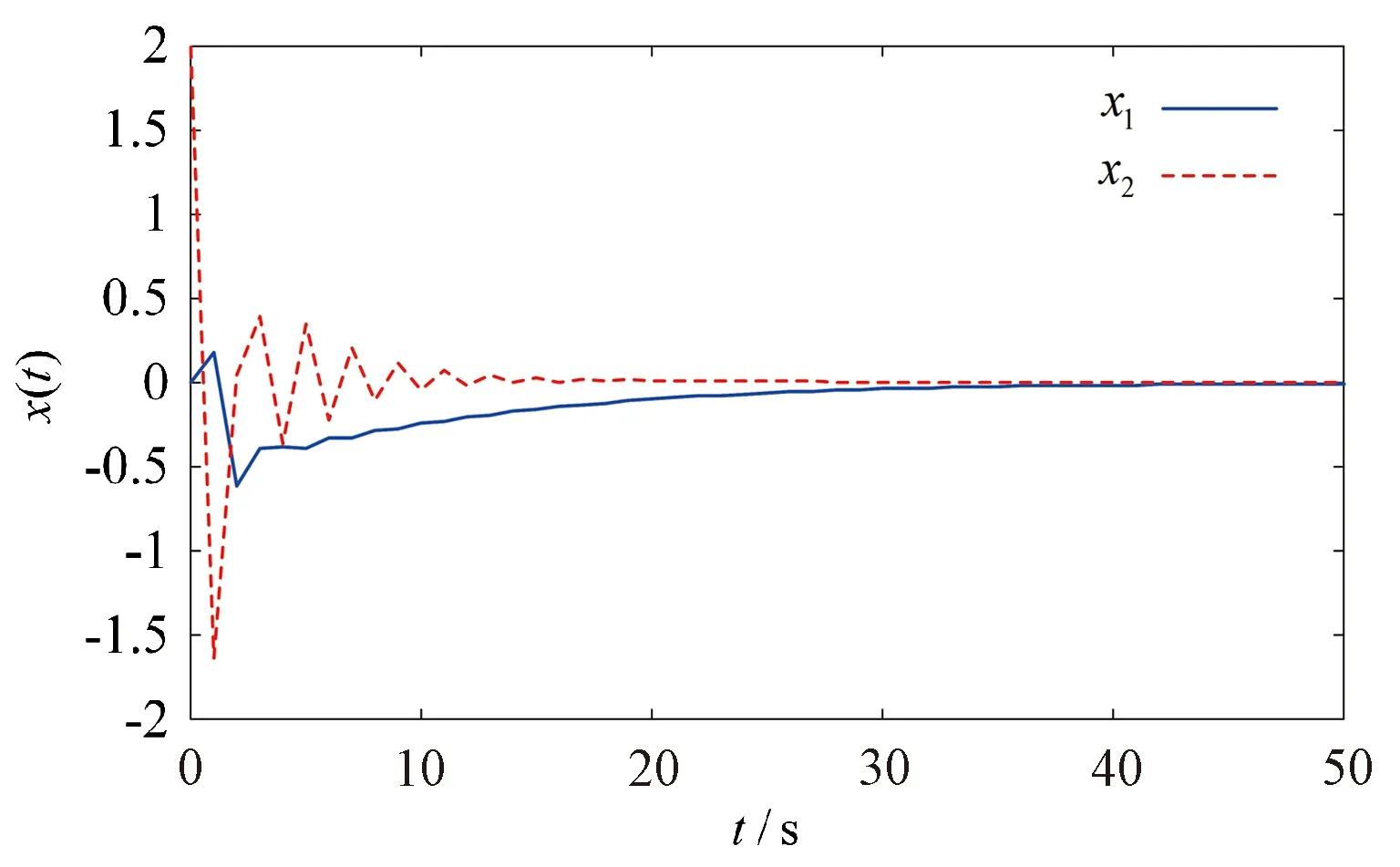

3.2 网络环境下车摆系统稳定控制
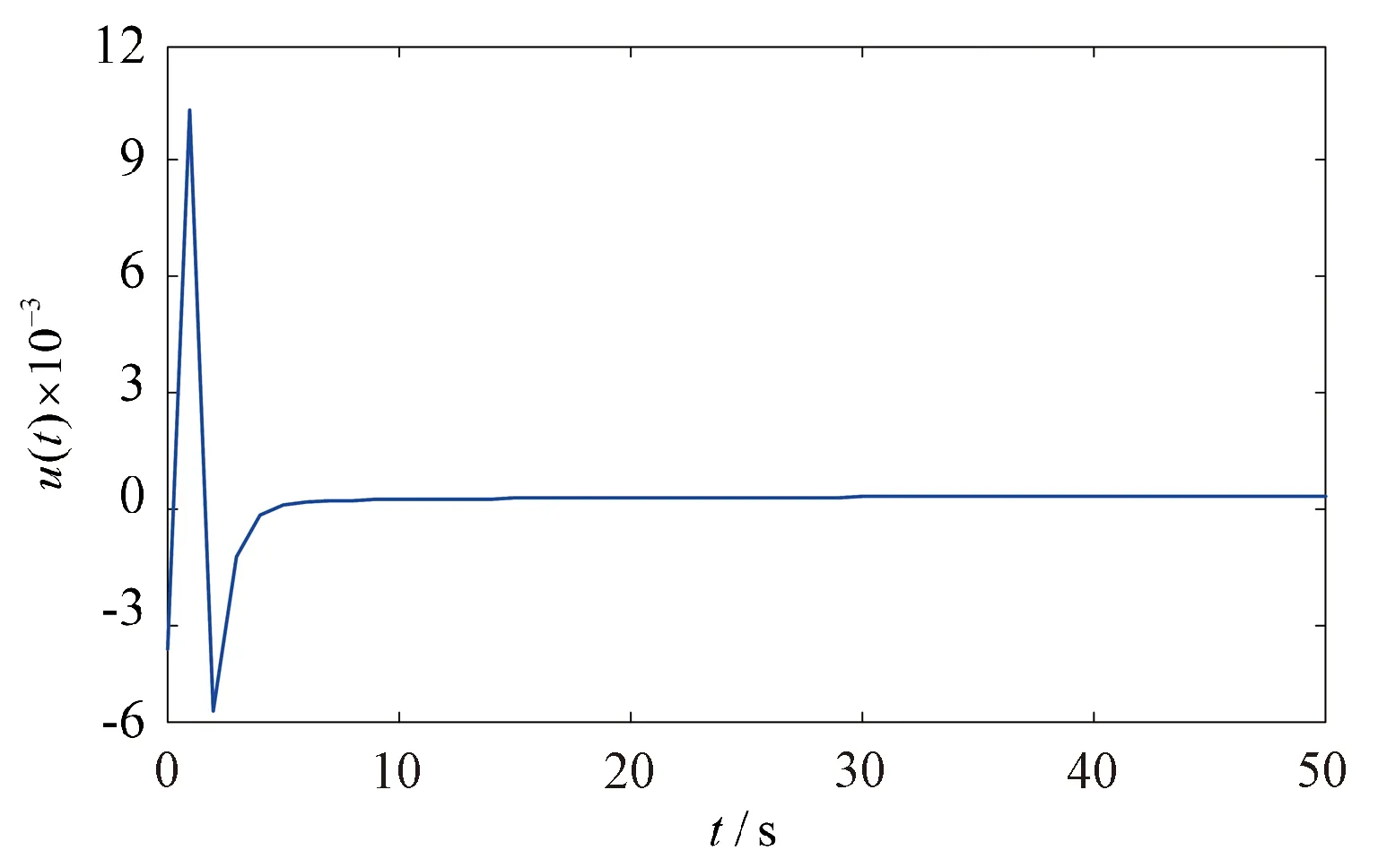

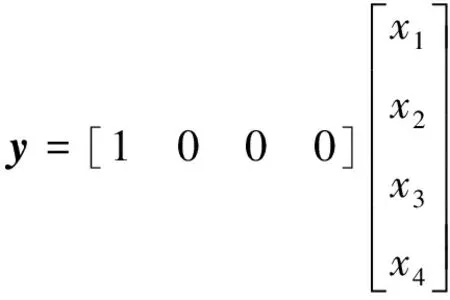
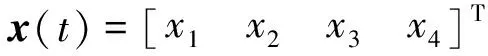





4 结论
