智能船舶传感器间歇性故障容错滤波算法*

周志杰 徐海祥 冯 辉

(武汉理工大学高性能船舶技术教育部重点实验室1) 武汉 430063) (武汉理工大学交通学院2) 武汉 430063)

0 引 言

近年来，随着船舶智能化发展，智能船舶技术领域激发了国内外诸多学者强烈的研究兴趣[1-2].智能航行应具有在开阔水域自主航行功能，即船舶根据传感器测量得到的自身位置信息以及周围环境信息，通过控制算法实现船舶的自主航行[3].因此，智能船舶的智能化程度与自主控制精度取决于传感器获取的数据的精确度.然而，由于海上环境变化的不确定性，传感器与传感器、传感器与其他设备之间存在相互干扰等因素，造成传感器测量数据的失真，加上不确定性噪声的干扰，降低了传感器获得的数据的可信度，甚至出现不可忽略的偏差.为解决不确定干扰带来的问题，先后有多种滤波方法被设计和使用，例如均值滤波、中值滤波、滑动多项式滤波、α-β-γ滤波、3σ滤波、Kalman滤波、线性滤波和无迹滤波等[4].尽管在理论上可以证明上述滤波方法的可行性，然而若要应用于工程实践中却往往有较大的局限性，例如Kalman滤波和无迹滤波对滤波模型精度要求较高，而实际工程中无法建立精确的滤波模型，且其不具有良好的抗干扰能力；均值滤波和中值滤波虽然无需建立滤波模型，但是这类滤波方法为平滑处理，即窗口滤波估计的结果为窗口中央的数值，而非当前时刻下滤波处理后的传感器数据，因此会产生数据延时，对于智能船舶的自主控制尤为不利；线性滤波，又称最小二乘滤波，是基于最小二乘的思想估计出当前时刻的数值，因此具有一定的抗干扰能力，在工程实际应用中较为常见，然而，该方法在测量数据变化较快的情况下滤波效果较差；3σ法需要足够数量的数据方可判断是否为野值，这样不仅降低了系统的实时性，同时增加了数据的存储量，进而增大了数据处理的复杂度.由于滤波器的滤波效果对数据质量的依赖性较大，当测量数据带有信噪比低、有野值、随机误差非平稳等情况时，传统滤波器的滤波效果会受到明显影响，甚至会偏离测量对象真实变化情况，导致滤波结果失真[5-6].近年来，为解决上述问题，一方面，部分学者对传统滤波器加以改进，以增强其容错性：曾静等[7]采用四阶自回归模型进行残差序列的预测与故障检测，并结合卡尔曼滤波设计出一种基于有限记忆在线预测的卡尔曼容错滤波器；为解决GPS量测输出信息中常含有故障信号的问题，石静等[8]提出了一种鲁棒容错滤波算法，将GPS量测输出中可能含有的故障信号扩充为系统的状态，通过鲁棒滤波算法在线实时进行估计，并对系统进行补偿，达到容错的目的；耿峰等[9]提出了一种多模式联邦高斯和粒子容错滤波技术，以提高组合导航系统的鲁棒性；Geng等[10]设计了一种带故障检测功能的容错卡尔曼滤波器(fault-tolerant-kalman-filter,FTKF)，在雷达产生错误时自动检测出故障信号并对数据进行滤波处理，试验证明可以达到预期的容错效果.另一方面，部分学者通过改变滤波器结构增加其容错性能：雷江涛[11]通过比较四种联邦滤波器的结构后指出无复位联邦滤波模式具有良好的容错性能；张崇猛等[12]设计了一种基于极大似然准则自适应滤波的无重置联邦滤波器，提高了舰船导航系统的稳定性和精度.对于智能船舶导航系统中传感器出现间歇性故障的情况，大部分学者倾向于使用联邦滤波结构，联邦滤波结构虽然有比较好的容错性能，但其对系统的冗余度有较高要求，并且当较多传感器出现故障时，例如智能船舶进入强磁强电波干扰环境中致使所有电磁传感器出现间歇性故障，联邦结构将不具备较为理想的容错性能.在航空领域，胡绍林等[13]提出了一种Q滤波(Quartile Filter)算法，引入四分法取样的基本思想，对滑动窗口中的数据进行四分法取样，计算四分位均值算子，并进行残差补偿，这种方法虽然有较好的滤波效果，但其存在与中值滤波和均值滤波相同的延时问题，不适用于对数据实时性要求较高的智能船舶应用之中.

本文将上述Q滤波算法引入到智能船舶应用中，并对Q滤波算法进行改进，将变窗口长度、线性估计理论与Q滤波算法相结合，在保证容错性能的同时，增强其实时性.

1 船舶运动学模型建立

为便于仿真实验，需建立船舶运动数学模型.船舶运动具有6个方向的自由度：纵荡、横荡、垂荡、横摇、纵摇和首摇.一般情况下，建立船舶平面运动数学模型，仅考虑纵荡、横荡和首摇3个自由度即可.图1为船舶平面运动坐标系.

图1 船舶运动坐标系

图中：XOY为大地坐标系；xoy为随船坐标系.

设船舶受外界小扰动时，纵向速度不变，其运动方程为

(1)

(2)

式中：m为船体质量；my，mx为船体附加质量；u0为横向速度；ω为首向速度；Izz为绕Z轴的转动惯量；Jzz为船体附加惯性矩；δ为舵角；Yv，Yr，Yδ，Nv，Nr，Nδ为水动力导数.

对于水面船舶的操纵运动，我们最关心的是首向角Ψ和角速度ω随时间变化的规律，即二阶操纵运动方程为

(3)

式中：

(NrYv+Nv(mU-Yr))

(NrYv+Nv(mU-Yr))

K=(YδNv-NδYv)/(NrYv+Nv(mU-Yr))

其中：U为船舶纵向速度.

对于一般船舶，由于操舵速度有限，且船舶本身的惯性很大，对舵的响应基本上是一种缓慢的运动，所以上式可以近似写为一阶形式，即

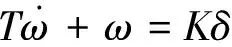
(4)

式(4)即为K-T方程.选取上述方程作为算法仿真研究采用的船舶运动学模型，其中K，T系数根据具体船舶的操纵性能指数而定.

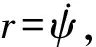
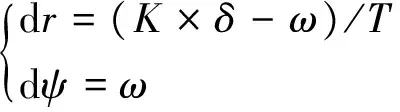
(5)

通过解微分方程组(5)，可得到运动角速度随时间变化的函数，即可用于推算船舶运动位置信息.

2 容错滤波算法设计

对于传感器动态测量的数据，可以将其“加性”分解，即

y(tk)=s(tk)+ε(tk)+σ(tk)

(6)

式中：y(tk)为传感器测量的数据值；s(tk)为绝对真值；ε(tk)为噪声干扰项；σ(tk)为随机野值.由上式可知，传感器测量得到的数据与绝对真值存在两项误差：具有恒定均值的噪声项与具有极大不确定性的野值项.理论上，只要剔除野值并滤除噪声项即可使传感器测量得到的数据无限趋近于真值，然而困难的是如何诊断一个数据是否为野值.由于野值的产生源于传感器的间接性故障如丢包、暂时性卡死等，故而野值的大小一般明显偏离噪声值.根据这一特点，可以采用四分法取样的基本思想，去除偏大和偏小的数据，取中值附近的50%的数据为可信度较高的不带野值的数据序列.

在航空领域，胡邵林等基于上述思想提出一种针对动态测量数据的Q容错滤波算法，算法流程为

1) 选择适当的窗宽半径H的滑动时间窗口[tk-H,tk+H]内的测量数据片段Sk={y(tk),tk∈[tk-H,tk+H]}进行四分位均值算子的计算：

(7)

式中：nk为数据片段Sk的数据点个数；Q(Sk，nk)为四分位均值算子，即将获得的数据序列Sk进行从小到大排序，取中值左右各25%nk的数据序列计算其均值.

3) 将残差序列ε(tk)进行四分位滤波

(8)

4) 将两次四分位滤波的结果进行线性组合，获得tk时刻的估计值

(9)

以上过程为Q滤波算法，虽然上述算法具有一定的容错性，但由于该算法用于对测量数据进行平滑处理，由1)可知，该算法的滤波对象为以某一个时刻的数据y(tk)为中心的数据片段，然而在实际应用中，传感器无法获取当前时刻tk之后的数据，因此无法根据上述算法获得当前时刻数据的估计值.如果将窗口前移半个窗口的长度，则Q滤波算法得到的为tk-H/2时刻的数据，若将其当作当前时刻的数据，将会导致数据延时，降低滤波算法的实时性.

针对上述问题，对Q滤波算法进行改进，改进后的算法流程为

1) 选择合适的初始滑动窗口长度ζ，取一段测量数据序列S(tk).

S(tk)={y(tk-ζ+1),y(tk-ζ+2),…,y(tk)}

(10)

2) 将获得的数据序列进行从小到大排序，取中值左右各25%ζ的数据序列计算其均值Q(tk).

3) 计算序列S(tk)各项与均值的偏差，获得残差序列ε(tk).

ε(tk)={y(tk-ζ+1)-Q(tk),

y(tk-ζ+2)-Q(tk)，…，y(tk)-Q(tk)} (11)

4) 将残差序列重复过程2)，计算残差均值，作为残差补偿P(tk).

5) 将2)计算的均值与残差补偿相加，作为参考值.

(12)

其中：

6) 取后半部分长度为τ的数据段η(tk)，重复过程2)至5)，求得后半段参考值.

η(tk)={y(tk-τ+1),y(tk-τ+2),…,y(tk)}

(13)

其中：

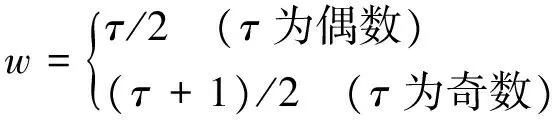
7) 通过求得的两个参考值线性估计出y(tk)的估计值s(tk).

s(tk)=y(tk-τ)+(y(tk-w)-y(tk-τ))/

(τ-w)×τ×CS

(14)

式中：CS为修正系数，其大小与选取的初始窗口长度和数据变化率相关，通常情况下取CS的值为1.

改进的算法在原Q滤波算法的基础上，将窗口前移了半个窗口长度，并对窗口后半段数据再一次进行了Q滤波计算，并通过线性估计的方法求得当前时刻的数据y(tk)的估计值.

在滤波精度、克服数据迟滞效应及实时性等方面，改进的Q滤波算法较原Q滤波算法均有所提升：

1) 在滤波精度方面，由于原Q滤波算法主要用于数据的平滑处理，因此仅需通过筛选出置信度较高的数据片段获取可以表征数据变化情况的数即可；而改进的Q滤波算法在原Q滤波算法的基础上，通过对窗口后半段数据进行估值，获取窗口数据的变化趋势，以期估计当前时刻的数据.因此，改进的Q滤波算法具有更高的滤波精度.

2) 在克服数据迟滞方面，原Q滤波算法主要用来估计出窗口中央的数值，即在tk时刻原Q滤波算法获取的为tk-ζ/2(ζ为滤波窗口长度，下同)时刻的数据的滤波值，从而达到数据平滑的目的.如果将其直接应用于对当前时刻的数值进行估计，则必定会产生迟滞效应.而改进的Q滤波算法可以通过获取窗口数据的变化趋势，获取tk时刻的滤波值.因此改进的Q滤波算法有效克服了数据的估计延迟问题.

3) 在实时性方面，原Q滤波算法为估计出当前时刻的滤波值，需要通过滑动窗口进行ζ/2次四分位均值算子的计算；而改进的Q滤波算法仅需进行两次四分位均值算子得计算即可获取当前时刻的滤波值.当窗口长度越长，原Q滤波算法耗时越长，而改进的Q滤波算法的耗时几乎不发生变化.因此，改进Q滤波算法有更好的实时性.

综合上述，该算法不仅保留了原Q滤波算法的容错性能，而且在滤波精度、克服迟滞效应及实时性等方面均较原Q滤波算法优良.

3 实验仿真与结果分析

为验证本文提出的改进算法的可行性，本文分别对智能船舶低速直航和低速回转运动下传感器获取的信息进行处理，并与原Q滤波算法和目前实际工程中应用较为广泛的线性拟合滤波方法进行对比.

仿真实验基于MATLAB平台.仿真中采用文献[14]中的无人艇作为仿真对象，选取0.14 m吃水、1.2 kn航速、15°舵角时的K，T指数作为本文仿真采用的参数，即K=1.1，T=0.17.

3.1 直航工况下的仿真对比

假定船舶从原点出发，以1 m/s的航速沿60°方向直线航行.在不存在任何噪声干扰情况下，船舶理想运动情况见图2.

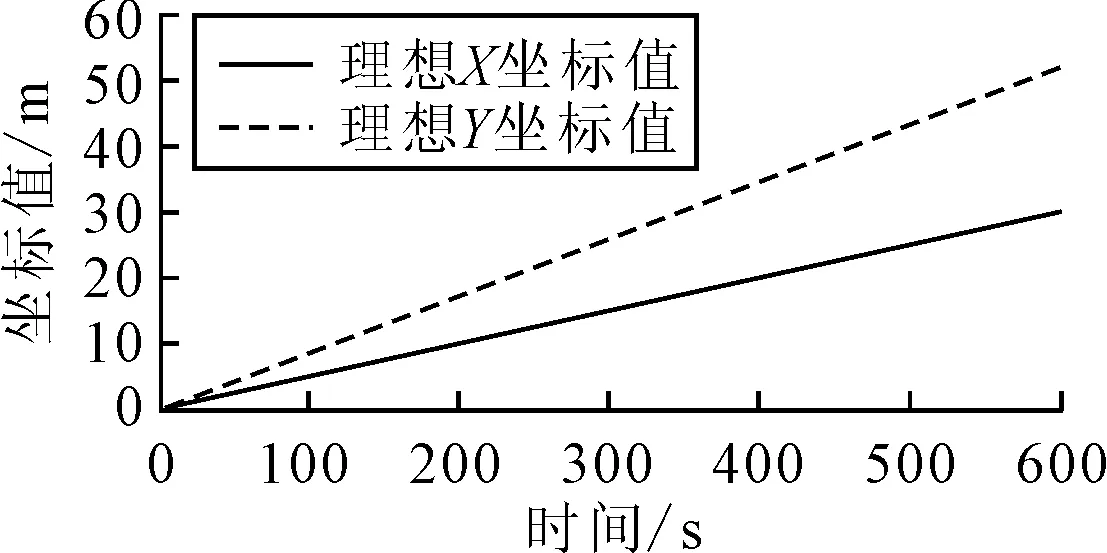
图2 理想情况下船舶位置测量值

真实情况下，传感器测量带有一定的量测噪声，且当传感器发生间歇性故障时，带有故障信息见图3.

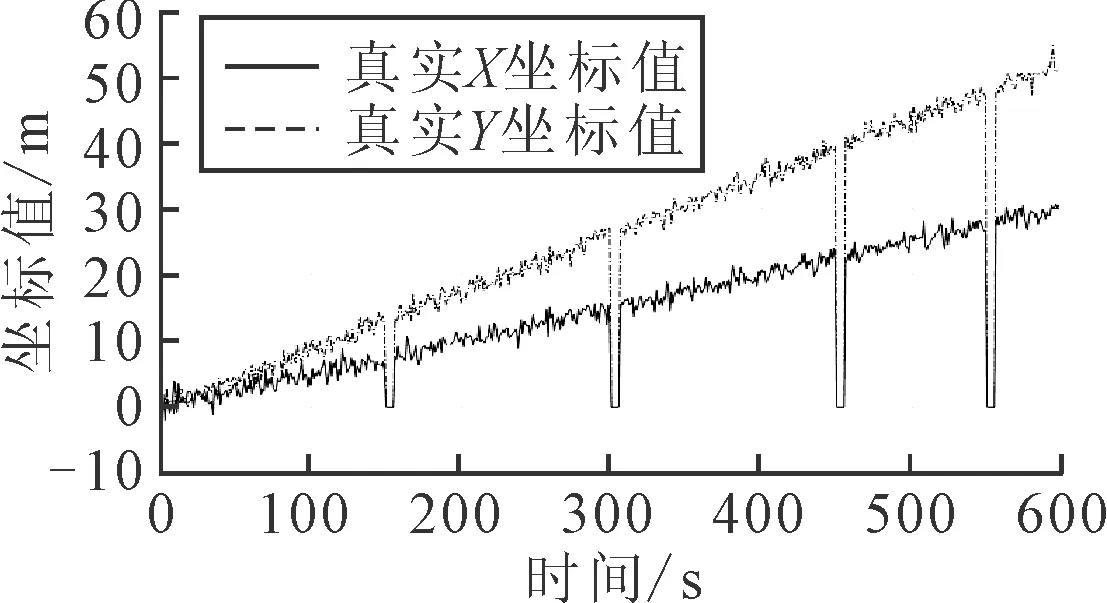
图3 带故障信息的传感器测量数据

由图3可知，最常见的传感器间歇性故障为传感器间歇性丢包.假定传感器在随机四个时刻传感器出现丢包现象，即获取到的数据为0.针对这种情形，分别采用三种滤波算法进行滤波处理，并将三种算法得到的结果与理想情况下的测量值进行对比，见图4.

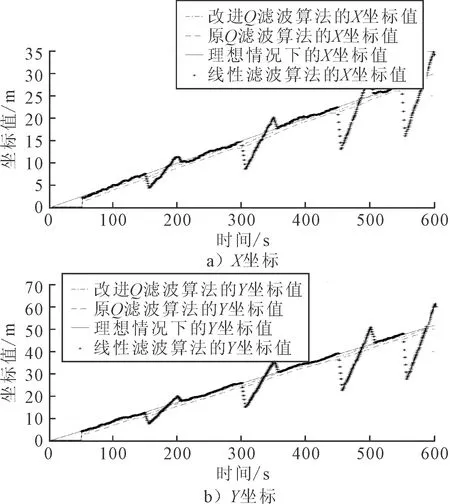
图4 3种算法滤波结果对比

由图4可知，线性滤波算法的容错性能较差；而原Q滤波算法虽然有较好的容错性能，然而存在数据延时的现象；改进Q滤波算法与理想情况下的测量值最为贴近.因此综合容错性能和滤波效果两个方面，改进Q滤波算法较其他两种算法更为理想.

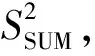
表1 传感器间歇性故障下三种滤波算法的评估指标对比

由表1可知，改进Q容错滤波算法在传感器发生间歇性故障情况下的3个评价指标相比于其他两种滤波算法均有较大幅度的减小，即在船舶直航工况下，改进Q容错滤波算法具有更良好的滤波性能及容错性能.

在算法耗时方面，采用原Q滤波算法和改进的Q滤波算法对长度为600的数据进行滤波处理，原Q滤波算法耗时约0.387 5 s，改进的Q滤波算法耗时仅约0.073 4 s.因此，改进的Q滤波算法与原Q滤波算法相比具有更好的快速性.

3.2 回转运动工况下的仿真对比

假定船舶以15°舵角做定常回转运动，图5a)为理想状态下船舶回转运动时大地坐标系下X，Y坐标值的变化曲线；图5b)为理想的船舶回转运动轨迹图.

图5 理想情况下的船舶回转运动位置测量值

由图5可知，当不存在噪声干扰及测量野值存在时，测量值可以近乎认为是真值.然而实际应用中，由于船舶在随机的环境中航行，加上船用设备对传感器的干扰，必然存在噪声项与测量野值，甚至会出现传感器间歇性故障(测量数据归零).图6为添加了均值为0，方差为2的高斯白噪声的测量数据，并假设在四个时间点传感器出现了间歇性故障.

由图6可知，添加了噪声项后，测量数据出现上下的波动，假定在随机四个时刻传感器出现丢包现象，数据为0.分别采用改进的Q容错滤波算法、原Q滤波算法和线性滤波算法，对真实数据进行滤波处理，并将滤波后的数据与理想情况下的测量值对比.图7a)为X坐标值的滤波结果；图7b)为Y坐标值的滤波结果.

图6 真实情况下的测量数据

图7 3种滤波算法结果对比

由图7可知，线性滤波算法在故障时刻附近数据发生跳变，故而容错性能较差；原Q滤波算法虽然有较好的容错性能，然而相比于理想情况下的测量值总有一段时间的滞后，因此实时性较差；改进的Q滤波算法与理想情况下的测量值最为吻合.因此相比于其他两种滤波算法，改进的Q滤波算法无论是在滤波效果还是容错性能方面均较为理想.

表2为采用平滑度指标对三种算法进行评估的结果，计算区间取t为100～500 s.

表2 传感器间歇性故障下三种滤波算法的评估指标对比

由表2可知，改进Q容错滤波算法在传感器发生间歇性故障情况下的各项评估指标相比于其他两种滤波算法均有较大幅度的减小，即在船舶回转运动工况下，改进Q容错滤波算法具有更良好的滤波性能及容错性能.

采用原Q滤波算法和改进的Q滤波算法对长度为600的数据进行滤波处理，原Q滤波算法耗时约0.362 1 s，改进的Q滤波算法耗时仅约0.051 9 s.因此，进一步验证了改进的Q滤波算法与原Q滤波算法相比具有更好的快速性.

4 模型试验验证

试验采用高精度定位传感器，可认为设定基站以设定坐标系.试验设定固定点坐标为(0，0)，截取试验过程中采集的某段控制周期内的位置信息分别绘制X，Y随控制周期的变化曲线，并分别采用原Q滤波算法和改进的Q滤波算法进行滤波处理.图8a)为X坐标随控制周期的变化曲线，图8b)为Y坐标随控制周期的变化曲线.

图8 X，Y方向坐标值随控制周期变化曲线

由于试验采用的定位模块自带滤除高频信号的功能，故而可以近似的认为噪声项非常小.由图8可知，定位传感器在第14个控制周期和第24个控制周期附近出现间歇性故障，由于试验系统采用数据存储然后使用的方式，故而传感器的间歇性故障表现为数据未刷新，即未采集到传感器的数据.从第10个控制周期开始采用两种算法进行滤波.由于原Q滤波算法的滤波值是窗口中间时刻的数据，即在第10个控制周期获得的数值为第5个控制周期的滤波值，因此在图9为出现跳变，且在第10个控制周期后，原Q滤波算法的数据存在延时滞后的现象，进一步验证了原Q滤波算法存在实时性的不足；相比而言，改进的Q滤波算法不仅具有良好的容错性能和滤波效果，而且滤波得到的数据的实时性更佳.

当传感器出现间歇性故障时，会导致无法获取智能船舶的位置等信息，虽然暂时性的丢包可能不会影响到最终绘制的轨迹，但是会直接影响到智能船舶的控制.例如本实验中出现丢包，系统读取不到当前时刻的信息，只能以上一时刻的数据作为控制器的输入，这样会导致控制器“致盲”，严重时可能会导致智能船舶发生碰撞等事故.由图9可知，当采用容错滤波算法后，尽管传感器无法获取船舶的位置参数，但是滤波器可以根据以往的数据及其变化趋势估计出该时刻的数值.

5 结 束 语

智能船舶自主控制的精度取决于传感器测量数据的准确度.然而诸多因素影响了传感器测量数据的准确度，从而降低了自主控制的精度.本文基于四分取样具有较强的容错性能这一优点，设计了一种改进的Q滤波容错算法.数值仿真和模型试验结果表明，针对智能船舶搭载的传感器出现间歇性的短时故障，本文改进的Q滤波算法可以估计出故障时刻可信度较高的数据，具有较强的容错性能和较好的滤波效果.

[1] CAMPBELL S, NAEEM W, IRWIN G W. A review on improving the autonomy of unmanned surface vehicles through intelligent collision avoidance manoeuvres[J]. Annual Reviews in Control,2012,36(2):267-283.

[2] 李家良.水面无人艇发展与应用[J].火力与指挥控制,2012,37(6):203-207.

[3] 贺辞.CCS《智能船舶规范》六大功能模块要求[J].中国船检,2016(3):84-85.

[4] EINICKE G A. Moothing,filtering and prediction:estimating the past,present and future[R].Rijeka Croatia：Intech Press,2012.

[5] YIN S, WANG G, YANG X. Robust PLS approach for KPI-related prediction and diagnosis against outliers and missing data[J]. International Journal of Systems Science,2014,45(7):1375-1382.

[6] 胡绍林,黄刘生.计算机控制系统容错设计技术及应用[M].北京：科学出版社,2010.

[7] 曾静,周永斌,张国良,等.基于有限记忆在线预测的卡尔曼滤波突变型故障容错设计[J].弹箭与制导学报,2004(4):272-275.

[8] 石静,缪玲娟.鲁棒容错滤波算法及在MEMS_SINS/GPS中的应用[J].北京理工大学学报,2012,32(2):146-149.

[9] 耿峰,祝小平,周洲.一种有效的组合导航容错滤波技术研究[J].西北工业大学学报,2016,34(3):449-455.

[10] GENG K K, CHULIN N A. Applications of multi-height sensors data fusion and fault-tolerant kalman filter in integrated navigation system of UAV[J]. Procedia Computer Science,2017,103:231-238.

[11] 雷江涛.容错组合导航系统中的联邦滤波器应用研究[J].舰船电子工程,2012,32(2):56-58.

[12] 张崇猛,王戈,舒东亮,等.自适应滤波的舰船综合导航系统信息融合技术[J].火力与指挥控制,2012, 37(7):39-42.

[13] 胡绍林,傅娜,郭文明.动态测量数据的高保真容错Q-滤波算法[J].宇航学报,2016,37(1):112-117.

[14] 马天宇,杭岑,杨松林.一种新型水面无人艇操纵性试验分析[J].江苏船舶,2016 (4):6-12.