船舶后尾轴承支承刚度对轴系回旋振动影响*

2018-05-02李小军朱汉华许浩然

武汉理工大学学报（交通科学与工程版） 2018年2期

李小军朱汉华秦源许浩然

(武汉理工大学能源与动力工程学院武汉 430063)

0 引言

船舶后尾轴承主要支撑尾轴和螺旋桨，承受着来自螺旋桨剧烈的动载荷作用.随着船舶的大型化，船体尾部刚度逐渐下降，尤其是后尾轴承总体支承刚度，而螺旋桨质量及其转动惯量却越来越大[1].负载过大或者轴系运转不稳定时，后尾轴承会出现润滑不良状况，引起油膜刚度波动，进而导致总支承刚度的变化[2]，因此进行尾轴承刚度各向异性下的轴系回旋振动研究是有必要的.

随着船舶大型化的发展，传递矩阵法和有限元法[3]被引入到回旋振动中.文献[1]对回旋振动的机理进行了研究，并从理论上讨论了支承刚度各向同性和各向异性的情况.文献[3]借助有限元软件，分析了螺旋桨陀螺效应、应力刚化效应和旋转软化效应等对轴系回旋振动的影响.

本文以某TEU集装箱船的推进轴系为研究对象，借助于有限元软件ANSYS，计入螺旋桨的陀螺效应，分析船舶推进轴系后尾轴承刚度各向同性和各向异性时回旋振动的异同，分别计算了其固有频率，画出其坎贝尔图并分析了其临界转速.

1 考虑陀螺效应的轴系振动方程

船舶轴系与径向滑动轴承之间通常采用油润滑，螺旋桨在非均匀伴流场中产生的不均匀推进力作用在轴系上，使轴颈偏离平衡位置，润滑油膜产生涡动，油膜刚度波动，导致总支承刚度波动，此时支承刚度呈现各向异性的状态[4].

1.1 螺旋桨陀螺矩阵

由于船舶螺旋桨的质量和惯量都比较大，其陀螺力矩会对轴系回旋振动产生较大影响.图1为支承刚度各向同性和各向异性时的陀螺力矩示意图.

图1 支承刚度螺旋桨的陀螺效应

其中当轴承刚度各向同性时，螺旋桨的陀螺力矩为

Mg=(Jpω-JdΩ)ωθ=JpΩ2θ(j0-1)

(1)

式中:Jp为极转动惯量;Jd为径向转动惯量;j0为转动惯量比，j0=Jp/Jd；h为频率比，h=ω/Ω.陀螺力矩包含2项：JpωΩθ为科氏惯性力矩；JdΩ2θ为牵连惯性力矩.

当油膜刚度变化引起支承刚度变化时，轴承刚度处于各向异性，此时陀螺力矩：

(2)

1.2 轴系动力方程

根据弹性力学，对于轴系这样的多自由度弹性系统，其通用动力学运动方程[5]为

(3)

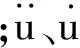
在有限元软件ANSYS的固定坐标系中，BEAM188梁单元通过将垂直于梁轴线的两个旋转自由度θy和θz与梁轴线自身的旋转自由度θx耦合，通过动量矩方程的推导，最终在梁单元矩阵中形成陀螺效应矩阵.计入螺旋桨陀螺效应后的转子的动力方程为

(4)

式中:Ggyr为陀螺效应矩阵，反对称阵，由于Ggyr中不含公转角速度Ω引起的牵连惯性力矩，而实际的集装箱船轴系公转角速度一般较大，其牵连惯性力矩不可忽略，因此ANSYS在计算支承刚度各向同性的回旋振动时，与实际可能会有一定偏差;B为旋转阻尼矩阵，因其值一般较小而忽略不计;令F=0，其齐次方程得到的特征值即为固有频率.

2 分析模型

2.1 轴系主要参数

本文研究对象是某大型集装箱船推进轴系，工作转速为104 r/min.轴系从主机至螺旋桨全长47.763 m，中间轴轴径为795 mm，尾轴外径975 mm，内径330 mm，含三个中间轴承和一个前尾轴承、一个后尾轴承，轴承刚度为1×109N/m.螺旋桨为6叶定距桨，根据Jasper给出的计算公式，螺旋桨附连水的质量、极转动惯量和径向转动惯量系数分别取1.1，1.25和1.5，得螺旋桨附水质量为120 353 kg，附水极转动惯量为454 250 kg·m2，附水径向转动惯量为272 550 kg·m2.

2.2 模型简化与建立

在建立有限元模型之前，需要对轴系进行一些简化[6].选用BEAM188单元对轴段进行模拟，对于轴段上的联轴器和推力轴承，可以通过设置梁的截面面积来模拟.通过适当延长尾轴长度来模拟螺旋桨的桨毂部分.螺旋桨及附连水的质量和转动惯量较大，采用MASS21质量单元，施加在螺旋桨的几何中心位置.联轴器的陀螺效应不计入.不考虑径向轴承交叉刚度和阻尼，采用COMBINE14弹簧单元进行模拟，在每个支撑位置的垂直和水平方向分别设置一个弹簧单元.弹簧的一端与轴系上轴承对应的节点相连，另一端设置为固定端.对弹簧单元的固定端施加全约束，约束推力轴承处节点的全部自由度，约束轴系在UZ和ROTZ上的自由度.

对模型进行网格划分，BEAM188单元66个，MASS21单元1个，COMBIN14单元10个.

3 计算结果分析与讨论

由于后尾轴承承受较大的负载，一般均有较大的油膜刚度，垂直方向上的油膜刚度要比水平方向上的油膜刚度大[7].采用QRDAMP特征值求解器，通过CORIOUS命令打开陀螺效应，并使用OMGEA命令施加自转角速度.所得的特征值为复数，其虚部为进动(回旋)频率，实部为衰减系数，且特征值成对出现，分别对应正回旋和逆回旋的固有频率[8].

3.1 固有频率计算

除了后尾轴承以外，其他各轴承刚度均保持为1×109N/m，后尾轴承分别取表1所示的三种刚度，进行模态分析，其一阶结果见表1.

由表1可知，当不计入螺旋桨的陀螺效应时，轴系的回旋振动便退化为横向振动.若后尾轴承水平和垂直刚度相同，出现一对方向共轭、大小相同的一阶固有频率；若后尾轴承水平和垂直方向刚度不同，出现一对方向共轭、大小不同的一阶固有频率.

表1 一阶正逆回旋固有频率表

注：Δ=(ω计入-ω不计)/ω不计.

当计入螺旋桨陀螺效应时，若后尾轴承水平和垂直刚度相同，螺旋桨的陀螺效应会使得逆回旋固有频率降低，正回旋固有频率提高；若后尾轴承水平和垂直方向刚度不同，陀螺效应对正逆回旋固有频率虽然也有影响，但明显不如各项同性时显著.分析式(1)～(2)，推断这可能是由以下两个因素造成：

1) 根据式(1)，支承各向同性时陀螺效应包含科氏力矩Jpω2θ和惯性力矩JdΩωθ.ANSYS中陀螺效应是建立在高速轴的基础上，即假定转子自转角速度远远大于公转角速度，其陀螺力矩主要是由转子自转角速度ω决定的.而本文中研究对象为大型低速集装箱船，其轴系转速较低，而公转角速度Ω有可能与自转角速度ω处于同一数量级，甚至更大，因此其牵连惯性力矩在陀螺效应中所作贡献不可以忽略.根据Mg=Jpω2θ-JdΩωθ，可以判断ANSYS在轴承各向同性时忽略了牵连惯性力矩，导致所计算的陀螺效应与实际有偏差.

保持其他轴承和后尾轴承垂直刚度均为1×109N/m，按照1×108～1×109N/m依次改变后尾轴承的水平刚度，转速保持104 r/min，进行模态分析，其结果见图2.

图2 一阶回旋(横向)振动固有频率

由图2可知，不计入陀螺效应时，随着水平刚度的降低，一阶逆回旋(水平方向横向振动)固有频率降低，而一阶正回旋(垂直方向横向振动)固有频率不变，即水平方向的刚度变化对垂直方向的横向振动固有频率无影响.

计入陀螺效应时，随着水平刚度的降低，其一阶正逆回旋固有频率曲线均逐渐逼近其一阶横向固有频率曲线，即陀螺效应逐渐减弱，且陀螺效应对正逆回旋固有频率的影响量相当，这说明水平方向的刚度变化同时影响了水平方向和垂直方向的陀螺矩阵，这在式(2)中找到解释：垂直方向的陀螺矩阵不仅仅包含轴自转角速度，还包括水平方向的旋转速度和旋转加速度.因此当水平方向刚度变化引起振动量变化时，垂直方向的陀螺矩阵也随之变化.

3.2 坎贝尔图计算

在船舶轴系回旋振动计算中，由于伴流场的激励特性，流体作用在轴系上的激振力是以螺旋桨的叶频为基频的.本文的研究对象为大型低速集装箱，其轴系转速较低，一般其固有频率(轴频临界转速)远远高于其工作转速，不大可能发生轴频共振.但是该船的螺旋桨有6个叶片，叶频和倍叶频的临界转速有可能落入到轴系工作转速范围内.改变轴系的自转角频率，分别画出各刚度下的坎贝尔图，见图3.

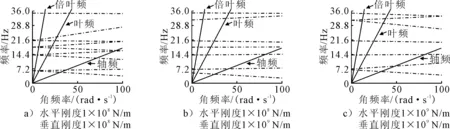
图3 各刚度下的坎贝尔图

由图3可知，陀螺矩阵主要为自转角速度的函数，因此当转速为零时，陀螺效应消失.若后尾轴承水平和垂直方向刚度相同，则其各阶正逆回旋曲线在零转速处重合.随着转速的提高，在陀螺效应的作用下，轴系各阶正回旋固有频率逐渐提高，逆回旋临界转速逐渐降低，临界转速从一个点变为一个区间并不断扩大；若轴承刚度水平和垂直方向刚度不同，则其各阶正逆回旋曲线在零转速处不重合，此时各阶临界转速在零转速处就已经不再是一个点，而是以两个方向上的横向振动固有频率为端点的区间，并且随着转速的增大，该区间进一步扩大.

该船在从启动加速到工作转速的期间，轴系转速虽然远远低于轴频临界转速，但是会经过叶频和倍叶频的临界转速区，且后尾轴承水平和垂直刚度不同时，其临界转速区域较大，这需要引起设计人员和驾驶人员的注意.