灰色系统理论在用水指标预测中的应用

李骁翔

(上海市供水管理处，上海 200081)

1 国内外研究现状

水是自然资源的重要组成部分，也是社会经济发展的重要物质基础。建立科学有效的水务统计方法是政府对水资源进行综合管理的重要手段，可以为政府宏观决策提供科学、准确的水资源基础信息，可以建立现代水务统计体系，进而促进并服务于绿色国民经济核算体系的建立[1-2]。

进行用水量指标预测分析是水务统计的重要工作内容。用水量指标预测的常用方法有分类用水量指标法和综合用水量指标法[3]。通常在用水量指标的预测分析中，首先要对现状各类用水量指标值进行测算，然后根据城市性质、发展目标和规模、经济社会发展愿景，考虑城市水资源的实际情况，综合确定各类用水量指标[4]。因此，用水量指标与城市经济水平、产业结构及各类用水特点等因素息息相关[5-7]。但目前，对需水管理的认识落后于实际需要，需水预测往往偏离实际，使水资源规划失去了对需水管理的指导作用，甚至带来负面影响。

1.1 用水量指标预测研究现状

用水量指标反映了用水效率和效益的高低。根据用水类别的不同，分别有反映工业用水、农业用水、生活用水及综合用水效率和效益的指标。对于工业用水，常用指标有万元GDP用水量、万元工业增加值用水量、工业用水重复利用率等；对于农业用水，常用指标有农田灌溉亩均用水量、农田灌溉水有效利用系数等；对于生活用水，常用指标有人均日综合生活用水量、人均日居民生活用水量等。

用水量指标是水务统计中极为复杂的一系列变量，具有周期性与随机性，与社会、经济、政治以及自然环境有着千丝万缕的联系。一方面，水务统计必须根据一定的社会与自然规律对用水量指标进行适度的调整；另一方面，用水量指标由于受到各种因素的影响，自然而然地会发生一些不规则的波动，从而对水务管理工作带来困难。因此，在对用水量指标进行预测前，应该充分考虑其变化特征及其影响因素，然后选择最为适合的预测方式，建立最为适合的预测模型。近年来，国内外学者在用水量指标、水量预测等方面的研究屡见不鲜，目前国内外应用较为广泛的预测方法主要有人均综合指标法、单位用地指标法、分类加和法、年递增率法以及灰色模型关联分析法等[8-10]。

国内外学者的研究表明，只有充分了解和掌握用水量指标变化的特点及规律，才能建立起符合实际情况的预测模型，从而提高预测精度。

1.2 灰色系统理论研究现状

灰色系统理论是基于信息的非完全性建立的一套全新的概念和方法，其研究目的在于根据已知的信息建立数学模型，从而预测系统的未知信息。该理论认为系统内部特性确知的为白色系统，内部特性未知的为黑色系统，内部特性部分确知、部分未知的为灰色系统。经过30多年的发展，灰色系统理论已基本建立起一门新兴学科的结构体系，其主要内容包括以灰色代数系统、灰色方程、灰色矩阵等为基础的理论体系，以灰色序列生成为基础的方法体系，以灰色关联空间为依托的分析体系，以灰色模型(GM)为核心的模型体系，以系统分析、评估、建模、预测、决策、控制、优化为主体的技术体系。该理论已经广泛应用于农业、经济、医疗、生态、水利、气象、地质、军事、文化、交通、管理、工业控制等几十个领域[11]。

灰色系统理论以“部分信息已知、部分信息未知”的“小样本”、“贫信息”不确定型系统为研究对象。

(1)用灰色数学来处理不确定量，使之量化

在数学发展史上，最早研究的是确定型的微分方程，即在拉普拉斯决定论框架内的数学。他认为一旦有了描写事物的微分方程及初值，就能确切知道事物任何时候的运动。随后发展了概率论与数理统计，用随机变量和随机过程来研究事物的状态和运动。模糊数学则研究没有清晰界限的事物，如儿童和少年之间没有确定的年龄界限加以截然划分等，它通过隶属函数来使模糊概念量化，因此能用模糊数学来描述，如语言、不精确推理以及若干人文科学。灰色系统理论则认为不确定量是灰数，用灰色数学来处理不确定量，同样能使不确定量予以量化。

(2)充分利用已知信息，寻求系统的运动规律

研究灰色系统的关键是如何使灰色系统白化、模型化、优化。灰色系统视不确定量为灰色量。提出了灰色系统建模的具体数学方法，它能利用时间序列来确定微分方程的参数。灰色预测不是把观测到的数据序列视为一个随机过程，而是看作随时间变化的灰色量或灰色过程，通过累加生成和累减生成逐步使灰色量白化，从而建立相应于微分方程解的模型，并做出预报。这样，对某些大系统和长期预测问题，就可以发挥作用。

(3)灰色系统理论能处理贫信息系统

灰色预测模型只要求较短的观测资料，这和时间序列分析、多元分析等概率统计模型要求较长资料很不一样。因此，对于某些只有少量观测数据的项目来说，灰色预测是一种有用的工具。

从国内外研究进展看，在用水量指标预测分析中开展灰色关联理论研究在技术上具有一定的科学性和可行性[12]。

1.3 研究内容

本文通过运用灰色系统理论中的灰色预测模型，对某市的各项用水量指标进行预测分析，以便摸清用水量指标的变化趋势，从而形成简洁便捷，且长期有效的计算方法，对管理决策中涉及的用水量指标进行科学的预测分析，意图通过新方法的应用，强化和完善原有的统计方法，为今后的水务统计管理提供新的工作思路和理论支撑。

2 GM(1,1)模型

灰色预测模型称为GM模型，目前适用最广泛的灰色预测模型就是关于数列预测的一个变量、一阶微分的GM(1,1)模型。GM(1,1)是基于随机的原始时间序列，按时间累加形成的新的时间序列呈现的规律可用一阶线性微分方程的解来逼近。经证明，一阶线性微分方程的解逼近所揭示的原始时间数列呈指数变化。因此，当原始时间序列隐含着指数变化规律时，建立一个一阶变量的灰色系统模型[GM(1,1)模型]，包括灰色序列生成、指数规律检验、模型参数估计、模型误差检验4个步骤，灰色模型GM(1,1)的预测将是非常成功的。灰色模型实质是对原始数据序列做一次累加生产，使生成序列呈一定规律，并用典型曲线拟合，从而建立其数学模型，其构造如下：

对已知原始数据序列X(0)={x(0)(k)}(k=1,2,…,n)，进行一阶累加生成新数列X(1)。

(1)

利用X(0)构成白化微分方程，如式(2)。

(2)

其中：a、u—待定系数。

采用最小二乘法确定，如式(3)。

(3)

式(3)中，数据矩阵B与yN如式(4)和式(5)。

(4)

(5)

得出预测模型，式(6)。

(6)

使用平均相对误差对模型进行精度检验，如式(7)。

(7)

若精度达不到预期要求，可通过残差模型进行修正或对原始数据序列进行适当取舍，以提高模型精度。最后对模型算出序列进行逆运算还原，得到预测结果[13]。

3 用水量指标预测

3.1 形成预测模型

根据灰色系统理论，各用水量指标的预测是以以往用水量指标为原始序列，以时间为状态变量，对系统行为数列的变化预测，所以可建立GM(1,1)预测模型。本节选取某市水资源公报中的用水量指标组成预测模型的原始数列。

以2004年～2013年人均年用水量，预测2014年～2016年近3年的人均年用水量变化情况。

(1)选取2004年～2013年人均年用水量为原始数列，进行一阶累加生成新数列，如式(8)。

X(0)={646,617,590,568,546,512,437,

415,366,369}X(1)={646,1 263,1 853,2 421,2 967,3 479,

3 916,4 331,4 697,5 066}

(8)

(9)

(10)

最终得式(11)。

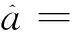
(11)

(3) 确定预测模型

根据已计算出的待定系数a、u，得出人均年用水量预测模型，如式(12)。

(12)

(4) 对预测模型进行精度检验

按照预测模型，各人均年用水量实际值与模拟值、两值间的绝对误差及相对误差如表2所示。

表1 2004年～2013年某市主要用水量指标Tab.1 Main Water Consumption Indexes during 2004 to 2013

表2 精度检验计算表Tab.2 Accuracy Test Calculations

图1 人均年用水量实际值与模拟值折线图Fig.1 Line Chart of Actual and Analog Values for Annual Water Consumption per Capita

2004年～2013年人均年用水量的实际值与模拟值具有较好的拟合，也证明了该预测模型具有较好的预测精度，预测结果具有较高的可信度。

(5) 进行逆运算，确定预测结果

因此，运用GM(1,I)模型对人均年用水量进行预测，其结果如表3所示。

通过同样的计算和检验过程，得出各用水量指标预测模型。

人均年用水量预测模型如式(13)。

(13)

万元GDP用水量预测模型如式(14)。

(14)

万元工业增加值用水量预测模型如式(15)。

(15)

人均日综合生活用水量预测模型如式(16)。

(16)

人均日居民生活用水量预测模型如式(17)。

(17)

表3 人均年用水量预测结果Tab.3 Forecast Results of Annual Water Consumption per Capita

3.2 计算预测结果

根据各用水量指标预测模型，2014年～2016年某市主要用水量指标预测结果如表4所示。

3.3 预测结果精度检验

作为验证，将2014年主要用水量指标的实际值与GM(1,1)模型预测结果，以及传统预测方法的结果分别进行比对。传统的年递增率法主要是使用指标的当年值与上年值的增减变动比率来预估下一年的指标数值，即式(18)。

(18)

对比结果如表5所示。由表5可知，通过模型计算出的用水量指标预测值与实际值间的相对误差均小于0.05，且优于传统预测方法计算出的预测值与实际值间的相对误差，拟合度更高。总体来说，各用水量指标的预测模型在实际应用方面效果较传统预测方法更好。

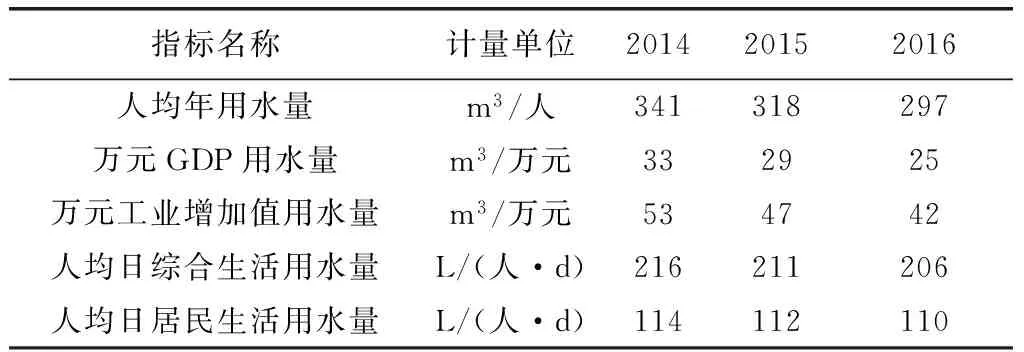
表4 某市主要用水量指标预测结果Tab.4 Forecast Results of Main Water Consumption Indexes

表5 2014年主要用水量指标实际值与预测值对照表Tab.5 Comparison of Actual and Predicted Values for Main Water Consumption Indexes in 2014

4 结论

(1)本文所得预测模型和预测结果可为用水量指标预测和水务管理提供依据；灰色系统理论在用水量指标预测分析中的成功应用，也为今后水务统计管理提供了新的思路和理论支撑。

(2)灰色系统理论中的GM(1,1)模型经论证，在不掌握大数据的情况下，能够快速、有效地形成科学的预测模型，且预测结果与实际值的拟合程度较高，具有较好的预测效果，能够客观反映各用水量指标的变化趋势，强化和完善了原有的统计预测方法。

(3)本文中得出的用水量指标预测模型及预测结果虽给出了指标的相对评价，但并没有测定各用水量指标的绝对水平，这也是本方法的不足与待改进之处，其更合理数值有待进一步研究，需在实践过程中逐步改进和完善。

[1]沈大军,姜素梅.城乡水务一体化管理的制度分析[J].水利学报,2005,36(9):1143-1146.

[2]魏贵良,孔凡亮,周长勇,等.水务一体化管理存在问题与对策研究[J].水利天地,2006,23(7):12-14.

[3]丁惠英,丁民.国外城市水务管理经验分析[J].中国水利,2003,54(4):47-49.

[4]赵茜.适应水务体制改革要求探索水利统计方法创新[J].中国水利,2007,58(18):23-24.

[5]高立洪.进一步推进和深化水务管理体制改革[N].中国水利报,2004-11-30.

[6]仇保兴.以科学的发展观指导城市水务工作[J].住宅产业,2006,3(10):4-5.

[7]黄高亮,李甘雨.基于节水理念的温州人均综合用水量指标研究[J].规划师,2014,30(s3):291-294.

[8]林英姿,刘万全,李冠.利用灰色模型预测年用水量[J].中国资源综合利用,2014,33(11):57-59.

[9]张雅君,刘全胜.需水量预测方法的评析与择优[J].中国给水排水,2001,17(7):27-29.

[10]王志伟,闫来洪,赵朝成,等.开发区工业用水量预测方法研究[J].四川环境,2009,28(3)：37-40.

[11]党耀国,王正新,刘思峰,等.灰色预测与决策模型研究[M].北京:科学出版社,2009:86-97.

[12]肖新平,毛树华.灰预测与决策方法[M].北京:科学出版社,2013:18-26.

[13]王正新,党耀国,刘思峰.基于离散指数函数优化的GM(1，1)模型[J].系统工程理论与实践,2008,28(2):62-67.