Fractional-order Sparse Representation for Image Denoising

Leilei Geng,Zexuan Ji,Yunhao Yuan,and Yilong Yin

I.INTRODUCTION

IMAGE denoising is one of the most important research subjects in image processing due to its fundamental role in a number of applications,such as medical imaging,remote sensing,surveillance and entertainment.Generally,the observed noisy imageycan be formulated asy=x+n,wherexis the clean image andnis an additive white Gaussian noise with zero-mean and standard deviationσ.In the past decades,extensive studies have been conducted to develop various image denoising approaches,such as total variation(TV)regularization[1],non-local means(NLM)algorithm[2]and block-matching and 3D(BM3D) filtering algorithm[3].Although classical approaches are effective in removing noise artifacts,the TV regularization tend to over-smooth images due to the piecewise constant assumption and the computational complexity of the BM3D is extremely high.As an alternative,sparse representation-based models have recently led to promising results[4]-[7].

Sparse representation-based models assume that an imagexcan be represented asx≈Dα,whereD∈Rn×mis an over-complete dictionary and most entries of the sparse coefficientsαare zero or close to zero.The sparse decomposition ofxcan be obtained by solving anl0-minimization problem,i.e.,α= argminα‖α‖0,s.t.‖x-Dα‖2≤ε,where‖·‖0is a pseudo norm andεis a small constant.Sincel0-minimization is a NP(none-deterministic polynomial)-hard combinatorial optimization problem,it is often relaxed tol1-minimization.Thel1-norm based model can be solved efficiently by convex optimization techniques,formulated as{α,D}=argminα{‖x-Dα+λ‖α‖1},whereλdenotes the regularization parameter.Many efficientl1-minimization techniques have been proposed,such as iterative thresholding algorithms[8],[9],Bregman split algorithms[10],[11]and so on.

Dictionary learning is a key problem of sparse representation-based models.Comparing with analytically designed dictionaries(e.g.,the wavelet/curvelet dictionary),dictionaries learned from example image can greatly improve the denoising performance because they can better characterize the image structures[12]-[16].For example,[16]estimated the sparse coefficients by exploiting nonlocal self-similarity in the observed image.Recently,most conventional sparse representation-based models concentrate on learning the adaptive dictionary directly from the noisy image itself instead of from the external image database.The main advantages are that the self-structural information is exploited and the trained dictionary is adaptive to the image of interest.However,the training samples extracted directly from the observed image are inevitably corrupted by noise.Thus,accurate sparse coefficients and optimal dictionary cannot be obtained efficiently in the noisy sample space.Consequently,the performance and efficiency of conventional sparse representation-based models are limited.

In this paper,we propose a fractional-order sparse representation(FSR)model to obtain better estimations for both the sparse coefficients and the dictionary.First,we cluster external training image patches into multiple groups to explore image self-similarity.Then we calculate the singular values for each clean/noisy patch pair in the wavelet domain and learn the uniform fractional-order parameters for each cluster.To deal with the noisy image,a novel sample space is constructed using adaptive fractional-order parameters in the wavelet domain.In this way,we can obtain more accurate sparse coefficients and dictionary for image denoising.Comparing with several state-of-the-art sparse representation-based models[4],[16]and the BM3D algorithm[3],our proposed FSR model clearly performs better in terms of both denoising performance and computational efficiency.

II.BACKGROUND AND RELATED WORK

A.Sparse Representation-based Denoising Model

Given the dictionaryDx,an image patchxi=Rix,extracted from the clean imagexat the locationi,can be sparsely represented by solving the non-convexl1-optimization:

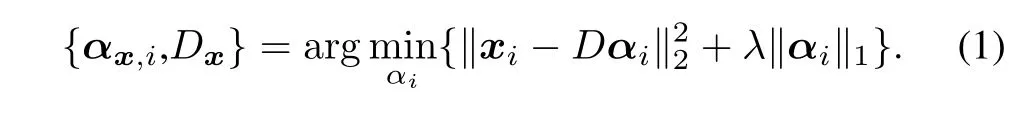
Then,the target imagexcan be constructed by averaging each image patchxiwith a straightforward least-square solution in[12]:

The conventional sparse representation(SR)denoising models recoverxfrom noisy imageyby solving the following minimization problem:

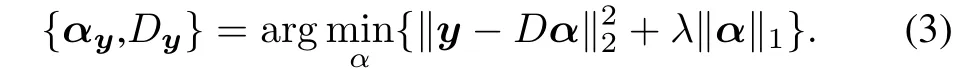
Then,by adding auxiliary variablexi=Dyαy,i,the denoised imagexb is reconstructed with a closed-form solution in[17]:

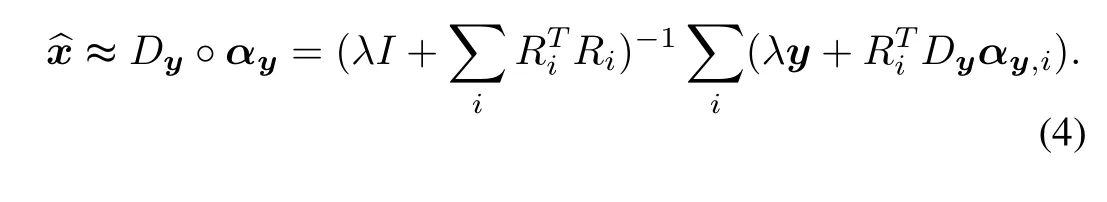
B.Fractional-order Technique

In recent years,the fractional-order technique has been widely used in image denoising[18],texture enhancement[19],image reconstruction[20],face representation[21],and other applications.Reference[18]proposed a fractional-varying-order differential-based method for image denoising.This method varied the gradient of images to suppress the blocky effect.Moreover,it retained more texture details than the integral order partial differential denoising model due to the fractional differential amplitude frequency.Reference[19]presented a fractional differential-based method for multi-scale texture enhancement.This method could nonlinearly enhance complex texture details,which has been proven superior to traditional integral-based algorithms.Reference[20]incorporated fractional derivatives and edge detection in a method called fractional-order partial differential-based image reconstruction.The fractional derivative has been demonstrated to be superior to the integer derivative.In face representation,[21]proposed a fractional-order embedding canonical correlation analysis to reduce the dimensionality of multi-view data.This method constructed the fractional-order both within-set and between-set scatter matrices to alleviate the deviation of the eigenvalues and singular values in the corresponding sample covariance matrices.We can conclude that the fractional-order technique targets at a more general framework of nonlinear and flexible data processing mode.Therefore,we introduce the fractional-order technique into the sparse representation model to obtain more accurate sparse coefficients and dictionary.

III.MODELING OF FRACTIONAL-ORDER SPARSE REPRESENTATION

A.Motivation

For effective image denoising,the dictionaryDyand the sparse coefficientsαyobtained by solving the minimization problem in(3)are respectively expected to be as close as possible to theDxand theαxobtained by(1).However,due to the noise in the observed image,Dyandαywill deviate from their true values.Thus,bothDyandαycannot be considered as good approximations,and would directly decrease the quality of the denoised image.To further illustrate these difference,we de fine the deviation degree of the dictionaryDyas Dev(Dx,Dy)and the deviation degree of the sparse coefficientsαyas Dev(αx,αy).

Definition 1:SupposeDx={dx,1,dx,2,...,dx,m}is an over-complete dictionary containingmdictionary atoms learned from the original imagex,andDy={dy,1,dy,2,...,dy,m}is an over-complete dictionary containingmdictionary atoms learned from the noisy imagey.Then,the deviation degree of the dictionaryDyis de fined as:

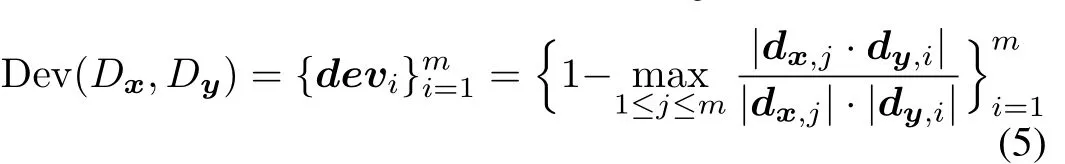
where Dev(Dx,Dy)denotes the deviation degree vector of the dictionaryDy,devidenotes theith deviated element referring to theith dictionary atomdy,i,anddx,j·dy,idenotes the inner product ofdx,janddy,i.The definition of Dev(Dx,Dy)describes the ability that the dictionaryDyexpress the noisy imagey.When the Dev(Dx,Dy)is zero,theDyis as the same as theDxand the noise can be restrained effectively.

Definition 2:Suppose thatαxis the sparse coefficients of the clean image patch andαyis the sparse coefficients of the noise image patch.Then,the deviation degree of the sparse coefficientsαyis defined as:

where‖·‖Fdenotes the Frobenius norm.The definition of Dev(αx,αy)describes the similarity betweenαxandαy.As the Dev(αx,αy)is close to zero,the sparse coefficientsαyis similar to its corresponding true valueαx.

To show the deviation degrees,we conducted experiments using the Lena image.We added Gaussian white noise(σ=20)to the original imagexto obtain the noisy imagey.For fair comparison,bothαxandαywere obtained using fixed discrete cosine transform(DCT)bases.Figs.1(a)and 1(b)plot the distributions of Dev(Dx,Dy)and Dev(αx,αy),respectively.

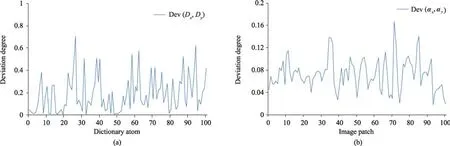
Fig.1.Distributions of Dev(Dx,Dy)and Dev(αx,αy)when the Lena image is noisy(σ =20).

Fig.2.Flowchart of the proposed FSR model.

Note that most deviation degrees of dictionary atoms are over 0.1 and the highest value is about 0.71.As shown in Fig.1(b),more than 80%of Dev(αx,αy)concentrated in 0.05-0.12.Hence the accurateαyand optimalDycannot be obtained from the noisy image by the SR models.The definitions of Dev(Dx,Dy)and Dev(αx,αy)indicate that it is possible to further improve the denoising performance by improving the accuracy of bothαyandDy.However,it is difficult to directly improve the accuracy ofαyandDyin the observed sample space due to noise disturbance.To address this problem,we construct a novel sample space by correcting singular values utilizing the cluster-based fractional-order technique with adaptive parameters in the wavelet domain.

B.Fractional-order Sparse Representation Model

The FSR model involves the training phase and the denoising phase:

In the training phase,we learn the fractional-order parameters from external image database including four steps:

Step 1:We cluster the training image patches intoKclusters(typicallyK=10)usingK-means algorithm and decompose those patches into frequency sub-patches by the discrete Haar wavelet transform;

Step 2:We calculate singular values for each patch;

Step 3:The fractional-order parameterηijof each patch is obtained given the clean/noisy patch pairs;

Step 4:We compute the uniform fractional-order parameterηifor each training patch group with similar textures.

In the denoising phase,the noisy image is first decomposed into Haar wavelet images.Then the fractional-order parameter is employed to construct the novel fractional-order sample space,and the denoised image is reconstructed by sparse coefficients and dictionary.The flowchart of the FSR model is shown in Fig.2.

1)Deviation Degree of Singular Values:For an image patchxi,we have the singular value decomposition(SVD)[22]asxi=PiΛiQi,wherePiandQiare the left and right singular matrices,respectively,Λi=is a singular value matrix,andare the descending order singular values.The singular values can be interpreted as the variance estimation and they expose the geometric structure of the image.Hence,the singular values represent the intrinsic and algebraic properties containing illumination,noise and texture.Due to the disturbance of noise,the singular values obtained from the noisy image deviate from their true values.Similarly,we can de fine the deviation degree of singular values as Dev(Λx,Λy).

Definition 3:SupposeΛx=denotes the singular value matrix of the original image patch,andΛy=denotes the singular value matrix of the noise image patch.Then,the deviation degree of the singular values is de fined as:

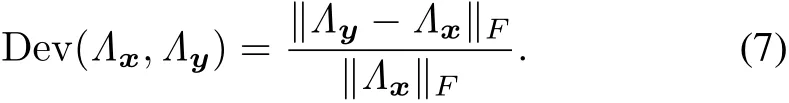
Fig.3. Deviation degree of singular values.

To show the deviation degree of the singular values,we plotted the distribution of Dev(Λx,Λy)in Fig.3,whereΛywas computed from the noisy Lena image(σ=20).As observed in Fig.3,it is evident that the singular values differ greatly from their true values and most Dev(Λx,Λy)are over 4.Recently,this deviation has been demonstrated to have a negative effect on classification systems[21].Motivated by the above situation,we re-estimate the singular values using fractional-order techniques.

2)Multi-scale Decomposition:As mentioned above,due to disturbance of noise,the singular values deviate from their true values.The denoised image would involve unexpected perturbations when the singular values are directly obtained from the noisy image space.As illustrated in Fig.4,the re-estimated image Fig.4(c)is directly reconstructed using the corresponding singular values obtained from the original Lena image Fig.4(a).Although the extrinsic disturbance(noise)is restrained(e.g.,Fig.4(b)),other new disturbances are involved.Because the extrinsic factor(noise)can be largely isolated from the intrinsic factor(texture)in the frequency sub-spaces,the re-estimated sample space can avoid these unexpected perturbations.Thus,it is necessary to correct the singular values of noisy image patches in the wavelet domain.

Fig.4.Comparison of experimental results.

Fig.5. Comparison of PSNRs with various cluster numbers and various noise levels.

3)Fractional-order Parameter Learning:Since the proposed FSR model involves the fractional-order technique,the key problem is that how to choose the fractional-order parameterη.In this paper,we first cluster the training image patches intoKgroups using theK-means clustering method.For each patch in theith cluster,we calculate the fractional-order byηij=argmin Dev(Λx,Λy).Then the uniform fractional-order parameterηifor each training group is obtained byηi=argminηiP‖ηi-ηij‖2F.Furthermore,the cluster numberK(typicallyK=10)is determined by a series of experiments.We utilize the cross-validation method to determine the parameterKwith optimal peak signal to noise ratio(PSNR)of the denoised image.Fig.5 plots the distribution of PSNR average results over five typical images(e.g.,Lena/Barbara/Boat/House/Pepper).We can see that there is little improvement of the image denoising performance over all noise levels as the cluster number increases.Therefore,we cluster the samples into 10 groups in terms of the effectiveness and efficiency.

4)Fractional-order Image Denoising:With the trained fractional-order parameters,we denoise the image in the novel fractional-order sample space.Now,we define the fractional-order patch as follows:

Definition 4:Supposeis a fractional-order parameter,and each fractional elementsatisfies 0≤ηk≤1.Then,the fractional-order patch is referred to as:

wherePiandQiare respectively the left and right singular matrices of the noisy patchyi,anddenotes the fractional-order singular value matrix.In Definition 4,it is obvious that the decomposition in(8)subsume the thin SVD as a special case whenη={1,1,...,1}.Based on Definition 4,the following properties are observed:

Property 1:The rank ofis equal to the rank ofyi,i.e.,rank()=rank(yi).

Property 2:where‖·‖Fdenotes the Frobenius norm.

Property 1 shows the basic characteristics of the novel fractional-order sample.Property 2 reveals that the space distance between andyican be controlled by adjusting the fractional-order parameterη.

After constructing fractional-order patches,we build a novel sparse representation-based model for image denoising.The proposed fractional-order image denoising phase is an iterative algorithm that alternates between fractional-order sample space construction and dictionary learning.In the fractional-order sample space construction stage,the noisy image is first decomposed into different frequency sub-spaces by the discrete Haar wavelet transform with 2 levels.For a noisy patch,we calculate the distance between it and all clustering centers of groups.Then we construct the fractional-order patch using the corresponding fractional-order parameter of the nearest patch group.In the sparse coding and dictionary learning stage,we calculate sparse coefficients for fractional-order patches and update dictionary atoms.Finally,the denoised image can be reconstructed by overlapping image patches.Therefore,the proposed algorithm can be summarized in Algorithm 1.

IV.EXPERIMENTAL RESULTS AND ANALYSIS

To demonstrate the superior performance of the proposed FSR model,in this section,we presented extensive experiment results on five typical images with simple and complex textures with various noise levels.We compared the proposed FSR model with three current state-of-the-art image denoising approaches:the conventional sparse representation(SR)denoising model[4],nonlocally centralized sparse representation(NCSR)denoising model[16]and the BM3D image denoising with shaped-adaptive principal component analysis(SAPCABM3D)algorithm[3](it is an enhanced version of BM3D denoising in which local spatial adaptation is achieved by shaped-adaptive principal component analysis(PCA)).

Algorithm 1 Fractional-order Image Denoising Algorithm

In the proposed FSR model,40000 overlapping image patches of size 8×8 were directly extracted from noisy images and were clustered into 10 groups.The fraction-order patches in each cluster were constructed using their corresponding fraction-order parameters in the discrete Haar wavelet domain.Then we trained a redundant dictionary of size 64×256 based on the initial DCT dictionary.Finally,the denoised patches were averaged using the Lagrange multiplierλ=30/σ,as described in(4).The SR denoising model trained a dictionary based on the 40000 image patches of size 8×8 extracted from the noisy images using the same parameters as those of the proposed FSR model.The NCSR denoising model clustered patches into 70 groups and computed the sparse coefficients using iterative shrinkage algorithm(parameters details in[16]).The SAPCA-BM3D algorithm was applied to the noisy image using a shape-adaptive transform basis.In this method,similar blocks were found in a 25×25 local neighborhood using block matching with the maximumd-distanceτ=2500.In the collaborative filtering stage,PCA was employed as part of the 3D transform.

A.Comparison of Denoising Performance

To demonstrate the denoising performance of the proposed FSR model,we performed a set of experiments on five typical images:Lena,Barbara,Boat,House and Pepper.The experiments were performed 10 times,and the average results were reported for five noise levelsσ=5,10,20,35,50.We evaluated the quality of the denoised images using the popular PSNR(in dB)and structural similarity index measurement(SSIM).

The PSNR results are listed in Table I.As seen in Table I,the proposed FSR model obtains excellent denoising performance,and 72%PSNR results are the best among four comparison approaches.Although the SAPCA-BM3D algorithm obtains 20%of the best PSNR results,the approach is very time-consuming as described in Section IV-B.Note that,with little disturb of the noise,most textures are preserved at the lowest noise levelσ=5.For the smooth Pepper image,the SAPCA-BM3D algorithm can sufficiently exploit the self-similarities of patches.Hence,the SAPCA-BM3D result(38.30dB)is superior to sparse representation-based results,i.e.,the SR result(37.79dB),the NCSR result(38.06dB)and the proposed FSR result(37.78dB).

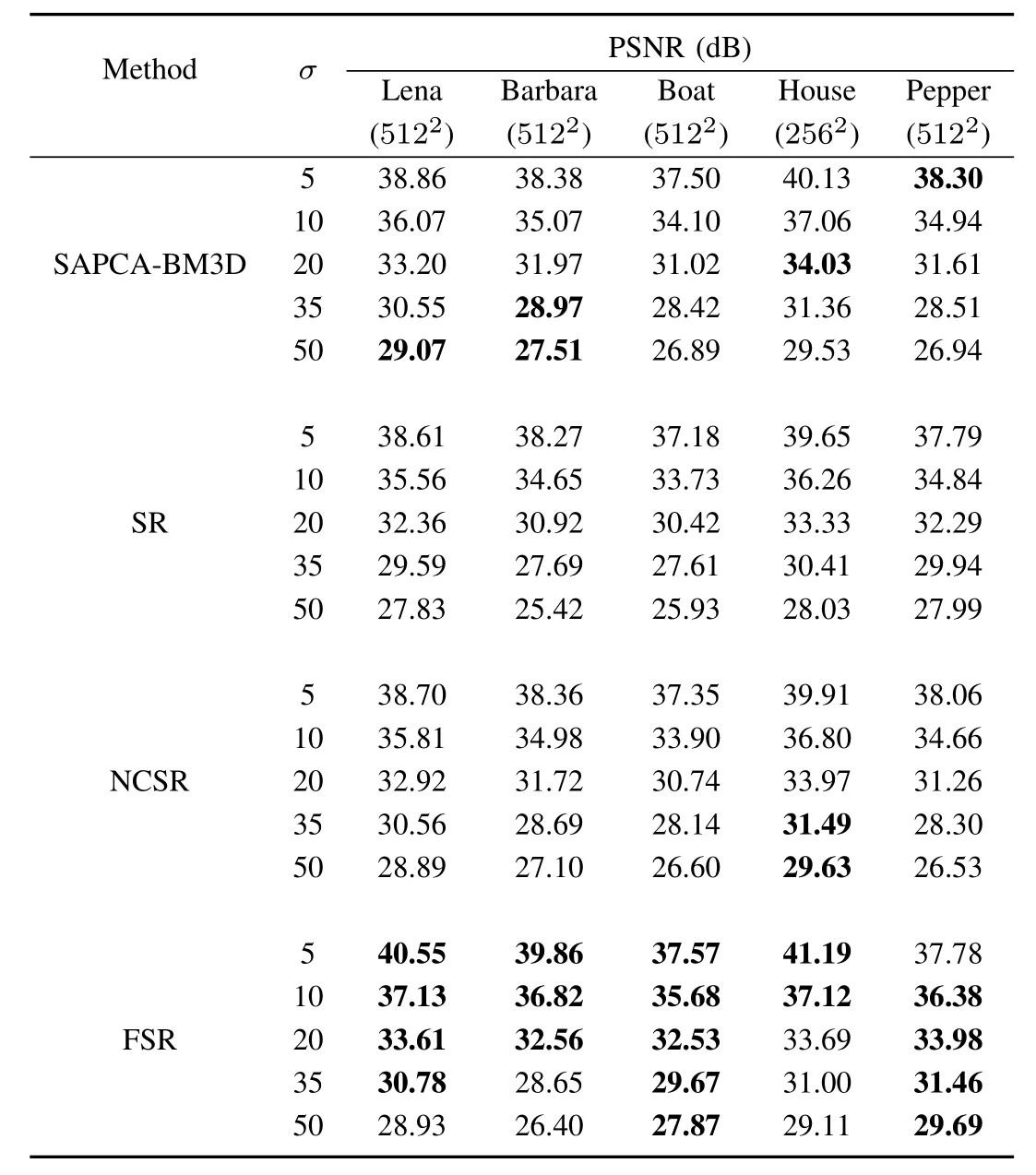
TABLE IAVERAGE DENOISING RESULTS(PSNRIN DB)FOR VARIOUS NOISY LEVELS,OBTAINED BY THE SAPCA-BM3D,SR,NCSR AND FSR MODEL.THE BEST RESULT IS HIGHLIGHTED.

To better visualize the experimental comparison,Fig.6(a)presents the average PSNR results over all test images for each noise level.Note that the FSR model leads to the best denoising performance on all noise levels.Although the FSR does not exploit image self-similarities as the SAPCA-BM3D algorithm does,the FSR outperforms SAPCA-BM3D by 0.96dB.The FSR model outperforms other two sparse representation-based models:the SR model by up to 1.35dB and the NCSR model by up to 1.0dB,respectively.Furthermore,the NCSR model performs almost the same as the SAPCA-BM3D algorithm.In terms of the PSNR standard deviation,as depicted in Fig.6(b),the FSR model improves the robustness for four out of five noise levels.Due to the weak capacity of the FSR model for the smooth Pepper image,the FSR model falls behind other three models at the low noise levelσ=5.

For further evaluation of the denoising performance,we calculated the SSIM results of the denoised images.Table II shows that 56%of the SSIM results obtained by our proposed FSR model are higher than those obtained by other three approaches.Note that,for the smooth Pepper image,the average SSIM result is 0.87 for the SAPCA-BM3D algorithm,0.84 for the SR model,0.88 for the NCSR model and 0.85 for the FSR model.Thus,for a smooth image,the NCSR model achieves a better result than other two sparse representation models(e.g.,SR/FSR).However,the proposed FSR model outperforms best in most cases.

TABLE IIAVERAGE DENOISING RESULTS(SSIM)FOR VARIOUS NOISY LEVELS,OBTAINED BY THE SAPCA-BM3D,SR,NCSR AND FSR MODEL.THE BEST RESULT IS HIGHLIGHTED.

Figs.7(a)and 7(b)show the visual comparison of the average SSIM and their standard deviation.Fig.7(a)shows that the FSR is slightly better than other three methods for low and moderate noise levels(σ=5,10,20).Because the SAPCA-BM3D algorithm and NCSR model utilize the structural similarity among numerous similar image patches,the corresponding results are superior to the FSR results at the high noise levels(σ=35,50).In terms of the SSIM standard deviation,as depicted in Fig.7(b),the proposed FSR model improves the robustness except at the low noise level(σ=5).

Figs.8–10 illustrate the visual comparison of denoised results for three typical images(Pepper,Boat and Barbara)at moderate noise levels(σ=20).Figs.8(a)-8(e)show the denoised images,and Figs.8(g)-8(j)show the corresponding noisy components.It can be observed from Fig.8 that the FSR model delivers the best visual quality.The SAPCA-BM3D and SR methods tend to suffer from noticeable artifacts around the smooth areas,as shown in Fig.9.Furthermore,for regions with complex textures,the superiority of the FSR model is visually justified by Fig.10.

Thus,the FSR model can both preserve the sharpness of edges and suppress undesirable artifacts.Based on the above discussion in this sub-section,we can conclude that the FSR model improves the denoising performance and robustness in terms of the PSNR and SSIM.

Fig.6.Comparison of the average and the standard deviations of PSNR on various noise standard deviations.

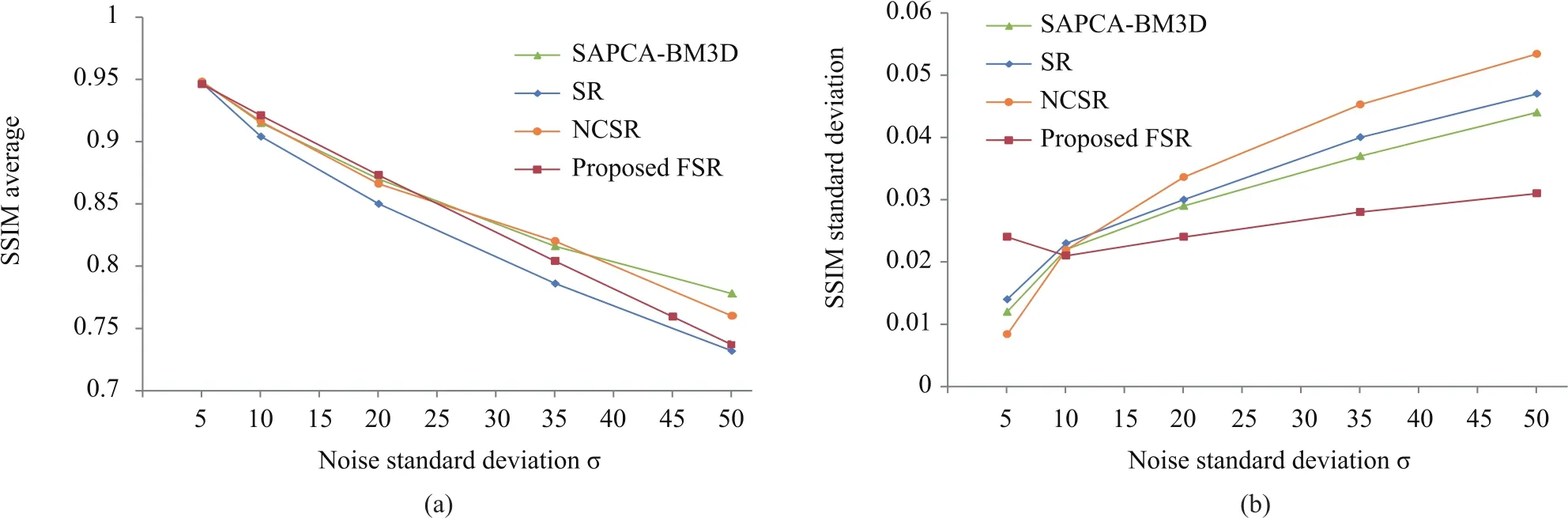
Fig.7. Comparison of the average and the standard deviations of SSIM for various noise standard deviations.

Fig.8.Denoising performance comparison on the Pepper image with moderate noise corruption.(a)Noisy image(σ=20);denoised images by(b)SAPCABM3D(PSNR=31.61dB,SSIM=0.88);(c)SR(PSNR=32.29dB,SSIM=0.84);(d)NCSR(PSNR=31.26dB,SSIM=0.88);(e)FSR(PSNR=33.98dB,SSIM=0.86);(f)real noisy component;corresponding noisy components by(g)SAPCA-BM3D;(h)SR;(i)NCSR;(j)FSR.

Fig.9.Denoising performance comparison on the Boat image with moderate noise corruption(σ=20).(a)Original image;denoised images by(b)SAPCABM3D(PSNR=31.02dB,SSIM=0.82);(c)SR(PSNR=30.42dB,SSIM=0.80);(d)NCSR(PSNR=30.74dB,SSIM=0.81);(e)FSR(PSNR=32.53dB,SSIM=0.86).

Fig.10. Denoising performance comparison on the Barbara image with moderate noise corruption(σ=20).(a)Original image;denoised images by(b)SAPCA-BM3D(PSNR=31.97dB,SSIM=0.90);(c)SR(PSNR=30.92dB,SSIM=0.88);(d)NCSR(PSNR=31.72dB,SSIM=0.90);(e)FSR(PSNR=32.56dB,SSIM=0.92).

B.Comparison of Computational Efficiency

In this section,we discussed the computational cost of our FSR model in comparison to the SAPCA-BM3D algorithm and the sparse representation-based models(e.g.,SR,NCSR).To make a fair comparison,the FSR model and the sparse representation-based models used the same stopping scalar controlling the convergence of the iterative.All the experiments were implemented on a personal computer(Intel i7-4790 CPU,3.60GHz,16GB RAM)with MATLAB 8.3 on 64-bit Windows 8.The experiments were repeated 10 times,and the results were reported with the average running time values for different noise levelsσ=5,10,20,35,50.

The computational cost of the proposed FSR model with comparison to other competing methods is reported in Table III.We can see that the SAPCA-BM3D algorithm and the NCSR model are time-consuming.For the SAPCA-BM3D algorithm,there is little difference in running time among the five noise levels.Note that the running time is directly proportional to the size of the image:331.55s for the House image of size 256×256 and 1329.63s for the Lena image of size 512×512 atσ=5.And the NCSR model requires more time for image denoising when the noise level increases.By contrast,the running time for both FSR and SR model declines with the increasing of noise,because the seriously corruption of noisy images at heavy noise levelsσ=35,50,these models can only learn few image texture details during the dictionary learning stage and converge quickly.The FSR model is more than 100 times faster than the SAPCA-BM3D and is over 30times faster than other sparse representation-based models.Consequently,the running time of the FSR model is significantly reduced,and the FSR model exhibits the best computational ef ficiency among the four approaches.

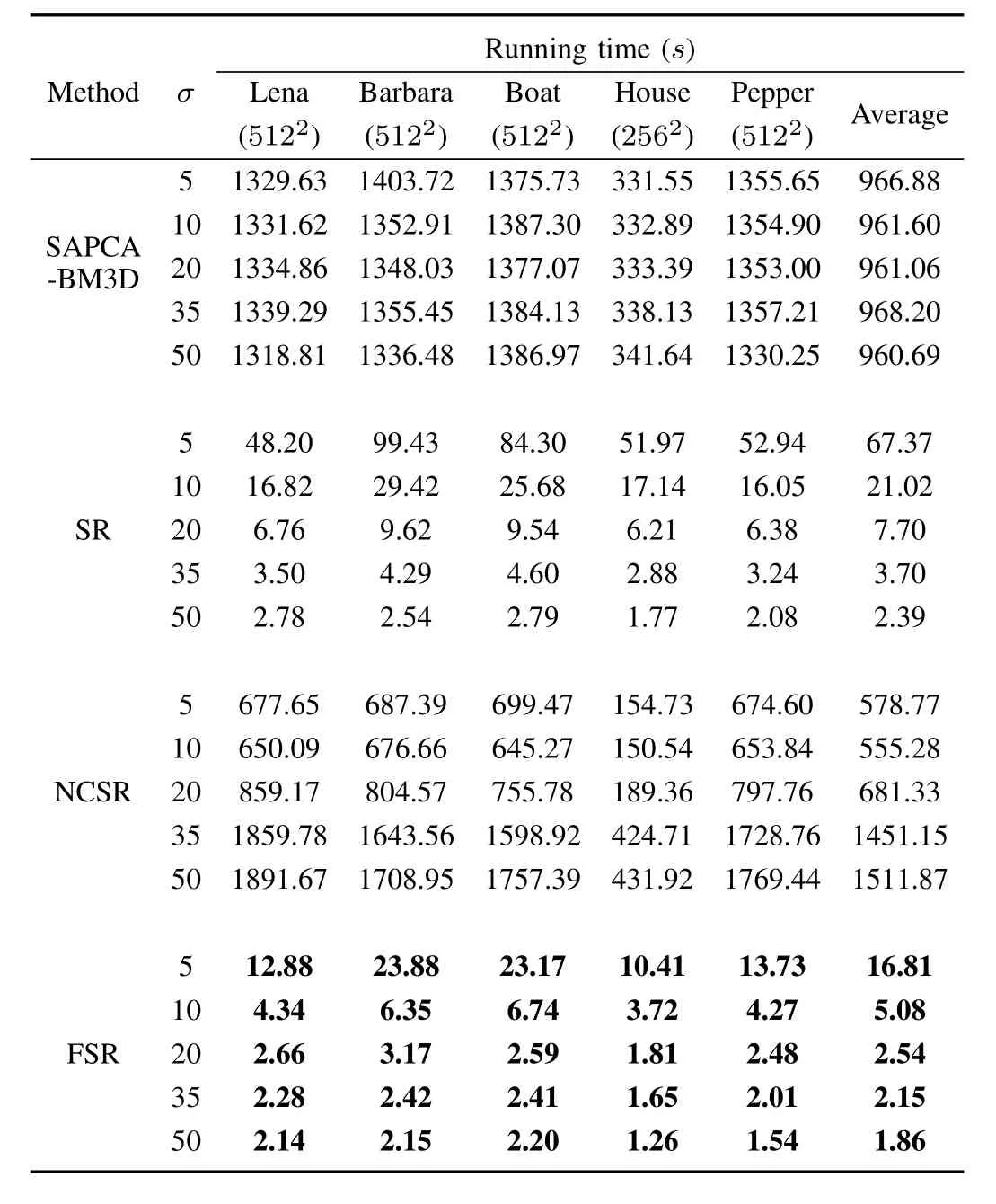
TABLE IIITIME CONSUMPTION RESULTS(IN SECONDS)FOR VARIOUS NOISY LEVELS OBTAINED BY THE SAPCA-BM3D,SR,NCSR AND FSR MODEL.THE LAST COLUMN PRESENTS THE AVERAGE RUNNING TIME RESULTS OVER ALL TEST IMAGES.THE BEST RESULT IS HIGHLIGHTED.

V.CONCLUSION

To obtain more accurate sparse coefficients and optimal dictionary,we presented a new model for image denoising called the fractional-order sparse representation(FSR)model.The proposed FSR model has been evaluated on the basis of five typical images with various noise levels.A series experimental results show that,in most cases,the FSR model significantly outperforms the SAPCA-BM3D and other two sparse representation-based models(e.g.,SR,NCSR).Furthermore,the FSR model performs with remarkable computational efficiency.Therefore,we can conclude that the proposed FSR model achieves state-of-the-art performance in terms of both denoising effectiveness and computational efficiency.However,the fractional-order parameters are learned from external images database.It remains unclear how to set fractional-order parameters automatically,which is out of scope of this paper and will lead to our future work.

[1]M.Afonso and J.M.Sanches,“Image reconstruction under multiplicative speckle noise using total variation,”Neurocomputing,vol.150,pp.200-213,Feb.2015.

[2]Z.G.Sun,S.C.Chen,and L.S.Qiao,“A general non-local denoising model using multi-kernel-induced measures,”Pattern Recognit.,vol.47,no.4,pp.1751-1763,Apr.2014.

[3]K.Dabov,A.Foi,V.Katkovnik,and K.Egiazarian,“BM3D image denoising with shape-adaptive principal component analysis,”inProc.Workshop on Signal Processing with Adaptive Sparse Structured Representation,Saint Malo,France,2009.

[4]Y.Romano and M.Elad,“Improving K-SVD denoising by postprocessing its method-noise,”inProc.20th IEEE Int.Conf.Image Processing,Melbourne,VIC,Australia,2013,pp.435-439.

[5]M.Elad and M.Aharon,“Image denoising via sparse and redundant representations over learned dictionaries,”IEEE Trans.Image Process.,vol.15,no.12,pp.3736-45,Dec.2006.

[6]A.M.Bruckstein,D.L.Donoho,and M.Elad,“From sparse solutions of systems of equations to sparse modeling of signals and images,”SIAM Rev.,vol.51,no.1,pp.34-81,Feb.2009.

[7]P.Chatterjee and P.Milanfar,“Clustering-based denoising with locally learned dictionaries,”IEEE Trans.Image Process.,vol.18,no.7,pp.1438-1451,Jul.2009.

[8]M.Zibulevsky and M.Elad,“L1-l2 optimization in signal and image processing,”IEEE Signal Process.Mag.,vol.27,no.3,pp.76-88,May2010.

[9]J.A.Tropp and S.J.Wright,“Computational methods for sparse solution of linear inverse problems,”Proc.IEEE,vol.98,no.6,pp.948-958,Jun.2010.

[10]X.Q.Zhang,M.Burger,X.Bresson,and S.Osher,“Bregmanized nonlocal regularization for deconvolution and sparse reconstruction,”SIAM J.Imag.Sci.,vol.3,no.3,pp.253-276,Jul.2010.

[11]A.Marquina and S.J.Osher,“Image super-resolution by TV-regularization and Bregman iteration,”J.Sci.Comp.,vol.37,no.3,pp.367-382,Dec.2008.

[12]M.Elad and M.Aharon,“Image denoising via learned dictionaries and sparse representation,”inProc.IEEE Computer Society Conf.Computer Vision and Pattern Recognition,New York,NY,USA,2006,pp.895-900.

[13]R.Rubinstein,T.Peleg,and M.Elad,“Analysis K-SVD:A dictionarylearning algorithm for the analysis sparse model,”IEEE Trans.Signal Process.,vol.61,no.3,pp.661-677,Feb.2013.

[14]J.C.Yang,Z.W.Wang,Z.Lin,S.Cohen,and T.Huang,“Coupled dictionary training for image super-resolution.”IEEE Trans.Image Process.,vol.21,no.8,pp.3467-78,2012.

[15]Y.B.Tang,N.Xu,A.M.Jiang,and C.P.Zhu,“Image denoising via sparse representation using rotational dictionary,”J.Electron.Imag.vol.23,no.5,Article ID 053016,Oct.2014.

[16]W.S.Dong,L.Zhang,G.M.Shi,and X.Li,“Nonlocally centralized sparse representation for image restoration,”IEEE Trans.Image Process.,vol.22,no.4,pp.1620-1630,Apr.2013.

[17]W.S.Dong,G.M.Shi,Y.Ma,and X.Li,“Image restoration via simultaneous sparse coding:Where structured sparsity meets Gaussian scale mixture,”Int.J.Comp.Vis.,vol.114,no.2-3,pp.217-232,Sep.2015.

[18]N.He,J.B.Wang,L.L.Zhang,and K.Lu,“An improved fractionalorder differentiation model for image denoising,”Signal Process.,vol.112,pp.180-188,Jul.2015.

[19]Y.F.Pu,J.L.Zhou,and X.Yuan,“Fractional differential mask:a fractional differential-based approach for multiscale texture enhancement,”IEEE Trans.Image Process.,vol.19,no.2,pp.491-511,Feb.2010.

[20]S.Larnier and R.Mecca,“Fractional-order diffusion for image reconstruction,”inProc.2012 IEEE Int.Conf.Acoustics,Speech and Signal Processing,Kyoto,Japan,2012,pp.1057-1060.

[21]Y.H.Yuan,Q.S.Sun,and H.W.Ge,“Fractional-order embedding canonical correlation analysis and its applications to multi-view dimensionality reduction and recognition,”Pattern Recognit.,vol.47,no.3,pp.1411-1424,Mar.2014.

[22]G.H.Golub and C.F.Van Loan,Matrix Computations.Baltimore:Johns Hopkins University Press,1996.