Operator-Based Robust Nonlinear Control for SISO and MIMO Nonlinear Systems With PI Hysteresis

Shuhui Bi,,Lei Wang,Shengjun Wen,and Mingcong Deng,Senior

I.INTRODUCTION

SMART actuators,such as piezoceramic and magnetostrictive actuators,are widely used in experimental investigation and manipulation of chemical,material,physical processes and so on due to their variety of advantages.However,such actuators generally exhibit hysteresis effects in their output responses,which may induce undesirable inaccuracies or oscillations,severely degrades system performance and decreases the system response due to the multi-values,nonsmooth and non-memoryless features of the hysteresis.For the treatment of the hysteresis,many efforts have been made in[1]-[7].Until now,the study on nonlinear systems with nonsmooth nonlinearities by traditional control methods is insufficient,and thus require development of effective approaches[5]-[10].Therefore,a general control framework of dynamical systems in the presence of hysteresis nonlinearities is still a challenging task[11]-[13].

For dealing with hysteresis,generally the first step is to develop mathematical models that are sufficiently accurate to compensate hysteresis in controller design and are efficient enough to use in real-time applications.For addressing the hysteretic behaviour,many phenomenological models have been proposed to describe the hysteresis nonlinearity,such as Duhen model[2],Preisach model[7],Krasnosel’skii-Pokrovkii hysteresis[3],Prandtl-Ishlinskii(PI)hysteresis operator[2],Bouc-Wen differential model[4],etc.Such models have been widely applied for modeling and compensation of hysteresis effects[5],[11].Generally,modeling hysteresis nonlinearities is still a research hot spot and the reader may refer to[14]for a recent review.Moreover,the inverse of the hysteresis models,derived using numerical or analytical methods,has been widely suggested for compensating the hysteresis effects.In the above mentioned models,the Prandtl-Ishlinskii model is analytically-invertible,and it can be conveniently implemented as a feed forward compensator for mitigating effects of hysteresis nonlinearities.

Another problem is the control system design,that is,remedying the undesirable behaviors by designing effective control algorithms,such as hysteresis,nonlinearities,uncertainties and so on.To the author’s knowledge,operator based robust right coprime factorization approach is effective for controlling above behaviors,because of the fact that it provides a convenient framework in researching input-output stability problems and meets the prerequisites for practical control design[15]-[25],which uses the input-output time function model given by basic physical rules from the real system.In addition,the robustness against significant(constant and timevarying)uncertainties can be guaranteed based on one Bezout identity and an inequality condition[23].In summary,operator based robust right coprime factorization approach provides a relatively simple and convenient framework for robust control design of nonlinear uncertain systems.

In control practices,with the increasing requirements to deal with the complexities of modern technology,multi-input multi-output(MIMO)systems have more practical and wider applications than single-input single-output(SISO)systems.One important property of MIMO systems is that one single output is affected by multiple inputs,which generates difficulties in designing MIMO control system.In comparison with the results on control system design for SISO systems in the control literatures,there are fewer results available for MIMO nonlinear systems due to the complications and the difficulties in dealing with the coupling effects.By using operator based control methods,the robust control design of MIMO systems has been considered in[20].Moreover,for the MIMO system preceded by hysteresis,the control problem has been considered in[17].However,the hysteresis is considered as one part of the uncertainties,which limits the system performance very much.For avoiding the limitation,hysteresis should be controlled alone based on its properties.Through the analysis of the hysteresis model,generalized PI hysteresis given in[6]is con firmed suitable for operator based control system design due to its Lipschitz property and invertibility.Therefore,in this paper,the generalized PI hysteresis will be analyzed,and robust control for SISO and MIMO nonlinear uncertain systems preceded by hysteresis will be considered.

The remainder of the paper is organized as follows.In Section II,some relevant notes on operator theory are introduced.In Section III,operator based control system design for SISO and MIMO system with feed forward and feedback controller is proposed.A numerical example is done to support the theoretical analysis in Section IV and conclusion is drawn in Section V.

II.PRELIMINARIES AND PROBLEM STATEMENT

A.Preliminaries

LetXandYbe linear spaces over the field of real numbers,and letXsandYsbe normed linear subspaces,called the stable subspaces ofXandY,respectively,de fined suitably by two normed linear spaces under certain normXs={x∈X:‖x‖ ＜∞}andYs={y∈Y:‖y‖ ＜∞}.LetQ:X→Ybe an operator mapping fromXtoY,and denote byD(Q)andR(Q),respectively,the domain and range ofQ.Generally,an operator is said to be bounded input bounded output(BIBO)stable or simply,stable ifQ(Xs)⊆Ys.Otherwise,ifQmaps some inputs fromXsto the setYYs(if not empty),thenQis said to be unstable[21].

LetS(X,Y)be the set of stable operators mapping fromXtoY.Then,S(X,Y)contains a subset de fined by

Elements ofU(X,Y)are called unimodular operators.In this paper,the operators used are generalized Lipschitz operators de fined on extended linear space[23].The norm ofQis de fined as

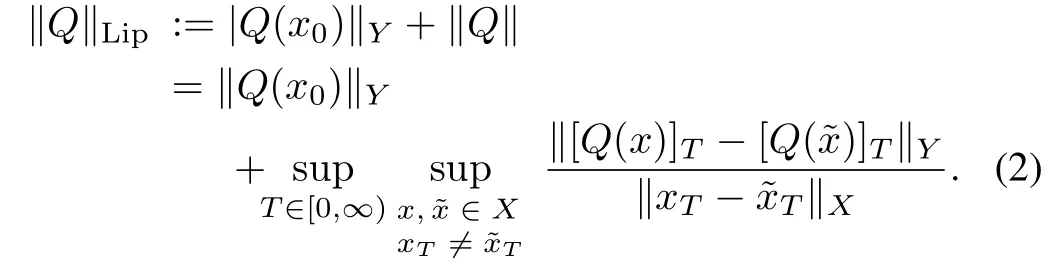
A normal operator based nonlinear feedback control system is shown in Fig.1,u∈Uandy∈Vare control input and plant output respectively,UandVare used to denote the input and output spaces of a given plant operatorP,i.e.,P:U→V.The given plant operatorP:U→Vis said to have aright factorization,if there exist a linear spaceWand two stable operatorsD:W→UandN:W→Vsuch thatDis invertible fromUtoW,andP=ND-1onU,where,the spaceWis called a quasi-state space ofP.In the right factorization ofP,D-1is unstable for the case ofPbeing unstable.That is,Nis the stable part of the plant,and the unstable part is included inD-1if the plant is unstable.Moreover,the factorization is said to be coprime,orPis said to have aright coprime factorization,if there exist two stable operatorsA:V→UandB:U→U,satisfying the Bezout identity

whereBis invertible.Usually,Pis unstable and(N,D,A,B)are to be determined.

Fig.1.A nonlinear feedback system.

It is worth to mention that the initial state should also be considered,that is,AN(w0,t0)+BD(w0,t0)=M(w0,t0)should be satisfied.In this paper,we selectt0=0 andw0=0.

In[21],the bounded input bounded output stability of the system has been proved under the condition(3).As for nonlinear system with perturbation,the robust control is shown as Fig.2[23],where,the nominal plant and plant perturbation arePand ΔP,respectively,and the overall plant˜Pis˜P=P+ΔP.The right factorization of the nominal plantPand the overall plant˜PareP=ND-1,P+ΔP=(N+ΔN)D-1,whereN,ΔN,andDare stable operators,Dis invertible,ΔNis unknown but the upper and lower bounds are known.Then the stability of the nonlinear feedback control system with perturbation can be guaranteed if

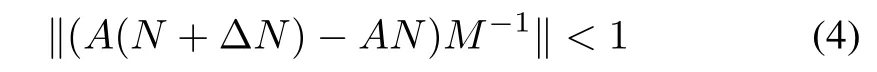
whereAandBsatisfy the Bezout identity(3).

Fig.2.A perturbed nonlinear feedback system.

B.Problem Statement

As for the MIMO nonlinear system with uncertain hysteresis,the robust control has been considered in[17],the control system was designed as Fig.3,where,the hysteresis was considered as one part of uncertainties which were controlled by the regulating operatorC.However,the detailed performance has not been considered yet,or if the influence of hysteresis is strong,then the method is not effective.Therefore,more detailed control design should be considered.

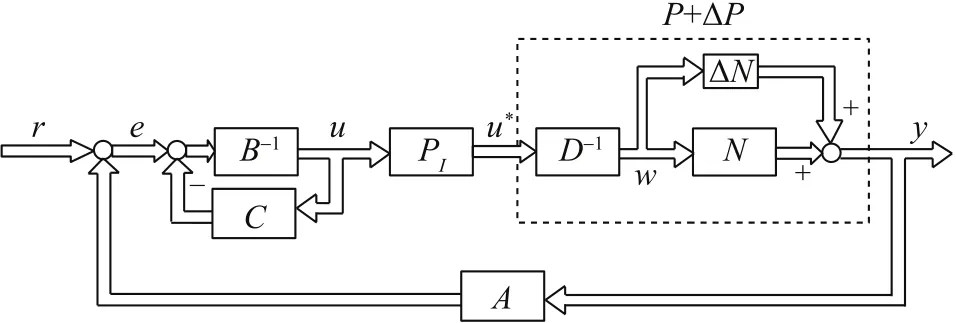
Fig.3.A control design for MIMO nonlinear system with hysteresis.

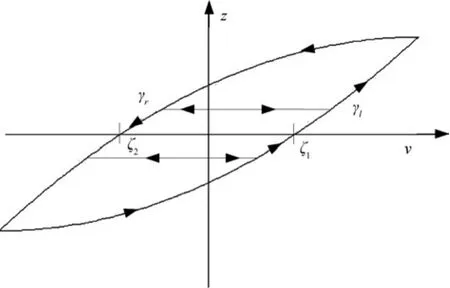
Fig.4.Input-output relationship of a generalized play operator.

III.CONTROL DESIGN FOR NONLINEAR SYSTEMS WITH GENERALIZED PRANDTL-ISHLINSKII HYSTERESIS

A.Prandtl-Ishlinskii Hysteresis Model

For predicting asymmetric input-output hysteresis,one generalized play operator was utilized to formulate a continuous generalized Prandtl-Ishlinskii model and to obtain its inverse model in[11],where,the generalized play operator for any inputu(t)∈Cm[0,T]is defined as

whereCm[0,T]is the space of the piecewise monotone continuous functions,0=t0＜t1＜···＜tN=Tare intervals in[0,T],such that the functionuis monotone on each of the subintervals[ti,ti+1],γrefers to the threshold value.

In detail,an increase in inputucauses the output of the generalized operatorzto increase along the curveγl,while a decrease in inputucauses the outputzto decrease along the curveγr,resulting in an asymmetric loop,which is shown as Fig.4,where,the curvesγlandγrare strictly increasing and continuous envelope functions withγl-γ≤γr+γ.Unlike the classical play operator,the generalized operator yields zero outputsz(t)=0 at two different valuesζ1andζ2of the increasing and decreasing inputsu(t),the difference in the magnitudes ofζ1andζ2allows for describing asymmetric hysteresis loops.The two constants can be obtained by the following relations:

Then,by the generalized play operatorSγ,the generalized Prandtl-Ishlinskii model is given as

pγ(γ)is the density function to describe the hysteresis nonlinearities.The thresholdγis applied in the Prandtl-Ishlinskii model as 0=r0＜r1＜···＜rn=R.and the inverse of generalized Prandtl-Ishlinskii model can be expressed in terms of envelope,density functions and play operator as follows(see[11]):

where the thresholdqis applied in the inverse Prandtl-Ishlinskii model as 0=q0＜q1＜···＜qn=Q.

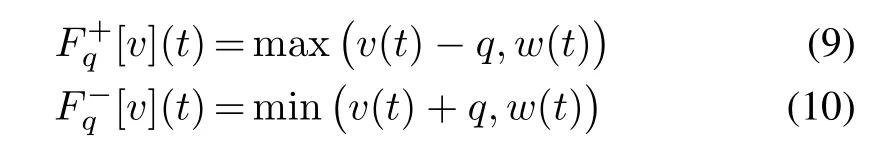
andψ(q)is the inverse initial loading curve and is de fined as

such that

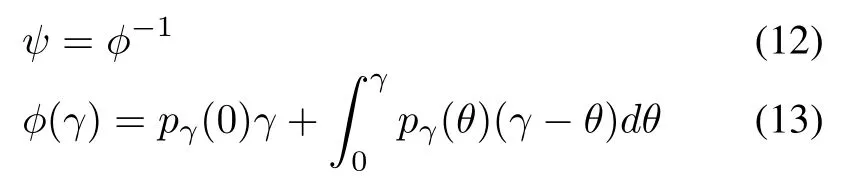
wheregq(0)is positive constant andqis the threshold of the inverse model.Consequently,the density function of the Prandtl-Ishlinskii model can be computed as follows:

and

The thresholdqis applied in the inverse Prandtl-Ishlinskii model as 0=q0＜q1＜···＜qn=Q.In summary,inverse generalized Prandtl-Ishlinskii model has the key properties that:1)is hysteresis operator;2)yields clockwise input-output curves;3)has Lipschitz continuity;4)is a monotone operator.That is,it can be applied in operator theoretic settings.

B.Robust Control for SISO System With Generalized PI Hysteresis

In[19],robust nonlinear control system design for SISO nonlinear system with generalized PI hysteresis was considered,and the control design with a feed forward controller is proposed as Fig.5,where,Φ is a generalized Prandtl-Ishlinskii hysteresis operator such thatu∗(t)= Φ(ud)(t),the real system plant isand the nominal plant isP,they have right factorization as=D-1=(N+ΔN)D-1andP=ND-1,respectively.ΔNis concerning with the unmodeled uncertainties,and its upper and lower bounds are known.A,BandFare operators to be designed,r∈U,ud∈U,w∈Wandy∈Vare the reference input,control input,quasi-state and system output,respectively.

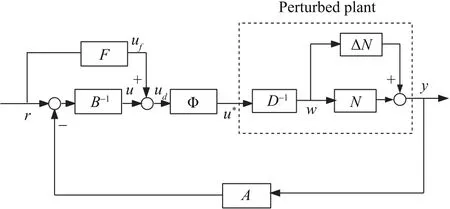
Fig.5.Proposed control design for nonlinear uncertain system with PI hysteresis.

In[16],the mismatch between the real plant and the nominal plant can be predicted by a prediction structure,which is denoted by ΔP∗and the desired mismatch operator is equivalent to the plant perturbation ΔP,namely,ΔP∗= ΔP.We assume that ΔP∗has right factorization as ΔP∗= ΔN∗D-1,and ΔN∗is bounded.As mentioned in[18],operatorNcan be divided into two parts,that is,N=Nu+Ns,whereNuis unimodular operator,Nsis stable and is as small as possible.Then,if the uncertainty part is relatively smaller thanNu,namely,

As pointed in last subsection,the generalized PI hysteresis model and its inverse are Lipschitz continuous,then,in operator theoretic settings,we can assume that the controllersAandBare designed satisfying the following conditions that

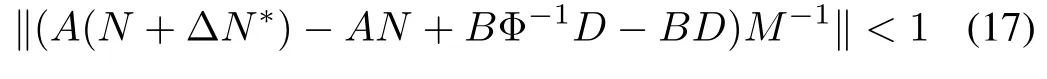
whereMis unimodular operator satisfying the Bezout identity(3).According to[23],condition(17)implies thatA(N+ΔN∗)+BΦ-1D=˜Mis unimodular operator.Then,ifBis linear,the system has that

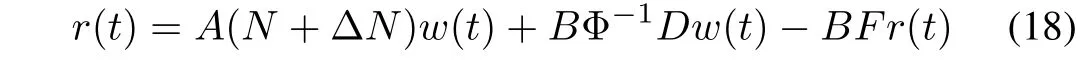
which implies

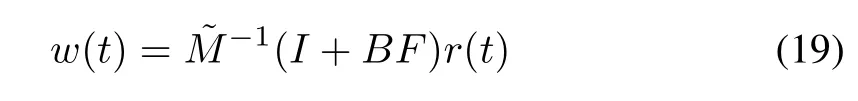
then the system can be rewritten as Fig.6.According to[23],ifFis stable,then the whole system is robustly stable due to the stability property of the operators˜MandF.

Fig.6.The equivalent system of Fig.5.

Theorem 1:As for the nonlinear system with hysteresis shown in Fig.5,ifA→IandF=Φ-1(P+ΔP∗)-1,then the output y(t)tracks the reference inputr(t).

Proof:Based on(19),the system has that

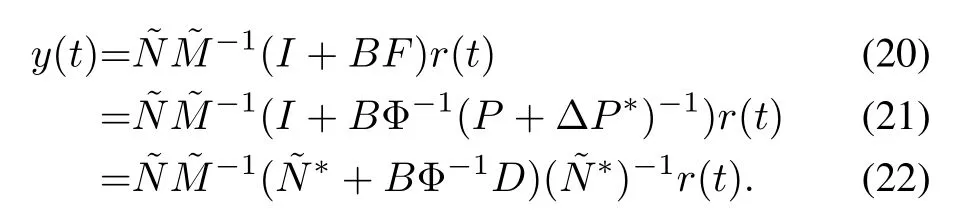
Remark:Due to the nonlinearity of system,the conditionA→Iensures unknown in fl uence in the feedback process due toAis nonlinear.The theorem also shows that operator control structure can be chosen as a general control structure,which indicates the universality of operator theoretic approach.

In this control design,prediction and modeling errors are inevitable,in order to realize perfect tracking performance,another tracking operator is added in a feedback loop,which is shown in Fig.7,whereTris a tracking operator,the part in dotted box is the stabilizing system

Fig.7.Tracking design.

Theorem 2:The error signale∗with the controllerTrcan be made arbitrarily small.That is,y(t)-r∗(t)can be made arbitrarily small byt≤Tlarge enough,where,controllerTris designed so that the open loopin Fig.7 consists of an integrator in cascade with a systemPTand satis fies the following conditions:

1)For alltin[0,T],Tris stable,andPT(e∗)/=K1＞0 asT/=t/=t1/=0,e∗＞0.

2)PTr(0)=0.

3)‖PTr(x)-PTr(y),t‖≤hRt0‖x-y,t1‖dt1,for allx,yinVsand for alltin[0,T],his any constant and is the gain ofPTin the first norm,where the norm ofxrestricted to any interval[0,T]will be denoted by‖x,t‖.

The proof process is similar as in[23],which is omitted here.

C.Robust Control for MIMO System With Generalized PI Hysteresis

In this part,the robust control for MIMO system with generalized PI hysteresis is considered.Based on the control design for SISO system,combining with the coupling effects,the control design for MIMO system is given as Fig.8,where,the nominal plants and perturbed plants arePand ΔP.Let input space,output space,quasi-state space be U,V,W,and plantsP:U→V,and let the input,error,control input,quasi-state and plant output ber=(r1,r2,...,rn)∈U,e=(e1,e2,...,en)∈U,u=(u1,u2,...,un)∈U,w=(w1,w2,...,wn)∈W andy=(y1,y2,...,yn)∈V,respectively.A=(A1,A2,...,An),B=(B1,B2,...,Bn)are controllers to be designed.

Fig.8.Control design for MIMO system with hysteresis.

Different from our previous study,for the known coupling effects,we do not use new defined operators to describe them,because the known coupling effects just exist in the model.Then,we assume that the coupling effects exist in the part ofDsuch that

and ΔN=(N1,N2,...,Nn)are unknown but their upper and lower bounds are known.According to the proposed control design for SISO system preceded by hysteresis,ifBiis linear,then the system has that

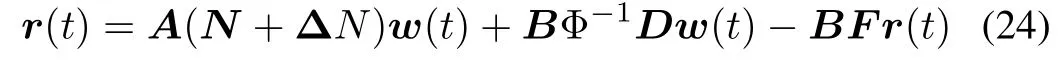
because of the coupling effects,the system can not use the results of last subsection directly.Without considering the effects of hysteresis,the robust stability was considered in[20].Based on the results,we redraw the system control design as Fig.9.Lemma 1:IfRiis linear and

Fig.9.New control design for MIMO system with hysteresis.

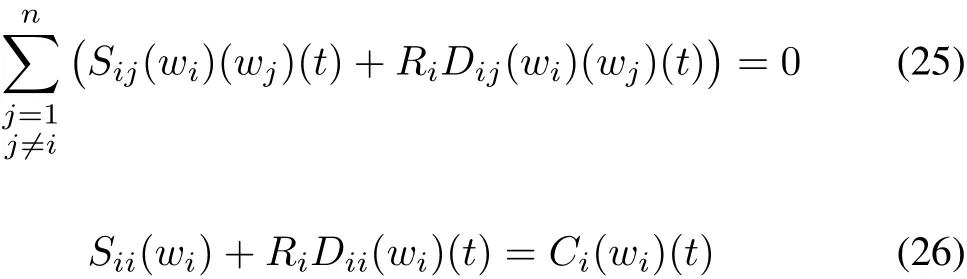
then the plant is decoupled provided thatCiis invertible and stable[19].

Based on the above conditions,the system can be decoupled,and the output tracking conditions can be realized by Theorem 2.Then,in the following,we will consider the robust condition of the MIMO system with hysteresis.

Generally,by operator based system control design,there is a relation between the input and quasi-state,that is,if robust right coprime factorization condition is satisfied,the relation can be written as

which follows

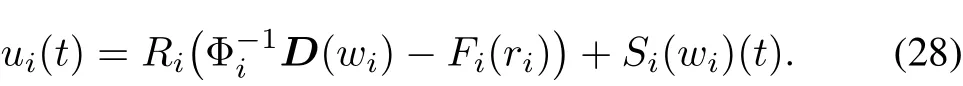
According to the proposed control design of SISO system with hysteresis,the feed forward controllerFcan be designed as

it follows that the coupling effects inDand the hysteresisφican be canceled byF,that is

In brief,we can chooseR=I,then the system can be rewritten as Fig.10.

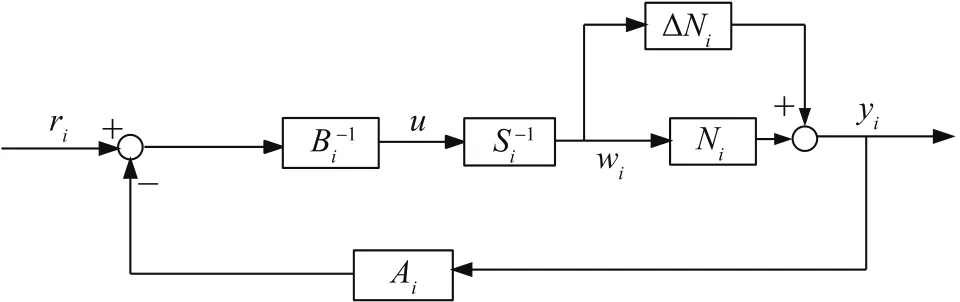
Fig.10. Equivalent system of Fig.9.

Remark:Owing to the the coupling effects and nonlinearities,Fig.9 cannot be redrawn as Fig.6.

Then,in the same manner of[16],the controllers are designed as

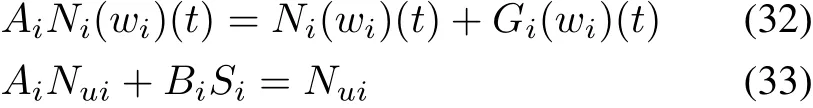
whereNi=Nui+Nsi,Nuiis unimodular,andNsiis stable such that

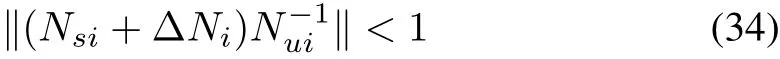
then

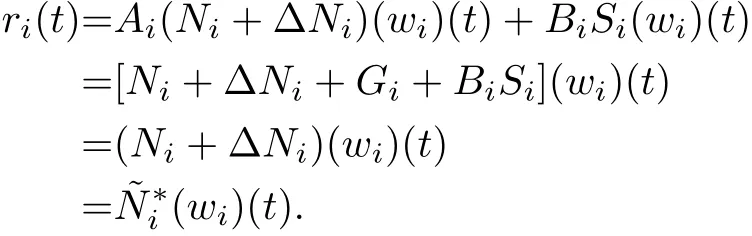
That is,(27)is realized.At the same time,the output tracking performance can be realized because of the fact thatyi(t)=˜N∗i(wi)(t).In summary,the stability can be guaranteed by the following theorem.

Theorem 3:As for the nonlinear system with hysteresis shown in Fig.9,the system is robustly stable and the outputy(t)tracks the reference inputr(t)provided that the conditions(29),(32)-(34)are satisfied.

Remark:The proposed operator based control structure can deal with the hysteresis effects by using the model and its inverse even the model is not accurate enough,that is one merit of the usage of operator theoretical based control method.Another merit of this work is that we take uncertainty,coupling effects and hysteresis into consideration synthetically.As for the interval of hysteresis,namely,the bounds of the hysteresis model will be considered in the future work.

IV.SIMULATION EXAMPLE

In this section,the effectiveness of the proposed design scheme is demonstrated by a mathematical simulation.For simulation,two-input two-output unstable nonlinear plant preceded by hysteresis is considered.The nominal plants are selected as follows:

where

andZiis parameter.

We can find that the two-input two-output model is a nonlinear system with coupling effect.In this paper,the right factorizing way is selected as

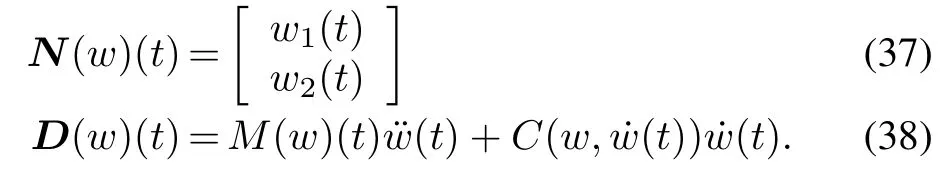
As for the generalized PI model,assume that two hysteresis are same,and the linear envelope functions are chosen to construct the asymmetric hysteresis loops,de fined as follows:

Figs.11 and 12 show the simulation results obtained from the outputs of the generalized PI model and its inverse,respectively.The results show asymmetry in the minor and major loops in the outputs of both the models.Furthermore,the output-input loops in the models exhibit opposite direction.

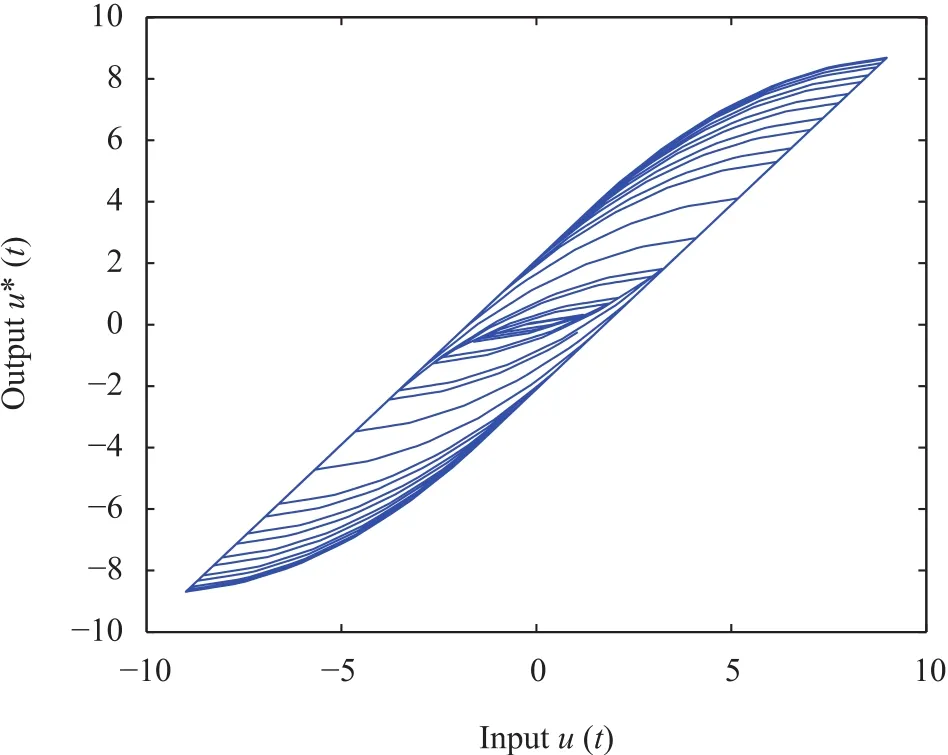
Fig.11. Response characteristics of the generalized PI model.

Fig.12. Response characteristics of the inverse generalized PI model.

In the proposed control design,controllerFincludes the inverse ofP+ΔP,we assume that the predicted mismatch can be described as ΔNi(wi)=δiwi,whereδi=0.5 such that|δi|＜1.In this example,Pis invertible,and then we can assume that the prediction error is equivalent to the uncertainty,then according to the proposed design scheme,the hysteresis and the coupling effects are canceled by the constructed feed forward controllerF,and the controllerSican be selected as a linear operator(1/2)I,andBi=I,Ai(Ni(wi))=Ni(wi)+Gi(wi),whereGi(wi)=-BiSi(wi),then it satisfies the proposed condition due to the fact that

In this example,the structural parameters are selected asZ1=0.507,Z2=0.1775,andZ3=0.2530,respectively.Since there are errors in obtaining the structure parametersZi.In simulation,the reference inputs are chosen asθ1(t)=sin(πt)/2,θ2(t)=sin(πt),then the simulation results are given in Figs.13-15.Fig.13 shows the plant output of the system with control.By the proposed control design scheme,the control input is shown in Fig.14,and tracking error is drawn by Fig.15.The simulation results demonstrate the perfect tracking performance of the proposed method.

Fig.13. Tracking responses.

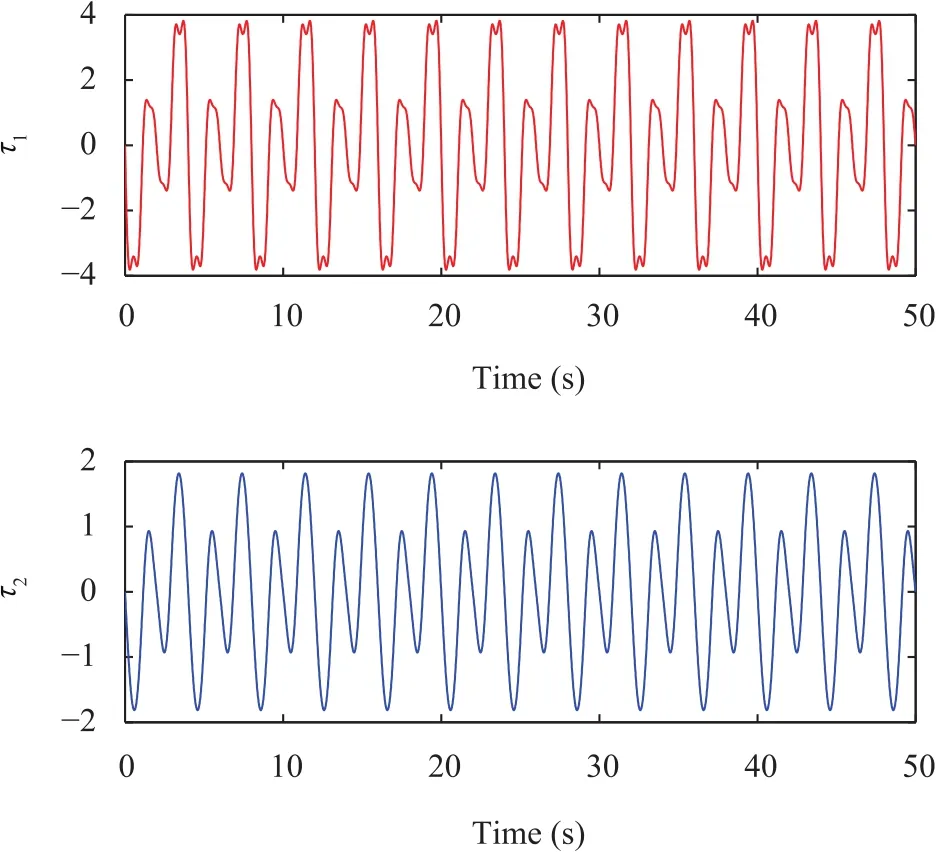
Fig.14. Control inputs.

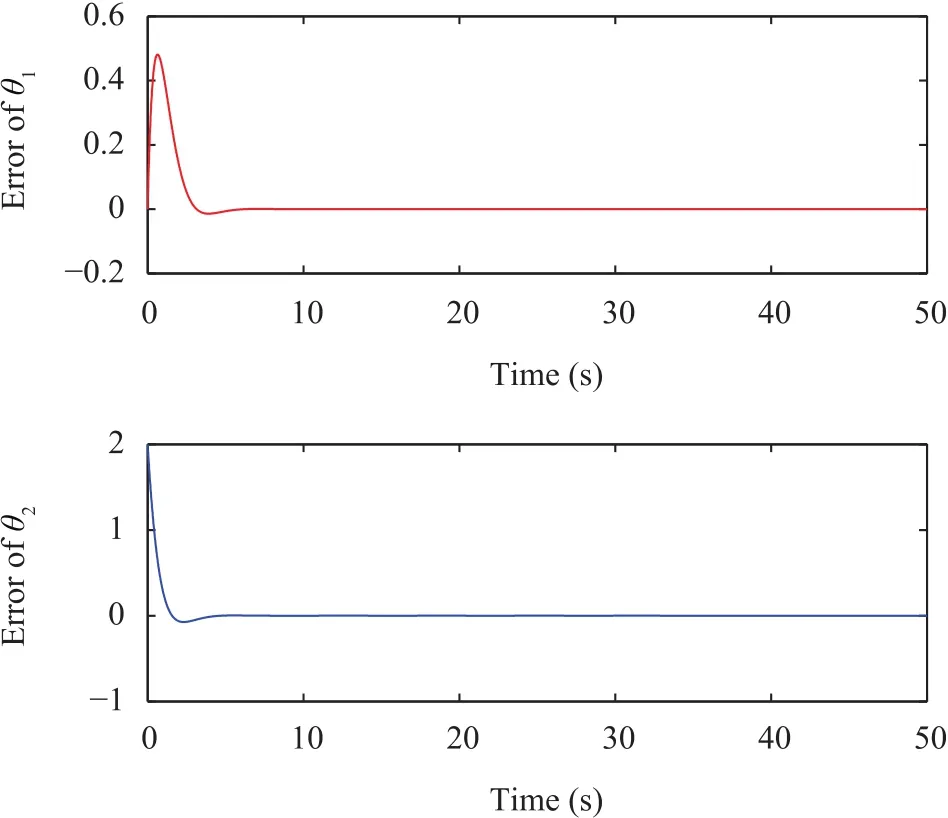
Fig.15. Tracking errors.

V.CONCLUSION

Operator based robust control of SISO and MIMO nonlinear systems with hysteresis is considered in this paper.By using operator based robust right coprime factorization approach,control design combining feed forward and feedback controllers are proposed respectively.Moreover,the sufficient conditions for the system to be robustly stable and guaranteed output tracking performance are proposed.Finally,the effectiveness of the proposed method is con firmed through numerical simulations.

[1]M.Brokate and J.Sprekels,Hysteresis and Phase Transitions.New York:Springer-Verlag,1996.

[2]J.W.Macki,P.Nistri,and P.Zecca,“Mathematical models for hysteresis,”SIAM Rev.,vol.35,no.1,pp.94-123,Mar.1993.

[3]M.A.Krasnosklskii and A.V.Pokrovskii,Systems with Hysteresis.Moscow,Russia:Nauka,1983.

[4]M.Rakotondrabe,“Bouc-Wen modeling and inverse multiplicative structure to compensate hysteresis nonlinearity in piezoelectric actuators,”IEEE Trans.Automat.Sci.Eng.,vol.8,no.2,pp.428-431,Apr.2011.

[5]G.Tao and F.L.Lewis,Adaptive Control of Nonsmooth Dynamic Systems.New York:Springer-Verlag,2001.

[6]C.Y.Su,Y.Stepanenko,J.Svoboda,and T.P.Leung,“Robust adaptive control of a class of nonlinear systems with unknown backlash-Like hysteresis,”IEEE Trans.Automat.Control,vol.45,no.12,pp.2427-2432,Dec.2000.

[7]R.V.Iyer,X.B.Tan,and P.S.Krishnaprasad,“Approximate inversion of the Preisach hysteresis operator with application to control of smart actuators,”IEEE Trans.Automat.Control,vol.50,no.6,pp.798-810,Jun.2005.

[8]B.B.Ren,S.S.Ge,C.Y.Su,and T.H.Lee,“Adaptive neural control for a class of uncertain nonlinear systems in pure-feedback form with hysteresis input,”IEEE Trans.Syst.Man Cybern.B Cybern.,vol.39,no.2,pp.431-443,Apr.2009.

[9]Y.J.Liu,S.C.Tong,C.L.P.Chen,and D.J.Li,“Neural controller design-based adaptive control for nonlinear MIMO systems with unknown hysteresis inputs,”IEEE Trans.Cybern.,vol.46,no.1,pp.9-19,Jan.2016.

[10]Y.J.Liu and S.C.Tong,“Adaptive fuzzy control for a class of unknown nonlinear dynamical systems,”Fuzzy Sets Syst.,vol.263,pp.49-70,Mar.2015.

[11]M.Al Janaideh,S.Rakheja,and C.Y.Su,“An analytical generalized prandtl-ishlinskii model inversion for hysteresis compensation in micropositioning control,”IEEE/ASME Trans.Mech.,vol.16,no.4,pp.734-744,Aug.2011.

[12]X.K.Chen and T.Ozaki,“Adaptive control for plants in the presence of actuator and sensor uncertain hysteresis,”IEEE Trans.Automat.Control,vol.56,no.1,pp.171-177,Jan.2011.

[13]J.Zhou,C.Y.Wen,and T.S.Li,“Adaptive output feedback control of uncertain nonlinear systems with hysteresis nonlinearity,”IEEE Trans.Automat.Control,vol.57,no.10,pp.2627-2633,Oct.2012.

[14]L.Chua and S.Bass, “A generalized hysteresis model,”IEEE Trans.Circuit.Theoryvol.19,no.1,pp.36-48,Jan.1972.

[15]A.Ban´os,“Stabilization of nonlinear systems based on a generalized Bezout identity,”Automatica,vol.32,no.4,pp.591-595,Apr.1996.

[16]S.H.Bi and M.C.Deng,“Operator-based robust control design for nonlinear plants with perturbation,”Int.J.Control,vol.84,no.4,pp.815-821,Apr.2011.

[17]S.H.Bi,M.C.Deng,L.Wang,and Y.G.Zhao,“Operator-based robust control for MIMO non-linear systems with uncertain hysteresis,”Int.J.Adv.Mech.Syst.,vol.4,no.5-6,pp.212-220,Jan.2012.

[18]S.Bi,M.Deng,and S.Wen,“Operator-based output tracking control for non-linear uncertain systems with unknown time-varying delays,”IET Control Theory Appl.,vol.5,no.5,pp.693-699,Mar.2011.

[19]S.H.Bi,X.L.Wang,J.H.Zheng,and L.Wang,“Operator-based robust nonlinear control for system with generalized PI hysteresis,”inProc.2014 Int.Conf.Advanced Mechatronic Systems,Kumamoto,Japan,2014,pp.19-42.

[20]S.H.Bi,Y.F.Xiao,X.J.Fan,and M.C.Deng,“Operator-based robust decoupling control for MIMO nonlinear systems,”inProc.11th World Congr.Intelligent Control and Automation,Shenyang,China,2014,pp.2602-2606.

[21]G.R.Chen and Z.Z.Han,“Robust right coprime factorization and robust stabilization of nonlinear feedback control systems,”IEEE Trans.Automat.Control,vol.43,no.10,pp.1505-1509,Oct.1998.

[22]M.C.Deng,A.Inoue,and Y.Baba,“Operator-based non-linear vibration control system design of a fl exible arm with Piezoelectric actuator,”Int.J.Adv.Mech.Syst.,vol.1,no.1,pp.71-76,Jan.2008.

[23]M.C.Deng,A.Inoue,and K.Ishikawa,“Operator-based nonlinear feedback control design using robust right coprime factorization,”IEEE Trans.Automat.Control,vol.51,no.4,pp.645-648,Apr.2006.

[24]S.H.Bi,M.C.Deng,and Y.F.Xiao,“Robust stability and tracking for operator-based nonlinear uncertain systems,”IEEE Trans.Automat.Sci.Eng.,vol.12,no.3,pp.1059-1066,Jul.2015.

[25]S.H.Bi,L.Wang,Y.G.Zhao,and M.C.Deng,“Operator-based robust control for nonlinear uncertain systems with unknown backlash-like hysteresis,”Int.J.Control Automat.Syst.,vol.14,no.2,pp.469-477,Apr.2016.