Constructing Multicast Routing Tree for Inter-cloud Data Transmission:An Approximation Algorithmic Perspective

Jun Huang,,Shihao Li,and Qiang Duan,

I.INTRODUCTION

CLOUD computing allows a pool of abstracted,virtualized,and scalable computing resources to be delivered on demand as services over the Internet.The past decade has witnessed rapid development in cloud computing technologies and numerous cloud services have been deployed for supporting a wide variety of applications.The traditional cloud service model,where a client utilizes a single cloud data center for access services,is facing some challenges,such as reliability and availability of a single data center,elastic service provisioning for better service quality,and the potential vendor lock-in issue.Usage of multiple cloud data centers to forms an Inter-cloud environment for further enhancing cloud service provisioning has attracted research interest from both academia and industry.

Networking plays a crucial role in cloud computing especially in an inter-cloud environment,where data communications among data centers located at different geographical sites form the foundation of inter-cloud federation.Due to the very dynamic interactions among data centers for supporting diverse service provisioning,the networking system in an intercloud environment form a quite complex system.Data transmissions required for inter-cloud federation in the complex inter-cloud networking system are often point-to-multipoints,for example multimedia content delivery services offered by cloud providers require high performance data transmission from a single data source to multiple destinations.Therefore inter-cloud service provisioning calls for more effective and efficient multicast routing mechanisms in complex networking systems.

Multicast is a networking technology that enables packets to be simultaneously forwarded to multiple destinations from a single data source.Traditional multicast routing techniques implement routing procedures mainly by using the minimum-hop constraint or the shortest path tree(SPT)as the measurement[1].Compared to traditional network applications,multimedia inter-cloud services bring in more challenging requirements such as mass data traf fic,low latency,low packet loss rate,and long duration.Therefore,multicast routing needs to fully consider these new challenging issues.

Constructing multicast trees is a common solution to multicast routing problems.Real-time monitoring and controlling of quality-of-service(QoS)metrics is difficult in the conventional IP-based networks due to the complexity of network control and management.Therefore,multicast algorithms designed for such networking scenarios mainly consider constructing multicast trees with single QoS metric,typically data transmission delay or available bandwidth.Inter-cloud communications between data centers often leverage the software-defined networking technologies,which decouple network control functions from data forwarding operation thus enabling simplified network control with enhanced network manageability.Multicasting algorithms in an inter-cloud networking environment should not only consider more QoS metrics but also be adaptive to the dynamic changes in such QoS metrics.Therefore,the capability of constructing multicast trees with multiple QoS constraints in real-time becomes an important requirement for multicast routing algorithms in inter-cloud networks.

In general,there are three different types of the multicast trees:source-based SPT,Steiner tree,and center-based tree.The source-based SPT and the Steiner tree are the two representative ones out of three.A key feature of SPT is its smallest total path weight from the source node to all destination nodes,while Steiner tree minimizes the total weight from the source node to all destination nodes.Since the latter type of tree is known to be NP(non-deterministic polynomial-time)-complete[2],it has attracted considerable research interests during the last decade.Takahashi and Matsuyama[3]proposed a minimum tree-based greedy heuristic to compute a multicast tree whose cost is within twice the cost of the corresponding Steiner tree.Zelikovsky[4]improved this result to about 1.83 times the cost of a Steiner tree.Recently Robins and Zelikovsky[5]presented a new polynomial-time heuristic that achieves the best-known approximation ratio of 1.55 for general graphs.Unfortunately,these works were conducted in the general arbitrarily weighted graphs;and,when viewed from a practical network-studying perspective,the behavior suggested by those arbitrary weights might not occur in real-world networks.

Currently there is a large body of research efforts on seeking an optimized SPT.Bharath-Kumar and Jaffe[6]investigated the minimization of both cost and delay through assuming that the cost and delay functions are the same in a network.Khulleret al.developed a simple polynomial-time algorithm in[7]to find a spanning tree that simultaneously approximates a shortest-path tree and a minimum spanning tree.Parsa and others of[8]presented an algorithm for constructing minimum-cost multicast trees which is based on a feasible search optimization strategy that starts with the minimumdelay multicast tree and monotonically decreases the cost by iterative improvements of the delay-bounded multicast tree.Xue[9]extended the idea of[10]for balancing minimum spanning trees and shortest path trees to compute impressive approximations to delay-constrained multicast trees.This algorithm was proven to be able to deliver an outstanding approximation ratio when every edge has the same cost and delay values.

While the above mentioned works mainly focused on constructing an SPT with cost and delay constraints,the case withKconstraints(K≥2)has received limited attention.Multicast routing withKconstraints is a challenging issue and deserves thorough investigations since the newly emerged services require the constructed multicast trees satisfy three or even more QoS requirements.We have presented two approximation algorithms forK-constrained multicast routing problem in our recent work[11],but the effectiveness of those algorithms can still be improved.In this paper,we target on resolving this issue based on[11]by designing a more ef ficient algorithm.Our contributions are summarized as follows.

1)We formulate the multi-constrained multicast routing problem and propose a novel and fast algorithm leveraging the entropy technique to address the problem.

2)We analyze the performance of the proposed algorithm.The theoretical results show that the proposed algorithm has lower time complexity than that of a current representative existing algorithm.

3)We conduct intensive numerical experiments to validate the performance of the algorithm.Obtained experimental results indicate that our algorithm outperforms the previous existing algorithm in terms of both speed and accuracy.

The rest of this paper is organized as follows.Section II formally formulates the problems and notations.The proposed algorithm for multi-constrained multicast routing and its relevant analysis are presented in Section III.The experimental results are given in Section IV to examine the efficiency of the proposed algorithm.Section V concludes this paper.

II.PRELIMINARIES

In this section we formulate the problems and define the notions that will be used throughout the paper.Most of definitions and mathematical notations are inherited from[11].

A communication network in an inter-cloud context can be represented by a connected and weighted graphG(V,E,w1,...,wK),whereVis the set ofnvertices,Eis the set ofmedges.Each edge hasKindependent additive weights1We only consider the additive constraint since the edges with concave constraint can be erased beforehand.w1,...,wK,in whichwk(e)≥0 is thekth weight of edgee,∀e∈E,1≤k≤K.LetTbe a multicast routing tree inG(V,E).Denotewk(T)as the sum of thekth weights on edges ofT,then

Definition 1:Multicast tree(MT).Given a source nodes∈Vand a set of destination nodesD⊆V,(s/∈D),multicast treesT(s,D)are subgraphs ofGwhose root node issand whose leaf nodes form the subsets ofD.

For any pair of nodesu,v∈T,we usep(u,v,T)to denote the unique path fromutov,andwk(p(u,v,T))denotes the sum ofkth weight ofp(u,v,T).

De finition 2:Minimum Steiner tree(MST).WhenK=1,an MST is a multicast tree inT(s,D)whose weight is minimum among all multicast trees.

De finition 3:Shortest path tree(SPT).WhenK=1,an SPT is a multicast tree inT(s,D)wherew1(p(s,v,T))is the smallest for every nodev∈D.

An SPT can be calculated inO(m+nlogn)time,while an MST cannot be computed in polynomial time[2].This paper mainly focuses on finding an optimal multicast tree with multiple constraints.Specifically,letW1,...,WKbe theKQoS constraints.

Problem 1:Multi-constrained multicast tree(MMT).The problem of MMT is to find a multicast tree inT(s,D)such thatwk(T)≤Wk,1≤k≤K.

A multicast tree that satisfieswk(T)≤Wk,1≤k≤Kis said to be a feasible tree.We use{Tf}to denote all the feasible trees inG(V,E).For each feasible treeTi∈{Tf},there exists a smallestθi∈(0,1]such thatwk(Ti)≤θi·Wk,1≤k≤K.

Problem2:Multi-constrained optimal multicast tree(MOMT).The problem of MOMT is to find a multicast treeToptamong all feasible trees{Tf}inG(V,E)and the smallest value ofθamong allθisuch thatwk(Topt)≤θ·Wk,1≤k≤K.

Since MOMT is a combination of the MST problem and the multi-constrained path(MCP)problem,we claim that the problem of MOMT is NP-complete.This is due to the fact that forD={d}the MOMT reduces to the MCP,which is already proved to be NP-complete forK≥2 additive parameters[12].On the other hand,for the caseK=1,MOMT reduces to the MST,which is also proved to be NP-complete[2].Therefore,the NP-completeness of MOMT can be seen immediately.The objective of this paper is to find an algorithm to deal with this problem.

Table I lists the frequently used notations in this paper.

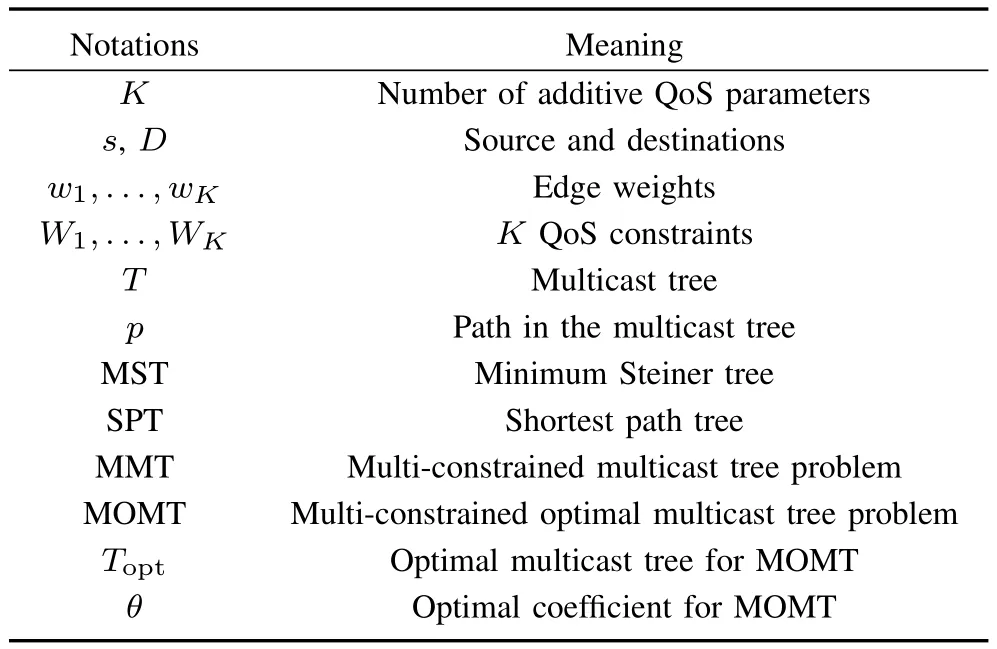
TABLE IFREQUENTLY USED NOTATIONS

III.ALGORITHM DESCRIPTION AND ANALYSIS

We first present an entropy-based weight aggregation algorithm,then,on the basis of it,we propose an algorithm for establishing the multicast routing tree.Time complexity and approximation analysis are also given for this algorithm in this section.

A.Entropy-based Weight Aggregation

Entropy plays a vital role in multi-criteria decision areas and is widely used for criteria aggregation[13].Using this technology,the multi-criteria decision problem can be naturally transformed to be a single-criterion decision problem.Here,we adopt the entropy technology to reduce the multiconst rained multicast routing problem.An entropy-based algorithm for weight aggregation,termed EWA,is presented in Algorithm 1.

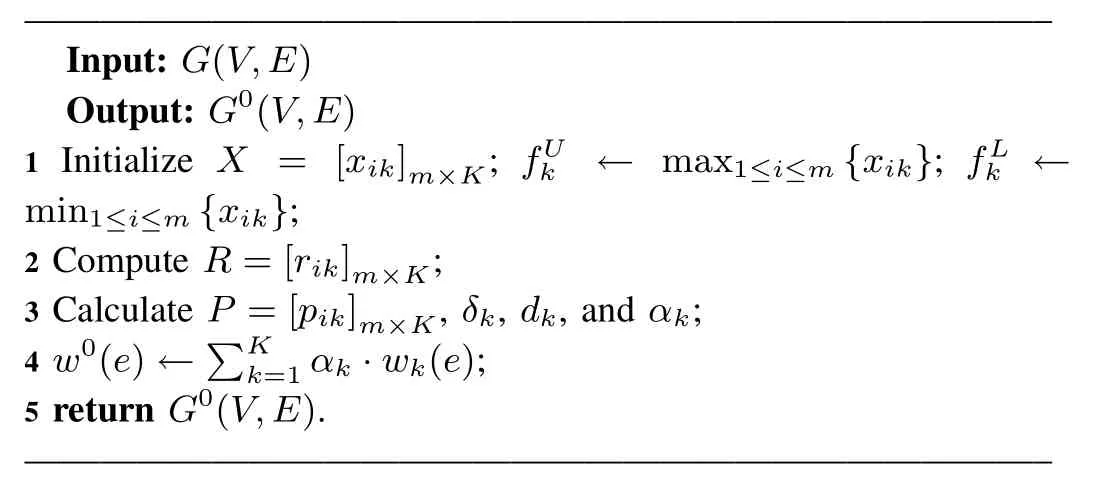
Algorithm 1 EWA

In the first step,EWA calculates the matrixXby observingG(V,E)where the elementxikofXdenotes thekth weight of theith edge inG(V,E).In the second step,two parameters are obtained,sayfUkandfLk.Both of them are used in the next step to calculate the matrixR.Since the type of weights on each edge could be either positive or negative[14],we applyfUkandfLkto calculate different types of weights,that is

Obviously 0≤rik≤1,the normalized matrixP=[pik]m×Kcan be computed by

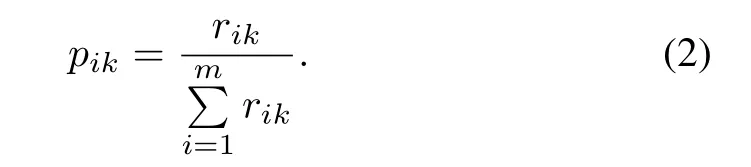
Thenδk,dk,andαkare calculated by

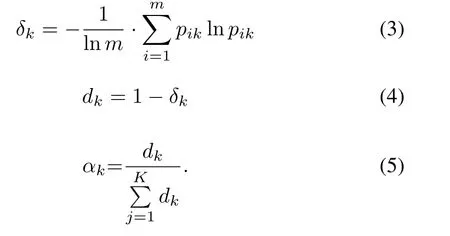
Withαk,EWA immediately obtainsw0(e)in Step 5.Then a graphG0(V,E),which is associated with only one weightw0(e)of each edge,is returned in the last step.

We now present the algorithm to solve the MOMT problem by using the EWA in the following.

B.Algorithm Description

The proposed algorithm,termed FAMOUS(a fast multicon-strained multicast routing algorithm),is given in Algorithm 2,in which the EWA is called in the first step for transforming the problem to be a simple one.The remaining steps of FAMOUS follow the same philosophy of the shortest path tree,where

Adj[u]:the adjacent nodes ofu;

Plen[u]:the length of the shortest path fromstou;

Tist[u]:the shortest length fromuto the current treeTm;

Parent[u]:the parent node ofu;

w0(es,a):the aggregated weight of edge(s,a).

It is interesting to notice that the obtained multicast treeTmmay be infeasible since the aggregation of the weights leads to some weight which is likely to exceed the constraint.To remedy this situation,we employ a request- filtering process[15]executed in advance to assure that the request,i.e.,the constraint is valid.Thus,it is guaranteed thatTmis a feasible multicast tree.

Fig.1 provides an illustrative example of the execution of FAMOUS,where s is the source and d1,d2,d3 are destinations.Fig.1(a)shows the original graph G(V,E)and the weights associated with each edge.Fig.1(b)gives the graph G0(V,E)with the aggregated weight on each edge obtained by EWA.Fig.1(c)depicts the process of adding the destination node d1 to the multicast tree.It seems that Fig.1(d)shows the situation of adding d3 to join the tree.Fig.1(e)describes how the last destination node d2 joins the tree whereby the multicast tree Tmis eventually formed as shown in Fig.1(f).It is worth noting that the constraints are not aggregated in the proposed algorithm but are used to examine the feasibility of the obtained solution.We did not consider the case where the weight of the obtained solution violates the corresponding constraint.Investigating the relationship among constraints and their weight con figuration are interesting topics for our future work.

C.Analysis

Theorem 1:The time complexity of FAMOUS isO(km+nlogn).

Fig.1.An illustrative example of FAMOUS execution.

Proof:In Line 1,calling EWA takesO(Km)time to calculate the aggregated weight for each edge.Line 2 initializes the adjacent information for each node that needsO(n)time.The for-loop from Line 4 to Line 10 consumesO(n)for marking the neighbors of the source node.In the while-loop,selecting an appropriate node from the rest of node set can be done withinO(nlogn)time,while the if-statement costs constant time.The relaxation operation from Line 16 to Line 23 requiresO(m)time.That is to say,the entire while-loop takesO(m+nlogn).Therefore,the time complexity of FAMOUS isO(Km+nlogn).

Theorem 1 indicates that FAMOUS has much lower time complexity compared with a representative algorithm Heur-MOMT in[11].This is due to the facts that the employed EWA is able to simplify the problem efficiently by aggregating the weights and that FAMOUS does not need to check the feasibility of the tree,which lead to a significant reduction in time complexity.For the space complexity of FAMOUS,it is not so hard that we leave it to readers.Next,we analyze the asymptotical approximation performance of FAMOUS.

Theorem 2:FAMOUS finds aρ-approximation for MOMT,whereρ=min1≤k≤K{1/αk}.

Proof:For the optimal multicast treeTopt,we have

where 1≤k≤K,that is

AssumeWm=min1≤k≤K{Wk},then∀k∈[1,K],the above inequality can be rewritten as

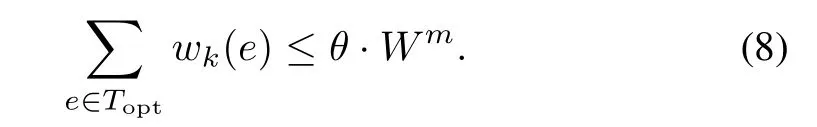
By multiplingαkon each side and summing the above equation overKweights we can get

that is

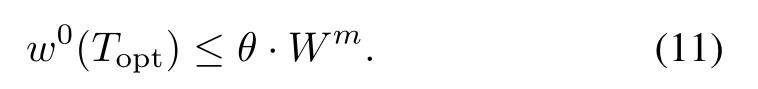
Also,since the SPTTmis computed via the weightw0,we havew0(Tm)≤w0(Topt).Therefore,

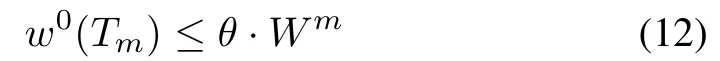
this implies

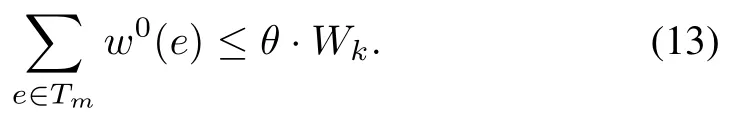
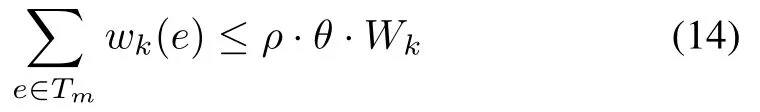
i.e.,

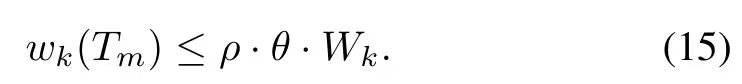
Theorem 2 implies that the approximation ratio of FAMOUS depends on the coefficient of weight aggregation.From an approximation perspective,the quality of solution should be worse than that of HeurMOMT[11]since there is a trade-off between “optimality”and “simplicity”.However,the approximation ratio of FAMOUS is possibly smaller than that of HeurMOMT as they are decided by different types of parameters.In the next section we shall examine the FAMOUS performance through extensive experiments.

IV.PERFORMANCE EVALUATION

In this section,we evaluate the FAMOUS algorithm by comparing its performance against that of a representative multicast routing algorithm HeurMOMT[11]via extensive experiments.We select HeurMOMT as the baseline for comparison because FAMOUS and HeurMOMT fall in the same category–approximation-based algorithms;thus are comparable in terms of both effectiveness and efficiency.There are exact algorithms for solving MOMT problem by searching the Pareto set,which is typically time-consuming or even impossible as it is readily proved to be NP-complete.Therefore,such algorithms are not applicable to the inter-cloud networking scenario,which requires faster and more efficient multicast algorithms.Our algorithm is developed with an approximation perspective to address this challenge.To the best of our knowledge,the most recent approximation algorithms dedicated to MOMT are HeurMOMT and fully polynomial time approximation scheme(FPTAS)published in[11].The HeurMOMT algorithm runs faster than the FPTAS algorithm and is catered for intercloud networking very well.Therefore,the performance of the proposed algorithm is compared against that of HeurMOMT.Our comparison is conducted in two aspects:the speed and the accuracy of the algorithm.

A.Experiment Setup

We adopt the same experiment settings from[11]in order to compare the performance unbiasedly.A set of random network topologies generated by Waxman[16]model is adopted here:the nodes are randomly placed in a one-by-one square,and the probability of creating a link between nodeuand nodevisα·e-d(u,v)/βL,whered(u,v)is the distance betweenuandv,andLis the maximum distance between any two nodes.αandβare set to 0.6 and 0.4 respectively to guarantee that each generated topology is a connected graph.The network size used in the experiment ranges from 100 nodes to 500 nodes,and the number of destinations is set to 5 and 10.

Regarding QoS parameters,we setKto 2,3,and 4,i.e.,each edge is associated with two or three or four weights,which are uniformly generated in a given range[1,100].The constraints are all set to 1000.In our experiments,the average results are reported by running each test instance one hundred times independently,and all the experiments are run on an IBM P4 2.4GHz PC with 4GB memory.

Note that the topologies as well as QoS parameters used in the experiments are generated randomly,which are representative enough to test the speed and accuracy of the proposed algorithm.Essentially in a practical inter-cloud environment,multicast routing usually happens in regular topologies as data centers are interconnected by specific networks,which are much simpler than the randomly generated topologies.

In the proposed algorithm the constraints are not aggregated but are used to examine the feasibility of the obtained solution.We did not consider the case where the weight of the obtained solution violates the corresponding constraint.The constraint values used in the experiments were set to be large enough so that generated solution always satisfies the constraints.

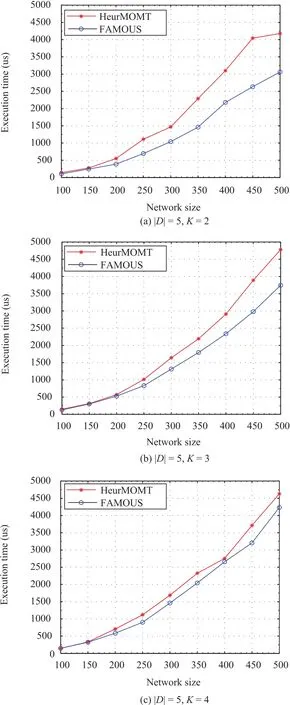
Fig.2. Execution time comparison.

B.Performance Metric

The performance metrics used in the rest of this section for evaluating FAMOUS and HeurMOMT are de fined as follows.

Definition 4(Execution Time):It indicates the average running time of an algorithm by its one hundred independent runs.This metric is used for evaluating time cost performance of an algorithm,i.e.,speed.

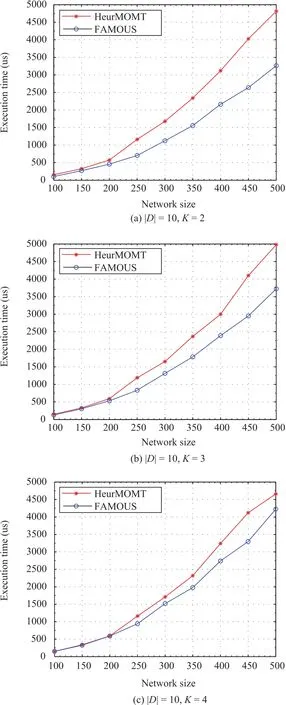
Fig.3. Execution time comparison.

Fig.4. Average weights comparison.

Definition 5(Average Weight):It denotes an aggregated weight of a tree returned by the algorithm,that is,for a treeTreturned by an algorithm

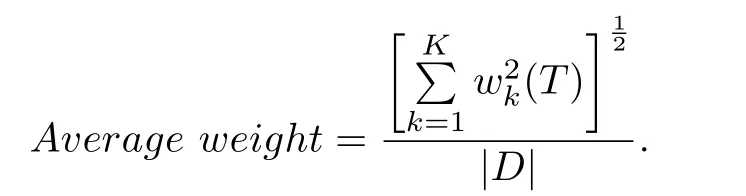
This metric reflects the quality of solution,i.e.,the accuracy of the algorithm.

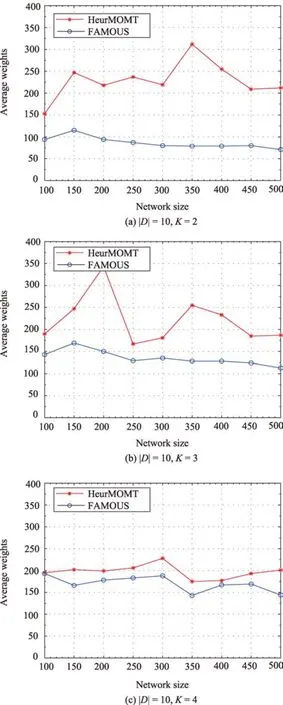
Fig.5.Average weights comparison.

C.Results

Figs.2 and 3 show the execution time of HeurMOMT and FAMOUS with different network sizes when|D|=5,10,K=2,3,4,respectively.It is obvious that the execution time of FAMOUS is lower than that of HeurMOMT,i.e.,FAMOUS is more time-efficient.On the other hand,Figs.4 and 5 plotthe comparison results regarding the average weights of Heur-MOMT and FAMOUS.The results demonstrate that the average weights of FAMOUS is lower than that of HeurMOMT,which means that FAMOUS is able to find a better solution than HeurMOMT.

TABLE IIRETURNED WEIGHTS COMPARISON WHEN|D|=5

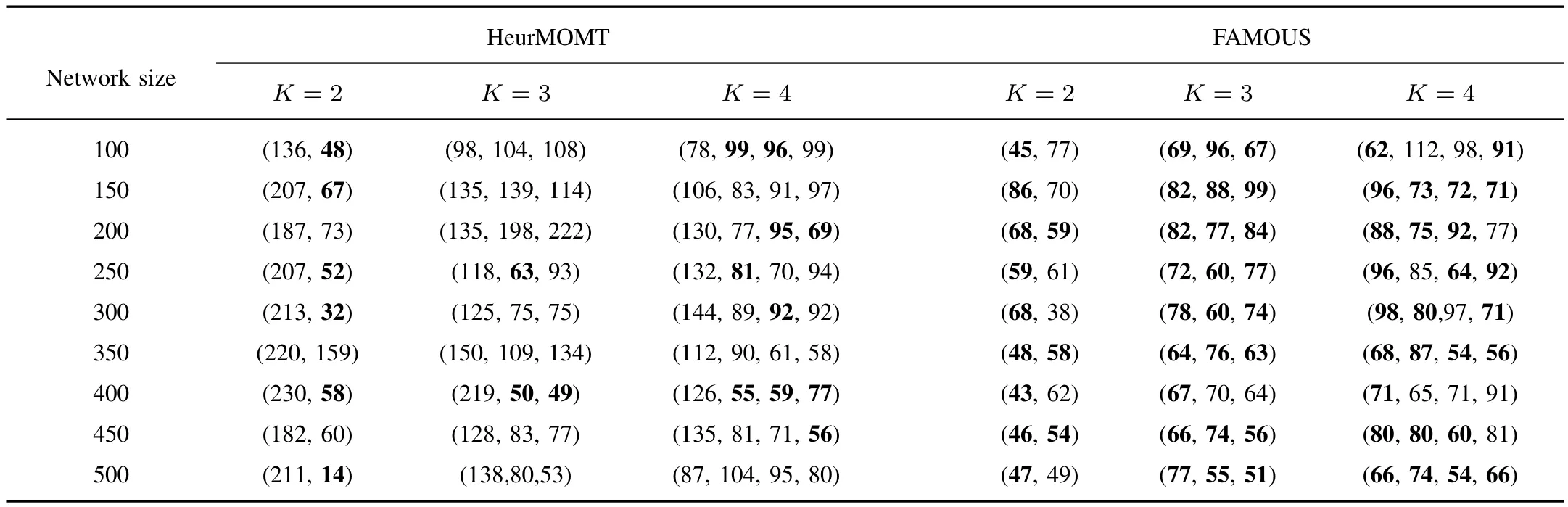
TABLE IIIRETURNED WEIGHTS COMPARISON WHEN|D|=10

In order to further evaluate the quality of FAMOUS solutions,we present the individual weight comparisons for two algorithms in Tables II and III.To distinguish the better result,the boldface is exploited to highlight the smaller weight.We can see from these tables that although FAMOUS is not able to excel HeurMOMT in every aspect,FAMOUS generates a more preferable tree than what HeurMOMT does in most cases.This observation matches our previous theoretical analysis.Therefore,we claim,on the basis of the above results,that FAMOUS is superior to HeurMOMT.

V.CONCLUSION

To address the multicast requirement of inter-cloud federation in the complex inter-cloud networking system,in this paper we have proposed a fast multi-constrained multicast routing algorithm withK≥2 constraints.The proposed algorithm applies the entropy technique to aggregate multiple constraints into a comprehensive metric,dramatically reduces the complexity of the multi-constrained multicast routing problem,and enables the application of the shortest path tree algorithm to solve the problem.We have presented theoretical analysis on the complexity and approximation of the proposed algorithm and have conducted extensive simulations to evaluate the performance of the algorithm.Both analytical and experimental results have demonstrated that the proposed algorithm is more efficient and superior to a representative multi-constrained multicast routing algorithm in the literature in terms of both speed and accuracy.

As future works,we plan to implement our algorithm in a practical inter-cloud environment and collect the real data trace to further evaluate the performance of the proposed algorithm.Also,the relationship among constraints and their weight con figurations are interesting topics that are worth to be investigated.

[1]B.Wang and J.C.Hou,“Multicast routing and its QoS extension:problems,algorithms,and protocols,”IEEE Netw.,vol.14,no.1,pp.22-36,Jan.-Feb.2000.

[2]M.R.Garey and D.S.Johnson,Computers and Intractability:A Guide to the Theory of NP-Completeness.San Francisco,CA:W.H.Freeman&Co Ltd,1979.

[3]H.Takahashi and A.Matsuyama,“An approximate solution for the Steiner problem in graphs,”Math.Japonica,vol.24,no.6,pp.573-577,Nov.1980.

[4]A.Z.Zelikovsky,“An 11/6-approximation algorithm for the network Steiner problem,”Algorithmica,vol.9,no.5,pp.463-470,May1993.

[5]G.Robins and A.Zelikovsky,“Improved Steiner tree approximation in graphs,”inProc.11th Annu.ACM-SIAM Symp.Discrete Algorithms,San Francisco,California,USA,2000,pp.770-779.

[6]K.Bharath-Kumar and J.M.Jaffe,“Routing to multiple destinations in computer networks,”IEEE Trans.Commun.,vol.31,no.3,pp.343-351,Mar.1983.

[7]S.Khuller,B.Raghavachari,and N.Young,“Balancing minimum spanning and shortest path trees,”inProc.4th Annu.ACM/SIAM Symp.Discrete Algorithms,Austin,Texas,USA,1993,pp.243-250.

[8]M.Parsa,Q.Zhu,and J.J.Garcia-Luna-Aceves,“An iterative algorithm for delay-constrained minimum-cost multicasting,”IEEE/ACM Trans.Netw.,vol.6,no.4,pp.461-474,Aug.1998.

[9]G.L.Xue,“Minimum-cost QoS multicast and unicast routing in communication networks,”IEEE Trans.Commun.,vol.51,no.5,pp.817-824,May2003.

[10]F.K.Hwang and D.S.Richards, “Steiner tree problems,”Networks,vol.22,no.1,pp.55-89,Jan.1992.

[11]J.Huang,Y.Tanaka,and Y.Ma,“On approximating a multicast routing tree with multiple quality-of-service constraints,”IEICE Trans.Commun.,vol.E95.B,no.6,pp.2005-2012,Jun.2012.

[12]Z.Wang and J.Crowcroft,“Quality-of-service routing for supporting multimedia applications,”IEEE J.Sel.Areas Commun.,vol.14,no.7,pp.1228-1234,Sep.1996.

[13]A.Ishizaka and P.Nemery,Multi-Criteria Decision Analysis:Methods and Software.New York:Wiley,2013.

[14]J.Huang,C.Q.Xu,Q.Duan,Y.Ma,and G.M.Muntean,“Novel endto-end quality of service provisioning algorithms for multimedia services in virtualization-based future internet,”IEEE Trans.Broadcast.,vol.58,no.4,pp.569-579,Dec.2012.

[15]J.Huang and Y.Tanaka,“A deployable E2E quality-of-service routing algorithm,”inProc.IEICE Gen.Conf.2011,Tokyo,Japan,No.BS-4-8,2011,pp.S-23-S-24.

[16]B.M.Waxman,“Routing of multipoint connections,”IEEE J.Sel.Areas Commun.,vol.6,no.9,pp.1617-1622,Dec.1988.