弹性边界径向功能梯度压电环板面内振动

胡统号， 沈纪苹， 姚林泉

(苏州大学 城市轨道交通学院， 江苏 苏州 215131)

板的振动分为面外振动(或横向振动)和面内振动，许多学者从不同角度应用不同方法对板的面外振动做了大量研究，而对面内振动的研究较少。近年来，随着板结构高频振动在工程中的应用，如盘式刹车片、驱动器硬盘和轨道车辆轮对等结构在运行中产生噪声的消除与振动的控制，故板结构面内振动的研究受到了更多的关注。面内振动作为板结构振动中的高频成分，不仅在能量传播中起主导作用，而且影响着低频振动[1]，因此对板结构的面内振动特性的研究具有重要意义。

Ambatid等[2]利用薄板和薄壁环中波的传动方程，求解了薄板和薄壁环面内自由振动频率，并指出轴对称薄板和薄壁环的面内振动包含面内纯剪切振动和面内纯径向振动，而非轴对称薄板和薄壁环的面内振动是纯剪切振动和纯径向振动的组合。Irie等[3]利用状态空间法获得各向同性圆环板在四种边界条件下的面内自由振动频率的解析解，讨论了环板内外径比对频率的影响。陈伟球等[4-5]利用状态空间法分别求解了横观各向同性功能梯度矩形板和功能梯度压电矩形板的自由振动问题，文中根据边界将面内振动和面外振动分开，给出了各自求解频率的特征方程。Zhong等[6]发展了该方法，将其用于四边简支的功能梯度压电矩形板的自由振动和受迫振动问题。Farag等[7]利用Bessel函数和三角函数给出了外边固定各向同性圆板的解析解，并给出了轴对称和非轴对称状态下圆板的振型图。Park[8]利用Hamilton原理，获得了四周固定的非轴对称各向同性圆板的面内振动耦合微分方程，并引入赫姆霍兹分解，将耦合的振动方程解耦，从而获得了该问题的解析解。Bashmal等[9-10]基于二维平面应力假设，利用Rayleigh-Ritz法求得了经典边界(自由，固定)和点弹性支撑边界下各向同性环板面内自由振动的解析解。Hashemi等[11-12]基于一阶剪切理论，求解了功能梯度圆环板和带有压电层的功能梯度圆环板的面内和面外耦合振动的解析解,并讨论了不同边界条件对频率的影响。Kim等[13]利用三角函数和Bessel函数给出了外边受弹性支撑的圆板面内自由振动的解析解，并通过讨论弹性支撑的刚度给出了外边自由和固定情况下圆板的振动频率特性和模态特性。蒲育等[14]基于线弹性体理论，利用微分求积法求解了各向同性材料薄圆环板自由振动数值解,讨论了四种边界条件下圆环板面内振动的频率特性。滕兆春等[15-18]在此基础上,将该方法分别应用于功能梯度薄圆环板的面内自由振动、温度影响下的功能梯度圆环板面内自由振动、厚度圆环板的面内自由振动和软芯夹层圆环板的面内自由振动。Wang等[19]基于平面应力假设，求得了简谐电压作用下的径向功能梯度压电圆环传感器共振与反共振频率的解析解。蒲育等将微分求积法应用于矩形板，求解了弹性约束边界下矩形板面内自由振动的无量纲频率特性。

本文在前人的基础上，考虑径向功能梯度压电环板的机电耦合作用，研究内外边弹性约束下径向FGPM环板的无量纲频率特性。讨论了内外径比、梯度指数、弹性边界的弹性刚度和压电效应对频率的影响；通过对径向FGPM环板模态特性进行研究，揭示了面内振动中径向振动和剪切振动的耦合特性，得到了具有普遍可遵循的规律，对工程实际应用具有指导意义。

1 基本方程

如图1所示，考虑径向功能梯度压电薄环板，上下表面不受载荷作用，内外半径分别为a和b，薄板厚度为l(远小于b)，在环板内外边界沿径向和周向均匀分布的弹簧，则该板处于平面应力状态。其弹性刚度分别为kni,kno,kτi和kτo，下标n代表沿法线方向，τ代表沿切向，i代表位于内径处，o代表位于外径处。

考虑材料为径向功能梯度压电材料，一般材料物性参数以幂函数或指数函数变化，假设材料径向物性参数按幂函数变化

(1)

式中：P为材料物性参数，包括弹性模量、压电常数、介电常数和密度;Pi和Po分别表示内径和外径处的物性参数;p代表功能梯度幂指数;r代表径向坐标。研究表明，泊松比的变化对于功能梯度板的力学性能影响较小[20-21]，可以忽略其变化，所以一般假设泊松比为常数，本文同样假设泊松比为常数。

(a)

(b)图1 弹性边界上径向功能梯度压电环板 Fig.1 Radial FGPM annular plate resting on elastic foundation

在柱坐标(r,θ,z)中，径向位移分量为ur=ur(r,θ,t)，周向位移分量为uθ=uθ(r,θ,t)，根据二维线弹体理论，几何方程为

(2)

式中：εrr,εθθ和γrθ分别表示径向正应变、周向正应变和切应变。

压电材料的本构方程为

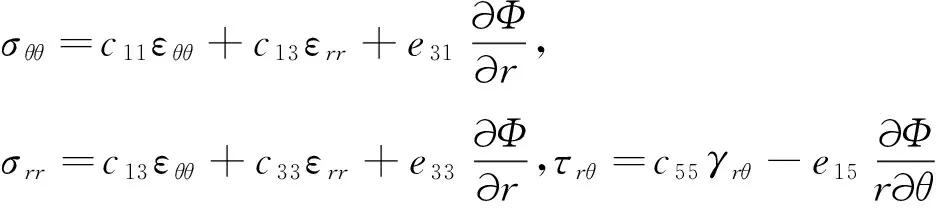
(3)

式中:σrr,σθθ和τrθ分别表示径向正应力、周向正应力和切应力;Drr和Dθθ分别为径向和周向电位移;Φ=Φ(r,θ,t)表示电势;cij表示弹性模量;eij表示压电常数;λii表示介电常数。

Maxwell电位移守恒方程

(4)

运动微分方程

(5)

式中:iir和iiθ表示对时间的二次导数，ρ为密度。

对于内外边弹性约束下的环板，其力学边界条件为

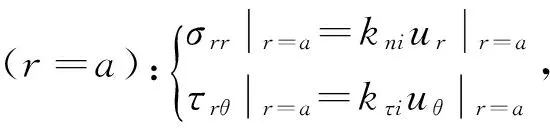
(6)

对于电场，考虑两种电学边界条件

电学开路：Φ|r=a=Φ|r=b=0 电学闭路：Drr|r=a=Drr|r=b=0

(7)

引入无量纲参数及变量

(8)

由式(2)和式(8)可得无量纲几何方程为

(9)

由式(3)和式(8)可得无量纲本构方程为

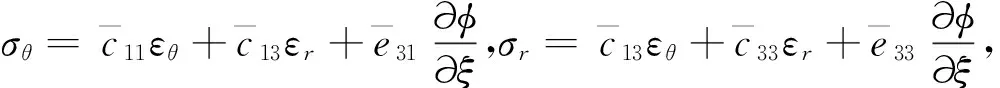
(10)

由式(4)和式(8)可得无量纲Maxwell电位移守恒方程为

(11)

由(5)式和(8)式可得无量纲运动微分方程为

(12)

由式(6)和式(8)可得无量纲力学边界条件为

(13)

由式(7)和式(8)可得无量纲电学边界条件为

电学开路：φ|ξ=η=φ|ξ=1=0 电学闭路：Dr|ξ=η=Dr|ξ=1=0

(14)

将式(9)和式(10)代入式(12)和式(11)，可得用位移及电势表示的平衡方程和Maxwell电位移守恒方程

(15)

系数中，□′表示变量对ξ的一阶导数。

根据参考文献[22],对于面内自由振动的环板，位移场可写成时间分量和位移分量分开的谐波形式，当位移假设成谐波形式时，相应的应变也是谐波形式，因此，由应变产生的电势也假设为谐波形式，具体表达如下

(16)

将式(16)代入式(15)，可得功能梯度环板面内自由振动振型的控制微分方程为

(17)

将式(9)和式(16)代入式(13)得用位移表示的力学边界条件为

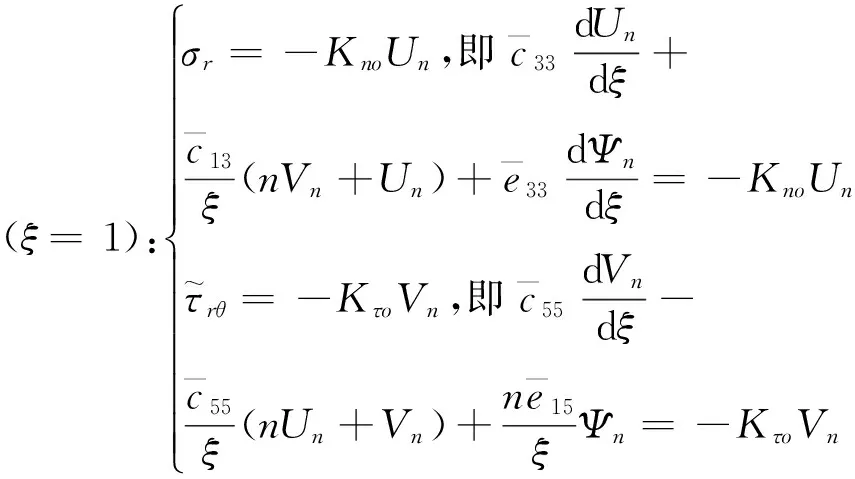
(18)

当Kni、Kno、Kτi和Kτo分别取不同的值时，可以得到不同的边界条件：

自由边界(F)：Kni=Kτi=0；

固定边界(C)：Kni=Kτi=∞；

特殊边界1(S1)：Kni=∞,Kτi=0；

特殊边界2(S2)：Kni=0,Kτi=∞。

将式(9)和式(16)代入式(14)得用位移表示的电学边界条件为

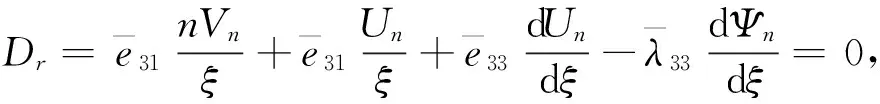
(19)

可以看出，式(17)是变系数二阶耦合微分方程，直接求解是非常困难的，下面利用微分求积法(DQM)进行求解。

2 DQM离散化及特征值问题

微分求积法是将函数在求解区域内的每个点处的导数值用全部区域内若干个节点上的函数值的加权线性和来近似表示。因此，利用DQM可以将微分方程转变为用节点处函数值表示的一组代数方程。在使用该方法时，有以下三个问题要确定:

(1)节点的选取，根据参考文献[23]，FGPM环板在径向上节点划分采用如下公式

(20)

式中：N表示选取节点总数，η表示内外径比。

(2)权系数矩阵的确定，根据文献[24]，得到一阶导数权系数矩阵显示表达为

(21)

根据式(21)，二阶导数权系数可用一阶导数权系数求得

[Bij]=[Aij][Aij]=[Aij]2

(22)

根据式(20)～(22)，利用DQM对运动微分方程式(17)进行离散化，可得

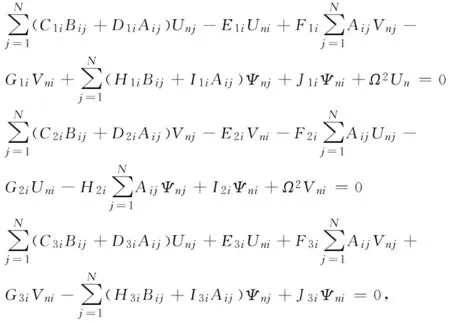
(23)

其中：

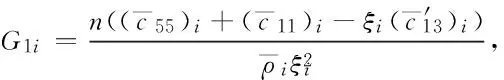
(3)边界条件的处理，二阶微分方程求解每个端点只需一个边界条件，引入边界条件时直接将边界条件节点坐标代入边界条件即可。因此，用DQM分别离散边界条件式(18)和式(19)，可得离散化的力学边界条件为

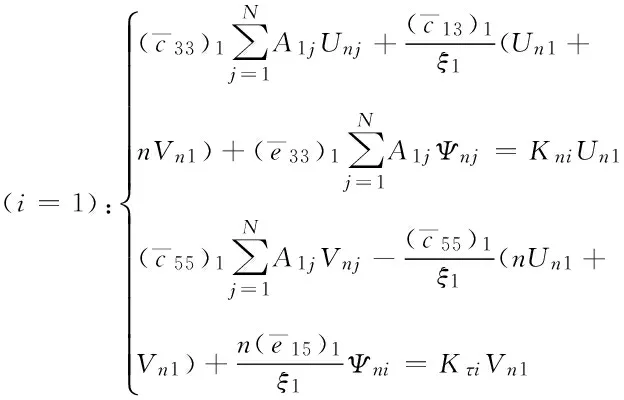
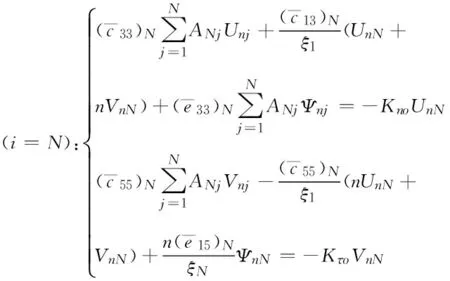
(24)

离散化的电学边界条件为

(25)

将微分方程式(23)与边界条件式(24)和式(25)对应联立便构成了不同边界条件下功能梯度环板面内振动的边值问题，该问题可用分块矩阵的形式表示

(26)

式中:Kbb和Kbd为由运动方程导出的刚度矩阵，Kdb和Kdd为由边界条件导出的刚度矩阵，M表示(3N-6)阶矩阵，0表示各阶零矩阵，具体表达如下

(27)

式中：I表示(2N-4)阶单位阵；0表示各阶零矩阵；qb和qd分别为环板内部和边界处的节点位移列向量，具体表示为

qb=[Un2,Un3,…,Un(N-1),Vn2,Vn3,…,Vn(N-1),Ψn2,Ψn3,…,Ψn(N-1)]T

qd=[Un1,UnN,Vn1,VnN,Ψn1,ΨnN]T

由式(26)消去qd，可得功能梯度环板面内自由振动的特征值方程为

(28)

3 算 例

3.2 非压电FGM环板的频率

对于径向功能梯度压电环板自由振动的文章未见报道，因此没有参考文献来验证本文获得结果的有效性。但是对于非压电功能梯度环板的面内自由振动已有报道[14]。因此。首先验证该方法对于非压电材料的面内自由振动特性求解的有效性。通过编写Matlab程序可获得方程(27)特征值问题的无量纲频率(以下简称频率)。算例中，节点数N=18，环向波数n取1和2，内外径比η取0.2，0.4，梯度幂指数p取1和5。表1给出了内边自由外边加紧(F-C)和内外边加紧(C-C)边界条件下前3阶频率Ω,并将得到的结果与文献[14]的结果对比,本文和文献[14]采用相同的DQM数值方法和材料，但是文献[14]假设泊松比是功能梯度变化的，而表1给出的本文数据假设泊松比为常数μ=(μm+μc)/2=0.294 4，其中μm和μc参考文献[14]。从表1数据可以看出，泊松比对环板面内自由振动频率影响很小，可以忽略不计，这与文献[20-21]的结论相同。

表1 FG环板面内自由振动无量纲频率Tab.1 FGM annular plate dimensionless frequency ofin-plane free vibration

3.2 径向FGPM环板面内自由振动

3.2.1 径向FGPM环板面内自由振动频率特性分析

对于径向FGPM环板的面内自由振动，在进行数值计算时径向节点数N=18，讨论F-C,C-F,C-C,S1-S2四种边界条件下径向FGPM环板的频率特性，讨论内外径比η，功能梯度幂指数p、弹性约束的刚度系数以及压电效应对频率的影响。内外径处的压电材料分别采用锆钛酸铅PZT-4和无铅压电陶瓷Ba2NaNb5O5，表2给出了这两种压电材料的一些常数。

表2 压电材料常数Tab.2 material constant of some piezoelectric materials

(1)梯度幂指数p对频率Ω的影响

图2给出了FGPM环板在F-C,C-F,C-C三种边界条件下，前5阶面内自由振动频率Ω随梯度幂指数p的变化曲线，其中径向节点数N=18,内外径比η=0.4，周向波数n=1，梯度幂指数p取值范围为[0,100]。从图中可以看出，前5阶频率Ω随p的增大而减小，最后趋于一个稳定值，这是因为当η一定时，p越大，FGPM环板的体积分数越小。因此，当p趋于无穷大时，PZT-4体积分数趋于零，根据式(1)，P(r)=Po为常数，得到的频率为均匀压电材料(Ba2NaNb5O5)的频率。

(2)弹性边界的弹性刚度对频率Ω的影响

图3给出了当n=1，p=1，η=0.4时，假设同一边界上切向刚度等于法向刚度，内边分别自由和固定情况下，外边弹簧刚度系数kno和kτo与频率之间的关系曲线，从曲线可以出，随着外边弹簧刚度系数kno和kτo的增大，前五阶频率逐渐增大，最后趋于一个稳定值。具体而言，对于内边自由时，该稳定值为F-C边界条件下对应的前5阶频率；而对于内边固定时，该稳定值为C-C边界条件下对应的前5阶频率。

(a)F-C (b)C-F (c)C-C图2 F-C,C-F,C-C边界条件下梯度幂指数p与无量纲频率Ω之间的关系曲线(n=1,η=0.4) Fig.2 Graded index p vs dimensionless natural frequencies Ω with F-F,F-C,C-F,C-C boundary conditions(n=1,η=0.4)

(a)内边自由 (b)内边夹紧图3 弹簧刚度系数Kno和Kτo与前五阶无量纲频率Ω之间的关系曲线(n=1，p=1，η=0.4) Fig.3 Spring stiffness coefficient Kno and Kτo vs dimensionless natural frequencies Ω(n=1，p=1，η=0.4)

图4给出了当n=1，p=1，η=0.4时，一种特殊边界条件S1-S2的刚度系数与基频Ω1的关系曲线。其中Kni=Kτo=∞，而Kτi和Kno在区间[0,104]之间变化，且采用对数坐标。从图4(a)可知，当切向刚度Kτi取定值时，当Kno∈[0.1,100]时，基频Ω1随着法向刚度Kno的增大而增大，增长趋势较为明显；而当Kno>100时，基频Ω1随着法向刚度Kno的增长趋势趋于平缓，当法向刚度系数Kno增大到一定值时，基频基本保持不变Ω1。从图4(b)可知，当法向刚度Kno取定值时，基频Ω1随切向刚度Kτi的增大具有类似图(a)的变化趋势。事实上，图3和图4表明，当弹簧刚度系数增大到一定值时，弹性过渡到“刚性”状态，弹性刚度对基频的影响就非常小了，弹性刚度越大，频率越高。当Kτi=Kno=1 000时，Ω1=3.177，这与C-C边界条件下的计算结果(Ω1=3.179)非常吻合，此时S1-S2边界条件下的环板可视为内外固定C-C环板。通过对比图4(a)和(b)，可以看出法向刚度Kno比切向刚度Kτi对基频Ω1的影响更为显著。

(a)Kno与Ω1关系 (b)Kτi与Ω1关系图4 S1-S2边界条件下刚度系数Kno和Kτi与基频Ω1的关系曲线(n=1，p=1，η=0.4) Fig.4 Spring stiffness coefficient Kno and Kτi vs dimensionless fundamental frequencies Ω1(n=1，p=1，η=0.4)

(a)F-C (b)C-F (c)C-C图5 F-C,C-F,C-C边界条件下内外径比η与一阶无量纲频率Ω1之间的关系曲线(n=1) Fig.5 Radius ratios η vs the 1st dimensionless natural frequencies Ω1 with F-C,C-F,C-C boundary conditions(n=1)

(3)内外径比η对频率Ω的影响

图5给出了FGPM环板面内自由振动在F-C,C-F,C-C三种不同的边界条件下，一阶频率Ω1随内外径比η的变化曲线，其中径向节点数N=18，周向波数n=1，内外径比η取值范围为[0.2,0.8]。从图中可以看出：当p一定时,一阶频率Ω1随着内外径比η的增大而增大，当η一定时，一阶频率随着梯度幂指数p的增大而减小。

(4)压电效应对频率Ω的影响

假设表2中两种压电材料常数中的弹性模量保持不变，而各压电系数和介电系数变为零，从而得到两种非压电材料组成的径向功能梯度(FGM)环板。图6给出了F-C,C-F,C-C边界条件下，周向波数n=1，内外径比η=0.4时，材料的压电效应对频率的影响曲线，其中虚线和实线分别代表径向FGPM环板和径向FGM环板第一、三和五阶频率随梯度幂指数的变化曲线。

(a)F-C (b)C-F (c)C-C图6 F-C,C-F,C-C边界条件下压电效应与无量纲频率Ω之间的关系曲线(n=1,η=0.4) Fig.6 Radius ratios η vs the 1st dimensionless natural frequencies Ω with F-F,F-C,C-F,C-C boundary conditions(n=1, η=0.4)

从图6(a)～(c)可以看出：压电效应使各阶环板的面内自由振动频率有不同程度的增大，且对于高阶频率的影响相对显著。

3.2.2 径向FGPM环板面内自由振动模态特性分析

由蒲育等研究可知，面内自由振动分为面内径向振动和面内剪切振动，尤其在轴对称情况下面内径向振动和面内剪切振动是独立存在的，仅从频率数值上无法区分这两种振动成分，为了区分这两种频率，有必要对面内振动的模态特性进行研究。

图7 F-C边界条件下径向FGPM环板面内自由振动振型图(p=1，η=0.2，n=1～4) Fig.7 Mode shapes for in-plane free vibration of radial FGPM annular plate with F-C boundary condition (p=1，η=0.2，n=1～4)

图8 C-F边界条件下径向FGPM环板面内自由振动振型图(p=1，η=0.2，n=1～4) Fig.8 Mode shapes for in-plane free vibration of radial FGPM annular plate with C-F boundary condition (p=1，η=0.2，n=1～4)

图9 C-C边界条件下径向FGPM环板面内自由振动振型图(p=1，η=0.2，n=1～4) Fig.9 Mode shapes for in-plane free vibration of radial FGPM annular plate with C-C boundary condition (p=1，η=0.2，n=1～4)

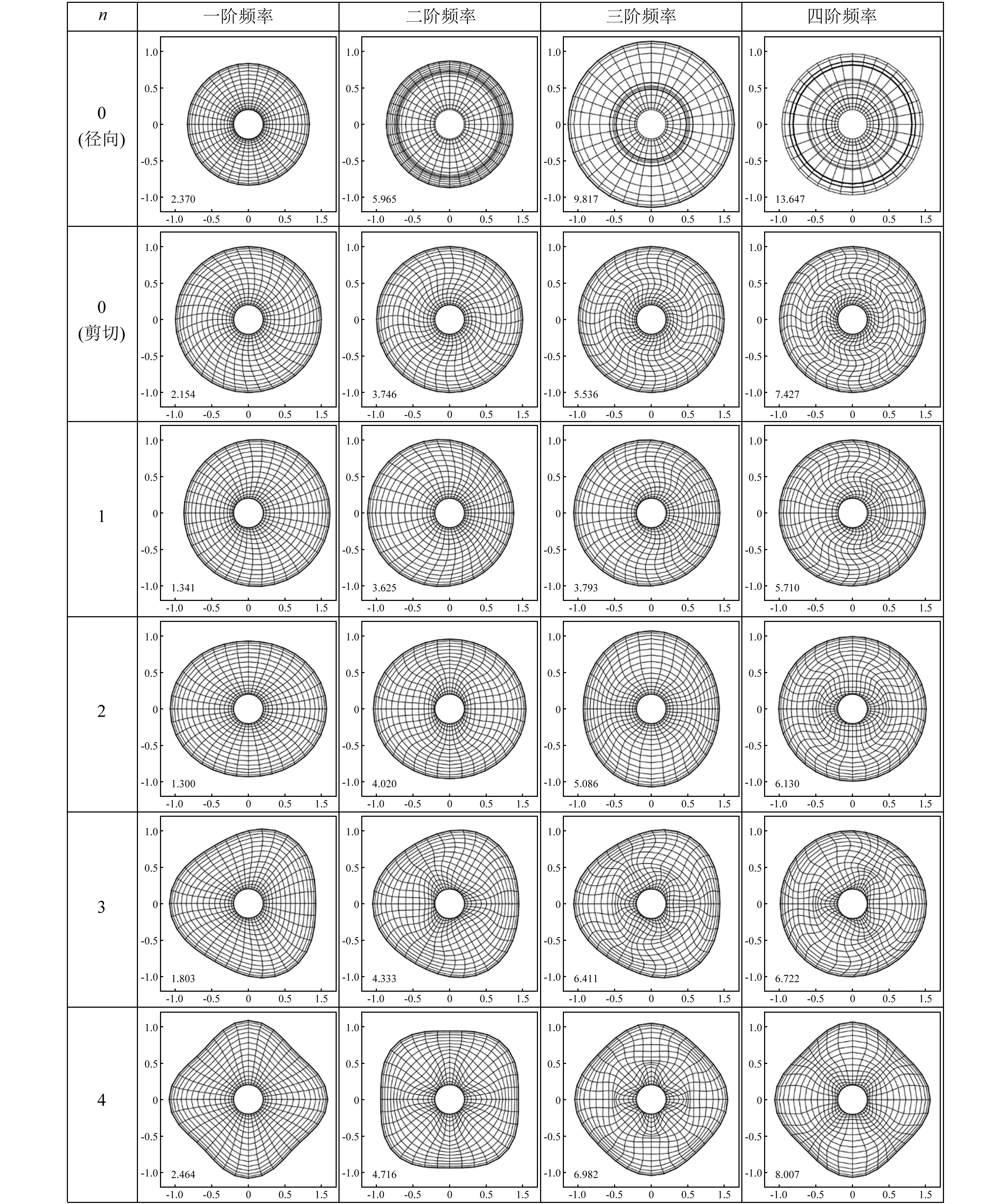
图10 S1-S2边界条件下径向FGPM环板面内自由振动振型图(p=1，η=0.2，n=1～4) Fig.10 Mode shapes for in-plane free vibration of radial FGPM annular plate with S1-S2 boundary condition (p=1，η=0.2，n=1～4)

图7～图9给出了三种经典边界条件(F-C,C-F,C-C)下，梯度幂指数p=1，内外径比η=0.2，环向波数n=0～4时，径向FGPM环板前四阶模态图，左下角数字是该模态对应的频率值。从图7～图9可以看出：其中当n=0时，FGPM环板处于轴对称状态，面内自由振动中的径向和剪切振动独立存在，仅发生径向振动称为纯径向模态，仅发生剪切振动称为纯剪切模态[12]；当n≥1时，面内自由振动中的径向振动和剪切振动耦合，即同时存在这两种振动成分，这种模态被称为混合模态[13]。

图10给出了S1-S2边界条件下，梯度幂指数p=1，内外径比η=0.2，环向波数n=0～4时，径向FGPM环板前四阶模态图。从图中可以看出：在内径处，仅存在切向位移，而无法向位移；相反在外径处，只存在径向位移，而无切向位移。这一特性与特殊边界S1(Kn=∞,Kτ=0)和特殊边界S2(Kn=0,Kτ=∞)的假设一致。同理，从图7～图9可以看出：对于自由边界，同时存在切向位移和法向位移；而对于固定边界，既无切向位移，也无法向位移。

4 结 论

基于二维线弹性体理论研究了径向FGPM环板的面内自由振动，得到FGPM环板面内自由振动的运动微分方程，用DQM求解得到了FGPM环板面内自由振动的频率。将材料退化为非压电材料时，本文得到的结果与已有的FGM环板面内自由振动结果相当吻合，验证了泊松比对FGM板的力学性能影响较小的结论；在径向节点数N=18时，所求结果就具有很高的精确度显示了DQM法的精确性和高效性。

文中考虑了弹性边界和两种电学边界条件组合情况下FGPM环板的面内自由振动特性。根据内外边弹簧的刚度系数取值的不同可以将环板分为自由(F)、固定(C)、特殊边界1(S1)和特殊边界2(S2)四种不同的边界形式。当有一边固定(F-C,C-F,C-C)时，前五阶频率表现出一定的规律性，对工程应用具有一定的参考价值。本文考虑两种情况下弹性边界的弹性刚度对频率的影响，一是假设切向刚度Kno和法向刚度Kτo相同时，当内边分别自由和固定时，FGPM环板面内振动频率随着外边弹簧弹性刚度Kno和Kτo的增大而增大，并最终趋于稳定值；另外讨论了特殊边界(S1-S2)下，基频Ω1随内边切向刚度Kτi和外边法向刚度Kno的变化规律，结果显示，弹性边界的弹性刚度越大，频率越大，当刚度大到一定值后，弹性边界过渡为刚性边界，基频趋于稳定值，根据该特性，工程中可以通过改变弹性边界的刚度获得所需频率。因此，本文的研究对工程应用提供参考依据。

通过对径向FGPM环板面内自由振动模态特性的分析，充分说明了在轴对称状态下，面内径向振动和面内剪切振动独立存在，并且区分了这两种模态成分，给出了相对应的频率值；而非轴对称状态下，面内径向振动和面内剪切振动耦合存在，这一规律对于进一步了解径向FGPM环板面内自由振动具体形式具有指导意义。

[ 1 ] 蒲育, 滕兆春, 赵海英. 四边弹性约束矩形板面内自由振动的DQM求解[J]. 振动与冲击, 2016, 35(12): 55-60.

PU Yu, TENG Zhaochun, ZHAO Haiying. In-plane free vibration analysis for rectangular plates with elastic restrained edges by Differential Quadrature Method[J]. Journal of Vibration and Shock, 2016, 35(12): 55-60.

[ 2 ] AMBATI G, BELL J F W, SHARP J C K. In-plane vibrations of annular rings[J]. Journal of Sound and Vibration, 1976, 47(3): 415-432.

[ 3 ] IRIE T, YAMADA G, MURAMOTO Y. Natural frequencies of in-plane vibration of annular plates[J]. Journal of Sound and Vibration, 1984, 97(1):171-175.

[ 4 ] 陈伟球, 叶贵如, 蔡金标, 等. 横观各向同性功能梯度材料矩形板的自由振动[J]. 振动工程学报, 2001, 14(3): 263-267.

CHEN Weiqiu, YE Guiru, CAI Jinbiao, et al. Free vibration of transversely isotropic FGM rectangular plates[J]. Journal of Vibration Engineering, 2001, 14(3): 263-267.

[ 5 ] CHEN W Q, DING H J. On free vibration of a functionally graded piezoelectric rectangular plate[J]. Acta Mechanica, 2002, 153(3/4): 207-216.

[ 6 ] ZHONG Z, YU T. Vibration of a simply supported functionally graded piezoelectric rectangular plate[J]. Smart Materials and Structures, 2006, 15(5): 1404-1412.

[ 7 ] FARAG N H, PAN J. Modal characteristics of in-plane vibration of circular plates clamped at the outer edge[J]. The Journal of the Acoustical Society of America, 2003, 113(4): 1935-1946.

[ 8 ] PARK C I. Frequency equation for the in-plane vibration of a clamped circular plate[J]. Journal of Sound and Vibration, 2008, 313(1): 325-333.

[ 9 ] BASHMAL S, BHAT R, RAKHEJA S. In-plane free vibration of circular annular disks[J]. Journal of Sound and Vibration, 2009, 322(1): 216-226.

[10] BASHMAL S, BHAT R, RAKHEJA S. In-plane free vibration analysis of an annular disk with point elastic support[J]. Shock and Vibration, 2011, 18(4): 627-640.

[11] HASHEMIS H, FADAEE M, ES’HAGHI M. A novel approach for in-plane/out-of-plane frequency analysis of functionally graded circular/annular plates[J]. International Journal of Mechanical Sciences, 2010, 52(8): 1025-1035.

[12] HASHEMI S H, KHORSHIDI K, ES’HAGHI M, et al. On the effects of coupling between in-plane and out-of-plane vibrating modes of smart functionally graded circular/annular plates[J]. Applied Mathematical Modelling, 2012, 36(3): 1132-1147.

[13] KIM C B, CHO H S, BEOM H G. Exact solutions of in-plane natural vibration of a circular plate with outer edge restrained elastically[J]. Journal of Sound and Vibration, 2012, 331(9): 2173-2189.

[14] 蒲育, 滕兆春, 房晓林. 圆环板面内自由振动的 DQM 求解[J]. 振动与冲击, 2013, 32(24): 152-156.

PU Yu, TENG Zhaochun, FANG Xiaolin. In-plane free vibration of circular annular plates with differential quadrature method[J].Journal of Vibration and Shock, 2013, 32(24): 152-156.

[15] 滕兆春, 蒲育, 房晓林. FGM圆环板面内自由振动的 DQM 求解[J]. 北京理工大学学报, 2014, 12: 1211-1216

TENG Zhaochun, PU Yu, FANG Xiaolin. In-plane free vibration analysis for FGM annular plates by Differential Quadrature Method[J].Transactions of Beijing Institute of Technology,2014, 12: 1211-1216

[16] 滕兆春, 蒲育. 温度影响下FGM圆环板的面内自由振动分析[J]. 振动与冲击, 2015, 34(9): 210-217.

TENG Zhaochun, PU Yu. In-plane free vibration of FGM annular plates considering temperature effect [J]. Journal of Vibration and Shock, 2015, 34(9): 210-217.

[17] 滕兆春, 余文卿, 蒲育. 变厚度圆环板的面内自由振动分析[J]. 兰州理工大学学报, 2015, 41(3): 168-172.

TENG Zhaochun, YU Wenqing, PU Yu. In-plane free vibration of circular annular plates with variable thickness [J]. Journal of Lanzhou University of Technology, 2015, 41(3): 168-172.

[18] 滕兆春, 潘茂华, 蒲育. 软芯夹层圆环板的面内自由振动分析[J]. 科学技术与工程, 2015 (12): 132-136.

TENG Zhaochun, PAN Maohua, PU Yu. In-plane free vibration analysis of Soft-core Sandwich AnnualrPlates[J]. Science Technology and Engineering, 2015 (12): 132-136.

[19] WANG H M, LUO D S. Exact analysis of radial vibration of functionally graded piezoelectric ring transducers resting on elastic foundation[J]. Applied Mathematical Modelling, 2016, 40(4): 2549-2559.

[20] CHI S H, CHUNG Y L. Mechanical behavior of functionally graded material plates under transverse load—Part I: Analysis[J]. International Journal of Solids and Structures, 2006, 43(13): 3657-3674.

[21] CHI S H, CHUNG Y L. Mechanical behavior of functionally graded material plates under transverse load—Part II: Numerical results[J]. International Journal of Solids and Structures, 2006, 43(13): 3675-3691.

[22] YAS M H, JODAEI A, IRANDOUST S, et al. Three-dimensional free vibration analysis of functionally graded piezoelectric annular plates on elastic foundations[J]. Meccanica, 2012, 47(6): 1401-1423.

[23] BERT C W, MALIK M. Differential quadrature method in computational mechanics: a reviews[J]. Applied Mechanics Reviews, 1996, 49(1): 1-28.

[24] 王永亮. 微分求积法和微分求积单元法—原理与应用[D]. 南京: 南京航空航天大学, 2001: 13-16.