兰州地铁下穿黄河砂卵石地层中盾构刀具破岩的数值计算

杨 成， 赖远明，， 王 旭， 高建强， 魏周斌

(1.兰州交通大学 土木工程学院，兰州 730070； 2. 中国科学院西北生态环境资源研究院，兰州 730000；3. 兰州市轨道交通有限公司，兰州 730015)

兰州地理位置独特，呈现东西狭长分布，兰州地铁的建设能有效解决交通拥堵问题[1-5]。在城市地铁的建设中，盾构施工技术具有工期短、自动化程度高、安全性好以及对周边环境影响小等优点[6]，在现今地铁的建设中应用最广泛。

盾构刀盘中刀具属于易损易消耗的部件，刀具的消耗量直接决定着施工工期和工程造价。盾构机在砂卵石地层中掘进，掘削负荷较大，刀盘及刀具的消耗非常严重。因此在卵石层中盾构掘进对刀位的设计尤为重要。

基于上述原因，本文以兰州地铁一号线下穿黄河为背景，对砂卵石地层盾构刀盘中刮刀和滚刀的切削原理分析，从兰州砂卵石地层独有的物理特性、盾构机中刀具的配制以及工作原理出发，提出砂卵石地层刀具切削机理[7]。初步提出合理的刀具配制原则，对不同刀具的掘进参数进行深入分析，建立数学模型，通过有限元计算得到合理的刀具分部规律，减少刀具的消耗，从而确保工程的安全与经济性。

1 刀具的模型建立

1.1 岩土本构方程和材料属性

本构选用线弹性模型和扩展的线性Drucker-Prager塑性模型模拟卵石材料的本构关系，因为该模型可以较好的模拟卵石在滚刀作用下的挤压和剪切破坏过程，同时应用包含单元失效功能的剪切失效准则模拟卵石碎屑的形成及剥离过程，从而实现盾构刀具对卵石地层切削过程的分析。Drucker-Prager塑性模型的屈服准则及塑性势面的表达式则为[8-10]：

F=t-ptanβ-d=0

(1)

G=t-ptanψ

(2)

t=q/2[1+1/k-(1-1/k)(r3/q)]

(3)

式中：t为偏应力；p为等效压应力；β为线性屈服面在应力空间上的倾斜角，与材料的摩擦角φ有关；ψ为剪胀角；q为Mises等效应力；k为三轴拉伸强度与三轴压缩强度的比值，体现中主应力对屈服面的影响(k=0.8时为曲线n，k=1.0时为曲线m)；r为偏应力第三不变量；d为屈服面在应力空间t轴上的截距，即材料的黏聚力，与输入的硬化参数有关，由单轴抗压强度定义，则为：

(4)

由单轴抗拉强度定义，则为：

(5)

由剪切强度定义，则为：

(6)

进行三维分析时，Drucker-Prager模型中参数β和k可由摩擦角φ来标定，有：

(7)

为了保证屈服面是凸面，要求0.778≤k≤1。

1.2 接触属性

模型中的摩擦接触有：刮刀前面与卵石切屑面、刮刀后面与工件座基。“刮刀-切屑”和“刮刀-工件座基”的接触摩擦均采用修正的库仑摩擦模型，接触区的摩擦分为黏着区与滑动区。黏着区靠近刀刃，滑动区是从粘着区外到“刮刀-切屑”或“刮刀-工件座基”分离点处的区域[11-12]。不同区域计算摩擦力如公式(8)所示：

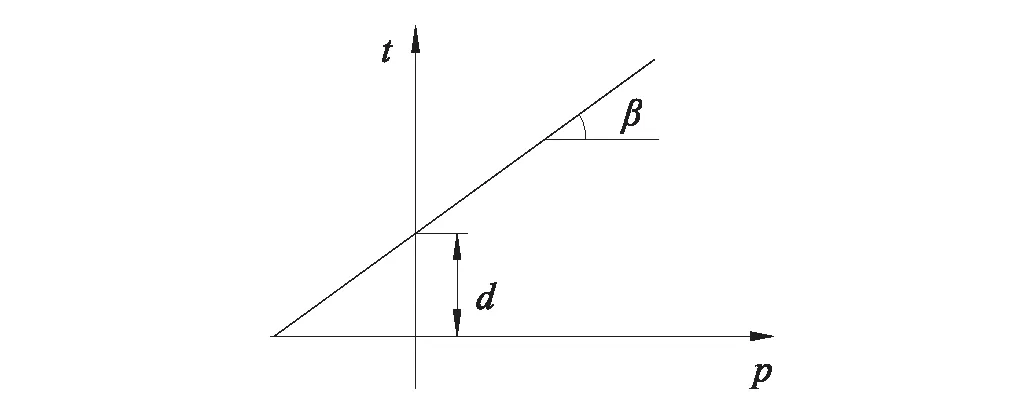
(a) p-t关系曲线

(b)D-P屈服面图1 扩展线性Drucker-Prager模型 Fig.1 Extended linear Drucker-Prager model

(8)

式中：μ为滑移区的摩擦因数；σ为正应力；τcrit为极限剪切应力。

“切屑-刀具-工件”的摩擦因数设置对破岩过程模型的切削力、切削温度、已切削表面残余应力和刀具磨损预测的准确性有重要的影响。

1.3 损伤-切削分离准则

材料从屈服到破坏是一个连续的过程，是材料损伤演变直至破坏的过程。该过程也可以描述成屈服应力软化和弹性模量退化的过程，材料在受到外界作用的初始阶段为弹塑性变形阶段，当材料达到强度极限后材料的塑性应变不断增大，在塑性变形阶段材料的塑形变形是不可逆的，在塑性变形达到一定阶段后材料达到了破坏损伤初始点，随着塑性变形的继续，材料内部会形成一些微观的缺陷并逐渐在材料内部扩散开来，最终塑性变形达到材料完全破坏点，此时材料完全被破坏掉，材料的应力为零。被破坏的材料单元不再参与后续的仿真步骤而被删除掉[13-14]。

图2 基于损伤演化的应力应变曲线 Fig.2 Stress-Strain curve based on damage evolution

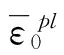
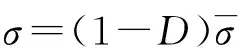
(9)

当D=1时，单元体的状态为不受力，该单元将失效，不参与后续的计算，从模型中删除，刀具继续与新单元发生接触，新单元受力发生弹塑性变形，再次发生破坏删除，以此类推进行计算[15-16]。

ABAQUS中的剪切分离准则是用以表征由损伤引起的剪切带形成过程，模型通过定义材料失效参数ωs来确定材料单元是否失效，ωs由下式确定：

(10)

(11)

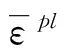
盾构刀具中刮刀与滚刀都采用以上本构关系进行仿真计算，盾构刀盘主要有滚刀和刮刀来协同工作，刮刀是将刀盘边缘地层的岩石刮向刀盘，进而让滚刀进行破碎，岩石粒径变小后，有分离系统将破碎后的岩石排出，对岩石而言刮刀先发挥刮刀的作用，后滚刀进行破岩工作。

2 刮刀的有限元分析

2.1 刮刀破岩模型建立

据现场实测数据显示，盾构下穿卵石层段主要以花岗岩、石英岩为主。本文计算分析中假定卵石层是均匀的各向同性材料。为了提高计算精度和效率，模型尺寸为50 cm×80 cm×20 cm。刮刀尺寸按照兰州地铁盾构实际尺寸建模，刀宽25 cm，刃角20.38°，建模中简化为20°。卵石层的相关参数见表1所示。

表1 砂卵石层材料参数Tab.1 Sand and gravel layer material parameters

本文将对刮刀的破岩效果进行分析。刮刀破岩机理研究中，均将刮刀定义为刚性体，不考虑其磨损的影响，此种处理方式便于有限元程序的收敛，提高计算效率。因此本模型在分析过程中，将刮刀认为是刚性体，卵石层认为弹塑性体，重点分析其在刮刀切削破岩过程中的破岩效果。同时为了研究刮刀在不同刀间距情况下的破岩效果及其影响规律，现建立单刃滚刀破岩有限元模型及一组不同刮刀间距下的双单刃滚刀破岩有限元模型，此处仅以刮刀间距S=120 mm为例列出，如图3所示。

图3 刮刀破岩有限元模型 Fig.3 Finite element model of blade breaking rock

2.2 刮刀计算结果分析

为研究影响刀具破岩及磨损的因素，现就刀具在不同切削速度、切削深度、切削角度、刀间距下的破岩效果进行分析，计算工况如表3所示。同时为了节省运算时间，本模型的运行时间设为0.5 s。

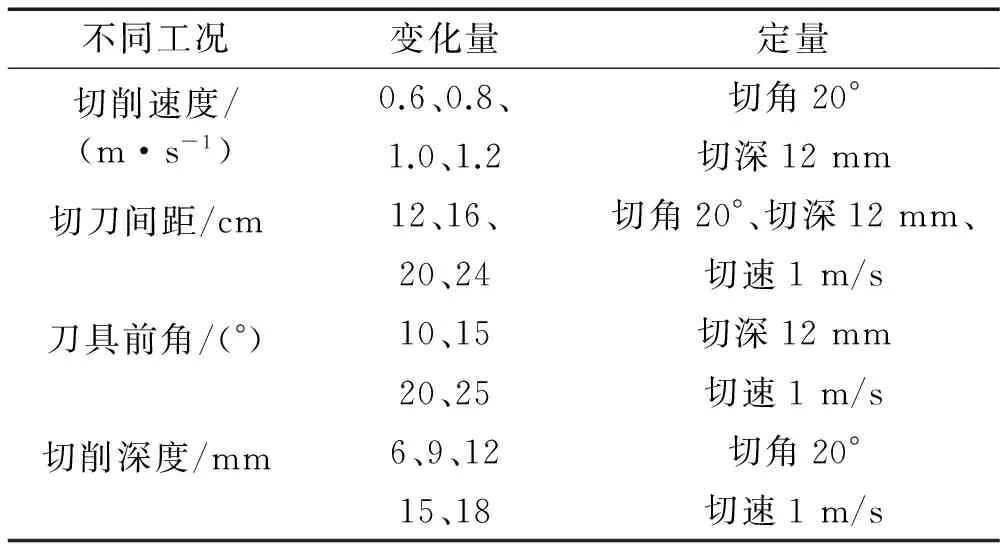
表2 刮刀破岩工况Tab.2 Scraper rock breaking conditions

2.2.1 不同切削速度

在研究切削速度对刮刀与土体接触力的影响时，保持刀具的其它相关掘进参数不变，设定切削角度为20°，切削深度为12 mm，仅改变刀具的切削速度，分别使刀具以0.6 m/s、0.8 m/s、1.0 m/s、1.2 m/s的速度模拟切削，计算结果如图4所示。

从图4中的刀具切削速度与卵石的等效应力关系可以得出，随着切削速度的不断增大，刀具的水平切削力变化不大，说明刀具切削速度的改变不对水平切削力产生影响。分析其原因为：盾构机推进过程中，刀具随着盾构刀盘的转动不断切削掌子面上的土体，属于低速切削。迄今为止，很少有讨论低速切削岩土材料时，速度对切削力影响规律的研究。一些研究人员描述：高速切削过程中，切削产生的热量引起被切削材料内摩擦角的变化，导致材料的应变率发生改变，在宏观上表现为被切削材料对刀具阻力的变化[17]。但对于低速切削而言，仅产生极小的切削热量，对被切削材料的影响可以忽略，因此刀具切削速度对切削阻力的影响不大，可以不考虑切削速度的影响。

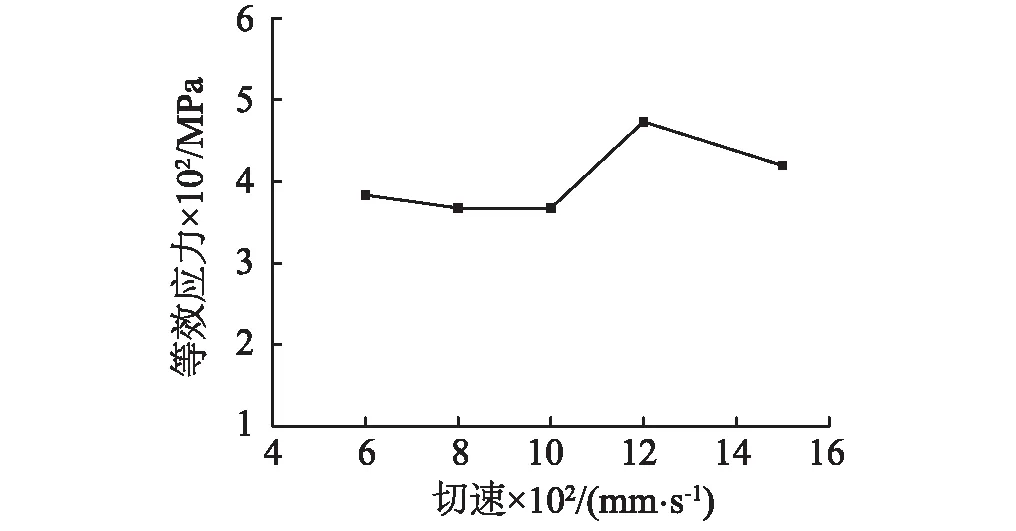
图4 刀具切速与卵石等效应力关系图 Fig.4 The relationship between cutting speed and pebble equivalent stress

2.2.2 不同刮刀间距

以建立的刮刀有限元模型为基础，设定切削角度为20°，切削深度为12 mm，切削速度为1 m/s。以刀具间隔分别为12 cm、16 cm、20 cm、24 cm的情况为例，对砂卵石层进行切削。

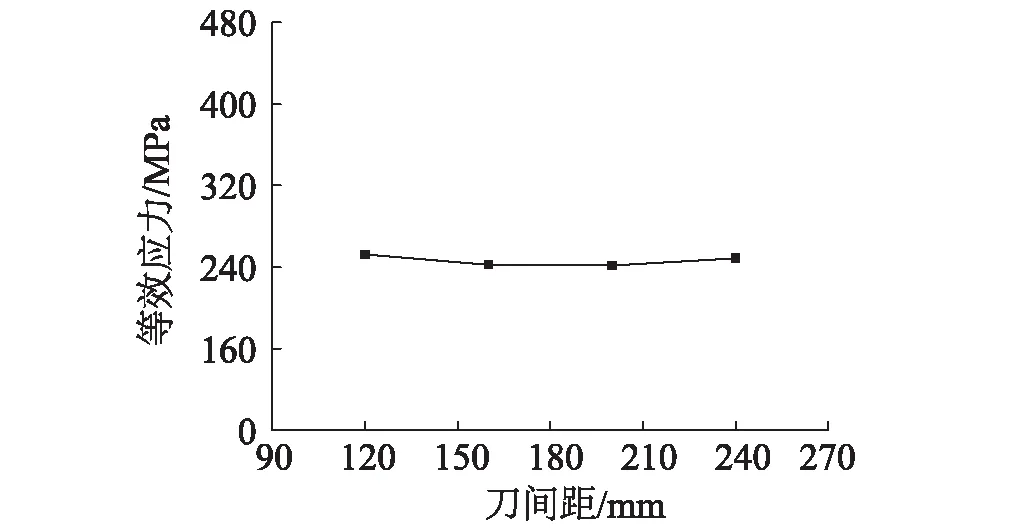
图5 刀间距与卵石等效应力关系图 Fig.5 Relationship between knife spacing and pebble equivalent stress

从图5中的刀间距与卵石等效应力关系可以得出，单把滚刀与多把滚刀的切削效果没有区别。

2.2.3 不同刀具前角

以建立的刮刀有限元模型为基础，实际施工中的刮刀的切削角度为20.37°。设定切削深度为12 mm，切削速度为1 m/s。以刀具切削角度分别为10°、15°、20°、25°的情况为例，对砂卵石层进行切削计算。

从图6中的刀具切角与卵石等效应力关系可以得出，刀具切削过程中，随刀具前角的增大，卵石的等效应力呈先缓慢增大，且在切角为20°时，发生突增。综合而言，兰州地铁穿黄泥水盾构机刀盘上实际工程上的刮刀切角为20.38°，具备良好的切削破岩效果。

图6 刀具切角与卵石等效应力关系图 Fig.6 The relationship between cutting angle and pebble equivalent stress

2.2.4 不同切削深度

以建立的刮刀有限元模型为基础，设定切削角度为20°，切削速度为1 m/s。以刀具切削深度分别为6 mm、9 mm、12 mm、15 mm、18 mm的情况为例，对砂卵石层进行切削计算。

图7 刀具切深与卵石等效应力关系图 Fig.7 The relationship between cutting depth and pebble equivalent stress

从图7中的刀具切深与卵石等效应力关系可以得出，随着切深的不断增加，刀具的水平切削力都不断增加，且增加幅度较明显，砂卵石土中尤为明显。这是由于刀具与土层接触面积增大，前刀面上摩擦阻力与粘聚力也随之增大，引发了刀具水平切削力的大幅增加，而砂卵石土中黏聚力增大更明显，摩擦阻力也增大的教多，因此在切削砂卵石土时切深对刀具切削力的影响更显著。所以实际施工中应控制切削深度，防止出现刀具受力过大，引起功率消耗大幅增加，从而使刀盘输出功率不能满足需要而引发堵转现象。

3 滚刀的仿真分析

3.1 单刃滚刀破岩有限元模型建立

滚刀采用17in的盘形滚刀，滚刀直径为432 mm，滚刀由刀圈及刀体组成如图8所示，刀圈为硬质合金。

分别对单刃滚刀破岩机理和不同滚刀间距下的破岩效果进行分析。目前滚刀破岩机理研究中，均将滚刀定义为刚性体，不考虑其磨损的影响，此种处理方式便于有限元程序的收敛，提高计算效率。因此本模型在分析过程中，刀圈为刚性体，卵石层为弹塑性体，重点分析其在滚刀滚压破岩过程中的破岩效果。同时为了研究滚刀在不同刀间距情况下的破岩效果及其影响规律，现建立单刃滚刀破岩有限元模型如图9所示，不同滚刀间距下的双刃滚刀破岩有限元模型如图10所示，此处仅以滚刀间距S=8 cm为例。滚刀破岩工况见表3所示。

图8 17in盘型滚刀有限元模型 Fig.8 17in Plate type hob finite element model

图9 单把滚刀有限元模型 Fig.9 Single-shot hob finite element model

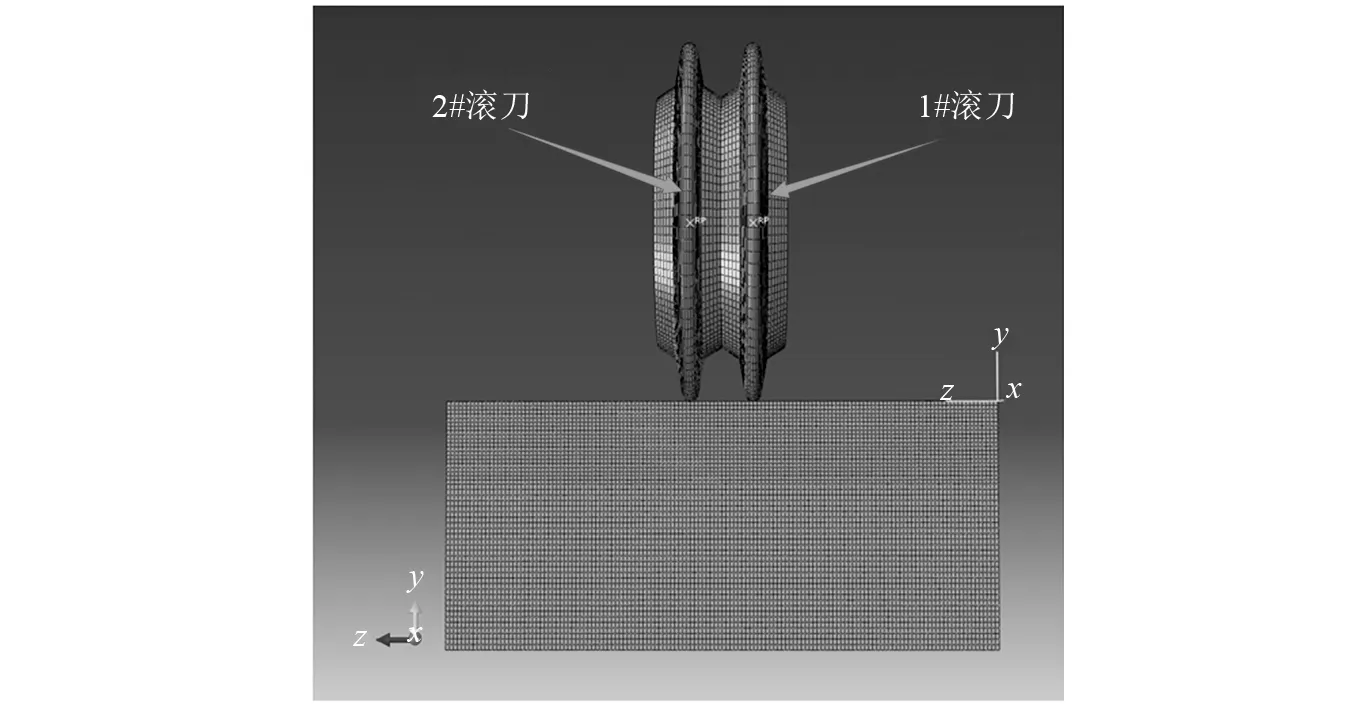
图10 双刃滚刀有限元模型(S=8 cm) Fig.10 Double-blade hob finite element model (S=8 cm)

工况变化量/cm不同滚刀间距8、12、16、20、25、30、36

3.2 滚刀计算结果分析

滚刀的切削可以分为两个分析步进行，即初始顶进阶段，该阶段盾构机刀盘由空转状态进入滚刀贯入卵石层的状态；以及刀盘掘进阶段，该阶段盾构机开始进入转动掘进状态，滚刀随刀盘的转动发生公转，滚刀与卵石层之间的摩擦力产生自转[18]。考虑到模型计算耗时过长，本计算模型设定初始顶进阶段为0.01 s，刀盘掘进阶段运算0.1 s，总运行时间为0.11 s。图11即为单刃滚刀滚动力的时程曲线。图12～图14为单刃滚刀在初始顶进阶段(t=0.01 s)和掘进阶段(t=0.1 s)的应力分布图和位移分布图。

如图12所示，当滚刀间距为12 cm时，滚动力为最小；如图13所示的初始顶进阶段，滚刀间距在12～16 cm时等效应力为最大；如图14所示的刀盘掘进阶段，滚刀间距在16 cm时等效应力为最大，综合上述分析结果：砂卵石层所受最大等效应力均随滚刀间距的增加，呈先增大，后减小的变化趋势。由此可得滚刀间距取值范围定为12～16 cm之间，其破岩效果最佳。

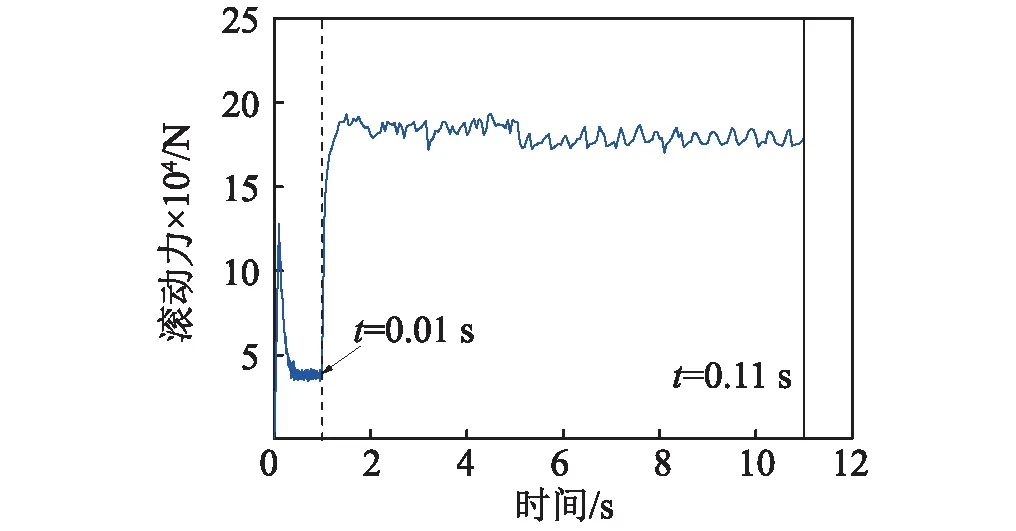
图11 单刃滚刀滚动力时程曲线 Fig.11 Single-faced hobbing rolling force time course

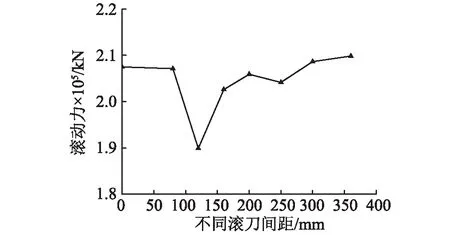
图12 滚刀间距与滚动力关系图 Fig.12 Relationship between hob spacing and rolling force

图13 滚刀间距与等效应力关系图(初始顶进阶段) Fig.13 The relationship between hob spacing and equivalent stress (initial jacking stage)

图14 滚刀间距与等效应力关系图(刀盘掘进阶段) Fig.14 Relationship between hob spacing and equivalent stress (cutterhead stage)

4 结 论

综合上述破岩机理、有限元仿真分析结果得出以下结论：

(1)切削速度与刮刀间距对刀具的水平切削力影响不大；切削深度对刀具水平切削力的显著。

(2)兰州地铁泥水盾构的刮刀切削角度(20.38°)具备良好的切削破岩效果，与仿真分析的刮刀切削角度20°相吻合，但切刀的切削深度不应多大，防止引起盘扭矩过大，出现刀盘过载现象。

(3)刀盘正面单刃滚刀的相邻滚刀间距过大，破岩效率过低，建议加密正面滚刀的布置数量，且滚刀间距取12～16 cm。

(4)为兰州地铁其他线路再次穿越黄河提供依据，对砂卵石地层盾构刀盘的设计提供参考。

[ 1 ] 钱七虎. 城市可持续发展与地下空间开发利用[J]. 地下空间,1998,18(2): 69-75.

QIAN Qihu. Sustainable development of the cities and the development and utilization of underground space [J]. Underground Space, 1998, 18(2): 69-75.

[ 2 ] 王梦恕. 21世纪我国隧道及地下空间发展的探讨[J]. 铁道科学工程学报, 2004, 1(1): 7-8.

WANG Mengshu. development of tunnel and underground space in 21th ccentury in china [J]. Journal of Rallway Science and Engineering, 2004, 1(1): 7-8.

[ 3 ] 王梦恕. 中国隧道及地下工程修建技术[M]. 北京: 人民交通出版社, 2010.

[ 4 ] 施仲衡, 全永燊, 马林. 以新的发展战略观迎接大城市交通问题的挑战[J]. 都市快轨交通, 2004, 17(3): 1-3.SHI Zhongheng, QUAN Yongshen, MA Lin. Facing the taiffc

challenge of megapolis with new development strategies [J].Urban Rapid Rail Transit, 2004, 17(3): 1-3.

[ 5 ] 施仲衡. 建设符合我国国情的地下铁道[J]. 都市快轨交通, 2013, 26(2): 24-25.

SHI Zhongheng. Building underground railway in line with china’s national conditions[J]. Urban Rapid Rail Transit, 2013, 26(2) : 24-25.

[ 6 ] 张载松. 盾构壁后注浆对隧道及地表沉降影响的研究[D]. 济南： 山东大学, 2014.

[ 7 ] 黄清飞. 砂卵石地层盾构刀盘刀具与土相互作用及其选型设计研究[D]. 北京： 北京交通大学, 2010.

[ 8 ] 张斌. 全断面岩石掘进机刀具磨损研究及刀具布局优化[D]. 天津： 天津大学, 2014.

[ 9 ] 吴玉厚, 田军兴, 孙健， 等. 基于ABAQUS的岩石节理特征对滚刀破岩影响研究[J]. 沈阳建筑大学学报(自然科学版), 2015, 31(3): 534-542.

WU Yuhou, TIAN Junxing, SUN Jian, et al. Effects of joint characteristics on rock breaking with dick cutter based on ABAQUS [J]. Journal of Shenyang Jianzhu University (Natural Science), 2015, 31(3): 534-542.

[10] 满林涛. 盘形滚刀破岩过程有限元数值模拟[D]. 大连： 大连理工大学, 2012.

[11] 张相琴, 张雪萍. Ti6A14V钛合金高速切削试验与有限元建模[J]. 机械设计与研究, 2012(4): 92-100.

ZHANG Xiangqin, ZHANG Xueping. Ti 6Al 4V High-speed cutting process experiment and finite element analysis[J]. Machine Design and Research, 2012(4): 92-100.

[12] 吴顺兴. 金属陶瓷刀具高速铣削超高强度钢铣削力及刀具磨损研究[D]. 长沙： 湖南科技大学, 2013.

[13] 刘锟. 硬岩隧道掘进机滚刀破岩仿真与磨损的研究[D]. 沈阳： 东北大学, 2013.

[14] 崔娟. 盾构机切刀切削过程模拟及刀盘扭矩计算方法[D]. 大连: 大连理工大学, 2012.

[15] 黄素霞, 李河宗, 崔坚, 等. 基于ABAQUS的金属切削数值模拟分析[J]. 工具技术, 2010, 44(2): 56-59.

HUANG Suxia, LI Hezong, CUI Jian, et al. Finite element analysis of metal cutting process by ABAQUS[J].Tool Engineering, 2010, 44(2): 56-59.

[16] 胡世军, 王瑞哲, 袁铭, 等. 硬态干式切削过程的有限元仿真[J]. 机械设计与制造, 2013(11): 139-141.

HU Shijun, WANG Ruizhe, YUAN Ming, et al. Finite element simulation of hard-dry cutting course[J]. Machinery Design and Manufacture, 2013(11): 139-141.

[17] 李娟. 盾构刀具的三维动态仿真研究[D]. 天津: 天津大学, 2008.

[18] 孙斌. TBM刀盘滚刀总体布局优化[D]. 天津: 天津大学, 2015.