地铁隔振措施对钢轨声功率特性影响测试分析

盛 曦， 赵才友， 王 平， 柯文华， 李成辉

(西南交通大学 高速铁路线路工程教育部重点实验室，成都 610031)

浮置板轨道和减振扣件轨道等隔振措施常设置在振动敏感地区，旨在隔离向环境土体传播的垂向振动能量[1-2]。然而，当列车通过该地段时会产生较大的车内噪声，影响乘客的舒适性。田建辉等[3]对中国某城市地铁1号线车内噪声进行测试分析，结果表明车内噪声主要集中在125～800 Hz的中低频段，并且列车经过普通道床时产生的噪声声压级小于橡胶浮置板道床和钢弹簧浮置板道床。肖安鑫等[4]通过现场测试发现，当列车经过钢弹簧浮置板地段时，车内噪声的连续等效A声级相比于普通轨道地段增大约3～5 dB，并在50～200 Hz范围内产生明显峰值。笔者对国内某城市地铁2号线车内噪声进行测试，发现当列车通过GJ-III型减振扣件长枕整体道床区段时，车内噪声明显高于普通轨道地段。隔振措施的采用会改变轨道的振动特性，影响滚动噪声，而滚动噪声是地铁车内噪声的重要组成部分[5]，因此研究常用隔振措施对滚动噪声的影响具有较大意义。

钢轨是1 600 Hz以下滚动噪声的主要声源[6]。轨道衰减率[7-8]定义为钢轨垂向或横向振动幅值随轨道纵向的衰减系数，反映了轨道结构对钢轨振动沿纵向的综合衰减能力，根据钢轨的振动方向分为垂向衰减率和横向衰减率。它已成为评判轨道声学特性的一个重要指标，控制着钢轨的有效声辐射长度。当钢轨振动速度幅值一定时，衰减率越大，振动沿钢轨纵向衰减得越快，钢轨的声功率也越低。国外学者对轨道衰减率进行了一系列研究[9]，并将轨道衰减率作为钢轨阻尼器的重要指标，研究阻尼器的降噪性能[10]。上述研究主要针对于有砟轨道，对无砟轨道乃至浮置板轨道的研究较少。孙晓静等[11]对比测试了剪切型减振器和DTVI2扣件两种轨道结构型式下的轨道衰减率和加速度导纳，分析研究了北京地铁特殊钢轨波磨的成因及整治措施。徐宁等[12]对南京地铁谐振式浮轨扣件进行衰减率和波磨测试，同时对比测试了I型扣件、DTVI2扣件和DTVII2扣件三种典型常用扣件。然而，上述研究并没有探究扣件对钢轨声辐射的影响。

本文对国内某城市地铁2号线钢弹簧浮置板轨道、减振垫浮置板轨道、GJ-III型减振扣件长轨枕整体道床及DZIII-1型扣件整体道床进行钢轨垂向振动沿纵向的轨道衰减率和钢轨加速度导纳测试，并结合测试结果计算分析了单位简谐点激励下的钢轨相对声功率级，研究常用轨道隔振措施对钢轨声功率特性的影响。

1 地铁常用隔振措施

本文选取了钢弹簧浮置板轨道、减振垫浮置板轨道、GJ-III型减振扣件长枕整体道床以及DZIII-1型扣件整体道床等轨道结构作为测试对象，四种轨道结构的示意图如图1所示。

(a)钢弹簧浮置板轨道

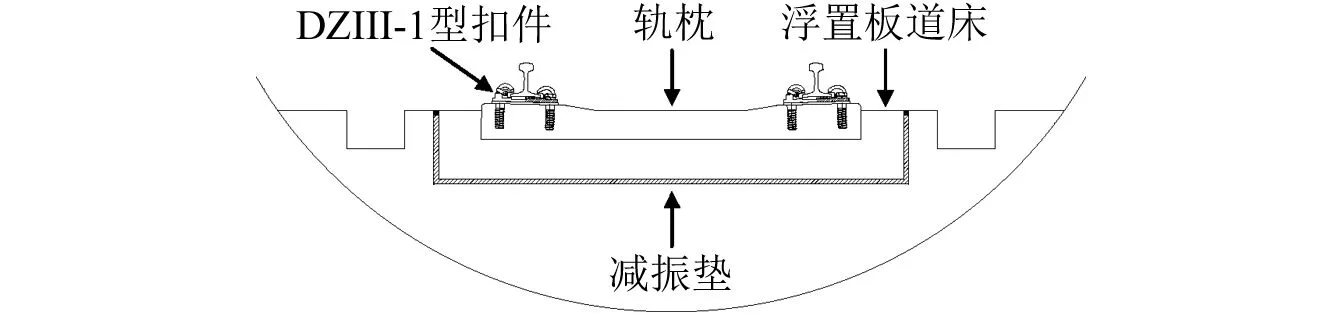
(b)减振垫浮置板轨道

(c)GJ-III型减振扣件长枕整体道床

(d)DZIII-1型扣件整体道床图1 四种轨道结构的示意图 Fig.1 Structural diagrams of four types of track

浮置板轨道系统是一种基于轨道结构改进方法的振源强度控制措施，普遍应用于具有较高减振要求的地段，其基本原理是在轨道与基础之间加入一个固有频率较低的质量-弹簧系统，隔离钢轨振动向基础结构的传递[13]。GJ-III型减振扣件通过设置双层非线性弹性垫板以降低系统垂向刚度并同时提高结构阻尼，实现减振目的[14]。DZIII-1型扣件长枕整体道床用于普通区段，该扣件减振性能较差且整体道床无减振效果，在本文中起对比作用。上述轨道结构主要参数如表1所示。

表1 测试轨道的结构参数Tab.1 Structural parameters of testing track

表1所示轨道隔振措施均降低了轨道的垂向刚度。钢弹簧浮置板道床和减振垫浮置板道床虽与普通整体道床同样采用DZIII-1型扣件，但板下支承刚度较小。GJ-III型减振扣件长枕整体道床和DZIII-1型扣件整体道床均为整体道床结构，但前者的扣件节点静刚度较小。由于文中将反复提及轨道结构名称，故在后文中将GJ-III型减振扣件长枕整体道床简称为GJ-III扣件轨道，DZIII-1型扣件长枕整体道床简称为DZIII-1扣件轨道，以求简洁。

2 测试方法与仪器

本文衰减率测试是依据规范EN15461：2008+A1：2010[8]进行的，在跨中轨头表面中心处布置加速度传感器，沿钢轨纵向在不同距离处分别垂向敲击轨头中心，通过各个锤击点的频响函数测试结果计算衰减率。测试步骤、锤点设置及计算公式详见该规范。测试采用拥有24位高精度模数转换器的东方所INV3018CT型采集仪，采样频率设置为12 800 Hz。激励力锤采用朗斯LC1302B型力锤，量程为50 kN，灵敏度为0.105 mV/N。传感器采用朗斯LC0102T型压电加速度传感器，工作频率范围2～13 000 Hz，灵敏度5 mV/g，量程为1 000 g。在各锤击点确保有五次有效锤击结果，最终结果取其平均值。为了获取准确的低频测试结果，在同一锤击点同时使用尼龙锤头和铝制锤头。不同锤头所得的频响函数相干系数,如图2所示。

图2 不同锤头的相干系数 Fig.2 Coherent coefficients of different hammer heads

由于频响函数的相干系数在分析频段内需控制在0.8以上[15]，因此铝制锤头的有效分析频率下限为100 Hz，而尼龙锤头的有效分析频率下限为30 Hz，故用尼龙锤头的低频测试结果去替代钢制锤头测试结果的相应部分以提高频响函数低频范围内的相干性。有效分析频率的上限满足激励力频谱幅值减少量不超过10 dB的限制要求[16]。测试分析频率范围为50～5 000 Hz，最大三分之一倍频程中心频率为4 000 Hz。

衰减率测试中第一个锤击点的频响函数测试结果即为钢轨加速度导纳。测试装置及锤点设置如图3所示。

(a)

(b)图3 测试装置及锤点设置 Fig.3 Test instrument and hammering point setup

3 测试结果

3.1 钢轨跨中垂向原点加速度导纳幅值

轨道的动态行为在滚动噪声的产生中起到重要的作用。钢轨原点加速度导纳是衰减率测试的关键基础，对了解钢轨振动特性，阐明衰减率曲线规律有着巨大的意义。四种轨道结构的钢轨跨中垂向原点加速度导纳幅值曲线和相干系数曲线如图4所示。

在50～100 Hz频段内，钢弹簧浮置板轨道、减振垫浮置板轨道和GJ-III扣件轨道钢轨加速度导纳幅值大于DZIII-1扣件轨道，这是因为钢弹簧、减振垫和GJ-III扣件所提供的垂向刚度较小。

在100～550 Hz频段内，四条曲线出现了明显的波峰和波谷。在180～260 Hz频率范围内，钢弹簧浮置板轨道、减振垫浮置板轨道以及DZIII-1扣件轨道的幅值曲线均出现了波谷，对应钢轨的反共振频率fa。三种轨道结构均采用了DZIII-1扣件，并且轨下基础完全不同(钢弹簧浮置板与减振垫浮置板尺寸不一，DZIII-1扣件轨道道床板与基底固结)，因此该波谷主要由扣件所产生，此频率下扣件系统吸收了钢轨振动能量，铁垫板振动剧烈，起着动力吸振器的作用，而这几十赫兹的频率差异主要是因为胶垫的实际刚度和扣件系统装配状态并不完全相同[16]。钢弹簧浮置板轨道在448 Hz(记为fr)出现钢轨共振模态，该共振频率主要由扣件垂向刚度所决定。对于减振垫浮置板轨道，fr为505 Hz；对于DZIII-1扣件轨道，fr为502 Hz。GJ-III型减振扣件由于其较低的垂向刚度，fr仅为161 Hz，远小于另外三种轨道结构。当频率高于fr时，钢轨中弹性波的传播主要与钢轨自身和扣件系统相关，道床的影响较小。在500～1 000 Hz频率范围内，GJ-III扣件轨道钢轨垂向加速度导纳幅值低于采用DZIII-1扣件的另外三种轨道结构。

(a)50～900 Hz

钢弹簧浮置板轨道、减振垫浮置板轨道、GJ-III扣件轨道、DZIII-1扣件轨道加速度导纳幅值曲线分别于1 036 Hz，1 036 Hz，1 022 Hz和1 023 Hz出现峰值。为了探究该共振频率下钢轨的振动特性，在DZIII-1扣件轨道跨中和相邻扣件处的轨头表面布置加速度传感器，垂向敲击钢轨跨中，计算原点加速度导纳和传递加速度导纳，结果如图5所示。

图5 垂向原点和传递加速度导纳测试结果 Fig.5 Vertical direct acceleration mobility and transfer acceleration mobility

在该共振频率下，跨中处的原点加速度导纳幅值为极大值，而扣件处的传递加速度导纳幅值并未出现峰值，并且两者相位差约为90°，因此该频率为钢轨一阶垂向弯曲pinned-pinned频率(记为fp)，其共振模态对应于扣件处为节点的驻波。高于此频率，四种轨道结构钢轨加速度导纳幅值相差不大。在2 700 Hz附近，幅值曲线均出现谷值，钢轨发生二阶垂向弯曲pinned-pinned共振(记为fp2)，该频率下在一个扣件间距内包含一个完整的波形，钢轨跨中和扣件处均为驻波节点。

3.2 钢轨垂向振动衰减率

四种轨道结构钢轨垂向振动沿纵向的轨道衰减率如图6所示。

3.2.1 钢弹簧浮置板轨道钢轨垂向振动衰减率

在中心频率50～100 Hz范围内，钢弹簧浮置板轨道维持着较高的垂向衰减率。在中心频率50 Hz时，衰减率为8.5 dB/m。随着频率的增大，浮置板的振动减弱，更多垂向振动能量沿钢轨纵向传播出去，衰减率开始降低。在中心频率250 Hz处，衰减率为2.7 dB/m。

(a)50～800 Hz

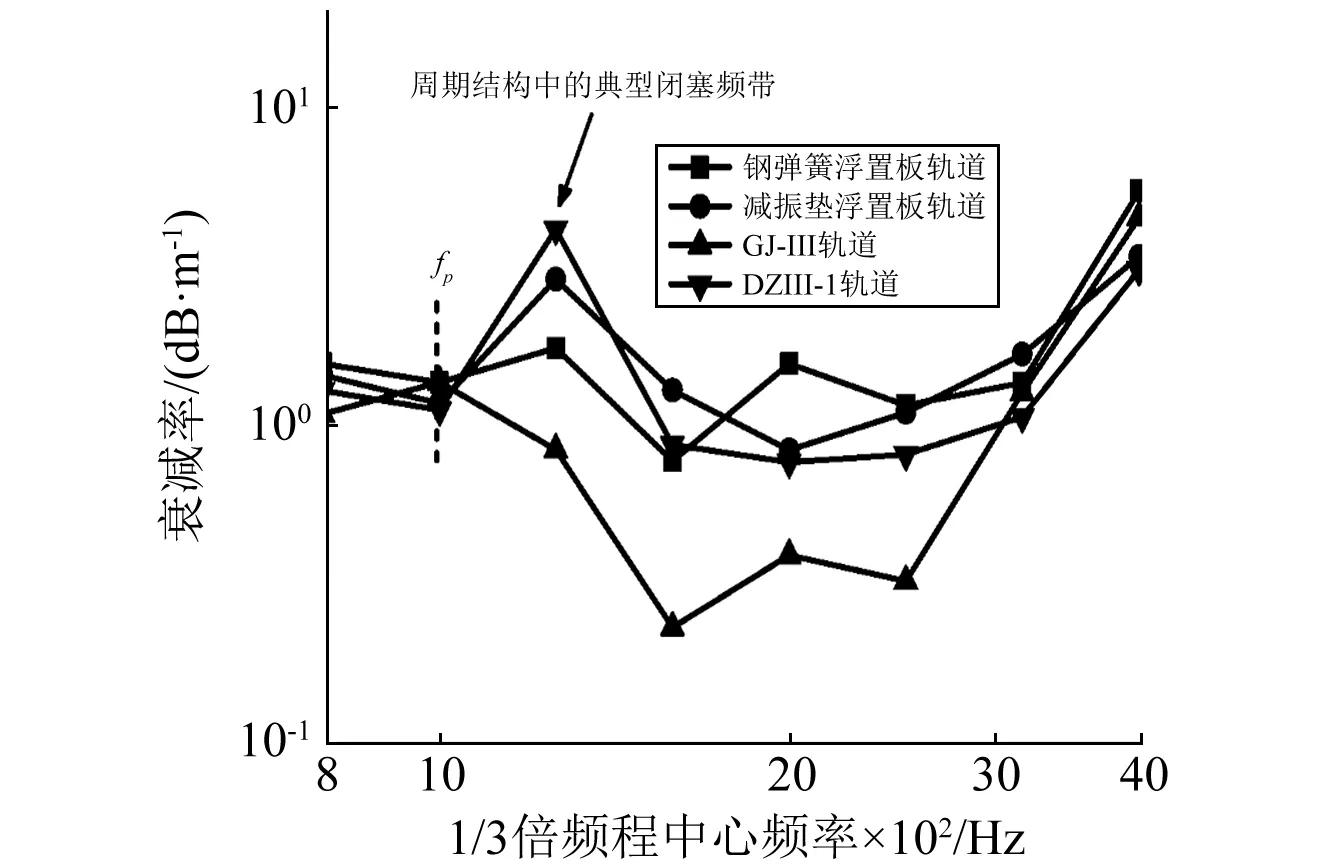
(b)800～4 000 Hz图6 四种轨道结构钢轨垂向振动沿纵向的衰减率 Fig.6 Vertical track decay rates of four types of track

反共振频率fa和共振频率fr组成了钢轨中沿纵向传播的弹性波的“闭塞”区边界频率，在该频段内频率未到达钢轨的截止频率(即共振频率fr)，弹性波的传播受到抑制，轨道衰减率逐渐增大并维持在较高数值，在中心频率400 Hz出现极值9.4 dB/m。由于反共振频率fa和共振频率fr均由扣件系统所决定，因而该“闭塞”区的产生主要是因为扣件系统的作用。当频率高于fr时，轨道衰减率随着频率的增大而降低。由于钢轨的一阶垂向pinned-pinned弯曲共振，衰减率在中心频率1 000 Hz出现波谷。当频率高于fp并继续增大时，衰减率回升并出现一个较小的波峰，这是由于该频带为周期结构中的典型闭塞频带[17]，即使不存在阻尼仍发生衰减。当中心频率大于1 600 Hz，轨道衰减率呈现增大的趋势。轨道衰减率在接近5 000 Hz时逐渐达到峰值，钢轨轨底发生摆动模态。

3.2.2 减振垫浮置板轨道钢轨垂向振动衰减率

减振垫浮置板轨道钢轨垂向振动衰减率变化规律同钢弹簧浮置板轨道一致。在中心频率50 Hz处，衰减率为5.1 dB/m。在中心频率400 Hz处，衰减率出现极值6.9 dB/m。同样地，减振垫浮置板轨道衰减率曲线在中心频率1 000 Hz处出现波谷。在2 000 Hz频率以上时，衰减率逐渐增大。

由图6测试结果可知，在中心频率50～200 Hz范围内，钢弹簧浮置板轨道和减振垫浮置板轨道衰减率均大于DZIII-1扣件轨道，这是因为浮置板振动较为剧烈，大量吸收了钢轨的振动能量，故轨道衰减率高于DZIII-1扣件轨道。而当中心频率增大到200 Hz时，浮置板的作用逐渐减弱。由于DZIII-1轨道的反共振频率fa最小，其衰减率曲线率先进入“闭塞”区，轨道衰减率的增大提前于钢弹簧浮置板轨道和减振垫浮置板轨道，因而在中心频率200～400 Hz范围内，两种浮置板轨道的衰减率均小于DZIII-1扣件轨道。当中心频率大于500 Hz，钢弹簧浮置板轨道和减振垫浮置板轨道衰减率与DZIII-1扣件轨道差别不大。板下支承刚度对中高频轨道衰减率的影响不大。

对比钢弹簧浮置板轨道和减振垫浮置板轨道衰减率可知，在中心频率50～500 Hz范围内，减振垫浮置板轨道衰减率小于钢弹簧浮置板轨道。

3.2.3 GJ-III扣件轨道钢轨垂向振动衰减率

GJ-III扣件轨道衰减率在中心频率2 500 Hz以下几乎均小于DZIII-1扣件轨道，并维持在较小的数值范围内，因此该扣件对钢轨垂向振动沿纵向传播的衰减能力不及DZIII-1扣件。GJ-III型减振扣件垂向刚度较低，减弱了钢轨与道床之间的耦合连接，故垂向振动能量主要沿钢轨纵向传播，其衰减率较小。

GJ-III型减振扣件的低垂向刚度使“闭塞”区出现在中心频率200 Hz以下，并且在中心频率126 Hz处的极值也仅为3.3 dB/m。在中心频率3 160 Hz以上，衰减率与DZIII-1扣件轨道相差不大。扣件系统对高频轨道衰减率的影响较小。

4 钢轨垂向振动相对声功率级

钢轨振动的声功率反映了滚动噪声中钢轨声能的大小，由衰减率和其他多种因素共同决定，与受声者的位置无关。本节通过钢轨垂向振动沿纵向的轨道衰减率和钢轨加速度导纳测试结果，计算单位简谐点激励下的钢轨相对声功率级。

无限长钢轨的声功率W可表示为：

(1)

式中：v(x)是钢轨在x处振动速度的幅值，ρ0c0为空气中的声特性阻抗，ρ0=1.225 kg/m3为空气密度，c0=340 m/s为声波在空气中的传播速度，σ是与频率有关的辐射率[18]，为钢轨的固有属性，P为一个截面的周长，对于钢轨垂向振动，该值为钢轨轨底及轨头的顶部和底部宽度之和[6]，即0.413 m。

假设钢轨的垂向振动沿着线路纵向以随距离呈指数衰减的形式而传播：

|v(x)|=v(0)e-β|x|

(2)

其中v(0)为参考点处的振动速度幅值，β为衰减系数。利用线路前后方向的对称性，于是：

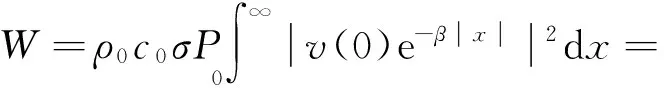
(3)

将衰减系数转变成以dB/m为单位的衰减率形式，Δ=8.686βdB/m，则

(4)

以W0=10-12W为基准声功率，可将声功率表示成声功率级：

(5)

式(5)表明轨道衰减率越大，钢轨声功率级越低，钢轨导纳幅值越大，钢轨声功率级越高。本文中的四种轨道结构均为无砟轨道，有着相同的扣件间距以及胶垫支承面积。于是若将钢轨简化为线声源，可认为其辐射率相同。同时，空气声特性阻抗以及钢轨截面周长也都一致。故式(5)第一项对于四种轨道结构均相同。在某一频率f下，加速度导纳幅值为导纳幅值的2πf倍，故可利用加速度导纳幅值测试结果求得四种轨道结构的导纳幅值。再结合衰减率测试结果及式(5)，以DZIII-1扣件轨道钢轨声功率级作为参考声功率级，可得单位简谐点激励力作用下三种减振型轨道钢轨相对声功率级，并以三分之一倍频程形式表示，如图7所示。

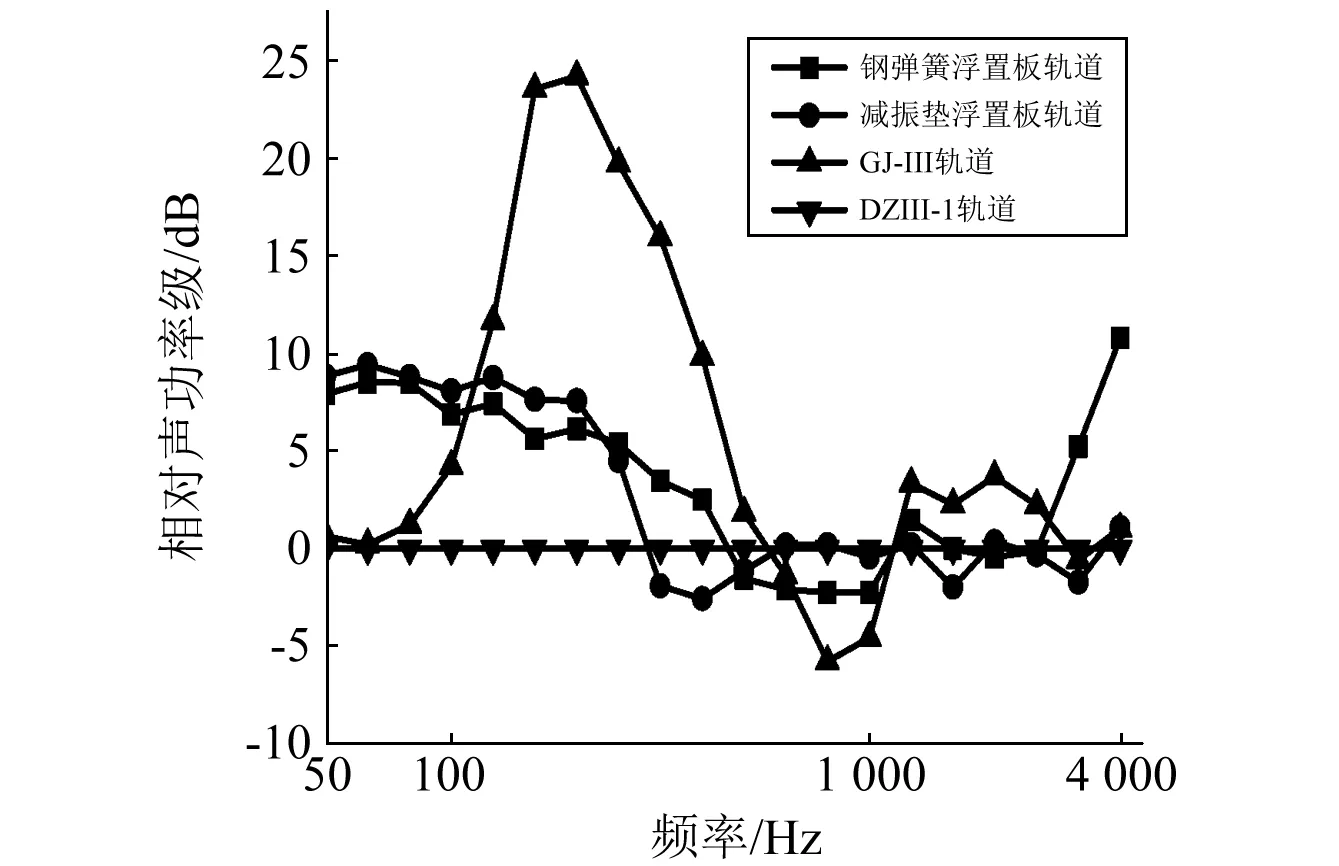
图7 三分之一倍频程下三种减振型轨道钢轨相对声功率级 Fig.7 Relative rail sound power levels of three types of vibration-reduction track

尽管在50～200 Hz频率范围，浮置板轨道有着较高的衰减率，但由于其较大的钢轨导纳幅值，在单位简谐单点激励力作用下，浮置板轨道钢轨声功率级明显大于DZIII-1扣件轨道。钢弹簧浮置板轨道在200～400 Hz范围内(对于减振垫浮置板轨道为200～300 Hz)有着较低的衰减率，使得钢轨声功率级同样大于DZIII-1扣件轨道。钢弹簧浮置板轨道200 Hz以下的钢轨相对声功率级在5 dB以上，而减振垫浮置板轨道200 Hz以下的钢轨相对声功率级在7 dB以上。在400 Hz以上时，浮置板轨道钢轨声功率级与DZIII-1扣件轨道相差不大。

对于GJ-III扣件轨道，在中心频率80 Hz范围以下，其钢轨声功率级与DZIII-1扣件轨道相差不大。在中心频率80～500 Hz范围内，由于钢轨导纳幅值曲线出现波峰并且垂向衰减率极低，使其钢轨声功率级远大于DZIII-1扣件轨道，在中心频率200 Hz处，差值高达24 dB。

本文所测试的浮置板道床和减振型扣件等轨道隔振措施降低了轨道垂向刚度，改变了钢轨垂向振动的加速度导纳幅值和衰减率，使更多的中低频能量沿着钢轨纵向传播，并以声能的形式向外传播。因此，可通过在减振区段钢轨上设置阻尼器，减少钢轨声辐射及滚动噪声。

5 结 论

本文对钢弹簧浮置板道床、减振垫浮置板道床、GJ-III型减振扣件长轨枕整体道床及DZIII-1型扣件整体道床进行了衰减率和钢轨加速度导纳测试，并结合测试结果计算分析了单位简谐点激励下的钢轨相对声功率级，结论如下：

(1)在三分之一倍频程中心频率50～200 Hz范围内，由于浮置板的参振作用，钢弹簧浮置板轨道和减振垫浮置板轨道垂向衰减率均大于DZIII-1扣件轨道。当中心频率高于200 Hz时，浮置板道床的参振作用减弱，此时轨道衰减率主要受板上扣件影响。

(2)GJ-III型减振扣件的较低垂向刚度，减弱了钢轨与道床之间的耦合连接，使得轨道衰减率在中心频率2 500 Hz以下均小于DZIII-1型扣件轨道，并维持在较小的数值范围内。钢轨加速度导纳幅值同样因轨道刚度的降低而发生变化。

(3)隔振措施通过降低轨道垂向刚度而实现减振，然而刚度的变化同样改变了钢轨垂向振动的加速度导纳幅值和衰减率，影响了钢轨声功率。在单位简谐点激励下，由于浮置板道床的影响，钢弹簧浮置板轨道和减振垫浮置板轨道在50～200 Hz范围内钢轨的垂向声功率级明显高于DZIII-1扣件轨道，而GJ-III型减振扣件轨道在80～500 Hz范围内明显高于DZIII-1扣件轨道。

[ 1 ] 刘鹏辉，杨宜谦，尹京. 地铁隧道内不同轨道结构振动测试与分析[J]. 振动与冲击，2014, 33(2)：31-36.

LIU Penghui, YANG Yiqian,YIN Jing. Test and analysis on vibration of different track structures in tunnel[J]. Journal of Vibration and Shock, 2014, 33(2): 31-36.

[ 2 ] 吴宗臻，刘维宁，马龙祥，等. 地铁浮置式轨道引起地表振动响应解析预测模型研究[J]. 振动与冲击， 2014， 33(17)： 132-137.

WU Zongzhen, LIU Weining, MA Longxiang, at al. Analytical prediction of ground vibration response induced by metro floationg-type track[J]. Journal of Vibration and Shock, 2014, 33(17): 132-137.

[ 3 ] 田建辉，李兵，简炼.不同道床对地铁车内噪声影响特性分析[J]. 噪声与振动控制, 2015， 35(6): 105-109.

TIAN Jianhui, LI Bing, JIAN Lian. Analysis of metro interior noise characteristics for different track beds[J]. Noise and Vibration Control, 2015, 35(6): 105-109.

[ 4 ] 肖安鑫，田野. 钢弹簧浮置板轨道对车内噪声影响的实测和分析[J]. 噪声与振动控制， 2012， 32(1): 51-54.

XIAO Anxin, TIAN Ye. Measurement and analysis of influence of steel spring floating slab track on vehicle interior noise[J]. Noise and Vibration Control, 2012， 32(1): 51-54.

[ 5 ] 任海，肖友刚. 地铁车内噪声的成因及控制策略[J]. 铁道车辆， 2009， 47(4): 25-28.

REN Hai, XIAO Yougang. The cause and control strategy of vehicle interior noise[J]. Rolling Stock, 2009, 47(4): 25-28.

[ 6 ] THOMPSON D J. Railway noise and vibration: mechanisms, modeling and means of control[M]. Oxford: Elsevier, 2009: 20-24, 51-58, 76-81, 195-196.

[ 7 ] JONES C J C , THOMPSON D J, DIEHL R J. The use of decay rates to analyse the performance of railway track in rolling noise generation[J]. Journal of Sound and Vibration, 2006, 293(3/4/5): 485-495.

[ 8 ] CEN. BS EN 15461: 2008+A1: 2010 Railway Applications-Noise Emission-Characterization of the Dynamic Properties of Track Selections for Pass by Noise Measurements[S]. Brussels: CEN Management Centre, 2010.

[ 9 ] RHUE J, THOMPSON D J, WHITE P R, at al. Decay rates of propagating waves in railway tracks at high frequencies[J]. Journal of Sound and Vibration, 2009, 320(4): 955-976.

[10] MAES J, SOL H. A double tuned rail damper-increased damping at the twofirst pinned-pinned frequencies[J]. Journal of Sound and Vibration, 2003, 267(3): 721-737.

[11] 孙晓静，张厚贵，刘维宁，等. 轨道系统钢轨振动衰减率动力测试研究[J]. 铁道工程学报， 2015， 32(7): 34-39.

SUN Xiaojing, ZHANG Hougui, LIU Weining, at al. Test research on the characterizing the dynamic damping behavior of track structure[J]. Journal of Railway Engineering Society, 2015， 32(7): 34-39.

[12] 徐宁, 王志强, 张攀, 等. 谐振式浮轨扣件减振性能测试研究[J]. 材料开发与应用， 2014， 29(6): 22-26.

XU Ning, WANG Zhiqiang, ZHANG Pan, at, al. Study on damping performance of tuned damper floating rail fastener[J]. Development and Application of Materials, 2014， 29(6): 22-26.

[13] 李增光，吴天行. 浮置板轨道二维建模及隔振性能分析[J]. 铁道学报， 2011， 33(8): 93-98.

LI Zengguang, WU Tianxing. 2-D Modeling of floating slab rrack and performance analysis on vibration isolation[J]. Journal of the China Railway Society, 2011， 33(8): 93-98.

[14] 王志强， 王安斌， 白健， 等. 成都地铁轨道GJ-III型减振扣件振动控制效果分析[J]. 噪声与振动控制， 2014， 34(3): 190-194.

WANG Zhiqiang, WANG Anbin, BAI Jian, at al. Experimental study on track vibration control using GJ-III rail fastening system in Chengdu Metro[J]. Noise and Vibration Control, 2014, 34(3): 190-194.

[15] THOMPSON D J, VINCENT N. Track dynamic behavior at high frequencies. Part 1: Throretical models and laboratory measurement[J]. Vehicle System Dynamics, 1995, 24(Sup1): 86-99.

[16] MAN A P D. A survey of dynamic railway track properties and theirquality[D]. Delft: TU Delft, 2002: 21-50.

[17] MEAD D J. Wave propagation and natural modes in periodic systems: I. Mono-coupled systems[J]. Journal of Sound and Vibration, 1975, 40(1): 1-18.

[18] 万淑敏，吴天行. 铁路钢轨垂向振动的声辐射分析[J]. 噪声与振动控制， 2009， 29(3)： 86-89.

WAN Shuming, WU Tianxing. Analysis of Rail Acoustic Radiation due to Vertical Vibration[J]. Noise and Vibration Control, 2009， 29(3)： 86-89.