基于分块多向主成分分析的翻车机液压系统故障诊断

鄂东辰 张立杰

1.燕山大学河北省重型机械流体动力传输与控制实验室，秦皇岛，0660042.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004

0 引言

翻车机是用于火车卸料，具有周期性工作特点的大型生产设备。它将满载的车厢翻转160°使散料从车厢中卸出，其中液压系统的作用是把车厢固定夹紧在翻车机轨道上，避免翻转过程中发生脱落。由于翻车机工作环境恶劣使液压系统经常出现泄漏和阻塞等故障，影响港口物料的正常输送，因此有必要对翻车机液压系统的工作过程进行故障监测与诊断。故障监测可以分为基于物理模型和统计模型两大类。由于在物理建模过程中需要做大量的假设和简化，使得物理模型的精度受到一定程度的影响。本文从监测数据的角度出发，建立了翻车机液压系统工作过程的统计模型，对其故障进行统计推断。主成分分析(principal component analysis, PCA)方法是常用的多元统计分析方法[1-2]，主要应用在具有连续稳定工作性质的化工设备状态监测中[3-4]。由于翻车机液压系统的工作过程具有多工步和时变性的特点[5]，本文采用多向主成分分析(mulitway principal component analysis, MPCA)方法[6]对其工作过程的每个时间点分别进行建模和监测。

常规的MPCA方法应用全部监测变量建立各工步的统计模型，这种方法虽然可以用一个模型对整个系统进行监测，但是由过多实际不相关的变量建立的统计模型会弱化原本具有物理意义的变量间的因果关系，使得基于该模型的故障监测和诊断精度降低。由于翻车机液压系统在不同工步参与工作的监测变量不同，本文提出对每个工步参与工作并且具有直接因果关系的变量进行分组，建立多块MPCA模型，并将其应用在翻车机液压在线故障监测与诊断系统当中。

1 物理建模

1.1 翻车机液压系统工作原理

某港口C80型翻车机采用两节车厢同时翻转卸料。翻车机液压系统按照液压缸的布置方式可以分为压车部分和靠车部分。压车部分系统见图1，它由开式侧和闭式侧两部分组成。在开式侧系统中共有4个并联的液压缸(2.1，2.2,2.3，2.4)，称为压车缸。每个压车缸有杆腔布置了一个液控单向阀(1.1,1.2,1.3,1.4)。主换向阀10.1控制压车缸压下或抬升。在主换向阀与压车支路之间设置了主单向阀(9.1，9.2，9.3)，由阀8.1控制开启。缸5.1称为补偿缸。闭式侧包含压车和靠车部分，压车部分由6个并联的压车缸组成，其工作原理与开式侧相一致。文中以压车系统为例，靠车部位未示出。在工作过程中，开式侧和闭式侧压车缸同时动作。由2.1、2.2、2.5、2.6、2.7号压车缸共同托住一节车厢，另外5个缸托住第二节车厢。整个压车系统中共布置了18个测压点(p1,p2,…，p18)，如图1所示。

根据翻车机液压系统在一个工作周期内的不同工步将其分为4个阶段，即压下阶段、释放阶段、保压阶段和抬升阶段。在压下阶段液压缸空载动作将车厢固定在轨道上。翻转角度0°<θ<90°时为释放阶段，压车缸与补偿缸串联使压车缸活塞略微抬起，释放车厢底部弹簧的弹性势能。90°<θ<160°时为保压阶段，依靠单向阀(1.1,1.2,…，1.10)将压车缸保压。在抬升阶段压车缸差动连接将压车梁迅速抬升复位。表1为一个工作周期内压车系统电磁铁动作顺序表。

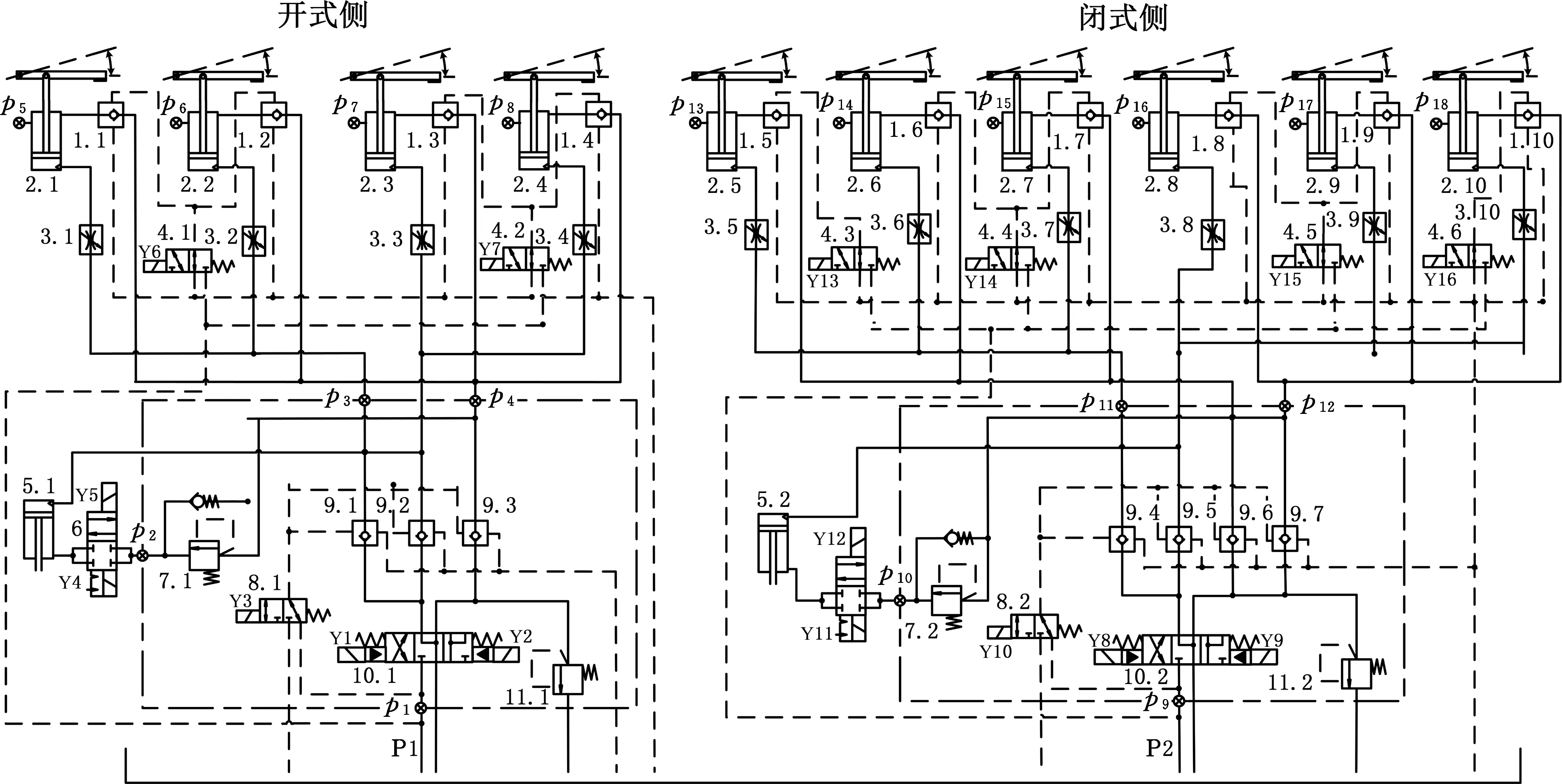
图1 翻车机液压系统压车部分Fig.1 The vertical holding devices in hydraulic system of car dumper

阶段Y1Y2Y3Y4Y5Y6Y7Y8Y9Y10Y11Y12Y13Y14Y15Y16压下+-++-+++-++-++++释放----+++----+++++保压---+------+-----抬升-++-+++-++-+++++

1.2 卸料过程的物理建模

由极点法理论可知，重力卸料的瞬间装载线是对数螺旋线[7]，其极坐标方程为

R=R0e-θtanφ

(1)

极距H计算公式为

H=g/ω2

(2)

极坐标方程转化为直角坐标系下方程：

(3)

式中，(θ,R)为极坐标；φ为散煤安息角；g为重力加速度；ω为角速度；(xP,yP)为极点坐标；R0为极点P到车厢上沿C点的距离；θCP为R0与x轴夹角。

由于极距是车厢宽度的10倍以上，故可以用对数螺旋线在C点处的切线近似代替物料的瞬时装载线。由式(3)得

(4)

由于θ=0°且θCP≈90°，k=-tanφ,因此，切线斜率等于物料的安息角。当散煤经过该切线后，其极限平衡被打破，开始滑落出车厢。

翻车机卸料过程中车厢主要承受重力、压车缸和靠车缸支反力、弹簧弹力和靠车板与车厢侧壁之间的摩擦力，如图2所示。根据翻车机液压系统卸料过程的机理，再将释放阶段分为θ<φ、φ<θ<42°和θ>42°三个阶段。其中φ=32°[8]、φ=42°为顺序阀(7.1)开启对应的翻转角度。当θ<φ时无煤卸出，压车缸主要承受因车厢重心偏移释放的弹性势能；当φ<θ<42°时煤开始卸出，弹簧释放的弹性势能包含重心偏移和重力减小两部分；当42°<θ<90°时压车缸压力大于顺序阀的开启压力10 MPa，使补偿缸动作，压力保持恒定。保压阶段又可分为θ<90°+φ和θ>90°+φ两个阶段。当90°<θ<90°+φ时压车缸承受剩余煤的重力和弹簧释放的弹性势能。当90°+φ<θ<160°时煤已经全部卸出，压车缸承受车皮自重和弹簧释放的弹性势能。

各阶段翻车角度与开式侧压车缸有杆腔压力的关系模型如表2所示，2 MPa为压下阶段泵出口溢流阀的调定压力，参数的名称及数值见表3。由车厢中散煤的横截面积随θ减小的关系推导卸料过程剩余煤质量的计算公式为

m′=m-2b2tan(θ-φ)lρ/2

(5)

m″=m-[2b-htan(90°+φ-θ)]hlρ/2

(6)

式中，m′和m″分别为车厢中剩余煤的横截面积为梯形和三角形的质量。

图2 车厢受力分析Fig.2 Force analysis of car

翻转角度压车缸有杆腔压力(MPa)0°～φ5Lm[(1-cosθ)-μsinθ]/(2S)+2φ～42°5L(m-m'cosθ-μm'sinθ)/(2S)+242°～90°1090°～90°+φ5Lm″(cosθ-μsinθ)/(2S)+1090°+φ～160°5Lm0(cosθ-μsinθ)/(2S)+10

表3 模型参数

1.3 模型误差分析

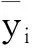
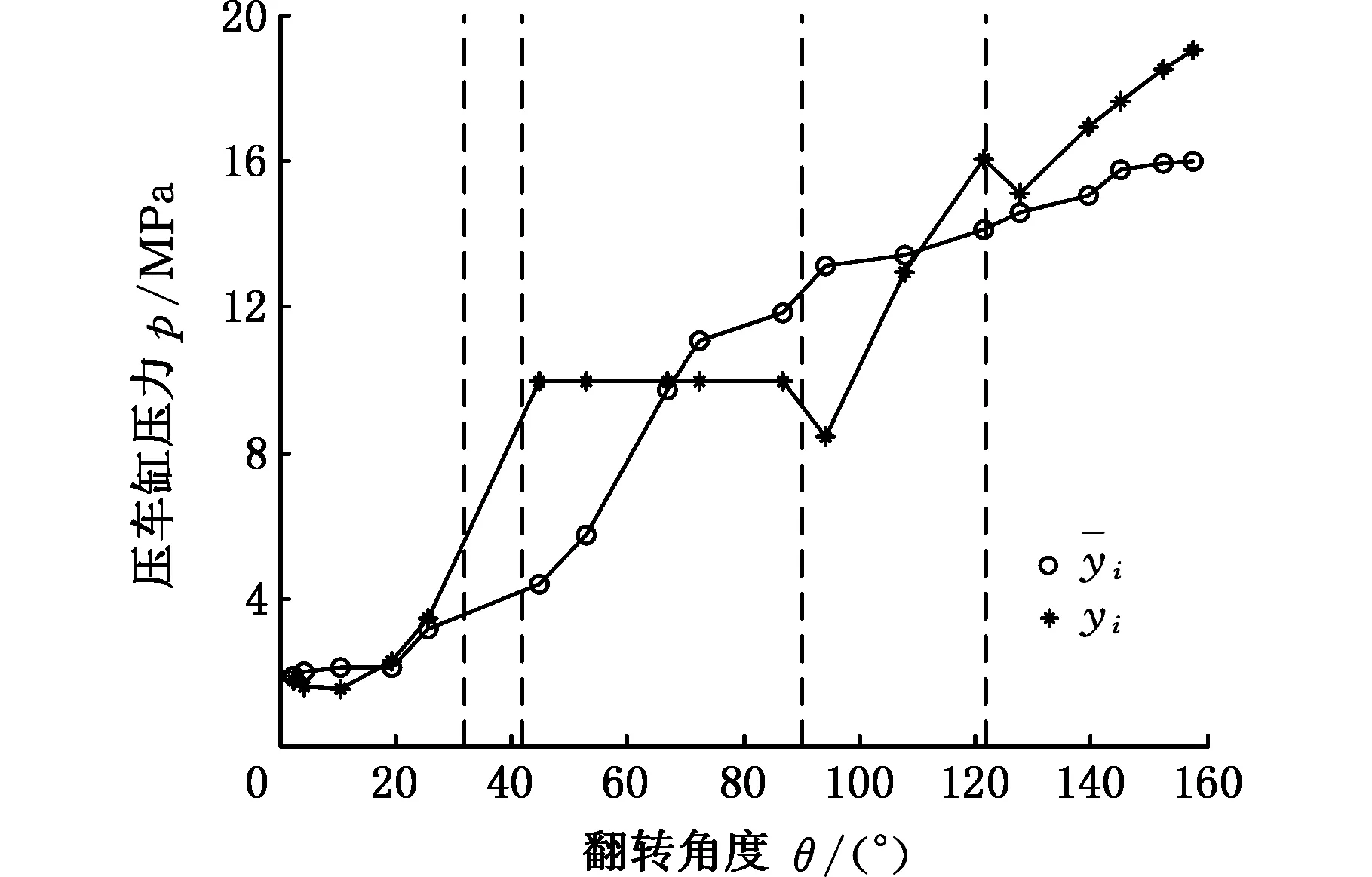
图3 模型计算结果与实测曲线Fig.3 The results of model and measured values

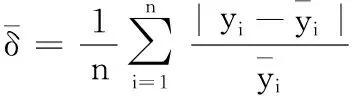
(7)

其中，n为阶段内的监测点数。计算结果见表4。

表4 模型误差

由于建立的物理模型难以满足实际中对翻车机液压系统故障监测的精度要求，故本文采用数据驱动的统计推断方法对其进行故障监测。

2 MPCA建模及监测

2.1 监测时刻选取

翻车机每工作一个周期需要50～60 s，其用时不相等。如果用时间作为子PCA的识别标记会造成监测时刻与模型错位。本文以电磁铁Y1和Y2得电后的时刻作为压下和抬升阶段的子PCA识别标记；以翻转角度和正反转信号作为释放和保压阶段的子PCA识别标记。一个生产周期共建立了31个子PCA模型，其监测时段如图4中的阴影部分所示。

图4 一个生产周期内的监测时间段Fig.4 Monitoring time segments in one working cycle

2.2 各阶段MPCA子模型变量分块

以系统中的18个压力信号和翻转角度信号作为监测变量。根据翻车机压车系统的工作机理对不同阶段的监测变量进行分块，并且排除在该阶段不参加工作的测点，分块结果如表5所示。

表5 变量分块

2.3 MPCA建模

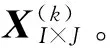
(8)

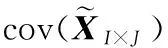
根据特征值的累加贡献率，将P分成主成分空间和残差空间:

(9)

式中，q为主成分个数;λi为特征值;85%为设定的阈值。

通过特征值分解可以找到数据中方差变化最大的方向pi(i=1，2，…，q)和在其上的投影ti(i=1，2，…，q)，即所谓的统计模型。

2.4 基于MPCA的状态监测

基于MPCA的监测是通过Hotelling-T2和SPE(squared prediction error)两个统计量对监测数据是否符合建模数据的分布特征进行假设检验，从而间接对系统工作状态做出判断。T2统计量反映监测变量均值的变化情况，当系统外负载发生变化时也会使T2超出控制限，而系统中并不存在故障。SPE统计量反映监测变量间的相关关系的变化，只要SPE超出控制限则认为系统中发生故障。因此，本文仅以SPE统计量作为故障判断指标。

SPE定义为监测变量在残差空间投影的平方和，即

SPE=EET

(10)

E=x(I-PPT)

式中，E为监测数据x在残差空间的投影；I为单位矩阵。

SPE统计量控制限为[10]

(11)

式中，Cα为标准正态分布下显著性水平为α的分位点。

2.5 分块MPCA监测方法流程

完整的分块MPCA故障监测流程如图5所示。其中，SPE(i)表示第i个子块的SPE结果。

图5 方法流程Fig.5 Method process

3 压车缸泄漏故障下的监测结果分析

翻车机液压系统由多个压车缸共同承担刚体重力，使泄漏故障不易从外观上察觉。泄漏会使有载缸的压力减小，图6所示为保压阶段2.1号压车缸泄漏导致的压力曲线相对正常值发生漂移性递减的情况。2.1号缸泄漏使负载由2.2、2.5、2.6、2.7缸分担，由于2.2号缸与2.1号缸同在开式侧，故其压力增大的偏移量为2.1号缸偏离量值的一半，2.5、2.6、2.7号缸压力偏移量为2.1号缸的1/6。阴影部分为正常值加减对应的3倍标准差。图7所示为泄漏导致的压力曲线相对正常值发生不同程度的阶跃偏移变化情况，σ为标准差。

(a)2.1号缸

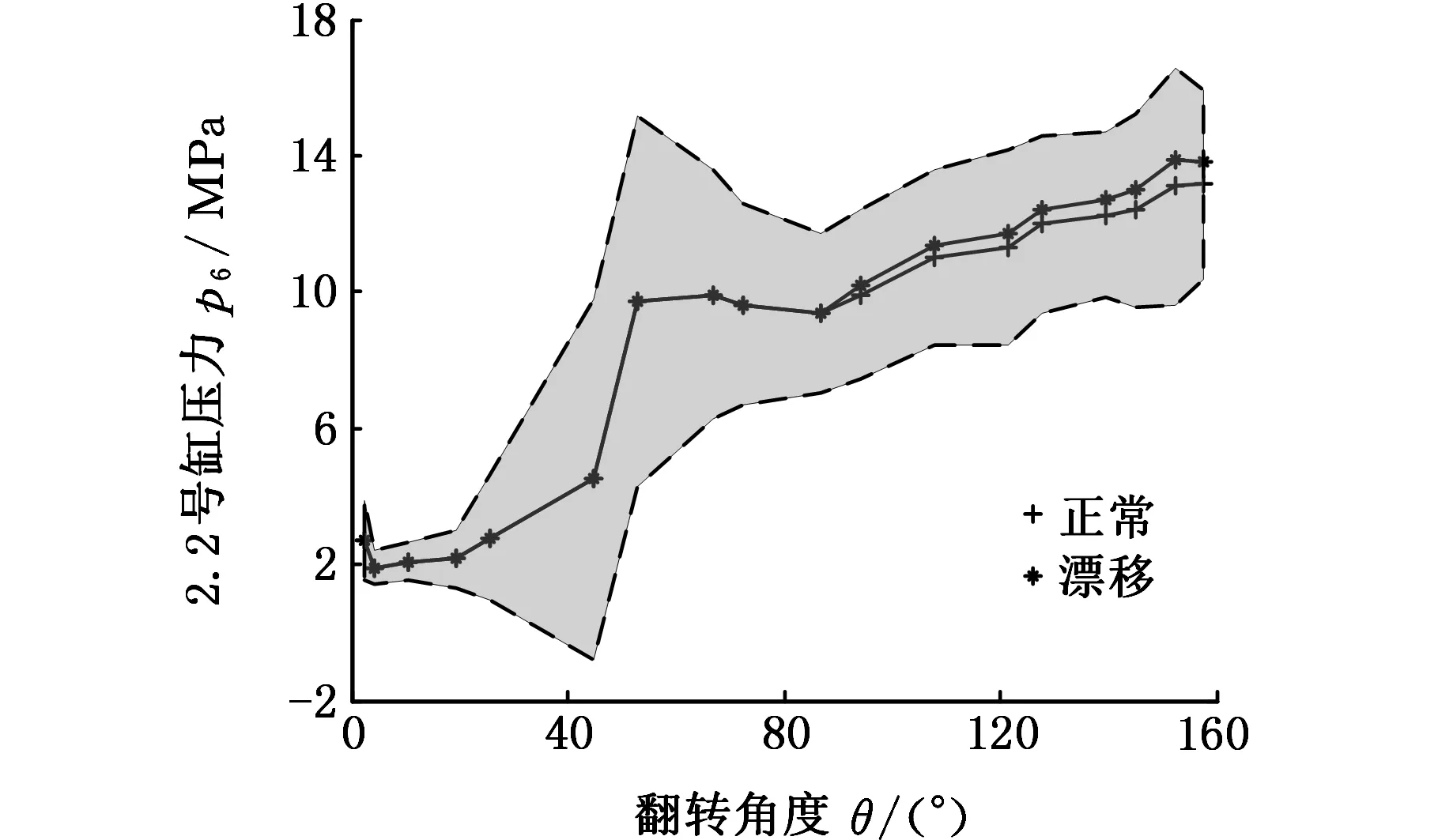
(b)2.2号缸图6 液压缸泄漏压力漂移曲线Fig.6 Pressure drifting curves of hydraulic cylinder with leakage fault

3.1 物理模型监测结果

基于物理模型对泄漏导致的p5逐渐漂移减小的监测结果如图8所示。在保压阶段p5实测曲线未连续超出以模型计算结果为中心的3倍标准差，监测系统认为压力在正常波动范围内，未监测到故障发生。

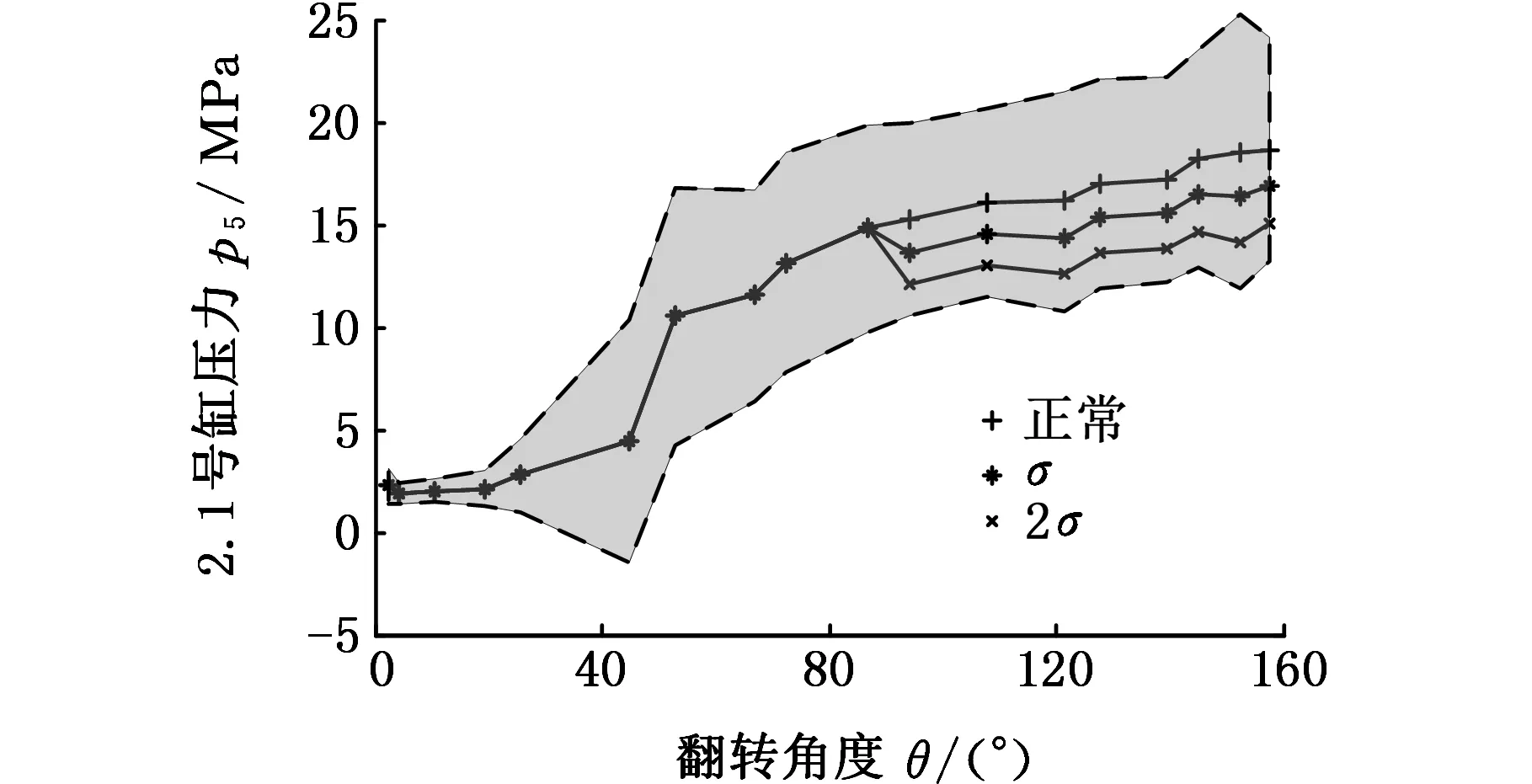
(a)2.1号缸

(b)2.2号缸图7 液压缸泄漏压力偏移曲线Fig.7 Pressure bias curves of hydraulic cylinder with leakage fault

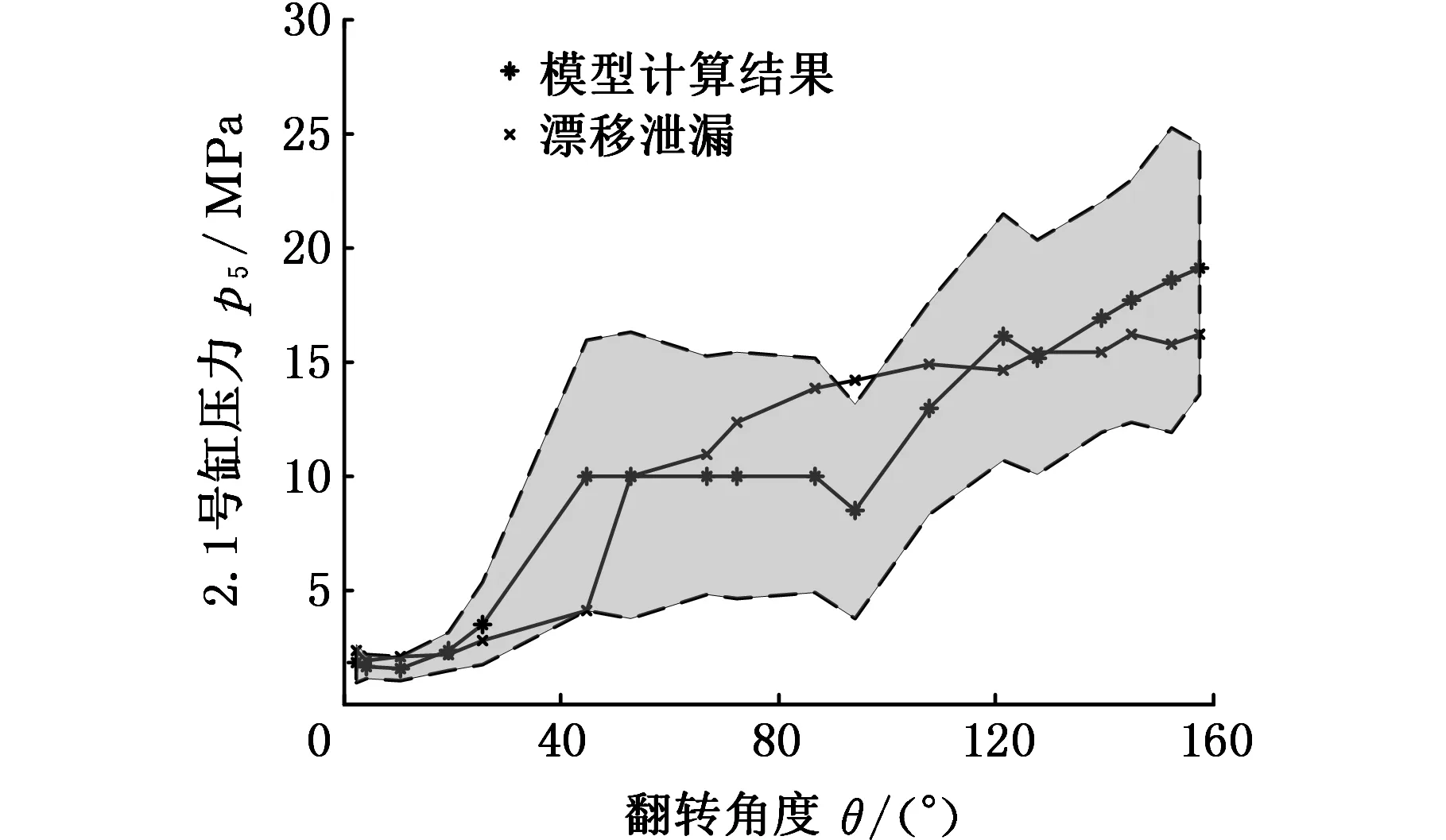
图8 基于物理模型对漂移泄漏的监测结果Fig.8 The monitoring result based on physical model for drifting leakage fault

3.2 MPCA监测结果

采用本文提出的分块MPCA模型和全变量MPCA模型对泄漏故障进行统计推断。在保压阶段，以变量(p5,p6,p13～p15,θ)构成一个子块，全变量建模取变量(p5～p8,p13～p18,θ)计算统计模型。泄漏导致压力逐渐漂移的监测结果如图9所示，图中点划线为置信度为95%的控制限。分块MPCA模型在偏差增至0.9倍标准差时监测到故障；全变量MPCA模型在偏差增至1.4倍标准差时监测到故障。泄漏导致压力发生阶跃偏移的监测结果如图10所示。当压力发生1倍标准差偏移时，分块MPCA的SPE统计量超出对应的控制限，成功监测到故障；全变量MPCA模型未能监测到故障。当压力偏移增大至2倍标准差时，分块和全变量模型都能准确监测到故障。由以上监测结果可见，相对于全变量MPCA模型，分块MPCA监测模型对变量的微小波动更加敏感，可以更早发现故障。

(a)分块MPCA模型

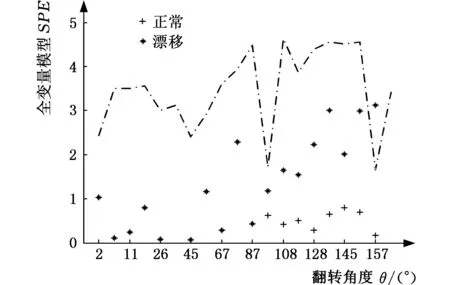
(b)全变量MPCA模型图9 分块与全变量MPCA模型对压力漂移性泄漏的SPE统计量Fig.9 The SPE of multi-blocks and all variables MPCA model for pressure drifting leakage

4 结论

(1)本文建立了C80型翻车机液压系统卸料过程的物理模型和统计模型，并用两种模型对其工作过程进行故障监测。结果表明，基于物理模型的故障监测方法受到模型精度的影响较大，而统计建模仅需要正常工作状态下的监测数据就可以建立相对准确的模型，适应于物理建模精度较低的生产过程故障监测。

(2)提出根据液压系统工作机理对各阶段的监测变量进行分块，再由每个块中的变量分别建立子MPCA模型。将基于全部变量的MPCA模型与分块MPCA模型应用于翻车机保压阶段液压缸泄漏故障的监测。结果证明分块MPCA模型可以监测到泄漏导致压力偏移量最小为0.9倍标准差的故障，而全变量的MPCA模型仅可以监测到偏移量最小为1.4倍标准差的泄漏。翻车机液压在线监测与诊断系统6个月的运行情况表明，相对于全变量的MPCA模型，分块MPCA模型可以使故障的识别率由80%提高到95%，从而为港口物料的正常运输提供了有力保障。

(a)分块MPCA模型

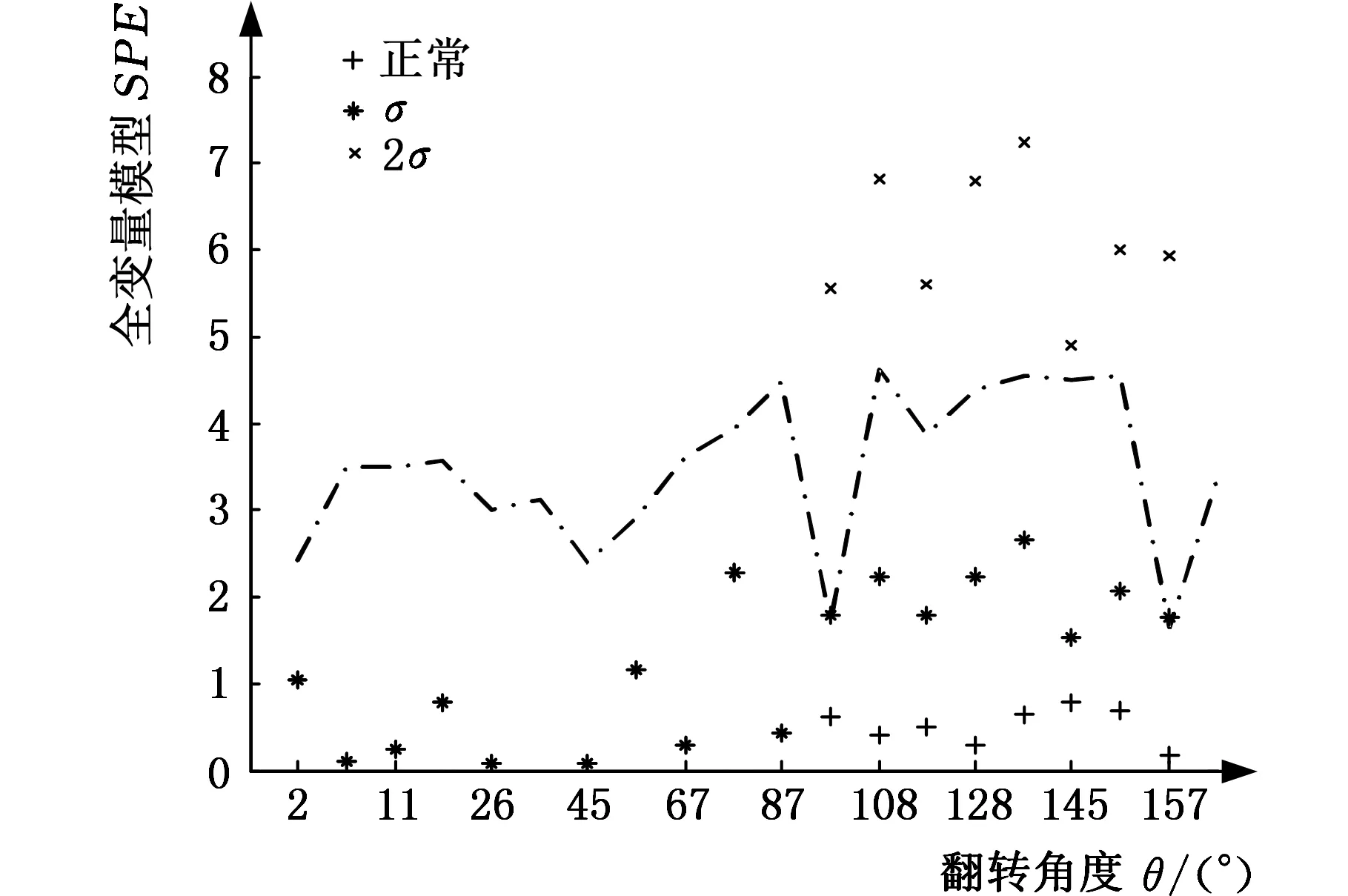
(b)全变量MPCA模型图10 分块与全变量MPCA模型对压力偏移性泄漏的SPE统计量Fig.10 The SPE of multi-blocks and all variables MPCA model for pressure bias leakage

参考文献：

[1] KU W, STORER R H, GEORGAKIS C. Disturbance Detection and Isolation by Dynamic Principal Component Analysis[J]. Chemometrics and Intelligent Laboratory Systems, 1995, 30: 179-196.

[2] 朱荷蕾，孟婥，孙以泽，等. 基于分段线性MPCA的充液氨过程建模及监控[J]. 仪器仪表学报，2015, 36(2): 271-279.

ZHU Helei, MENG Zhuo, SUN Yize, et al. Modeling and Monitoring of Ammonia Reactor Filling Process Based on Piecewise Linear MPCA Method[J]. Chinese Journal of Scientific Instrument, 2015, 36(2): 271-279.

[3] 齐咏生，王普，高学金，等. 一种新的多阶段间歇过程在线监测策略[J]. 仪器仪表学报，2011,32(6): 1290-1297.

QI Yongsheng, WANG Pu, GAO Xuejin, et al. Novel Online Monitoring Strategy for Multiphase Batch Processes[J]. Chinese Journal of Scientific Instrument, 2011,32(6): 1290-1297.

[4] 许仙珍，谢磊，王树青. 基于PCA混合模型的多工况过程监控[J]. 化工学报，2011, 62(3): 743-752.

XU Xianzhen, XIE Lei, WANG Shuqing. Multi-mode Process Monitoring Method Based on PCA Mixture Model[J]. CIESC Journal, 2011, 62(3): 743-752.

[5] 周奇才，黄克，赵炯，等. 基于改进型滑动窗主元分析的盾构液压系统故障诊断研究[J]. 中国机械工程，2013, 24(5) : 638-643.

ZHOU Qicai, HUANG Ke, ZHAO Jiong, et al. Research on Fault Diagnosis of Hydraulic System for Shield Machine Based on Improved Moving Windows Algorithm of Principal Component Analysis[J]. China Mechanical Engineering, 2013, 24(5) : 638-643.

[6] NOMIKOS P, MACGREGOR J F. Monitoring Batch Processes Using Multiway Principal Component Analysis[J]. Aiche Journal, 1994, 40(8):1361-1375.

[7] 钱学清，张惠侨. 斗轮卸料的过程及理论建模[J]. 机械设计与研究，1994，3 : 21-23.

QIAN Xueqing, ZHANG Huiqiao. Theoretical Modeling of Bucket Wheel Unloading Process[J]. Machine Design and Research, 1994, 3 : 21-23.

[8] 宋正阳. 散体煤岩自然安息角相似模拟试验研究[J]. 煤炭技术，2015，34(6) : 47-50.

SONG Zhengyang. Similar Simulation Experiment on Natural Repose Angle of Granular Rock[J]. Coal Technology, 2015, 34(6) : 47-50.

[9] 陆宁云，王福利，高福荣，等. 间歇过程的统计建模与在线监测[J]. 自动化学报，2006, 32(3): 401-410.

LU Ningyun, WANG Fuli, GAO Furong, et al. Statistical Modeling and Online Monitoring for Batch Process[J]. Acta Automatica Sinica, 2006,32(3): 401-410.

[10] JACKSON J E, MUDHOLKAR G S. Control Procedures for Residuals Associated with Principal Component Analysis[J]. Technometrics, 2012, 21(3):341-349.