非磁性微粒的负磁泳-惯性组合分选研究

杜加友 郭望城 王瑞金 朱泽飞,

1.浙江理工大学机械与自动控制学院,杭州,3100182.杭州电子科技大学机械工程学院,杭州,310018

0 引言

利用微通道分选悬浮在液体中的非磁性颗粒(如细胞)，在肿瘤学、干细胞研究和基因测序等领域有着很好的应用前景[1-2]。惯性微流经常用于细胞(或粒子)根据大小的分选，如将血液中的白细胞、红细胞和血小板进行分离。虽然惯性微流可以通过收缩-扩展通道[3-5]或弯曲通道[6-9]来提高分离效率，然而如果要分离尺寸非常接近的颗粒(如正常细胞与变异细胞的大小差距就很小)，仅依靠惯性效应来分离是很困难的。因此，人们开始探索各种方法来加大颗粒在微通道中的侧向迁移，进而产生了声泳[10]、热泳[11]、介电泳[12]、光泳[13]等颗粒分离方法。

磁泳是指黏性介质中的磁性颗粒在受到外加磁场作用下的运动。磁泳分离是磁性颗粒受到磁场力诱导，产生定向移动，从而实现颗粒分离的方法，在生物医药和化学分析中得到了广泛应用[14-17]。然而，非磁性颗粒的分选无法直接利用磁场力，所以大多采用颗粒先与磁珠结合后再用磁场力进行分离的方法[18]，这样就必须预先对被分离颗粒进行磁珠标记。还有一种方法则是利用负磁泳(negative magnetophoresis)来进行分离[19-20]。负磁泳是指非磁性/抗磁性颗粒在黏性液体中受磁场力作用，产生与磁场梯度方向相反的磁浮力，从而推动颗粒远离磁源的运动[21]。值得注意的是，产生负磁泳的先决条件是颗粒的导磁率必须比载流液体(前述的黏性液体)低，这时磁浮力的大小不但与磁场的梯度有关，还与载流液体和非磁性颗粒的磁化强度有关，当然还与颗粒的直径有关[22-24]。负磁泳分离的最大优势是无需对目标颗粒进行修饰和标记，而且可以通过改变载流液体的磁化强度来调节，因为载流液体一般采用磁性液体(或称磁流体)，这种磁流体是把粒径为几纳米到几十纳米的磁性颗粒稳定地分散在载液中形成的胶体[25]。这种液体的性能在无外磁场的作用下几乎与载液相同，在外磁场作用下则产生磁化，磁化的强度与纳米磁性颗粒浓度相关，所以可以通过纳米磁性颗粒大小或浓度来调节磁流体的磁化强度[26]。

近年来，非磁性颗粒的负磁泳分离的研究报道逐渐增多，其中最多的是反磁性颗粒在负磁泳作用下的运动，如文献[26-27]验证了被动惯性聚束和主动磁迁移相结合的反磁性颗粒的分离方法，建立了三维数值模型，并以此研究聚苯乙烯颗粒在不同颗粒尺寸、不同MnCl2浓度、不同流动速度下，在矩形微通道中产生的侧向偏移[28]。HEJAZIAN等[29]研究了磁场强度、鞘流率和颗粒颗粒尺寸不同时，反磁性颗粒在非均匀磁场作用下的迁移，但是以上文献针对的是抗磁性颗粒。对于无磁性的颗粒在负磁泳作用下的运动研究，FATEEN等[30]建立了包括磁场、流场和颗粒运动方程的有限元计算模型，模拟了磁泳分离；KUMAR等[31]设计了一个将惯性分离和磁分离相结合的微分离器件，通过综合考虑流速比和磁场强度的组合，可以高效分离多种尺寸的颗粒，但无法对颗粒直径非常接近的颗粒进行分离；CHENG等[32]建立了非磁性颗粒在磁流体中输运的三维分析模型，并研究了不同流率、磁流体性质和几何参数下颗粒运动轨迹[33]；YAN等[34]设计了一个磁泳辅助的水泳颗粒聚集器，研究了流率、颗粒尺寸、导磁率和磁场强度对聚集效率的影响；DAS等[35]研究了将磁水动力学和磁泳相结合的颗粒输运机制，计算了颗粒运动轨迹。然而，以上文献没有从非磁性颗粒在非均匀磁场中的受力出发，探寻以磁泳力为主的非磁性颗粒惯性分选规律。

笔者为分离颗粒直径十分接近的无磁性颗粒，提出了将无磁性颗粒的负磁泳运动和颗粒的惯性迁移相结合的方法，并在此基础上设计具有通道收缩-扩张结构的负磁泳耦合的惯性分选器，最后分析和讨论外磁场强度、流动速度比、结构参数等对分选精度和效率的影响。

1 组合分选器的设计

1.1 负磁泳原理

磁泳是指在磁场诱导作用下磁性颗粒在流体内的定向移动，颗粒此时受到的磁泳力指向磁场强度增大的方向。负磁泳是指在磁场诱导作用下，非磁性或抗磁性颗粒在流体中产生与磁场梯度相反的一种运动[19]。磁泳力具体表达式为[36]

Fm=μ0Vp[(Mp-Mf)·]H

(1)

式中，Mp、Mf分别为颗粒和流体的磁化强度；Vp为颗粒体积；H为磁场强度；μ0为真空磁导率。

式(1)对磁性颗粒的磁泳运动和非磁性颗粒的负磁泳运动都适用。显然，磁泳力的大小和方向不仅与磁场梯度大小和颗粒体积有关，还与颗粒和流体的磁化强度有关。颗粒的磁化强度大于流体的磁化强度时，磁泳力的方向与磁场梯度方向相同；颗粒的磁化强度小于流体的磁化强度时，磁泳力的方向与磁场梯度方向相反，此时即为负磁泳。图1所示为磁泳分离原理，图1c、图1e为负磁泳，而图1b中，对于颗粒p2(见图中标注)来说是负磁泳。另外，由式(1)还可以知道，不同磁化强度的颗粒即使大小相同,也能利用磁泳进行分离；磁化强度相同的颗粒，也可以根据其大小进行分离。因此，根据尺寸对非磁性颗粒进行磁泳分离时，一般会采用磁化强度比较高的磁流体，常用的磁流体有盐溶液和纳米磁流体，纳米磁流体是将10 nm左右的磁性纳米颗粒均匀分布在载液里形成的胶体。

(a)Mp1≥Mp2≥Mf，Vp1=Vp2(b)Mp1≥Mf≥Mp2，Vp1=Vp2

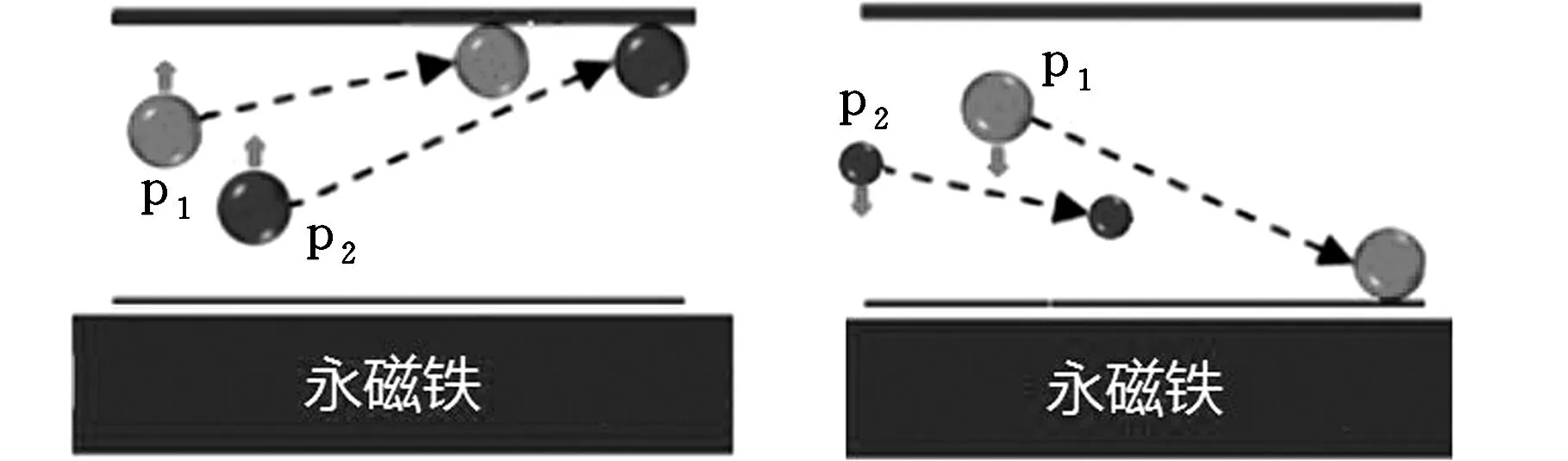
(c)Mf≥Mp2≥Mp1，Vp1=Vp2(d)Mp1=Mp1≤Mf，Vp1≥Vp2

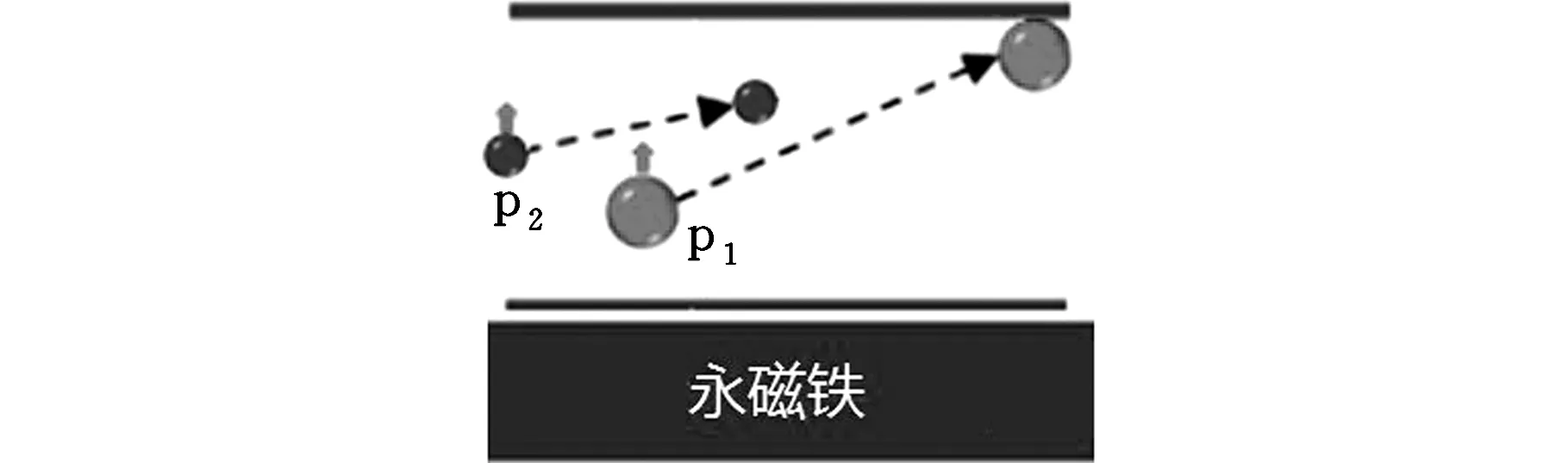
(e)Mp1=Mp2≤Mf，Vp1>Vp2图1 颗粒的磁泳分离原理图Fig.1 Schematic diagram of magnetophoresis

1.2 非磁性颗粒在磁流体中的受力分析

要让非磁性颗粒能够根据其尺寸进行分离，应当让不同尺寸的颗粒能在特定的平衡位置聚集，然后根据平衡位置的不同，把非磁性颗粒从不同出口导出，这就涉及非磁性颗粒在流体中的受力和运动。

非磁性颗粒在磁流体中的运动极为复杂，影响其受力和运动的因素有流体性质、流场分布、颗粒性质和颗粒尺寸、外磁场大小和分布等。不考虑纳米磁性颗粒之间作用和纳米颗粒对分选的非磁性颗粒(微米级)的作用，非磁性颗粒将受到流体的黏性阻力、重力与浮力、附加质量力、压力梯度力、Magnus升力、Saffman升力、Basset力、布朗力、热泳力等，根据相关文献分析可知[11]，当颗粒尺寸在1～10 μm时，重力加浮力、压强梯度力、附加质量力差不多在同一数量级，但与磁场力相比，至少小三个数量级，因此可以忽略不计，况且大多数生物流体中的颗粒密度与溶液的差距不大，所以重力与浮力几乎抵消。另外Magnus升力、Saffman升力比黏性阻力小2～3个数量级，也几乎可以忽略。在不考虑温度不均匀、外界没有大扰动时，可以不考虑Basset力和热泳力。当然，布朗力是随机力，对颗粒定向移动影响很小，也可以不考虑。总之，当颗粒尺寸在1～10 μm时，需要考虑的主要是磁场力和黏性力。

由于流体的黏性效应，当颗粒的运动速度大于其周围流体速度时，颗粒会受到流体的阻力；反之，颗粒就会受到流体的拖曳力，根据斯托克斯公式有

FD=-6πμrp(vp-vf)fD

(2)

式中，μ为流体动力黏度；rp为颗粒半径；vp、vf分别为颗粒和流体速度；fD为阻力系数。

在斯托克斯阻力中，fD=1，如果考虑壁面附近的颗粒，则需要对fD进行修正：

(3)

其中，e为颗粒与通道壁之间的距离。显然，离壁面越远，阻力系数越大。

1.3 分选器设计

首先以惯性分选器为基础，利用微通道的结构变化产生多个微腔，每个腔内都会产生一个微涡，使大尺寸的颗粒容易产生跨流线迁移[3-5]。通道的收缩与扩展使流线产生弯曲，从而产生迪恩涡，有利于颗粒的分选，见图2。

(a)微通道结构

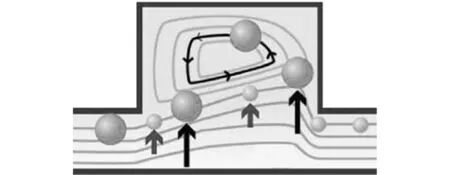
(b)微涡作用

(c)迪恩涡作用图2 惯性微流颗粒分选原理Fig.2 Mechanism of inertial sorting

其次，为了进一步放大颗粒侧向偏移的距离，在微通道的微腔下面设置永磁体，将颗粒的负磁泳运动叠加到惯性迁移运动中。

最后，为了顺利将聚焦在不同平衡位置、不同尺寸的非磁性颗粒从不同的出口导出，将微通道的宽度放大，因为这样能将平衡位置之间的距离拉大。

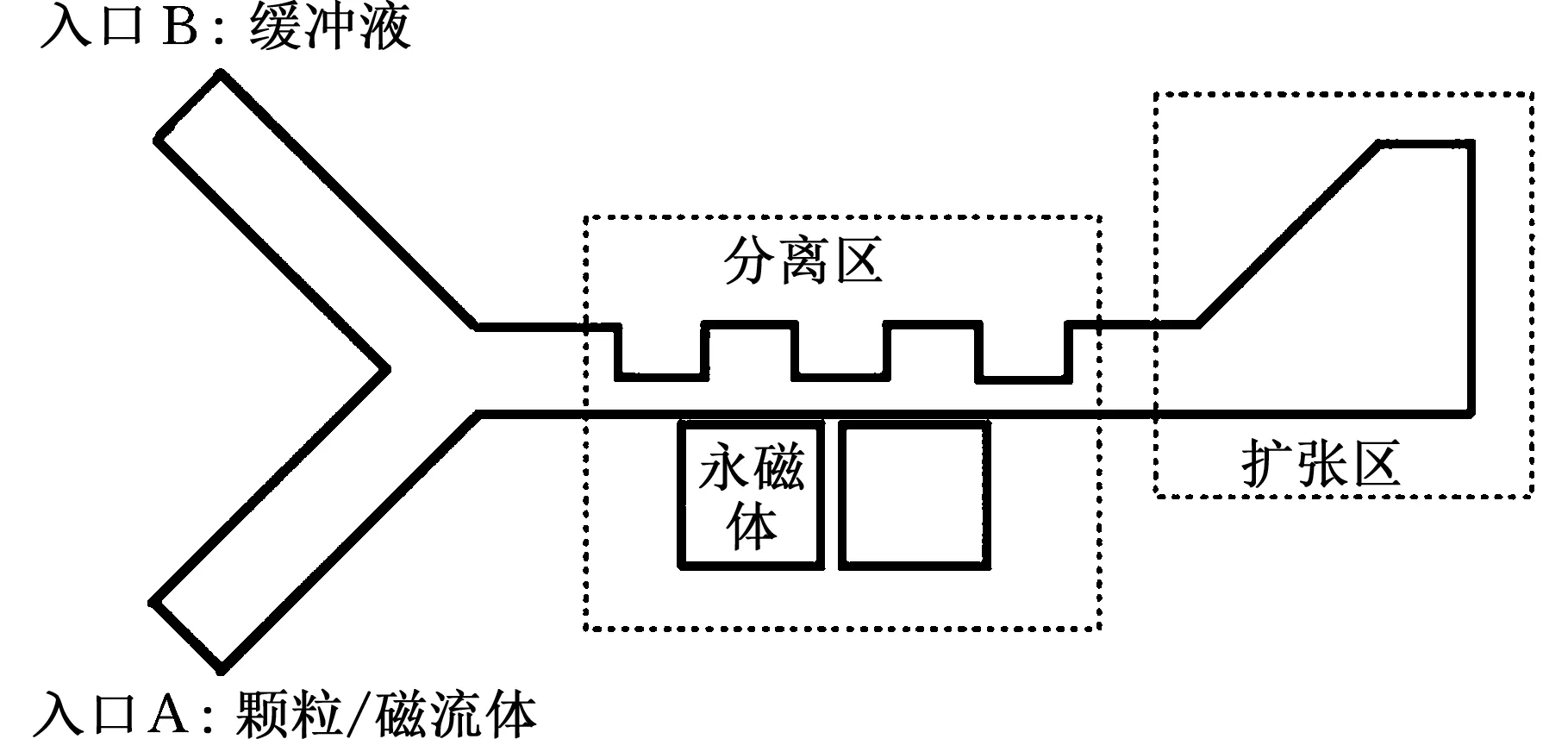
(a)结构示意图

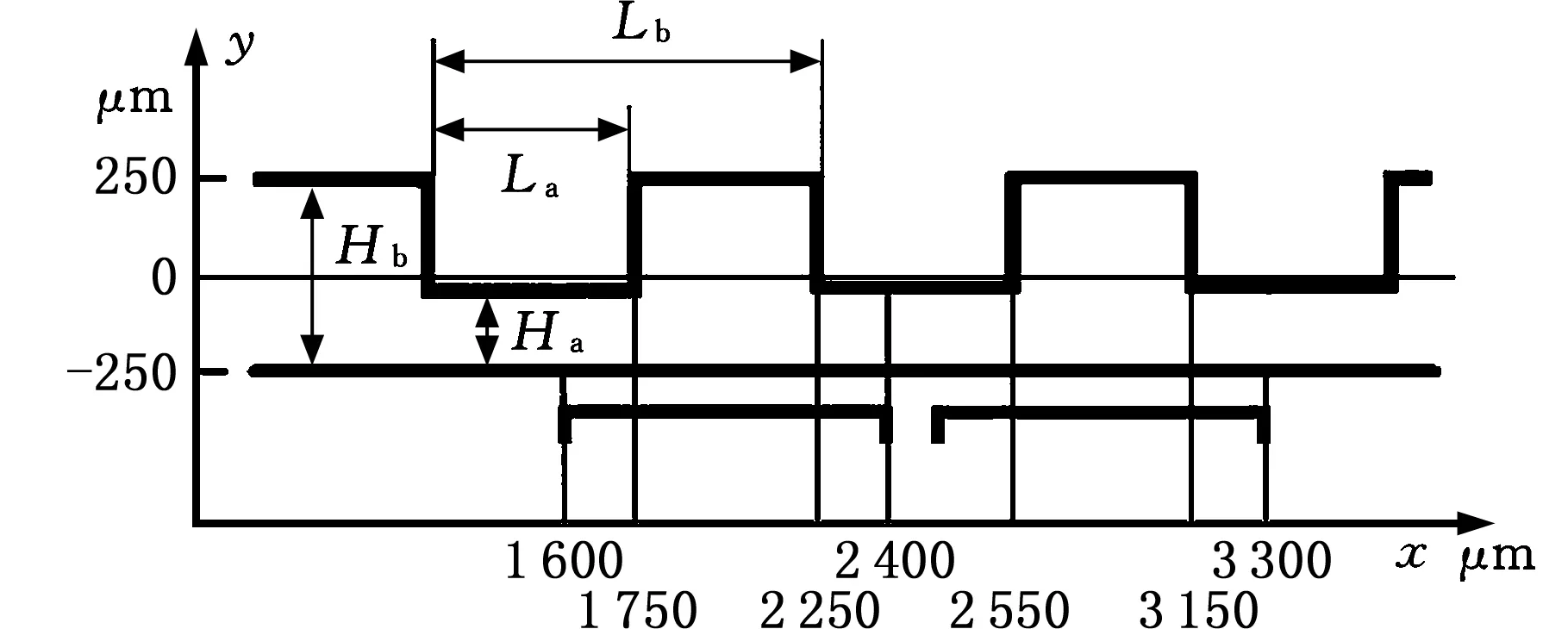
(b)结构尺寸示意图图3 负磁泳耦合惯性非磁性颗粒分选器图Fig.3 Negative-coupled inertial sorter for non-magnetic particle

在以上三个方面的分析基础上，设计了图3所示的负磁泳耦合非磁性颗粒惯性分选器。由图3可见：负磁泳耦合的非磁性颗粒惯性分选器可以分成3个区域：入口区、分离区和扩张区。入口A导入需要分离的颗粒和缓冲液，入口B导入缓冲液。研究中，缓冲液采用体积分数为1%的Fe3O4纳米磁性流体。分离区在直通道上设置了3个通道收缩区，以利于颗粒的惯性分选；在下壁面附近设有永磁体，以在收缩-扩展通道区产生非均匀磁场，从而将负磁泳分选和惯性分选进行耦合。扩张区的设置是让不同尺寸的颗粒分布带之间的距离放大，以便将不同尺寸的颗粒从不同的出口导出。

2 数值计算模型的建立

为验证图3结构设计的合理性，探索不同因素对颗粒分选的影响规律，采用数值模拟的方法对磁场的分布、流体的流动以及颗粒的运动进行计算，为此首先需要建立数值计算模型。负磁泳耦合的非磁性颗粒惯性分选器的数值计算模型包含流场计算、磁场计算和颗粒轨迹计算三个模型。

2.1 流场计算模型

在不考虑外界温度变化情况下，微通道内流场计算方程组由质量守恒方程和动量守恒方程组成。定常流动质量守恒方程为

·vf=0

(4)

由于微通道尺寸小，雷诺数范围一般为10-3～102。由于微通道内流动液体的平均自由程很小，所以努森数在N-S方程适用的范围内，因此动量守恒方程可以写为

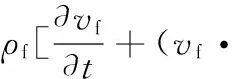
(5)

式中，ρf为流体密度；p为压力；F为源项，主要考虑磁场力。

磁性纳米流体的黏度随纳米颗粒浓度、环境温度、外磁场强度等变化而变化[37]，对于非磁性颗粒分选来说，磁流体的颗粒浓度固定，环境温度的变化也可以忽略，因此只要考虑外磁场的变化对磁流体黏度的影响即可。文献[37-38]研究表明，对体积分数为1%的纳米颗粒磁流体而言，磁场强度从0增加到8×105A/m时，黏度增加不超过20%，而且对于这种颗粒体积分数较小的情况，黏度随外场的增加基本上是线性的(图4)，这里用磁流体黏度与基液黏度之比(简称黏度比)来衡量磁流体黏度与磁场的关系。但是，随纳米颗粒体积分数的增大，黏度就越来越偏离线性关系，如图4中纳米颗粒体积分数为6%的情况。根据文献[37-38]的研究数据可以得到小纳米颗粒体积分数的磁流体黏度比的线性拟合计算式：

μ/μb=[1+2.5φ+(1.2φ+0.31φ2)H/26.8]

(6)

其中，μb为纳米流体基液的黏度；φ为纳米颗粒体积分数。

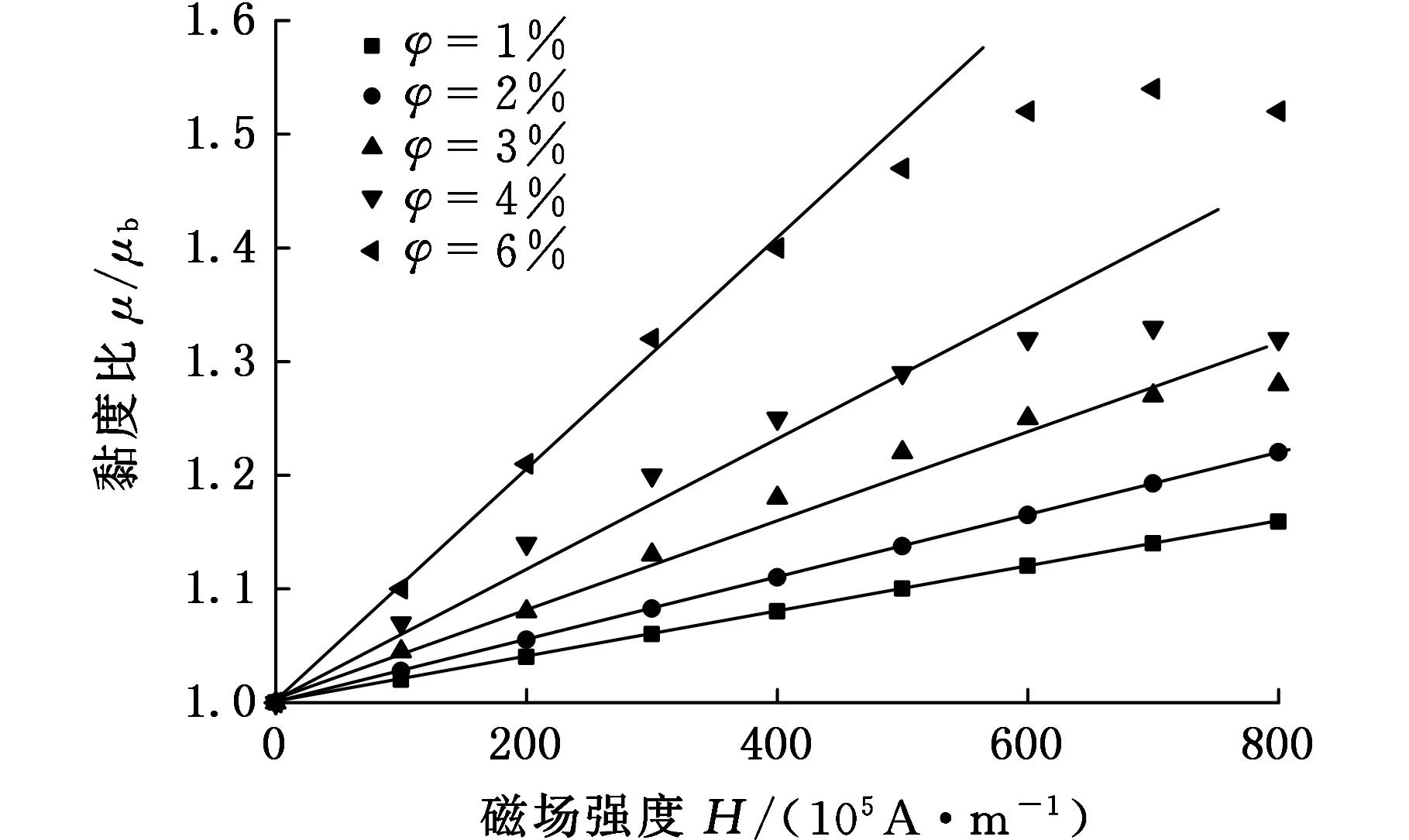
图4 磁流体黏度比-磁场强度的关系Fig.4 Viscosity ratio of magnetic fluid with vs magnetic field intensity

2.2 磁场计算

由于动量守恒方程(式(5))中的源项只考虑磁场力，所以源项即为磁场力。为了能够根据式(1)计算颗粒所受的磁浮力，需要计算微通道内的磁场强度和流体的磁感应强度，根据Maxwell方程组有[39]

×H=0

(7)

·B=0

(8)

B=μ0(Mf+H)

(9)

式中，B为磁感应强度；Mf为磁流体的磁化强度。

由于非磁性颗粒是稀相，所以不考虑其对纳米流体磁化的影响。磁流体磁化强度的计算相当复杂，磁流体磁化强度可以通过郎之万函数来表示和计算[40]：

Mf=αarctan(βH)

(10)

其中，α、β为图5所示的磁流体磁化曲线的参数。

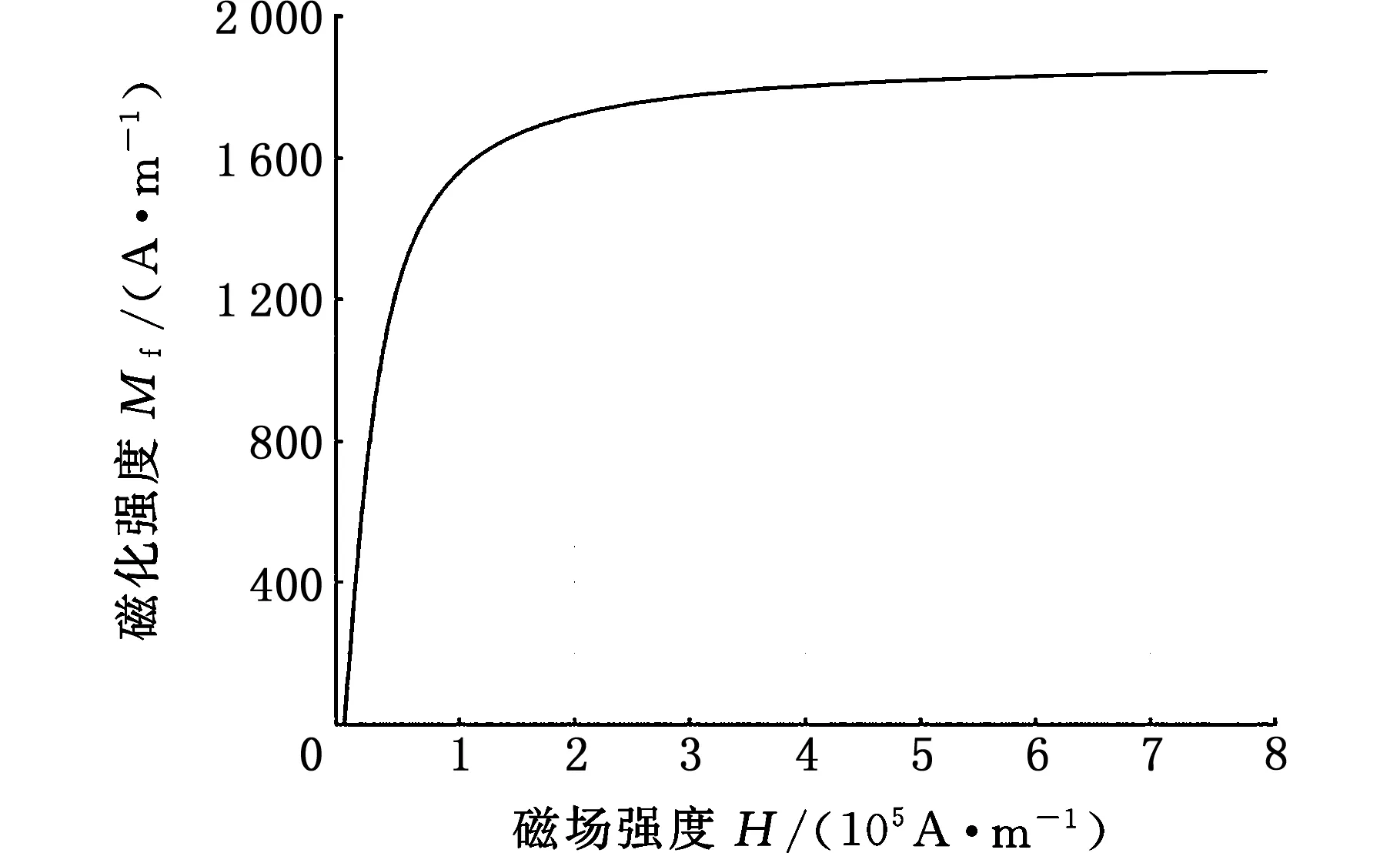
图5 磁流体磁化曲线Fig.5 Magnetizing curve of magnetic fluid

2.3 颗粒轨迹计算

根据1.2节的分析可知，非磁性颗粒在磁流体中的受力主要考虑磁浮力和黏性阻力，根据牛顿第二定律有

(11)

式中，mp、Fm、FD分别为颗粒质量、磁力和黏性力。

根据式(11)可以求得颗粒的运动轨迹。由于分选颗粒迁移速度变化不是很剧烈，而且磁流体的流动速度波动也不大，所以忽略式(11)的惯性项并代入式(2)，可以得到非磁性颗粒的运动方程：

(12)

(13)

式中，vp,x、vp,y分别为非磁性颗粒在主流方向(x向)和侧向(y向)的速度分量；vf,x、vf,y分别为磁性液体在主流方向和侧向的速度分量；Hx、Hy、Mx、My分别为磁场强度和磁化强度在主流方向和侧向的分量。

2.4 试算与验证

在试算前设置好条件与参数，具体见表1。

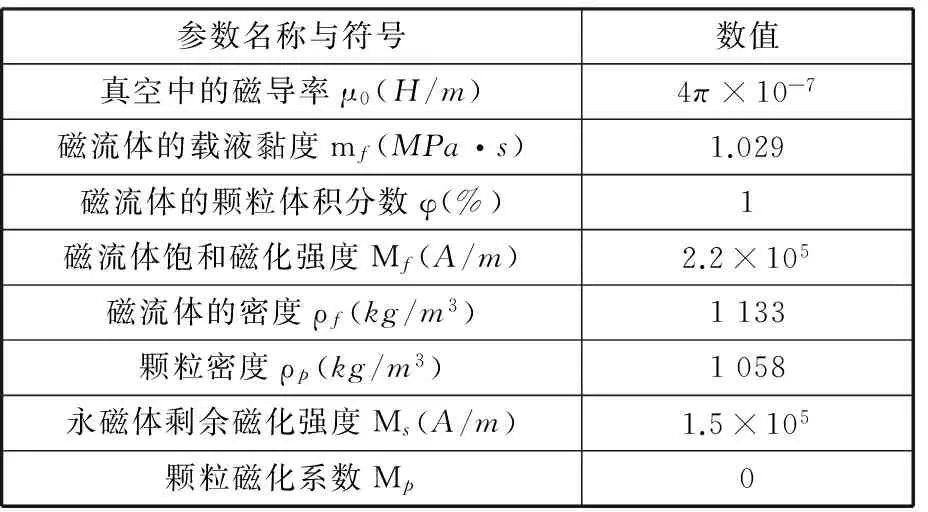
表1 计算参数

2.4.1磁场计算

为了简化计算，我们针对直通道边放置2个方形永磁体的例子进行计算(图6)。在网格划分时，永磁体和通道壁面附近需要细化，否则磁场梯度和磁浮力的曲线就会不光滑。为了获得较高的磁场梯度，采用基泰尔畴[41]，根据式(7)～式(10)，可以用有限元计算2个永磁体产生的叠加磁场。由图6a可见，微通道内2个永磁体交界处有比较强的磁场，当然磁通密度最大处还是在永磁体内部。由图6b可见，沿主流方向2～2.5 mm处的磁场强度最高，而且磁场梯度也有最大值，由此验证了采用基泰尔畴可以得到高的磁场梯度。

(a)磁通密度云图

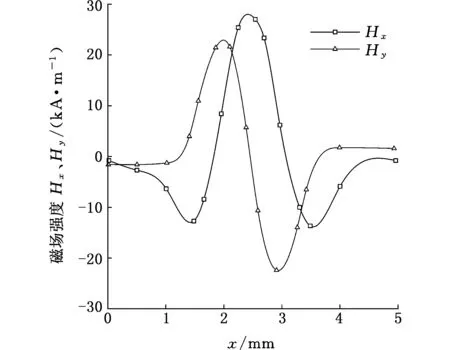
(b)沿坐标x方向的磁场强度分布图6 直通道磁场计算Fig.6 Calculation for magnetic field in straight channel

2.4.2流场计算

用流体力学方程(式(4)～式(6))可以计算微通道内的流场，需要注意的是, 计算时先要根据磁场分布计算不同位置的磁流体的黏度，然后才能进行流体力学方程的迭代计算。计算结果见图7。磁场的作用使通道内的磁流体的黏度发生变化，因此对微通道内的流动产生扰动，使流线产生波动。中间的波浪线是速度最大点连成的曲线，其实质就是最中间的一条流线。此外，通道内抛物线速度剖面受磁场的影响产生了扭曲，形成了不对称形状。

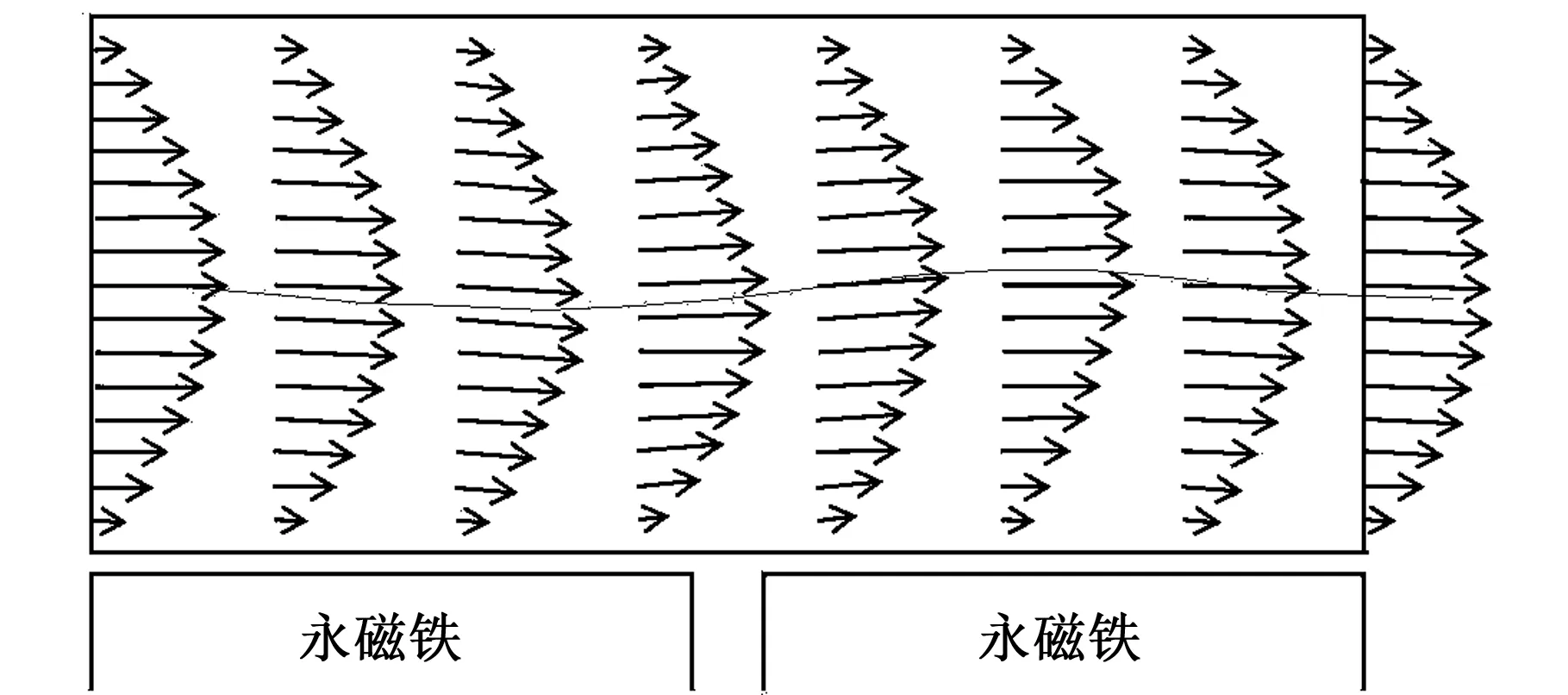
图7 微通道内流场(速度剖面分布)Fig.7 Flow field in microchannel(velocity profile)

2.4.3颗粒轨迹计算

为了验证磁场对非磁性颗粒运动的影响，根据式(12)计算颗粒直径dp为2 μm、5 μm的两种非磁性颗粒在外磁场作用下的受力和运动。图8所示为直径为2 μm、5 μm颗粒从入口A中心释放时的受力。可以看到，5 μm颗粒的侧向受力Fy2明显比2 μm颗粒的侧向受力Fy1要大，这与式(1)的预测一致；另一个非常重要的特点是，侧向受力Fy明显大于主流方向的受力Fx，有利于颗粒产生侧向迁移。图9所示为直径5 μm颗粒在入口A的不同位置释放时的侧向磁场力Fy，y=-150 μm处释放的颗粒受到的侧向磁场力明显比其他地方释放的颗粒大，这正是颗粒需要从入口A释放的原因，只有这样颗粒才能在微通道内靠近永磁体的区域通过，使颗粒受到比较大的侧向磁场力Fy，从而产生更大的侧向迁移。

图8 中心位置2 μm、5 μm颗粒的受力Fig.8 Magnetic forces on the particles of 2 μm,5 μm Released at channel center

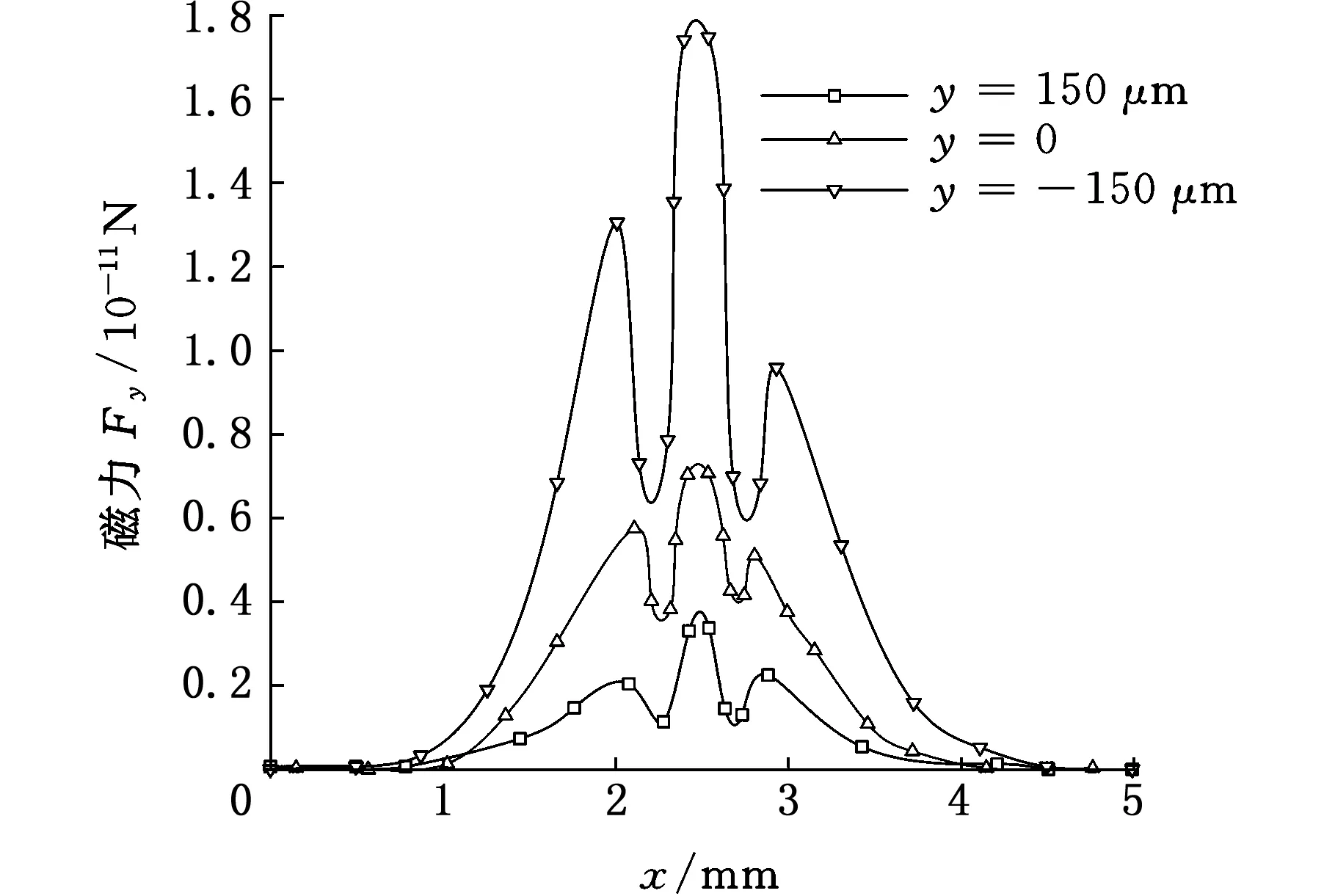
图9 不同位置5 μm颗粒的受力Fig.9 Magnetic forces on the particles of 5 μm Released at other position

图10所示为2 μm和5 μm颗粒的侧向迁移情况，由于2 μm的颗粒(小颗粒)磁场力相对较小，所以随流性较好，侧向偏移较小；5 μm的颗粒(大颗粒)磁场力相对较大，所以侧向偏移也大，由此可见，不同大小的非磁性颗粒是可以在磁场作用下分选的。

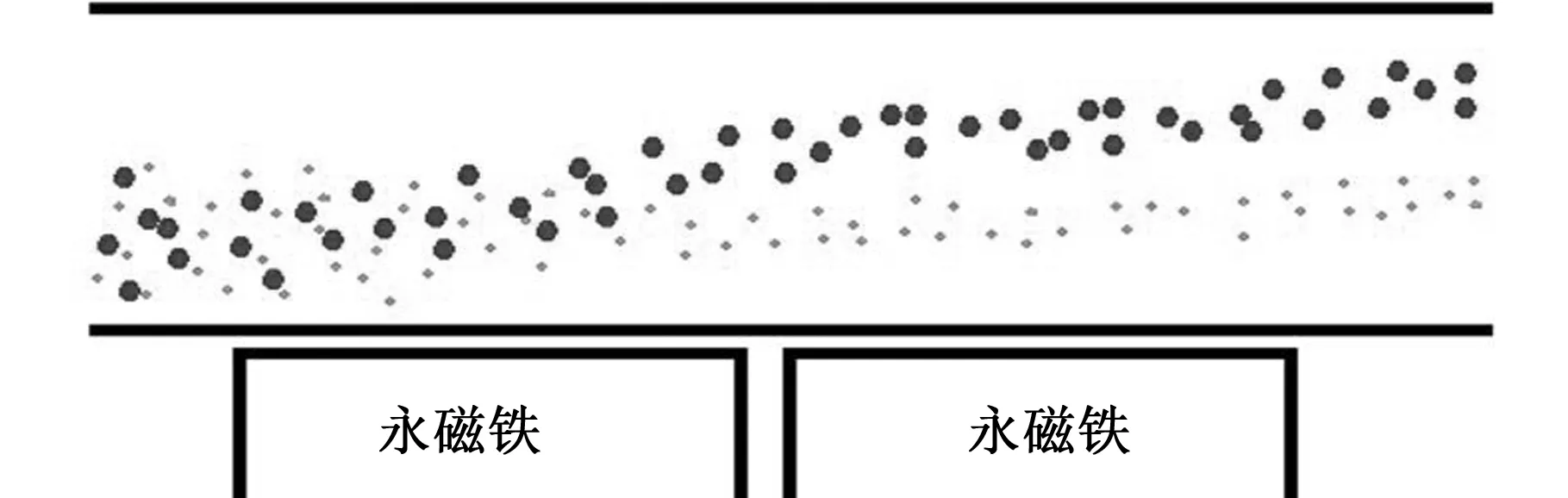
图10 2 μm、5 μm颗粒的运动轨迹Fig.10 Trajectory of particle with a diameter of 2 μm,5 μm

3 负磁泳-水动力耦合分选规律

3.1 入口流速对分离效率的影响

颗粒分选主要关注分选效率——出口目标颗粒总数与入口目标颗粒总数的比值。一般说来，只有分离效率80%以上的颗粒分离才有应用价值。

入口流速会对颗粒分选效率产生影响，在两个入口流速范围均在1～10 mm/s时，对粒径为3 μm、4 μm和5 μm非磁性颗粒的运动轨迹进行计算。图11所示为不同粒径、不同入口流速下非磁性颗粒的分离效率，可见：同一粒径颗粒的分离效率随入口流速的减小而明显升高。流速越小，颗粒停留在磁场作用区域的时间越长，颗粒受到磁场力作用的时间也越长，产生的侧向偏移就越大，也就提高了分离效率。对于不同直径的颗粒来说，在同一流速下，大粒径的颗粒分离效率高，因为颗粒所受磁力的大小与粒径的三次方成正比，而黏性力在速度相同的情况下，与粒径正比，综合考虑以上二个方面因素得到，颗粒受力随颗粒直径增大而增大。

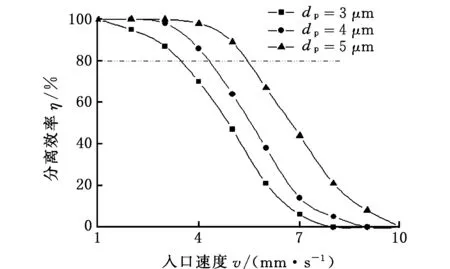
图11 入口流速对分离效率的影响Fig.11 Effect of inlet velocity on separation efficiency

3.2 入口流速比对分离效率的影响

为了提高分离效率，在颗粒分离技术中经常使用鞘流[42-43]。颗粒在管道初始位置存在较大的分散性，而鞘流能减小这种分散性，即压缩颗粒分布带宽，因此在磁泳分离中也可以使用该技术[44]。由于受到鞘流的限制，非磁性颗粒分布带在进入分离通道时不再是在通道宽度方向上均匀分布，而是聚焦在微通道靠近永磁体的一侧。颗粒分布带的带宽取决于鞘流速度vB(入口B)与样品液流速vA(入口A)的比值(流速比)，比值越大，颗粒分布带宽就越小。因此，可以通过改变2个入口的流速比来调节颗粒分布带宽，提高颗粒的分离效率。为了保证有比较高的分离速度，在微通道2个入口速度满足“入口B流速与入口A流速之和为8 mm/s”条件下，改变A、B两个入口流速，得到不同的流速比，计算经过分离区后颗粒分布的带宽(表2)。由表2可见，流速比越大，颗粒分布带宽越小，有利于颗粒分离。图9表明，颗粒越靠近永磁体一侧，受到的侧向迁移的磁浮力Fy越大，越有利于加大颗粒的侧向迁移，与表2的结果是一致的。

表2 不同流速比下的颗粒束宽度

图12所示为不同入口流速比下3 μm、5 μm非磁性颗粒在离开分离区(x=4.5 mm处)时颗粒分布带宽，图中长线段代表5 μm微粒在离开分离区时的分布带，而短线段则代表3 μm的微粒带宽。从图12可见，随着B入口与A入口流速比的增大，重叠区域逐渐减小。当流速比达到4时，两种颗粒离开分离区时的带宽重叠已完全消失；随着比值的继续增大，两种颗粒分布带之间的距离增大，颗粒带宽逐渐减小，实现颗粒的100%分离。

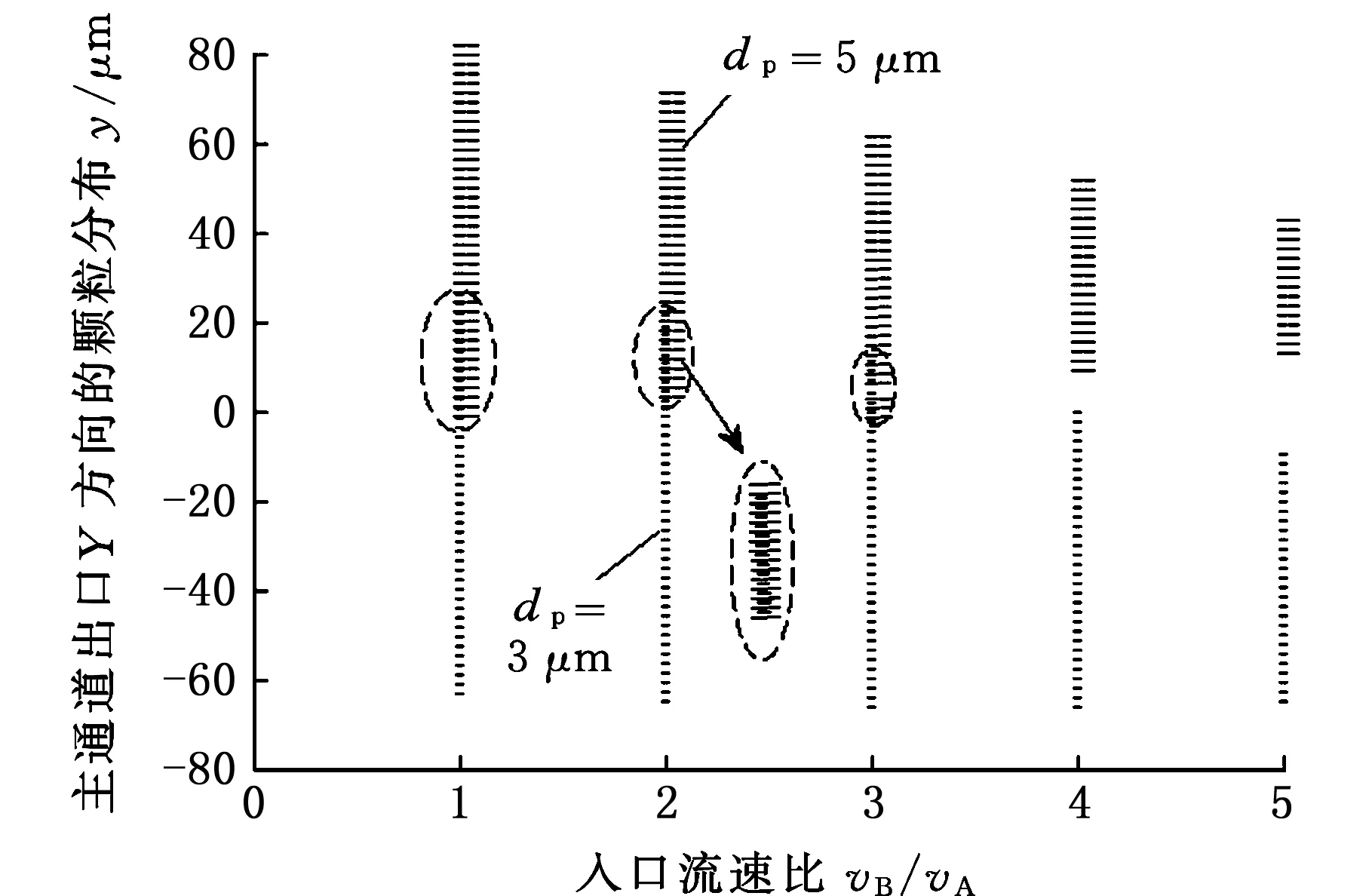
图12 不同入口流速比时的两种颗粒带宽的位置Fig.12 Locations of particle band at various inlet velocity

3.3 磁场强度的影响

根据前面的分析可知，非磁性颗粒在磁性液体中的平衡位置是由磁力和黏性力共同作用决定的。磁力的大小与非磁性颗粒的侧向迁移距离直接相关，因此数值模拟了不同磁场强度(0.19～0.38T)下，粒径分别为3 μm、4 μm、5 μm的非磁性颗粒运动轨迹，计算了颗粒平均的迁移距离(图13)，其中，入口B流速为8 mm/s，入口A流速为4 mm/s，流速比为2。由图13可知，颗粒的侧向迁移距离随磁场强度的增大而增大，但是迁移距离的增量对不同粒径的颗粒是不同的，颗粒直径越大，侧向迁移距离的增量越大，这正是负磁泳能对不同尺寸非磁性颗粒进行有效分离的依据。

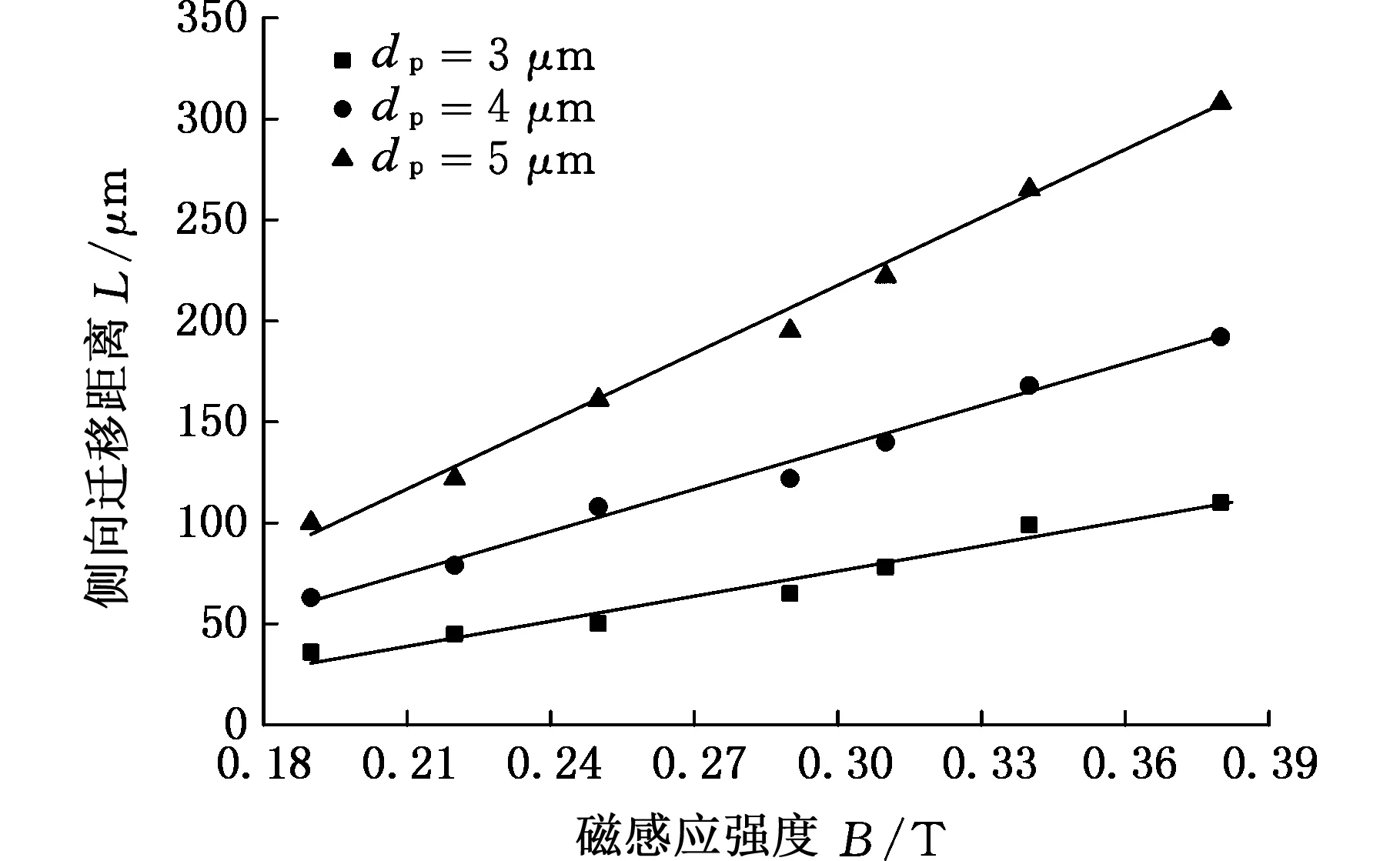
图13 磁场强度对颗粒侧向迁移距离的影响Fig.13 Effect of magnetic field on lateral migration distance

3.4 微通道结构的影响

微通道结构在惯性微流中能促使颗粒的跨流线迁移，但是结合磁场力作用的惯性分离规律还不甚清晰，为了研究负磁泳-惯性耦合颗粒分离中的水动力因素对颗粒分离的影响，对不同扩张-收缩比(Ha/Hb=2/5，1/2，3/5)的情况进行了数值模拟，计算2 μm、5 μm颗粒的平均侧向迁移距离差，计算中固定La=500 μm，Lb=1 000 μm。Ha、Hb、La、Lb含义见图3b。需要解释的是，两种颗粒的平均侧向迁移距离差越大，效率越高。

由图14可见，Ha/Hb越小，两种颗粒迁移距离差越大，越容易分离，因为Ha/Hb越小，样品液的带宽越小，样品分布带越靠近永磁体，受到的磁力越大，侧向迁移距离也越大；另外，磁场强度越大，颗粒侧向迁移距离差越大，而且近似于线性关系。

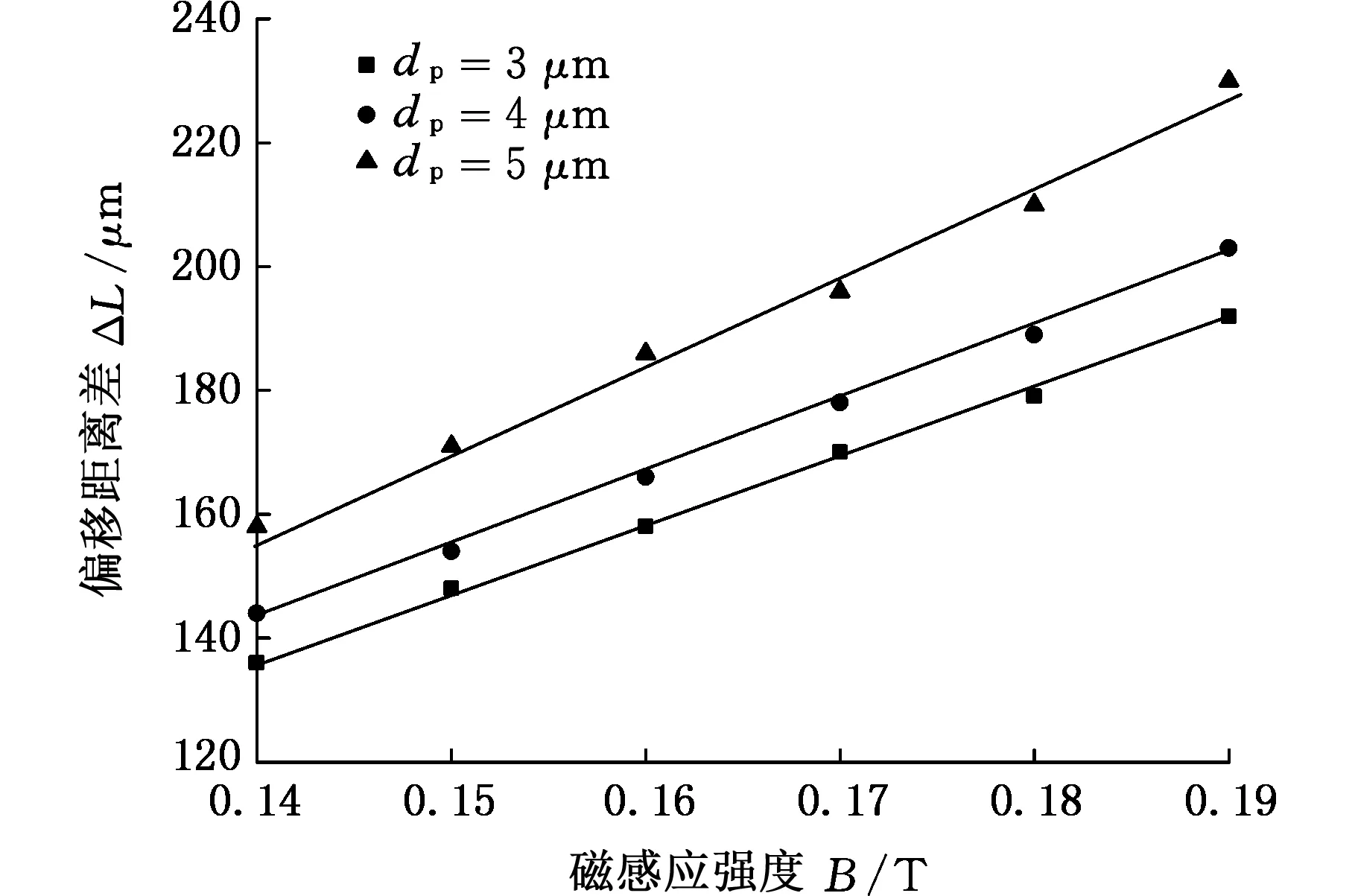
图14 不同微通道结构下的颗粒偏移Fig.14 Particle migration in various microchannel

由图15可见，颗粒直径小时，其侧向迁移距离也小，颗粒分布带经常聚焦在通道的下半部分；颗粒直径越大，侧向迁移距离越大，颗粒分布带会逐渐过渡到上半部分，而且越来越往上，有利于大小颗粒的分离。在颗粒分选器中希望被分离的两种颗粒分别聚焦在上下部分，所以图15就能为设计颗粒分选器提供指导。直径2 μm、5 μm的两种颗粒容易分离，这是因为颗粒分布带之间的距离较大(200 μm左右)。分离直径2 μm、3 μm颗粒的难度就很大，因为颗粒分布带都聚焦在下半部分，颗粒分布带之间的距离较小(50 μm左右)。当然，如果要分离多种颗粒，相互之间的侧向偏移和颗粒分布带之间的距离差要足够大。此外，Ha/Hb对小颗粒的侧向迁移影响不大，但随着颗粒直径的增大，不同Ha/Hb曲线之间的间距逐渐变大，Ha/Hb的作用就显现出来了。

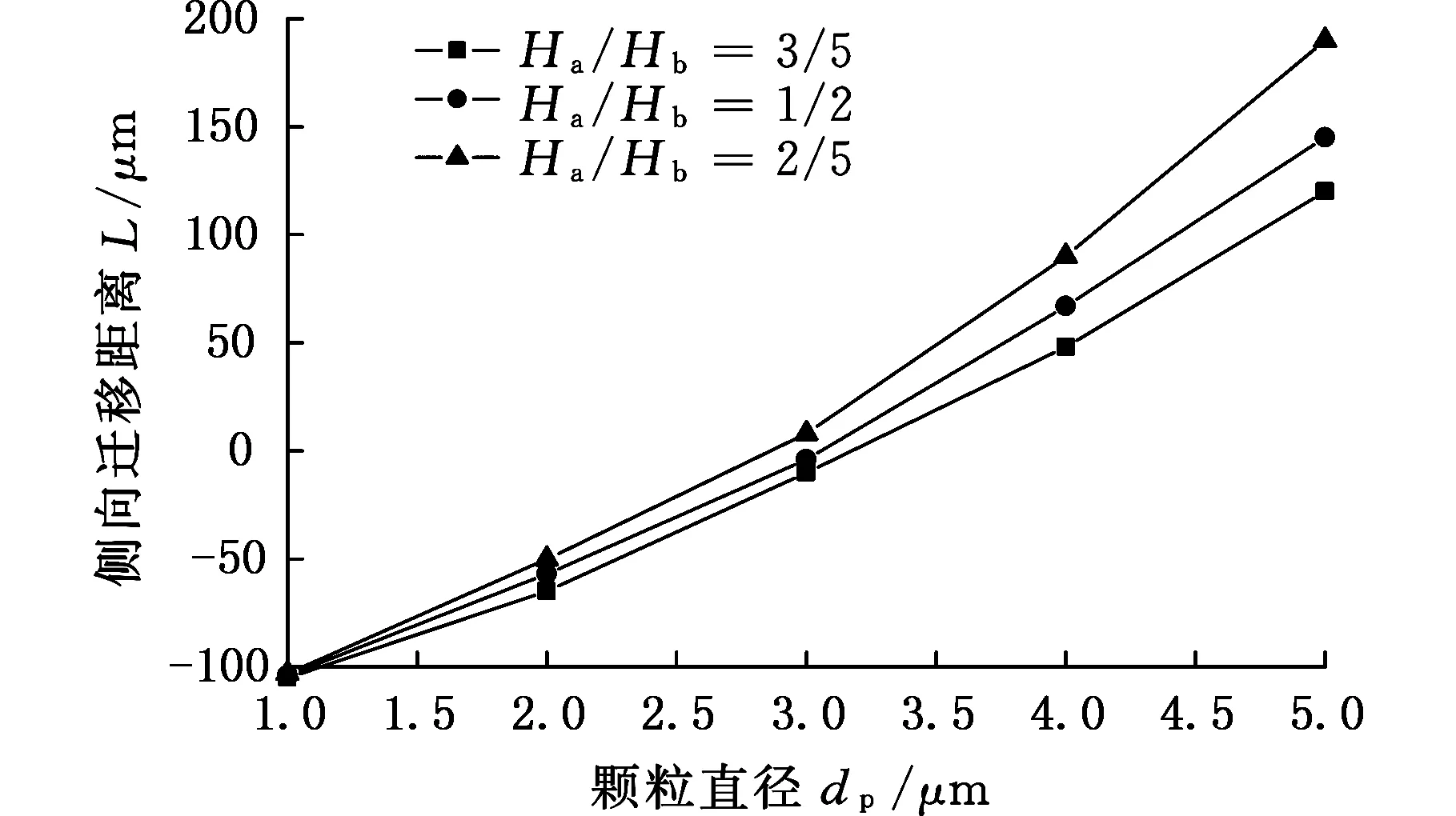
图15 不同颗粒直径的侧向迁移距离Fig.15 Lateral migration distance of various particles

3.5 扩张区的影响

众所周知，颗粒分布带宽越小、不同颗粒分布带宽间距越大，颗粒分选效率就越高。为了说明扩张区对颗粒分选的影响，在通道扩张收缩比Ha/Hb=3/5，流速比vA/vB=1/2，扩张区扩张比为1/3，永磁体最大磁通密度为0.18 T的情况下，在入口A均匀释放粒径分别为3 μm、4 μm、5 μm的颗粒,其运动轨迹见图16。由图16可见，扩张区在增加各种颗粒分布带宽的同时，也明显增加了带宽之间的距离，这有利于不同颗粒从不同出口导出。表3为扩张前后不同粒径颗粒分布，3 μm、4 μm颗粒之间带宽间距从71 μm放大到217 μm，而4 μm、5 μm颗粒之间带宽间距从27 μm放大到102 μm，二者均放大3倍有余。

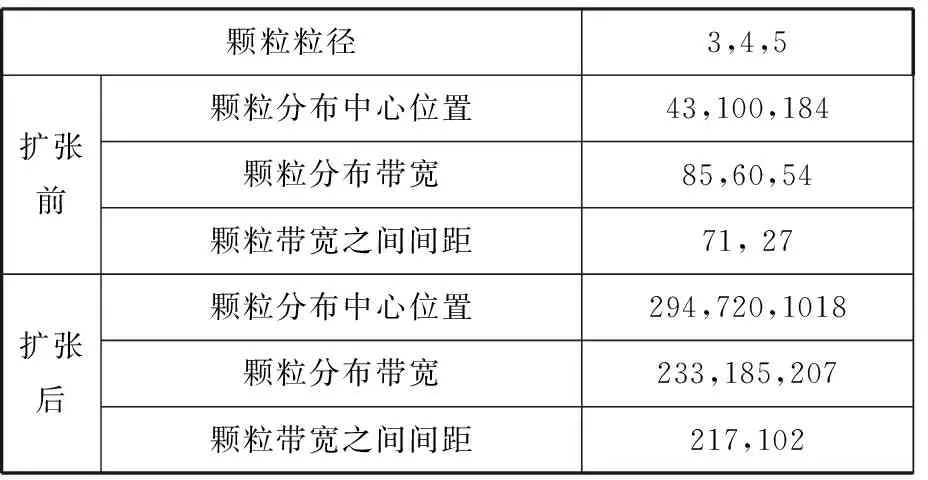
表3 颗粒带比较

3.5 实验验证

为了验证数值模拟结果，用溶胶-凝胶法制得3种Fe3O4亚微米磁性颗粒(见图17)，透射电子显微镜(TitanTMG2 60-300)测得平均粒径为765 nm、988 nm、1 235 nm，然后进行荧光包裹，得到平均粒径2 880 nm、3 775 nm、5 085 nm的颗粒(Microtrac S3500)。用振动样品磁强计(VSM-350)测量其磁化强度分别为28×103A/m、12×103A/m、0，与体积分数1%的磁流体磁化强度相比可以忽略，颗粒基本上可以认为是非磁性的。

最后用激光诱导荧光图像法获得荧光图像，实验装置包含激光器及其电源、微泵微芯片等微流组件、高速CCD与图像处理组件、显微镜组件等(图18)，高速CCD拍摄得到5个部位的荧光粒子图像(图16 Ⅰ～Ⅴ)，5个位置的图像清晰显示了不同尺寸颗粒的分离过程，而且还可以利用图16中位置Ⅴ的图像，计算出颗粒带宽和带宽之间距离的平均值(表4)，以此来验证数值模拟结果。此外，由图16位置图像Ⅰ～Ⅴ看出，经过Ⅱ、Ⅲ两个位置后，不同粒径颗粒之间的距离逐渐增大，说明磁场作用对颗粒分离的贡献较大，同时，对比位置Ⅳ、Ⅴ可以看出，扩张区的设置能明显加大不同尺寸颗粒带之间的距离，有利于颗粒分离和导出。

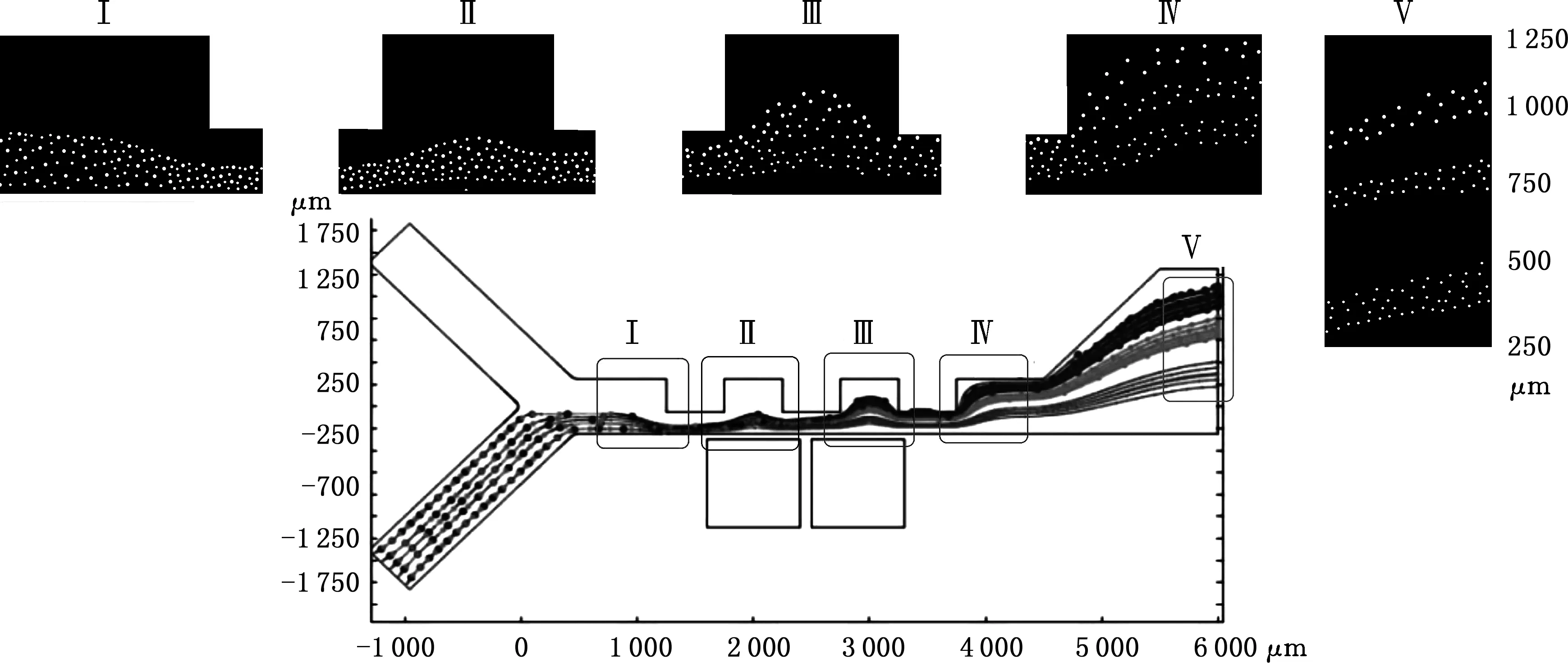
图16 入口均匀释放的三种颗粒的运动轨迹以及试验图像(流速比1∶2，永磁体最大磁通密度为0.18T)Fig.16 Trajectory and LIF images of three kinds of particles(Inlet velocity ratio 1∶2, magnetic flux density 0.18T)

图17 Fe3O4亚微米磁性颗粒的TEM图像Fig.17 TEM image of Fe3O4 submicroparticle

图18 激光诱导荧光图像实验装置Fig.18 Experimental setup for laser induced fluorescence

颗粒粒径345颗粒分布中心模拟结果2947201018实验结果3657671068

4 结论

(1)外加磁场不但会对微通道内磁流体的流动产生影响，也会对微通道内非磁性颗粒运动产生明显影响。非磁性颗粒的侧向迁移距离随磁场强度的增大而增大，随非磁性颗粒尺寸增大而增大。

(2)同一粒径颗粒的分离效率随入口流速的减小而明显提升，因为增加了颗粒在磁场作用区域的停留时间，延长了磁场力作用的时间，产生了更大的侧向位移，从而提升了分离效率。

(3)颗粒越接近永磁体一侧，受到的侧向迁移的磁浮力越大，从而有利于加大颗粒侧向迁移距离，因此流速比增大，颗粒分布带就更接近永磁体，有利于颗粒分选效率的提高。

(4)微通道结构参数Ha/Hb越小，两种颗粒迁移距离差越大，越容易分离，因为Ha/Hb越小，样品液的带宽越小，样品带越靠近永磁体，受到的磁力就越大，侧向迁移距离越大。此外，Ha/Hb对小颗粒的侧向迁移影响不大，但随着颗粒直径的增大，对应不同Ha/Hb的曲线之间的间隙逐渐变大，Ha/Hb的作用就越来越显著。

(5)扩张区明显增加了带宽之间的距离，虽然也增加了各种颗粒分布带宽，但总体上有利于不同颗粒从不同出口导出，实现分离。

参考文献：

[1] DANOVA M, TORCHIO M, MAZZINI G. Isolation of Rare Circulating Tumor Cells in Cancer Patients: Technical Aspects and Clinical Implications[J]. Expert Review of Molecular Diagnostics, 2011, 11(5): 473-485.

[2] JO K, CHEN Y L, PABLO J J, et al. Elongation and Migration of Single DNA Molecules in Microchannels Using Oscillatory Shear Flows[J]. Lab on a Chip, 2009, 9(16):2348-2355.

[3] LEE M G, CHOI S, PARK J K. Inertial Separation in a Contraction-expansion Array Microchannel[J]. Journal of Chromatography A, 2011, 1218(27): 4138-4143.

[4] TSAI C H, LIN C H, FU L M, et al. High Performance Microfluidic Rectifier Based on Sudden Expansion Channel with Embedded Block Structure[J]. Biomicrofluidics, 2012, 6(2): 241068-241089.

[5] WANG R J. Hydrodynamic Trapping of Particles in an Expansion-contraction Microfluidic Device[J]. Abstract and Applied Analysis, 2013, 2013: 496243.

[6] DI C D, IRIMIA D, TOMPKINS R G, et al. Continuous Inertial Focusing, Ordering and Separation of Particles in Microchannels[J]. Proceedings of the National Academy of Science, 2007,104(48):18892-18897.

[7] MARTEL J M, TONER M. Inertial Focusing Dynamics in Spiral Microchannels[J]. Physics of Fluids, 2012, 24(3): 032001.

[8] XIANG N, CHEN K, DAI Q, et al. Inertia-induced Focusing Dynamics of Microparticles throughout a Curved Microfluidic Channel[J]. Microfluidics and Nanofluidics, 2015,18(1):29-39.

[9] ZHANG J, LI W, LI M, et al. Particle Inertial Focusing and Its Mechanism in a Serpentine Microchannel[J]. Microfluidics and Nanofluidics, 2014, 17(2):305-316.

[10] OBERTI S, NEILD A, QUACH R D, et al. The Use of Acoustic Radiation Forces to Position Particles within Fluid Droplets[J]. Ultrasonics, 2009,49(1):47-52.

[11] WANG R J, DU J Y, GUO W C, et al. Investigation on the Thermophoresis-coupled Inertial Sorting of Submicrometer Particles in a Microchannel[J]. Micro-Nano-scale Thermophysical Engineering, 2016, 22(1):51-65.

[12] ZHANG C, KHOSHMANESH K, MITCHELL A, et al. Dielectrophoresis for Manipulation of Micro/Nano Particles in Microfluidic Systems[J]. Analytical and Bioanalytical Chemistry, 2010, 396(1):401-420.

[13] LI W K, SOONG C Y, TZENG P Y, et al. Analysis of Transition and Mobility of Microparticle Photo-phoresis with Slip-flow Model[J]. Microfluidics and Nanofluidics, 2011,10(1):199-209.

[14] MACIEJ Z, LEE R M, WILLIAMS P S, et al. Separations Based on Magnetophoretic Mobility[J]. Journal of Separation Science and Technology, 2002, 37(16): 3611-3633.

[15] PAMME N, WILHELM C. Continuous Sorting of Magnetic Cells via On-chip Free-flow Magnetophoresis[J]. Lab Chip, 2006, 6(8):974-980.

[16] 吴信宇,吴慧英,胡定华.基于磁力场与速度场协同的高效微通道磁泳分离[J].中国科学: 科学技术, 2011, 41(12): 1620-1627.

WU Xinyu, WU Huiying, HU Dinghua. High-efficiency Magnetophoretic Separation Based on Synergy of Magnetic Force Field and Flow Field in Microchannels[J]. Science China : Technological Sciences, 2011,41(12): 1620-1627.

[17] 杜晶辉,刘旭,徐小平.微流控芯片分选富集循环肿瘤细胞的研究进展[J]. 色谱 , 2014, 32(1): 7-12.

DU Jinghui, LIU Xu, XU Xiaoping. Advances in Isolation and Tumor Cells in Microfluidic Chip[J]. Chinese Jounal of Chromatography, 2014, 32(1): 7-12.

[18] THOMAS S, STEPHAN K, LEE M, et al. Sequential CD34 Cell Fractionation by Magnetophoresis in a Magnetic Dipole Flow Sorter[J]. The Analyst, 2010, 135(1): 62-70.

[19] 邓海东,李海. 磁性液体中非磁性小球与磁性纳米颗粒的相互作用及磁组装[J]. 物理学报,2013,62 (12):127501-10.

DENG Donghai, LI Hai. Interaction and Assembly of Non-magnetic and Magnetic Nanoparticles Dispersed in Magnetic Field[J]. Acta Phy. Sin., 2013, 62(12): 127501-10.

[20] MELISSA K, RANDALL M E, BENJAMIN B Y, et al. Formation of Ordered Cellular Structures in Suspension via Label-free Negative Magnetophoresis[J]. Nano Letters, 2009,9(5):1812 -1817.

[21] ROSENSWEIG R E. Ferrohydrodynamics[M]. Cambridge： Cambridge University Press, 1985.

[22] ZHU T T, MARRERO F, MAO L D. Continuous Separation of Non-magnetic Particles Inside Ferrofluids[J]. Microfluidics and Nanofluidics, 2010, 9(4/5): 1003-1009.

[23] ZHU T T, LICHLYTER D J, HAIDEKKER M A, et al. Analytical Model of Microfluidic Transport of Non-magnetic Particles in Ferrofluids under the Influence of a Permanent Magnet[J]. Microfluidics and Nanofluidics, 2011, 10 (6):1233-1245.

[24] CHENG R, ZHU T T, MAO L D. Three-dimensional and Analytical Modeling of Microfluidic Particle Transport in Magnetic Fluids[J]. Microfluidics and Nanofluidics, 2014,16(6):1143-1154.

[25] BERKOVSKY B, BASHTOVOI V. Magnetic Fluids and Applications Handbook[M]. UNESCO, Series of Learning Materials. New York: Begell House Inc.,1996.

[26] ZHOU Y L,SONG L, YU L D, et al. Inertially Focused Diamagnetic Particle Separation in Ferrofluids[J]. Microfluidics and Nanofluidics，2017, 21(1):14-23.

[27] LIANG L T, XUAN X C. Diamagnetic Particle Focusing Using Ferromicrofluidics with a Single Magnet[J]. Microfluidics and Nanofluidics，2012, 13(4): 637-643.

[28] ZENG J,CHEN C, VEDANTAM P, et al. Magnetic Concentration of Particles and Cells in Ferrofluid Flow through a Straight Microchannel Using Attracting Magnets[J]. Microfluidics and Nanofluidics, 2013, 15(1):49-55.

[29] HEJAZIAN M, NGUYEN N T. Negative Magnetophoresis in Diluted Ferrofluid Flow[J]. Lab Chip, 2015, 15(14): 2998-3005.

[30] FATEEN S K, MAGDY M. Three Dimensional Simulation of Negative-magnetophoretic Filtration of Non-magnetic Nanoparticles[J]. Chem. Eng. Res. & Des., 2015, 95(1):69-78.

[31] KUMAR V, REZAI P. Multiplex Inertio-magnetic Fractionation of Magnetic and Non-magnetic Microparticles in a Microfluidic Device[J]. Microfluidics and Nanofluidics, 2017, 21(1):83-98.

[32] CHENG R, ZHU T T, MAO L D. Three-dimensional and Analytical Modeling of Microfluidic Particle Transport in Magnetic Fluids[J]. Microfluidics and Nanofluidics, 2014, 16(4):1143-1154.

[33] ZHU T T, CHENG R, LIU Y F, et al. Combining Positive and Megative Magnetophoreses to Separate Particles of Different Magnetic Properties[J]. Microfluidics and Nanofluidics, 2014, 17(6):973-982.

[34] YAN S, ZHANG J, CHEN H Y, et al. Development of a Novel Magnetophoresis-assisted Hydrophoresis Micro-device for Rapid Particle Ordering[J]. Biomedical Microdevices, 2016, 18(54):1-9.

[35] DAS S,CHAKRABORTY S, MITRA S K. Magnetohydro-dynamics in Narrow Fluidic Channels in Presence of Spatially Non-uniform Magnetic Fields: Framework for Combined Magnetohydrodynamic and Magnetophoretic Particle Transport[J]. Microfluidics and Nanofluidics, 2012, 13(5):799-807.

[36] SHARPE S A. Magnetophoretic Cell Clarification[D]. Cambridge: Massachusetts Institute of Technology, 2004.

[37] REN Z, HAN Y, HONG R, et al. On the Viscosity of Magnetic Fluid with Low and Moderate Solid Fraction[J]. Particuology, 2008, 6(3):191-198.

[38] 李强，宣益民，王健. 磁流体黏度的实验研究[J]. 工程热物理学报，2005，26(5):859-861.

LI Qiang, XUAN Yimin, Wang Jian. Experimental Investigation on Viscosity of Magnetic Fluids[J]. Journal of Engineering Thermo-physics, 2005，26(5): 859-861.

[39] 李德才. 磁性液体理论及应用[M]. 北京:科学出版社, 2003.

LI Decai. The Theory and Applications of Magnetic Fluids[M]。 Beijing: Scientific Press,2003.

[40] 徐晨,刘桂雄,张沛强,等. 磁流体惯性传感的磁流耦合机理及流固结构[J].光学精密工程,2008, 16(5): 965-971.

XU Chen, LIU Guixiong, ZHANG Peiqiang, et al. Magnetic Fluid Coupling Mechanism of Magnetic Fluid Inertial Sensor and Its Magnetic-fluid Solid Structure[J]. Optics and Precision Engineering, 2008, 16(5): 965-971.

[41] ROTH I B. Characterization and Use of Permanent Magnets with Extremely Strong Field Gradient[D]. Oslo: University of Oslo, 2009.

[42] CHIU Y J, CHO S H, MEI Z, et al. Universally Applicable Three-dimensional Hydrodynamic Microfluidic Flow Focusing[J]. Lab Chip, 2013, 13(9): 1803-1809.

[43] HA B H, LEE K S, JUNG J H, et al. Three- dimensional Hydrodynamic Flow and Particle Focusing Using Four Vortices Dean Flow[J], Microfluidics and Nanofluidics, 2014,17(1):647-655.

[44] DANIEL R G, WESTBROOK M W, ALBERT J M, et al. Label-free Cell Separation and Sorting in Microfluidic Systems[J]. Analytical and Bioanalytical Chemistry, 2010, 397(8):3249-3267.