对2017年高考全国Ⅲ卷抛物线解答题的思考*

刘 刚 赵 毅

北京市第十二中学高中部 (100071)

2017年高考全国Ⅲ卷理科数学20题第(1)问是：已知抛物线C:y2=2x，过点(2,0)的直线l交C于A，B两点，圆M是以线段AB为直径的圆．证明：坐标原点O在圆M上．

本问实际上就是证明kOA·kOB=-1．在解答过程中出现了几个关键点：kOA·kOB为定值；定点(2,0)；点A，B，O在抛物线y2=2x上，如果把这些要素一般化，它们之间有怎样的关联性呢？经过思考与探究，得到了圆锥曲线内接三角形的一组性质．

性质1 已知ΔPAB的三个顶点均在抛物线y2=2px(p>0)上，且P(x0,y0)为定点，直线PA,PB的斜率分别记作k1,k2，直线AB的斜率记作k．

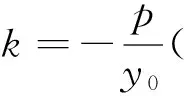
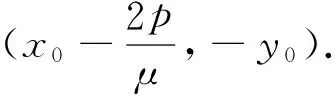
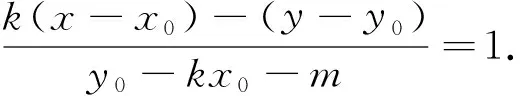
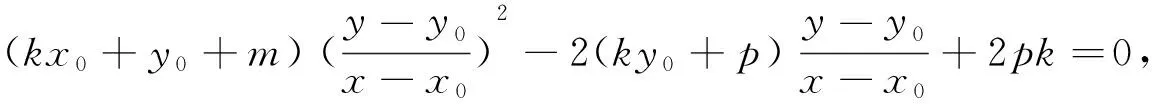
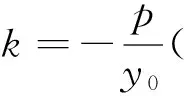
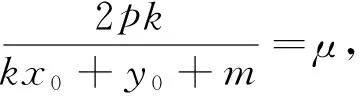
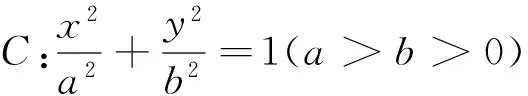
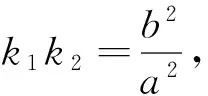
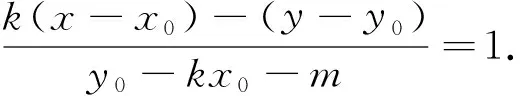
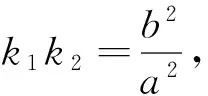
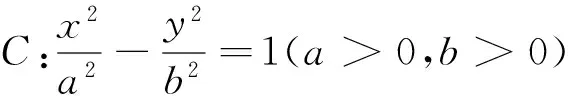
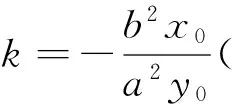
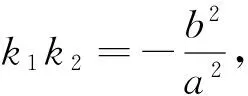
注：(1)性质3可参考性质2的证明过程，请读者自行完成；(2)这3个性质的逆命题也都成立；(3)在证明性质1，2的过程中，用到了齐次化的思想，简化了运算．