水平双向地震激励下隔震桥梁地震反应分析

张 为

（北京市市政工程设计研究总院有限公司，北京 100082）

0 引言

隔震技术具有安全、经济的优点，在桥梁结构中得到广泛的应用。在地震作用下，隔震装置为上部结构提供柔性支撑，改变结构的动力反应特性，耗散地震能量，提高结构的抗震性能。桥梁中常见的隔震支座有铅芯橡胶支座和摩擦摆支座。铅芯橡胶支座［1］（Lead Rubber Bearing， LRB）是在板式橡胶支座的中部或中心周围部位竖直压入一个或多个铅芯形成的，通过铅芯的剪切变形来实现吸收震动能量的功能。摩擦摆隔震支座（Friction Pendulum System，FPS）是一种圆弧面滑动摩擦系统［2-7］，具有较强的限位、复位能力和良好的耗能能力。

刘文光［8］、王志强［9］等对铅芯橡胶支座的耗能能力以及动力特性进行了研究，Kumar［10］和Ryan［11］提出了隔震支座的简化力学模型，Huang和Fenves［12］对铅芯橡胶支座在地震下的性能进行试验研究。Mokha［13］对大型空间网状结构的摩擦摆支座的摩擦系数和摩擦半径进行抗震分析；Hyakuda等［14］对采用摩擦摆支座的隔震体系进行仿真计算，发现计算结果和实际地震记录比较吻合。李大望［15］对摩擦摆支座的非线性特征和其隔震效果进行研究，对其在水平地震下的振动微分方程进行了推导。Ferraioli等［16］研究了铅芯橡胶支座和高阻尼橡胶支座运用于减隔震结构的抗震性能。Palazzo等［17］在研究非隔震结构与利用支座的隔震结构的随机地震反应中考虑了土对结构反应的影响，发现隔震系统在软土与硬土情况下基底位移不同。

当前研究大多只考虑了单向地震作用，本文考虑了支座的水平双向耦合作用，分析了其在双向地震作用下的力学计算模型，将简化模型应用于桥梁体系中采用数值计算的方法进行了研究，并将隔震与非隔震桥梁的地震反应进行了对比。

1 隔震支座简化计算模型

铅芯橡胶支座主要依靠金属铅的变形来消耗能量，摩擦摆支座则依靠金属之间的摩擦耗能，两者耗能机理不同。两种支座的示意图分别如图1、图2所示。

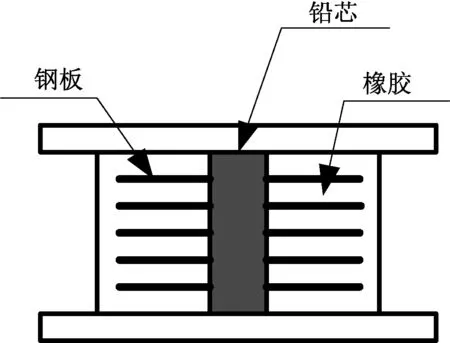
图1 铅芯橡胶支座 （LRB）Fig.1 Lead rubber bearing

图2 摩擦摆支座 （FPS）Fig.2 Friction Pendulum System

1.1 LRB计算模型

Park等［18］提出了LRB双向力 -变形关系，其示意图和计算模型图3所示，两水平正交方向的支座恢复力可用下列关系式表示：

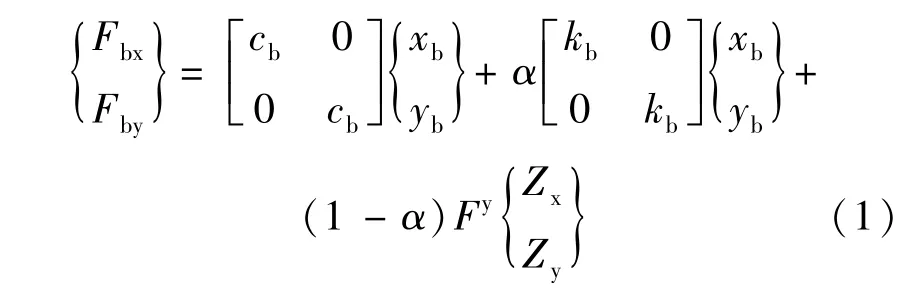
式中，Fbx和Fby分别表示支座x方向和y方向的恢复力；Zx和Zy分别表示恢复力的滞后位移分量；cb和kb分别表示支座的粘滞阻尼和初始刚度；xb和yb分别表示支座x方向和y方向相应位移；α表示支座屈服后与屈服前刚度比；Fy表示支座的屈服力。

滞后位移分量Zx和Zy满足下列耦合的非线性微分方程：

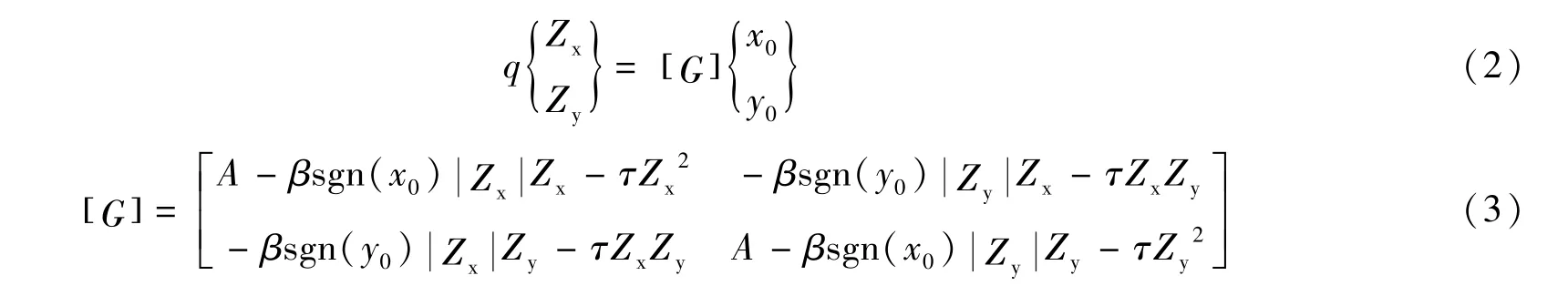
式中，β，τ和A是控制支座滞后环形状和大小的参数；x0和y0分别表示支座x方向和y方向相应初始位移；q是支座的屈服位移；sgn表示符号函数。对于LRB滞回环，各参数的取值为，q＝2.5 cm，β＝τ＝0.5，A ＝1。

根据LRB屈服后刚度，隔震周期Tb和规范化屈服力F0可由公式（4）来确定。

式中，md为桥梁上部结构的质量，∑k为LRB总的水平刚度，∑Fy示支座总的屈服力，Wd为桥梁上部结构的重量。

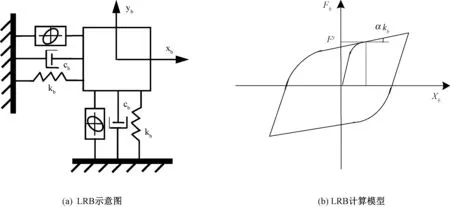
图3 LRB示意图和计算模型Fig.3 The schematic map and theoretical model of LRB

1.2 FPS计算模型

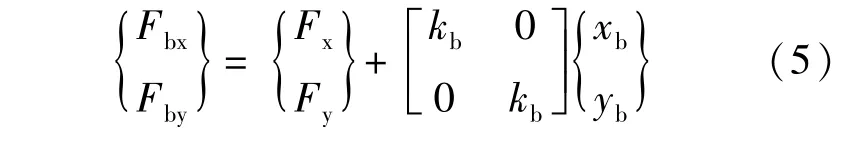
FPS的计算模型由Constantinou MC提出，示意图和计算模型图4所示，两水平正交方向的支座恢复力可用下列关系式表示［4-5］：式中，Fx和Fy分别表示支座x方向和y方向的摩擦力；kb表示在FPS曲率提供的支座刚度，kb＝Wd／R，Wd为作用在FPS支座上桥面重量，R为FPS的球面半径；xb和yb分别表示支座x方向和y方向相应位移。

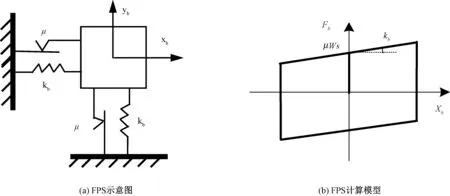
图4 FPS示意图和计算模型Fig.4 The schematic map and theoretical model of FRS

FPS在滑动前，其摩擦力的限值Fs表示为：

式中，μ为摩擦系数。

在滑动过程中，FPS的摩擦力耗散地震能量。根据摩擦力的大小，FPS的运动可分解为非滑动和滑动两个阶段。在非滑动阶段，即xb＝yb＝0，在滑动系统作用面产生的滑动摩擦力小于限制摩擦力，即＜Fs。当摩擦力达到限制摩擦力，支座系统开始滑动，即xb≠yb≠0。如果满足公式（7），FPS就会发生滑动。

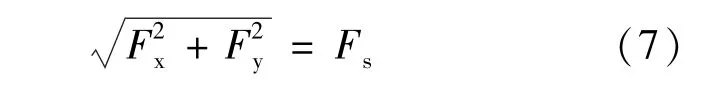
公式（7）表示FPS的作用面摩擦力为图形相互作用面。由于摩擦力的相互作用，在滑动阶段，FPS支座支承的桥梁两水平正交方向的运动方程是耦合的。

2 桥梁结构计算模型

目前，对隔震桥梁体系进行地震反应分析时，多是基于顺桥向地震动输入来计算桥梁的地震反应。而实际上地震作用是多向的，分析多向地震作用下隔震桥梁体系的地震反应时，必须考虑隔震支座水平双向相互耦合作用的力学模型，以便精确计算多向水平地震作用下桥梁的非线性地震反应。

本文以水平双向地震激励为例进行分析，隔震桥梁体系地震反应分析中一般采用的几个假设如下：

（1）在地震动计算过程中，隔震桥梁上部结构和桥墩保持弹性、无损伤。

（2）隔震桥梁的桥面是直的，在顺桥向由桥墩支撑，对规则或对称桥梁结构，扭转反应可忽略。

（3）桥台假定为刚性的，桥墩假定刚性固结在基础上，桥梁建造在坚硬的土壤或岩石上时不考虑土-结相互作用。

（4）桥梁的上部结构和下部结构离散为集中质量模型，每个节点有两个自由度，并假定每一单元的质量以点质量的形式分布在相邻节点上。

（5）只考虑桥梁的顺桥向和横桥向两个方向的地震动作用，不考虑竖向地震作用。

以三跨连续桥梁为例进行分析，隔震桥梁结构的示意图和计算模型如图5所示。在水平双向地震力作用下，隔震桥梁系统的动力方程可表述为下列矩阵形式：

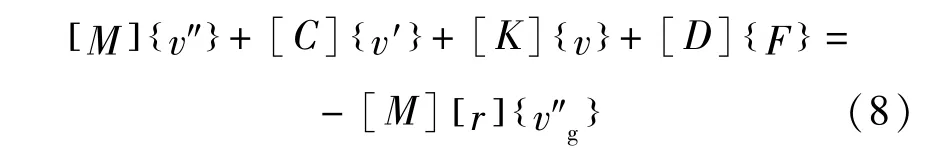
式中，［M］，［C］，［K］分别代表2N ×2N 阶桥梁结构质量，阻尼，刚度矩阵； {v″}， {v′}，{v} 分别代表结构的加速度，速度和位移向量；[D]代表LRB恢复力的局部矩阵；{F}是LRB的恢复力向量；[r]是矩阵影响系数，为单位列向量；是地震加速度向量；分别代表纵向和横向地震地面加速度；xi，yi分别代表桥梁第i节点纵向和横向的位移。

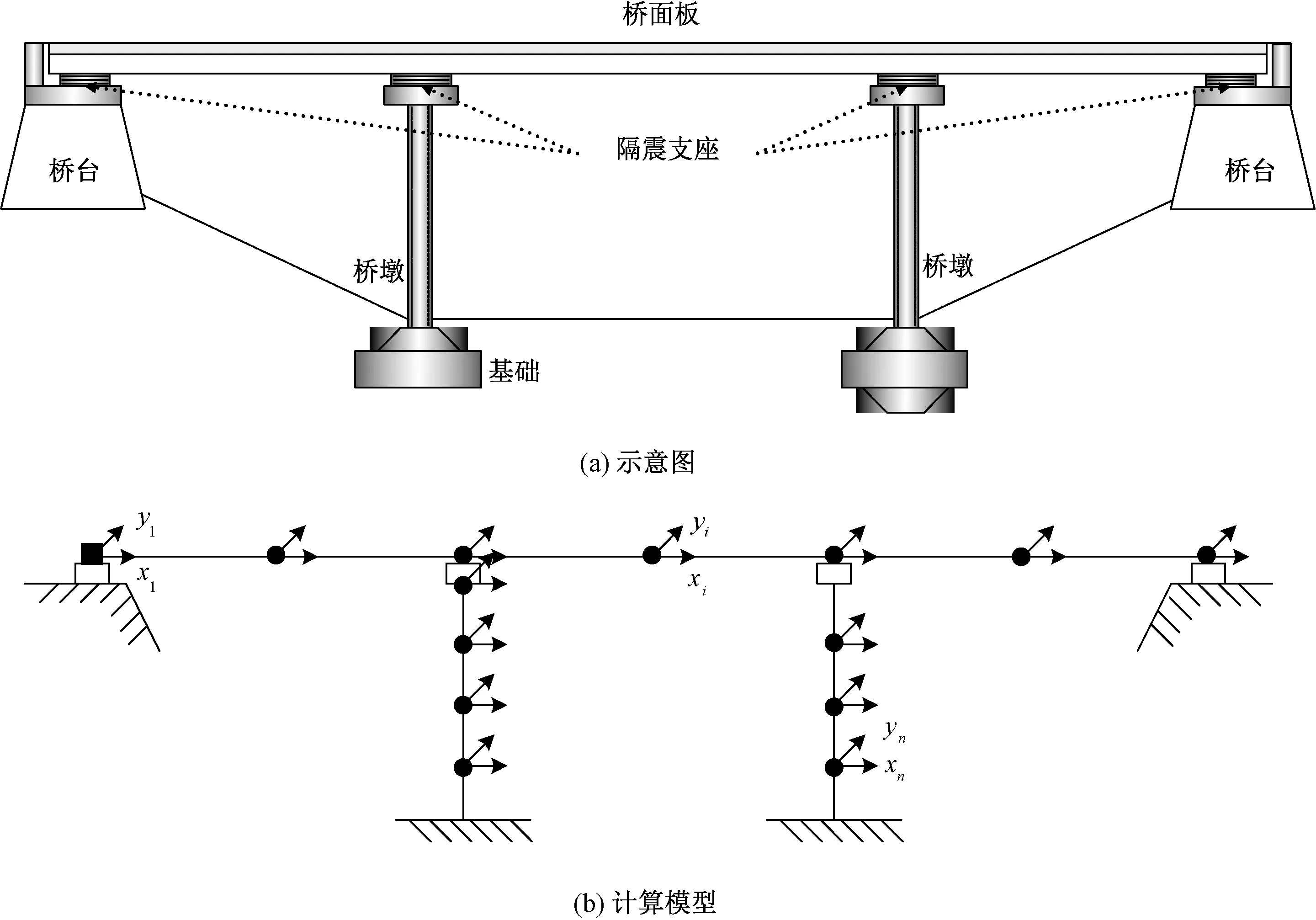
图5 隔震桥梁示意图和多自由度双向桥梁模型Fig.5 The schematic map of the isolated bridge and multi-degree freedom bidirectional bridge model

由于隔震支座的力-位移性质是非线性的，假设在很小的时间间隔Δt内加速度线性变化，运动方程的增量形式可以表述为：

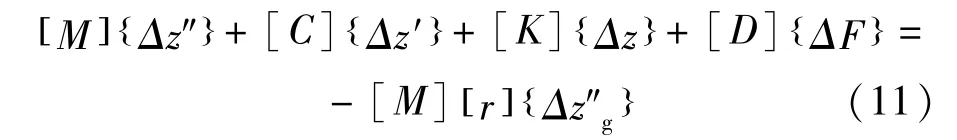
式中，{ΔF}是隔震支座恢复力增量，可表述为

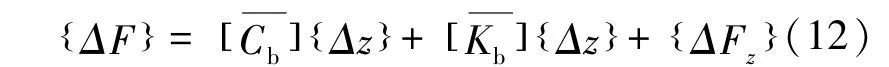
采用Newmark法求解运动方程的增量形式，方程（11）可改写为

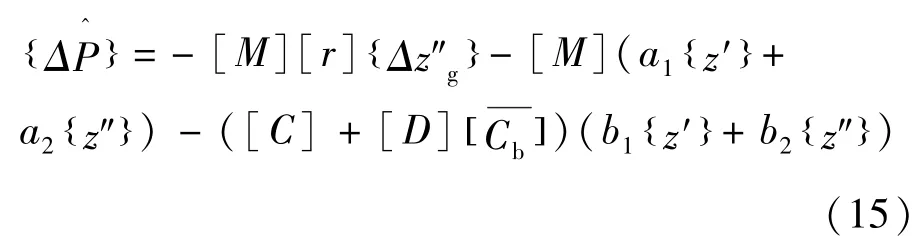
式中： a0＝ 6／Δt2，a1＝ -6／Δt，a2＝ -3，b0＝3／Δt，b1＝ -3，b2＝ -2／Δt。

由于隔震支座的非线性特性，在积分求解时要求时间步非常小。隔震支座滞变恢复力微分方程可以采用Runge-Kutta迭代法由t时刻的响应求解t+Δt时刻的响应，从而实现隔震桥梁动力响应时程分析。

3 数值算例

前文的推导以三跨桥梁为例，而方程对于桥梁的跨数是没有限制的，故本节以四跨连续梁桥为例进行分析，验证公式的多跨计算可靠性。

计算模型桥梁长120m，如图6所示。上部结构为预应力混凝土薄壁箱梁，混凝土强度等级为C40，预应力钢绞线为1860级，薄壁箱梁截面积为3.46m2；下部结构采用钢筋混凝土圆形桥墩，三个桥墩均高10m，圆形桥墩的截面惯性矩为0.548m4，混凝土强度等级为 C40，钢筋为HRB335级，不考虑桩土相互作用，桥墩与地面刚性连接。不考虑桥台回填土的影响，盖梁上不设剪力键。隔震桥梁采用铅芯橡胶支座和摩擦摆支座，非隔震桥梁采用普通盆式钢支座。计算过程中控制输入强度，保证支座不破坏。研究中心（Pacific Earthquake Engineering Research Center，PEER）。

图6 四跨桥梁结构Fig.6 Four-span bridge structure

表1 三条地震波及其峰值加速度Tab.1 Three kinds of seismic waves and their peak acceleration

常用隔震桥梁结构的规范化屈服力F0变化范围为0.02～0.20，本文对隔震支座设计时取F0＝0.08。 对 FPS支座，摩擦系数μ＝0.05；隔震支座隔震周期Tb变化范围为2～3s，本文取Tb＝2s。水平双向耦合地震作用下的支座的恢复力计算模型如前文所述。

表2为水平双向地震激励下，LRB隔震桥梁和非隔震桥梁中间桥墩基础剪力、桥面的绝对加速度、中间桥墩和桥台处支座相对位移反应的峰值。从数据对比中可以看出隔震结构的桥面加速度、桥墩剪力均有明显的降低，这说明隔震支座可以大大降低结构的地震响应，减小地震能量的输入。两处支座的位移值基本相差不多，说明上部结构在整个反应中变形很小，也符合前文的计算假定。

表2 LRB隔震和非隔震桥梁地震反应峰值Tab.2 Seismic response peak of LRB isolation and non-isolation bridges

图7显示Kobe地震波作用下LRB隔震和非隔震桥梁中间桥墩基础剪力时程变化曲线，与非隔震桥梁相比，LRB隔震桥梁中间桥墩的基础剪力减小很多，大约减少了70% ～90%。

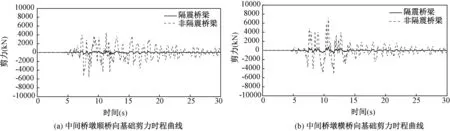
图7 Kobe地震波输入时LRB隔震和非隔震桥梁中间桥墩基础剪力时程曲线Fig.7 The time-history curve of shear force of middle pier foundation of LRB isolation and non-isolation bridges under Kobe seismic wave

图8显示了Kobe地震波作用下LRB隔震和非隔震桥梁横桥向桥面加速度时程变化曲线，可以看出在Kobe地震作用下LRB隔震桥梁横桥向桥面加速度大约减少了60%～80%。对于桥梁顺桥向，由表2数据可以看出在Loma Prieta地震作用下桥梁反应最大，LRB隔震桥梁顺桥向桥面加速度大约减少了70%～90%。

图8 Kobe地震波输入时LRB隔震和非隔震桥梁横桥向桥面加速度时程曲线Fig.8 The acceleration time-history curve of LRB isolation and non-isolation bridges floor in transverse direction under Kobe seismic wave

图9和图10分别显示了在Kobe水平双向地震作用下，中间桥墩和桥台处支座位移在桥梁纵向和横向时程变化曲线，桥墩、桥台处纵向峰值支座位移分别为17.06cm和17.89cm，对应桥墩、桥台处横向支座位移分别为23.23 cm和24.81 cm，中间桥墩处支座位移略小于桥台处的支座位移，这是由于桥台比中间桥墩刚度大的原故。支座的大变形说明了由于金属铅的变形消耗了大量的地震能量，从而减小了结构重要部件可能的损伤。

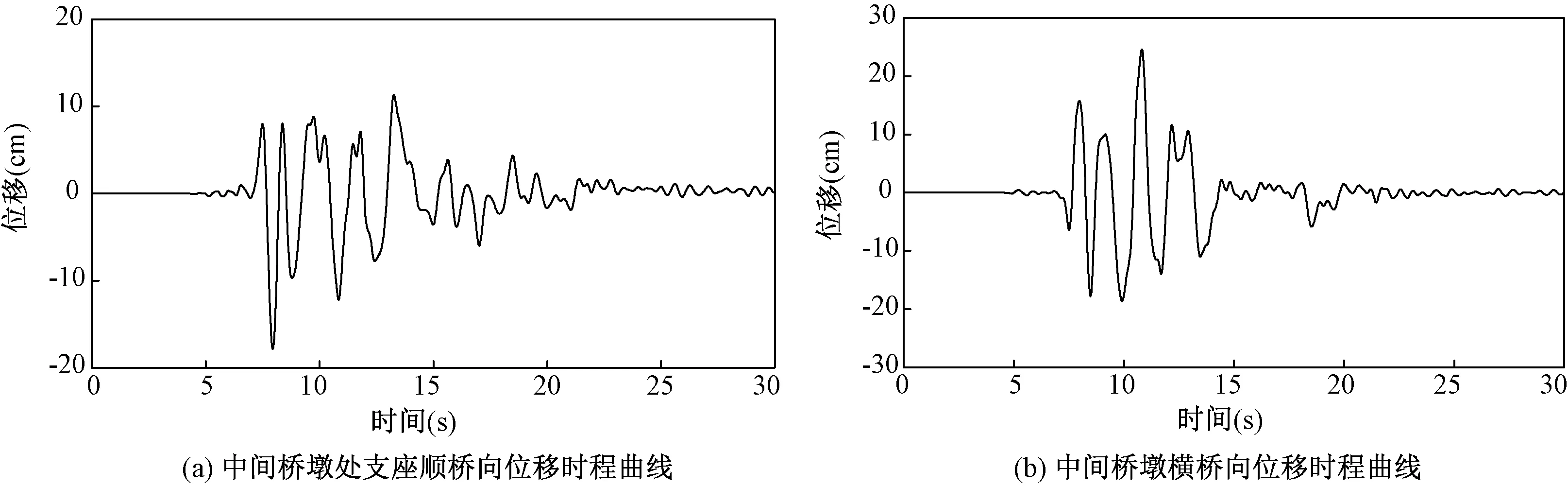
图9 Kobe地震波输入时LRB隔震桥梁中间桥墩处支座位移时程曲线Fig.9 The displacement time-history curve of bearing at middle pier of LRB isolation bridge under Kobe seismic wave

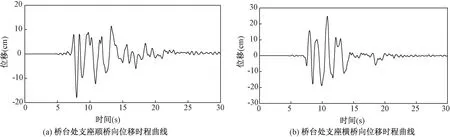
图10 Kobe地震波输入时LBR隔震桥梁桥台支座位移时程曲线Fig.10 The displacement time-history curve of bearing of LBR isolation bridge abutment under Kobe seismic wave

表3为水平双向地震激励下，FPS隔震桥梁和非隔震桥梁中间桥墩基础剪力，桥面中心处的绝对加速度、中间桥墩和桥台处FPS相对位移反应的峰值。

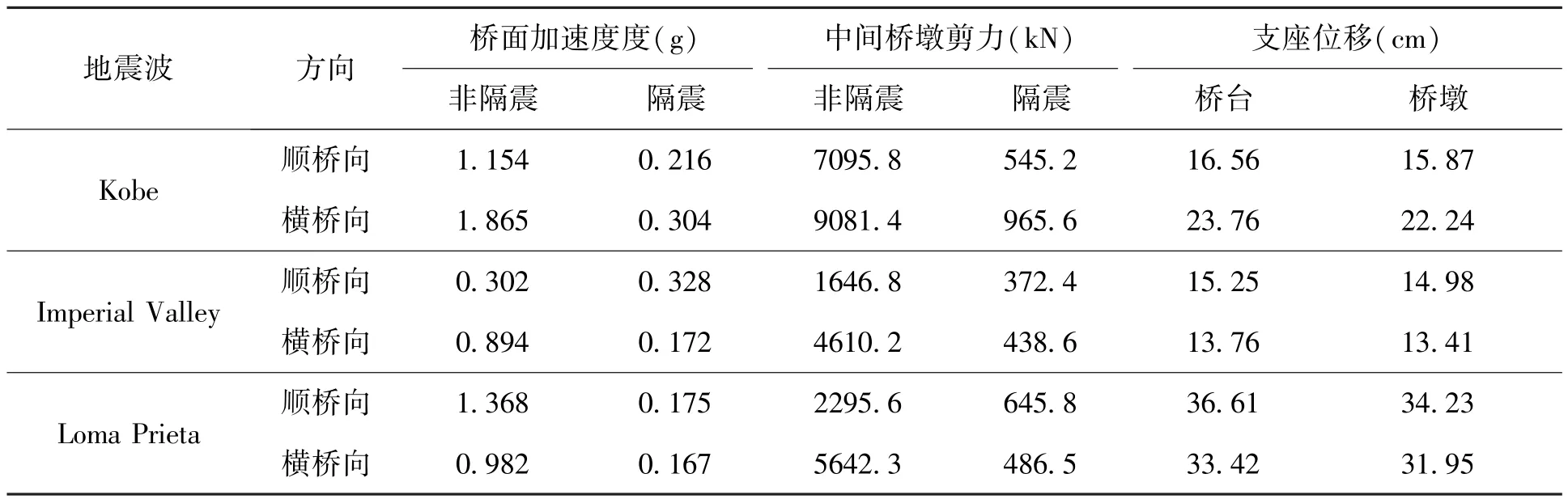
表3 FPS隔震和非隔震桥梁地震反应峰值Tab.3 Seismic response peak of FPS isolation and non-isolation bridges

表3得出的结论与表2一致，FPS隔震结构的桥面加速度、桥墩剪力均有明显的降低，这说明FPS隔震支座也可以大大降低结构的地震响应，减小地震能量的输入。两处支座的位移值基本相差不多，说明上部结构在整个反应中变形很小，符合弹性假定。支座的大量摩擦耗能减小了结构的响应。

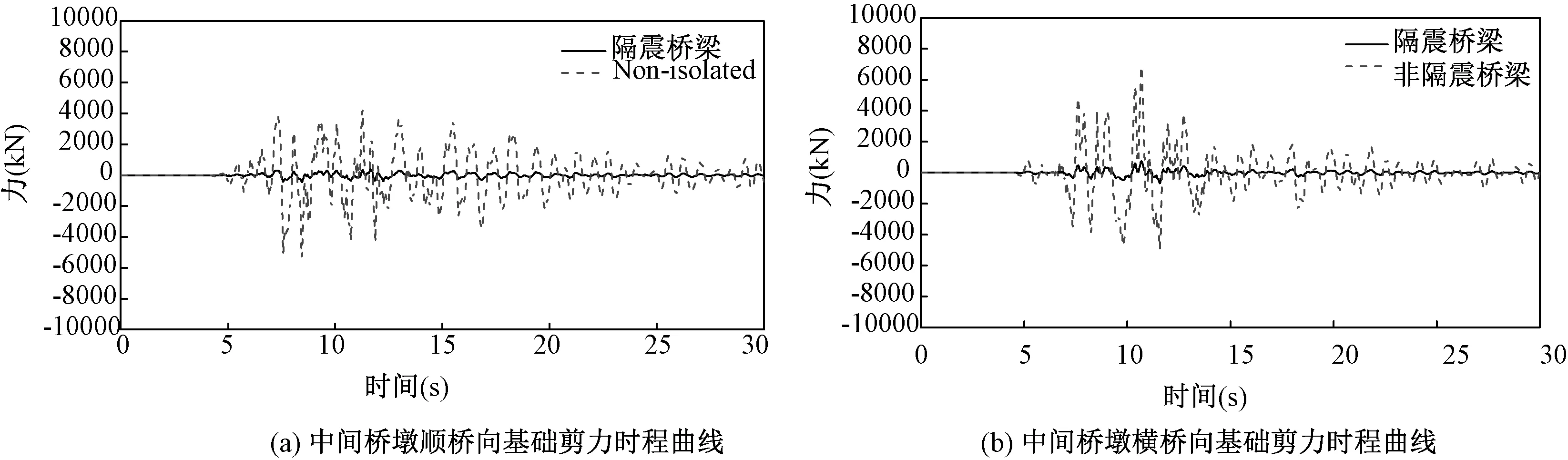
图11 Kobe地震波输入时FPS隔震和非隔震桥梁中间桥墩基础剪力时程Fig.11 The shear force time-history curve of middle pier foundation of FPS isolation and non-isolation bridges under Kobe seismic wave

图11显示Kobe地震波作用下FPS隔震和非隔震桥梁中间桥墩基础剪力时程变化曲线以及桥面加速度时程变化曲线，与非隔震桥梁相比，FPS隔震桥梁中间桥墩的基础剪力减小很多，大约减少了70%～80%。

图12显示Kobe地震波作用下FPS隔震和非隔震桥梁横桥向桥面加速度时程变化曲线。可以看出FPS隔震桥梁桥面加速度减小很多，大约减少了60% ～80%。表3显示在Loma Prieta地震作用下桥梁顺桥向桥面加速度反应最大，FPS隔震桥梁桥面加速度减小大约87%。

图12 Kobe地震波输入时FPS隔震和非隔震桥梁横桥向桥面加速度时程Fig.12 The acceleration time history curve of FPS isolation and non-isolation bridges floor in transverse direction under Kobe seismic wave

4 结论

本文对铅芯橡胶支座与摩擦摆隔震支座进行了理论分析，提出了对应的简化计算模型。在考虑支座双向耦合恢复力模型的基础上，给出了多跨连续隔震桥梁的数值计算方法，以某四跨连续桥梁为算例进行了时程分析，可以得到以下结论：

（1）水平双向地震激励下，隔震桥梁与非隔震桥梁相比，桥面的绝对加速度、桥墩的剪力均有明显的降低；支座的滞回位移大量消耗了地震的输入能量，有效降低了结构的地震响应。

（2）在个别地震波计算时，减震效果不明显，这主要与结构特性和地震波特性有关，隔震支座不能保证对所有的结构和地震动都适用。

（3）两种支座的耗能机理不一样，减震效果都很好，对于特定的桥梁选取哪一种支座进行减震仍需要进一步的研究。

［1］ Skinner R I，Robinson W H，Mcverry G H.工程隔震概论［M］.谢礼立，周雍年，赵兴权，译.北京：地震出版社：1996.

［2］ Mokha A S， Constantinou M C， Reinhorn A M.Experimentalstudy and analyticalprediction of earthquake response of a sliding isolation system with spherical surface ［R］.Technical report NCEER-90-0020.State University of New York at Buffalo；1990.

［3］ Mokha A S， Constantinou M C， Reinhorn A M.Teflon bearings in base isolation I： testing ［ J］.Journal of Structural Engineering， 1990，116：438-454.

［4］ Constantinou M C， Papageorgiou A S.Stochastic response of practical sliding isolation systems ［J］.Probabilistic Engineering Mechanics， 1990，5（1）：27-34.

［5］ Constantinou M C， Caccese J， Harris H G.Frictional characteristicsofTeflon-steelinterface under dynamic conditions ［J］. Earthquake Engineering and Structural Dynamics， 1987， 15：751-759.

［ 6 ］ Zayas V，Low S S，Mahin S A.A simple pendulum technique forachieving seismic isolation ［J］.Earthquake Spectra， 1990， 6（2）：317-333.

［7］ Tsopelas P， Constantion M C， Kim Y S， et al.Experimental study of FPS system in bridge seismic isolation ［J］.Earthquake Engineering＆ Structural Dynamics， 1996， 25（1）：65-78.

［8］ 刘文光.橡胶隔震支座力学性能及隔震结构地震反应分析研究［D］.北京：北京工业大学，2003.

［9］ 王志强.隔震桥梁分析方法及设计理论研究［D］.上海：同济大学，2000.

［10］ Kumar M， Whittaker A S， Constantinou M C.An advanced numerical model of elastomeric seismic isolation bearings ［J］.Earthquake Engineering ＆Structural Dynamics， 2015， 43（13）：1955-1974.

［11］ Ryan K L， Kelly J M， Chopra A K.Nonlinear model for lead-rubber bearings including axial-load effects［J］.Journal of engineering mechanics， 2005， 131（12）： 1270-1278.

［12］ Huang W H， Fenves G L， Whittaker A S， Mahin S A.Characterization of seismic isolation bearings for bridges from bi-directional testing［R］.Proceedings ofthe 12th World Conference on Earthquake Engineering，New Zealand Society for Earthquake Engineering， Auckland， New Zealand， Paper No.2047-2048.

［13］ Mokha A S， Amin N， Constantinou M C， et al.Seismic isolation retrofit of large historic building［J］.Structural Engineering， 1996， 122（3）：298-308.

［14］ Structural design and earthquake observation of a seismic isolated building using friction pendulum system.Proc.of the 7th WCSI［C］.Assisi， Italy，October 2-5，2001.

［15］ 李大望，周锡元，王东炜.摩擦摆系统振动性态的进一步分析［J］.振动工程学报，2001，14（3）：330-333.

［16］ Ferraioli M， Malangone P.Nonlinear modeling for dynamic analysis of base-isolated structures［C］.In：Proceedings of 11th European conference on Earthquake Engineering， 1998， Paper No.53.

［18］ Palazzo B， Pett L.Stochastic response comparison between base isolated and fixed-base structure ［J］.Earthquake Spectra， 1997， 13（l）：77-96

［19］ Park Y J， Wen Y K， Ang A H S.Random vibration of hysteretic systems under bi-directional motions［J］.Earthquake Eng Struct Dyn， 1986， 14（4）：543-557.