桥梁铅芯橡胶支座参数的优化设计研究

沈国锋林均岐刘金龙林庆利

（1.中国地震局工程力学研究所，中国地震局地震工程与工程振动重点实验室，黑龙江哈尔滨 150080；2.中通钢构建设股份有限公司，山东 聊城 252000）

0 引言

减、隔震技术是20世纪60年代出现的一项结构抗震技术，目前在桥梁结构的抗震设计中已得到广泛应用，如今有一些采用减、隔震技术设计的桥梁已经受过地震的考验。例如，新西兰Te Teko桥、美国Eel River桥以及日本阪神地震中6座采用了铅芯橡胶支座的桥梁，这些桥梁在地震中表现了良好的抗震性能，有力地证明了减隔震技术在工程中的有效性［1］。

铅芯橡胶支座由于制作简单、安装便利，被认为是一种较为理想的减、隔震装置，大量实验表明：铅芯橡胶支座的力学模型可以由屈服力、屈服前刚度、屈服后刚度三个参数控制。朱东生等［2］对铅芯橡胶支座的这三个动力参数在单独变化时桥梁结构的地震响应规律进行了研究。之后，李建中等［3-4］以地震力、梁体位移为优化标准，王凯［5］以支座最大耗能为优化标准，杨风利、张常勇等［6-7］针对铁路桥梁以上部结构纵向位移和考虑行车安全性评价指标为优化条件，三人分别对铅芯橡胶支座的三个动力参数进行了优化，但其动力参数与桥梁结构本身有着怎样的关系并没有给出。

合理选择铅芯橡胶支座的参数，能够最大限度地发挥减、隔震作用，如果选择不当，反而会因为地震动的不确定性导致桥梁结构产生更严重的破坏；由此可见，正确选用铅芯橡胶支座的动力参数是减小地震反应的关键所在，它可以使结构的内力和位移在地震动作用下都处于可控范围内。然而，研究发现当前有关这一课题的研究还相对较少，并且现有成果多侧重于探讨桥梁结构在不同铅芯橡胶支座动力参数下地震响应的变化规律，而对于采用不同设计参数的桥梁结构如何合理选择铅芯橡胶支座的动力参数涉及很少。针对这一问题，本文建立了多个桥梁工况进一步研究了铅芯橡胶支座的动力参数与结构设计参数（桥墩刚度、上部结构质量）之间的内在关系，旨在为今后桥梁工程更加合理地选择铅芯橡胶支座的动力参数提供依据。

1 铅芯橡胶支座的力学模型

铅芯橡胶支座在进入屈服阶段后会表现出强烈的非线性，大量支座试验表明［8-9］，支座的荷载-位移曲线呈现出如图1［10］所示的滞回环。其中，滞回环所包围面积的大小即是支座所耗散的能量，滞回环的形状影响结构的力学特性，因此，滞回环的描述对结构的地震响应十分重要。为了描述滞回环，国内外学者提出了多种滞回模型，主要有双折线模型和光滑滞回模型，而应用最广泛的是光滑可变微分方程—Bouc-Wen模型，Bouc-Wen微分模型已被大量应用于结构非线性分析中。

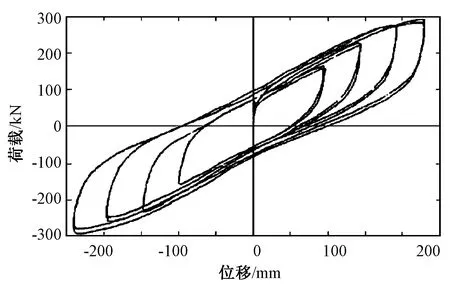
图1 铅芯橡胶支座试验的滞回曲线Fig.1 Hysteresis curve of lead rubber bearing test

Bouc-Wen 模型，首先是由 Bouc［11］于 1967 年提出的一种光滑滞回模型，之后不断有学者对其进行改进，其中Park等［12］的改进是现在工程中应用最广泛的。滞回系统的力与变形的关系采用Park， Wen and Ang（1986）建议的公式，见式（1）。

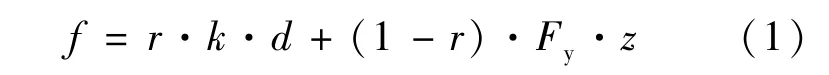
式中：k为初始刚度；Fy为屈服力；r为第二刚度系数（屈服后刚度与屈服前刚度的比值）；d为两节点的相对变形；z为滞回响应内部参数，使用 Wen［13］（1976）建议的微分方程计算，见式（2）。

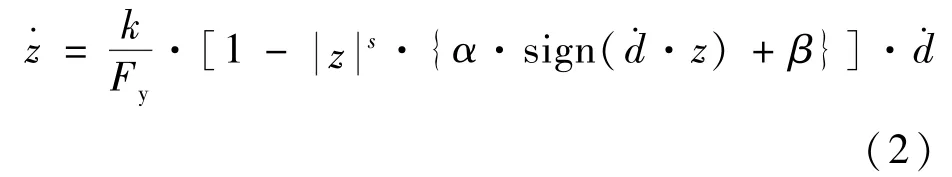
式中：α、β为决定滞回曲线形状的参数，需满足｜α｜+ ｜β｜＝1.0；α、β 直接影响系统的非线性刚度和非线性阻尼特性，α+β＞0时为软化系统，α+β＜0时为硬化系统，滞回系统中的耗能能力由滞回环的面积决定，面积越大耗能能力越强。在软化系统中（β-α）值越小耗能能力越强。其中α不可为负，否则系统将不稳定。s为决定屈服点的转移区域大小的常数；d为两节点间变形的变化率。均是变量对时间的导数。

根据《公路桥梁铅芯橡胶支座》（JTT 822—2011）［14］，发现第二刚度系数维持在0.15左右，故本文认定第二刚度系数r＝0.15。现在，Bouc-Wen模型还有支座的两个动力参数尚未确定，即屈服前刚度（初始刚度）和屈服力。

根据铅芯橡胶支座模型的试验研究［15］，建议取 s＝2，α ＝0.5，β＝0.5；取 r＝0.15、k＝1.0、Fy＝1.0、s＝2.0、α ＝0.5、β＝0.5，对应支座的滞回曲线见图2。

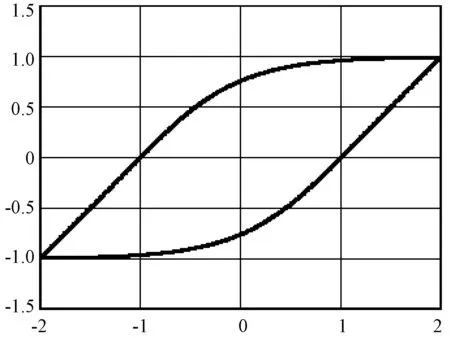
图2 Bouc-Wen模型铅芯橡胶支座的滞回曲线Fig.2 Hysteresis curve of Bouc-Wen model lead rubber bearing

对支座屈服前刚度进行无量纲化处理，取支座屈服前刚度与桥墩刚度的比值，称为屈服刚度比，该比值控制在0.11～0.25内变化，共有6个刚度比值。对于屈服力，同样作无量纲化处理，取屈服力的总和与桥梁上部结构重量的比值，称为屈服重力比，假定在0.01～0.20范围内变化，增值幅度为0.01，共有20个屈服重力比值。

2 桥梁有限元分析模型

选用一联三跨连续梁桥进行分析，采用单墩式桥墩，桥梁跨径为每跨20m，桥墩高度为10m。

针对不同的桥梁，根据实际工程中桥梁的基本情况［2-4］，将桥梁上部结构均布质量分别设定为 80kN／m、100 kN／m、120 kN／m。 根据规范［16-17］采用减、隔震设计的桥梁，其耗能部位位于铅芯橡胶支座，即使在E2地震作用下，上部结构、桥墩、基础也不会产生损伤，基本保持在弹性工作范围内。另根据文献［10］，通常采用隔震设计后，在设计地震动作用下，桥墩因受到隔震装置的保护不发生塑性变形，可以采用线性梁单元来描述，但应仔细考虑其质量分布。因此，在本文中桥墩单元、上部结构单元均采用梁单元模拟，整个结构只有支座单元进入非线性阶段。

为了得到不同桥墩刚度下支座的优化参数，参照文献［2，3，4］，建议桥墩尺寸分别设置为1.2m ×1.2m、1.4m ×1.4m、1.6m ×1.6m，在这里桥墩的尺寸仅仅是一种刚度的代表值，见表1。桥墩采用C40混凝土，弹性模量3.25×104MPa。

表1 桥墩的计算参数Tab.1 Calculation parameters of pier

对不同桥墩刚度、上部结构质量进行随机组合，共有9种工况，见表2。

and superstructure quality

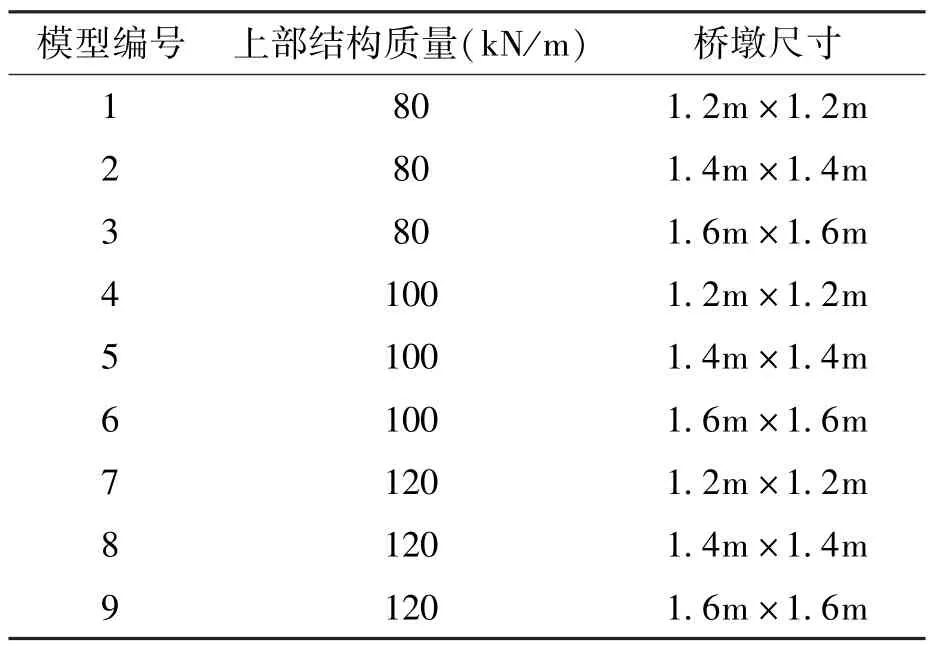
表2 桥墩刚度与上部结构质量的随机组合Tab.2 Random combination of pier stiffness

3 地震动的选择

对于结构抗震分析，尤其是当结构进入非线性阶段，采用不同的地震动输入会使结构的地震反应产生很大的差别。规范中的设计谱是结构抗震设计的依据，是地震作用大小的标准，因此用时程法进行抗震分析时输入地震动的反应谱也应与规范中的设计反应谱一致。采用按规范设计谱合成的人工地震动进行时程分析所得结果之间具有更好的可比性［18］。

我国《公路桥梁抗震设计细则》［17］和《城市桥梁抗震设计规范》［16］均规定不得少于3组（对于地震反应分析结果，3组需取最大值，7组可以取平均值），本文根据规范规定的反应谱拟合生成了Ⅱ类场地下的3条人工地震动，它们具有相同的反应谱。地震动加速度时程曲线见图3，地震动反应谱曲线见图4。

为使采用不同设防烈度的桥梁更便捷地选出支座参数，本文选择了5种不同的设计谱峰值，具体的做法是对上述Ⅱ类场地下的人工地震动进行峰值调整，设计谱峰值分别调 整 为 0.675g、 0.765g、 0.8775g、1.024g、1.17g。

综上所述，本文选取了Ⅱ类场地下的3条人工地震动、5个设计谱峰值、6种支座刚度与桥墩刚度比值、20种屈服重力比、3种上部结构质量、3种桥墩刚度，具体参数见表3。

图3 地震动加速度时程曲线Fig.3 Acceleration time history curve of ground motion

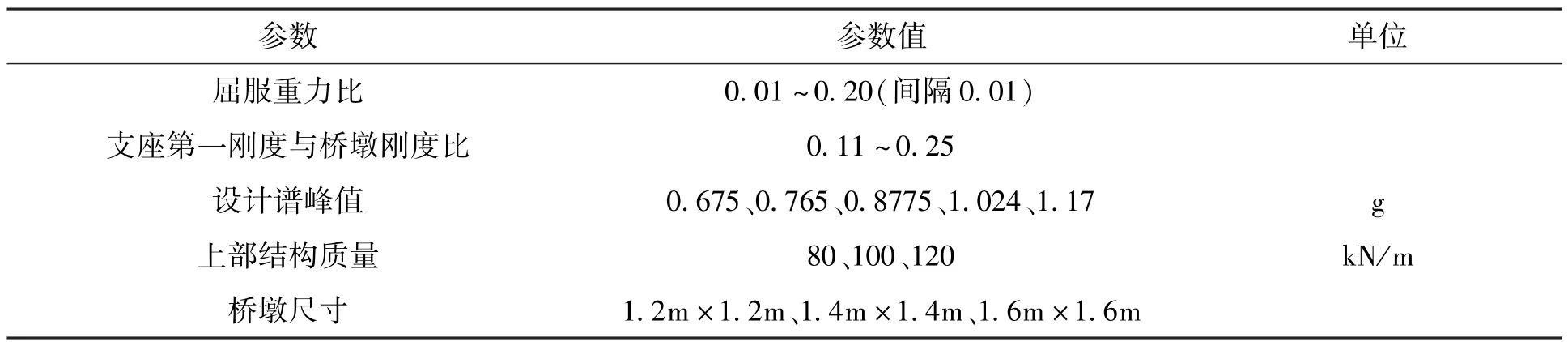
表3 桥梁模型、支座参数、地震水平工况表Tab.3 Bridge model， support parameter， earthquake level working condition

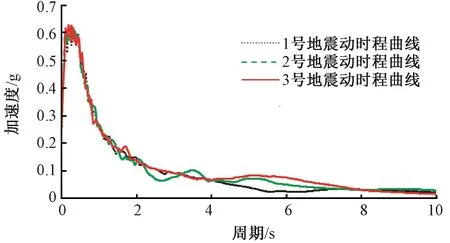
图4 地震动加速度反应谱曲线Fig.4 Acceleration response spectrum curve of ground motion

4 铅芯橡胶支座优化参数的确定

减、隔震结构设计利用引进的柔性装置，一方面由于柔性装置的存在延长了结构的基本周期，避开地震动能量集中的范围，减小了结构地震力；另一方面结构基本周期的延长，会导致结构位移的增大。减、隔震设计的目标应该是控制上部结构的位移不应太大，同时结构地震力应尽可能地减小。对于桥梁结构，减、隔震设计主要控制的参数有墩梁相对位移、桥墩底部剪力和桥墩底部弯矩。故本文设定的优化设计原则为控制上部结构位移不能太大，同时最大程度地减小墩底剪力和墩底弯矩。

对于采用减、隔震设计的桥梁，主要是对计算模型进行E2地震作用下的地震反应分析［14-15］。

输入前文生成的3条人工地震动，把设计谱幅值调整为0.675g。横桥向由于桥墩刚度比较大，一般不采用减、隔震设计，故本文输入地震动仅对纵桥向而言。

4.1 屈服重力比的确定

以Ⅱ类场地下上部结构均布质量为100 kN／m、桥墩尺寸为1.4m×1.4m的工况为例，当设计谱峰值为0.675g时，通过地震反应分析给出了刚度比一定时，纵桥向墩梁相对位移、墩底剪力和墩底弯矩随屈服重力比的变化曲线，见图5～图7。

从图5～图7可以看出，墩梁相对位移随着屈服重力比的增大迅速减小，当屈服重力比取到0.05时趋于稳定，而墩底剪力和墩底弯矩随屈服重力比先减小后增大，在0.01～0.20屈服重力比之间存在极小值。这样可以把地震反应分为三部分来处理，分别为A、B、C三个区域，通过对A、B、C三个区域比较可以得到：（1）A与B比较可知，B部分的墩梁相对位移较小，而墩底剪力和墩底弯矩大小比较接近；（2）B与C比较可知，两部分的墩梁相对位移相当，但C区域的墩底剪力和墩底弯矩有较大增加。由此可见，只有B区域最符合本文制定的减、隔震优化设计原则，即当屈服重力比取值在0.05～0.08时，认为此时的支座参数可以使减、隔震设计达到最优。

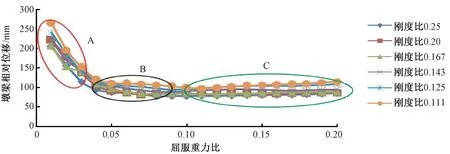
图5 墩梁相对位移与屈服重力比变化关系Fig.5 Relationship between the relative displacement of pier-beam and yield gravity ratio

采用同样的方法，可以得到其他设计谱峰值和工况下的最优屈服重力比，见表4。

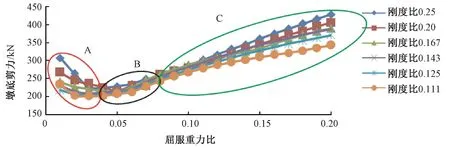
图6 墩底剪力与屈服重力比变化关系Fig.6 Relationship between bottom shear of pier and yield gravity ratio

图7 墩底弯矩与屈服重力比变化关Fig.7 Relationship between bottom bending moment of pier and yield gravity ratio

表4 Ⅱ类场地下各工况的最优屈服重力比Tab.4 The optimal yield gravity ratio of different working conditions in field II

4.2 支座屈服前刚度的确定

理论上支座的屈服前刚度越小，地震响应的墩底剪力和墩底弯矩越小，而墩梁相对位移越大，但是根据《公路桥梁抗震设计细则》［17］，橡胶型减隔震装置在E2地震作用下的剪切变形要小于250%，因此有必要确定不同工况下支座屈服前刚度的大小。其中，剪切位移＝剪切变形×支座有效橡胶总厚度。根据相关规范可取E2地震作用下位移限值为150mm。

现在问题转化为，如何利用墩梁相对位移限值确定支座屈服前的刚度。

同样以Ⅱ类场地下的设计谱峰值取0.675g时的工况为例，进行屈服前刚度的确定。由上一小节已经确定了支座的屈服力范围，假定屈服力范围内的每一个位移值具有相同的权重系数，对屈服力范围内的位移取平均值，认为此平均值为此屈服前刚度的位移值，则可以计算各屈服刚度比下的墩梁相对位移。

以上部结构均布质量为100kN／m、桥墩尺寸为1.2m×1.2m的工况为例，给出了不同屈服刚度比下的加权位移值，见表5。

采用幂函数对刚度比、位移值进行拟合分析（原因是从理论上分析，当刚度比趋于0时，墩梁相对位移会趋于无穷），见图8。

从图8可以看到墩梁相对位移随刚度的变化趋势，采用幂函数拟合可得：

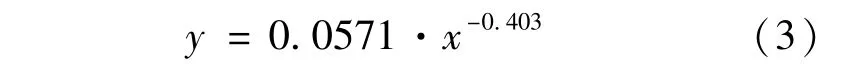
式中，y代表墩梁相对位移，单位m；x代表支座刚度与桥墩刚度的比值。

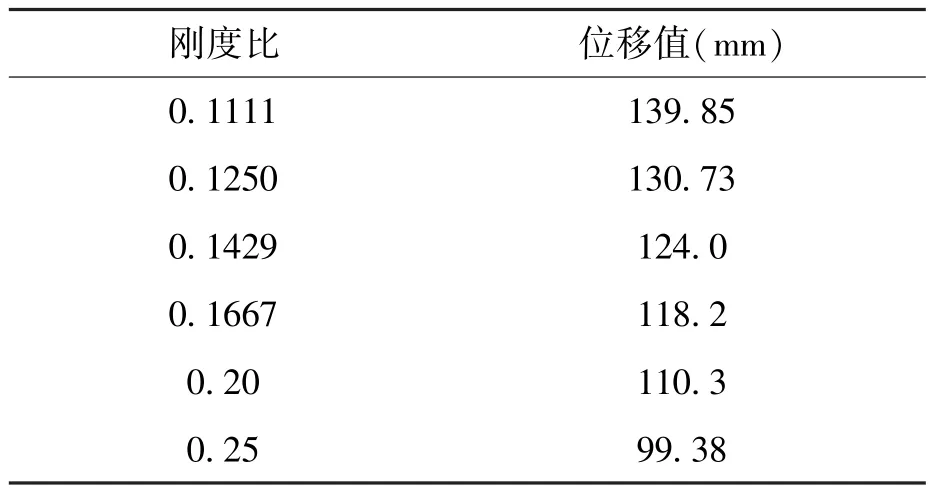
表5 不同刚度比下的加权位移值Fig.5 Weighted displacement values under different stiffness ratios

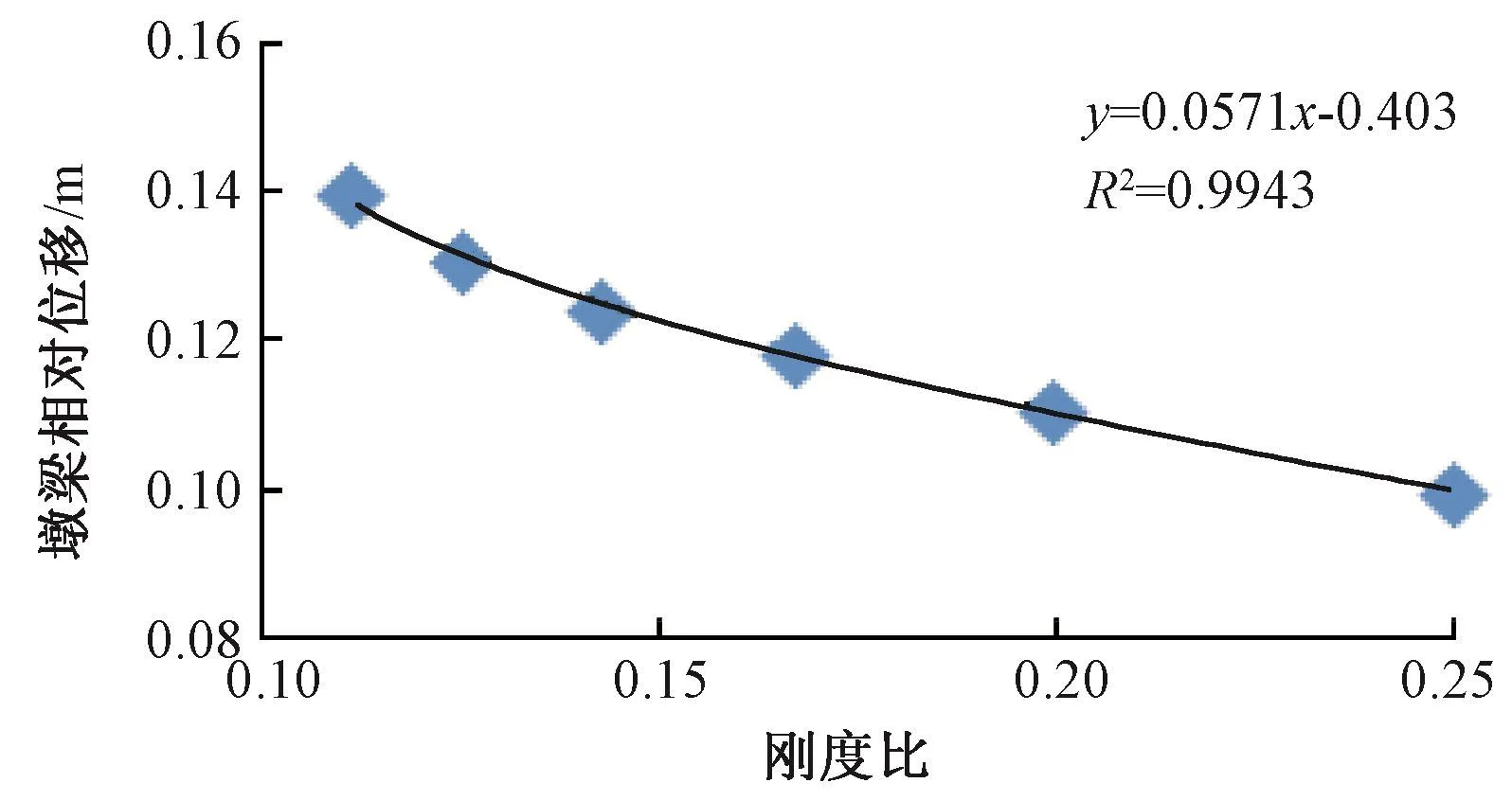
图8 刚度比与位移的拟合公式Fig.8 Fitting formula of stiffness ratio and displacement

本文设定的墩梁相对位移限值为150mm，把 y＝0.15代入式（3），得到 x＝0.091，即认为屈服刚度比取值为0.091时桥梁减、隔震效果可以达到最优。同理，可得到各个工况下支座刚度比的最优值，见表6。

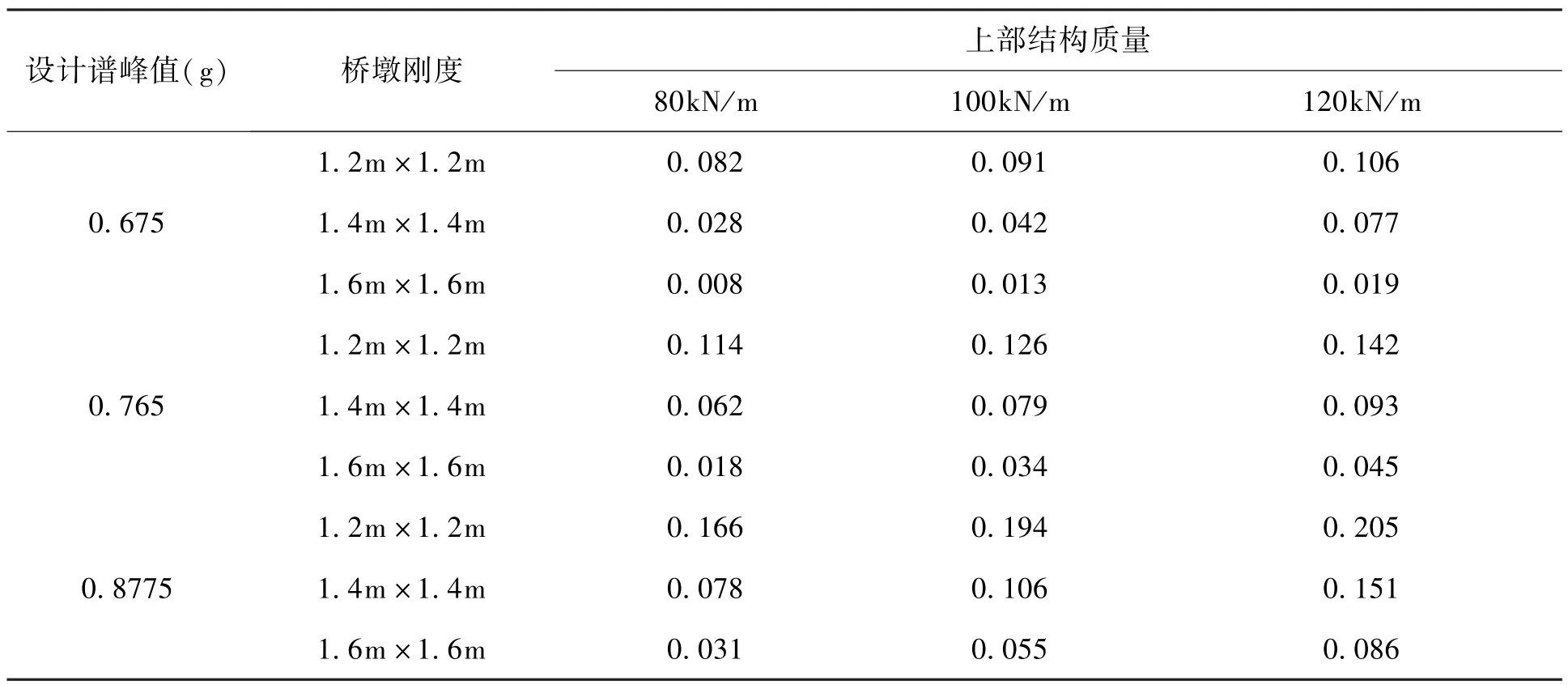
表6 Ⅱ类场地下各工况的最优刚度比Tab.6 Optimal stiffness ratio of different working conditions in field II

续表6

5 结论

本文建立了一座典型三跨连续梁桥的有限元分析模型，以Ⅱ类场地下合成的3条人工地震动为输入进行非线性动力时程分析，开展了不同桥梁工况下铅芯橡胶支座动力参数与桥墩刚度和桥梁上部结构质量的相关性研究，主要得出以下结论：

（1）通过非线性地震反应分析给出了各个工况下的墩底剪力、墩底弯矩、墩梁相对位移随屈服重力比的变化关系曲线，分析得到了屈服重力比的最优值。

（2）拟定优化标准为墩梁相对位移限值150mm、地震力越小越好，给出了墩梁相对位移与屈服刚度比的变化关系曲线，采用幂函数拟合得到了它们之间的计算公式，并由位移限值计算得到了屈服刚度比的最优值。

以上两点结论可为今后采用减、隔震技术的桥梁更加合理地选择铅芯橡胶支座提供参考。此外，应当指出本文仅考虑了纵桥向输入地震动，没有考虑横桥向和竖向地震动，对于多维地震动下铅芯橡胶支座动力参数的优化问题尚需在今后工作中进一步研究。

［1］ 叶爱君，管仲国.桥梁抗震［M］.北京：人民交通出版社，2011.

［2］ 朱东生，劳远昌，沈大元，等.隔震桥梁设计参数的研究［J］.土木工程学报，2000，33（5）：52-56.

［3］ 李建中，辛学忠.连续梁桥减震-隔震体系非线性地震反应分析［J］.地震工程与工程振动，1998，18（3）：67-73.

［4］ 李建中，袁万城，范立础.连续梁桥减、隔震体系的优化设计［J］.土木工程学报，1998，31（3）：47-54.

［5］ 杨风利，钟铁毅，夏禾.铁路简支梁桥减隔震支座设计参数的优化研究［J］.铁道学报，2006，28（3）：128-132.

［6］ 张常勇，钟铁毅，顾正伟，杨风利.铁路连续梁桥铅芯橡胶支座优化设计研究［J］.铁道学报，2012，34（5）：97-102.

［7］ 王凯.连续梁桥减隔震支座参数设计与优化［D］.成都：西南交通大学，2014.

［8］ 唐家祥，刘再华.建筑结构基础隔震［M］.武汉：华中理工大学出版社，1993.

［9］ 周福霖.工程结构减震控制［M］.北京：地震出版社，1997.

［10］ 范立础，王志强.桥梁减隔震设计［M］.北京：人民交通出版社，2001.

［11］ Bouc，R.Forced Vibration of Mechanical Systems With Hysteresis［C］.Proceedings ofthe 4th Conference on Nonlinear Oscillations. Prague，Czechoslovakia.1967.

［12］ Park， Wen， Ang.Random Vibration of Hysteretic Systems under bi-directional ground motions［J］.Earthquake Engineering and Structural Dynamics，1986，14（4）：543-557.

［13］ Wen， Y.K. Method ofRandom Vibration of Hysteretic Systems［J］.Journal of Engineering Mechanies Dvision， ASCE，1976，102（2）：249-263.

［14］ JT／T 822—2011 公路桥梁铅芯隔震橡胶支座［S］.北京：人民交通出版社，2012.

［15］ 葛俊颖.桥梁工程软件 midas Civil使用指南［M］.北京：人民交通出版社，2013.

［16］ CJJ 166—2011 城市桥梁抗震设计规范［S］.北京：中国建筑工业出版社，2012.

［17］ JTG／T B02-01—2008 公路桥梁抗震设计细则［S］.北京：人民交通出版社，2008.

［18］ 朱东生.桥梁抗震设计中几个问题的研究［D］.成都：西南交通大学，1999.