佛山地铁魁奇路地下换乘站抗震性能分析

龙喜安

（广州地铁设计研究院有限公司，510010，广州∥工程师）

1 工程背景

魁奇路站为佛山地铁2号线与广佛线换乘车站，其主体结构采用地下箱型框架结构（如图1所示）。车站有效站台中心里程处顶板覆土厚约3.2 m，底板埋深12.2 m。按GB 50909—2014《城市轨道交通结构抗震设计规范》第3.1.4条，地铁车站抗震设防烈度为7度，设计基本地震加速度值为0.10 g，设计地震分组为第一组，地震特征周期为0.35 s。根据《佛山市城市轨道交通二号线一期工程场地地震安全性评价报告》，50年超越概率10%所对应的地面平均峰值加速度为0.099 7 g，场地类别为Ⅲ类，E2地震作用下的抗震性能验算采用反应位移法计算，E3地震作用下结构的变形采用非线性时程分析法计算。车站范围地层的岩土物理力学参数如表1所示。

2 反应位移法抗震计算

反应位移法以一维土层地震反应分析计算得到的土层相对位移为基础，利用地下结构周围土层在地震时的变形值计算出力的大小，并以静荷载的形式作用在结构上，进而计算出地震作用下的结构内力［5］。地下结构周围土体作为支撑结构的地基弹簧，其弹簧刚度依据地基反力系数计算。车站结构采用梁单元进行模拟。

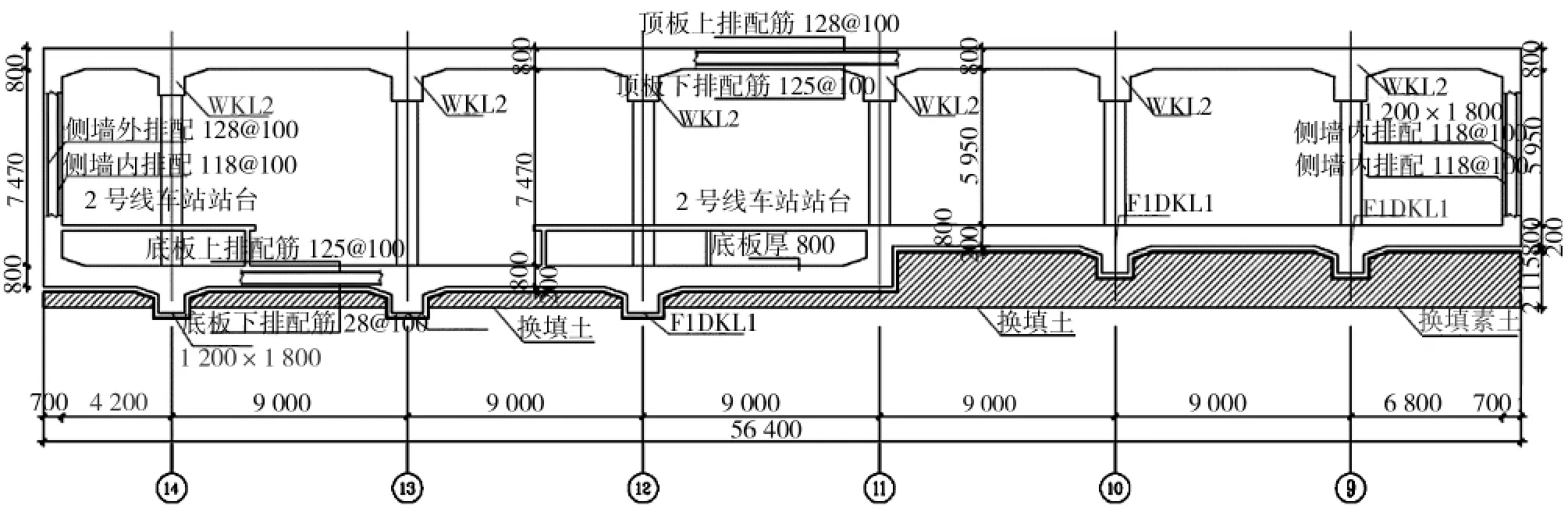
图1 车站主体结构横剖面图

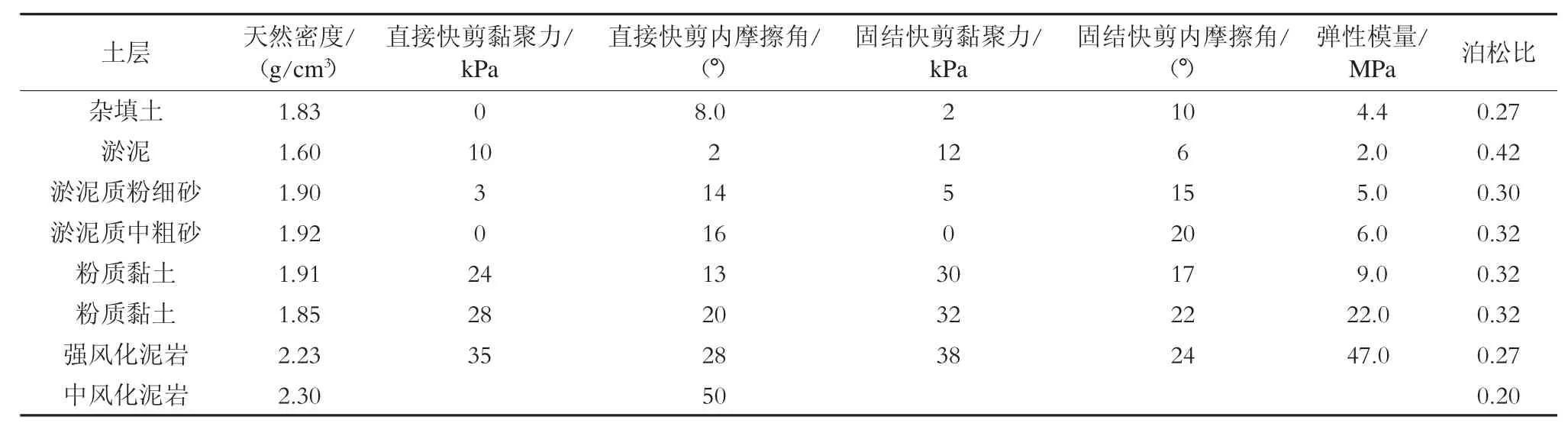
表1 地层物理力学参数

魁奇路站对应基本设计地震的地震动峰值位移Umax=0.07 m。按剪切波速＞500 m/s且其下卧土层的剪切波速均≥500 m/s的土层顶面为基准面，确定基准面埋深。强风化泥岩层剪切波速为430.00 m/s，中风化泥岩层剪切波速为822.14 m/s；按最不利情况进行取值，取基准面埋深H=17.65 m。

选取典型断面，建立车站二维结构计算模型，支座位移及等效地震荷载计算结果如表2所示，弹簧支座点布置见图2。

通过对车站结构进行静力计算和反应位移法抗震分析计算，选取车站主体结构标准段主要内力控制截面，逐一统计各工况下的内力设计值并进行配筋计算。标准段各工况下反应位移法与静力法计算结果对比如表3所示。

表2 弹簧支座点施加的支座位移和节点力

图2 标准段弹簧支座编号示意图

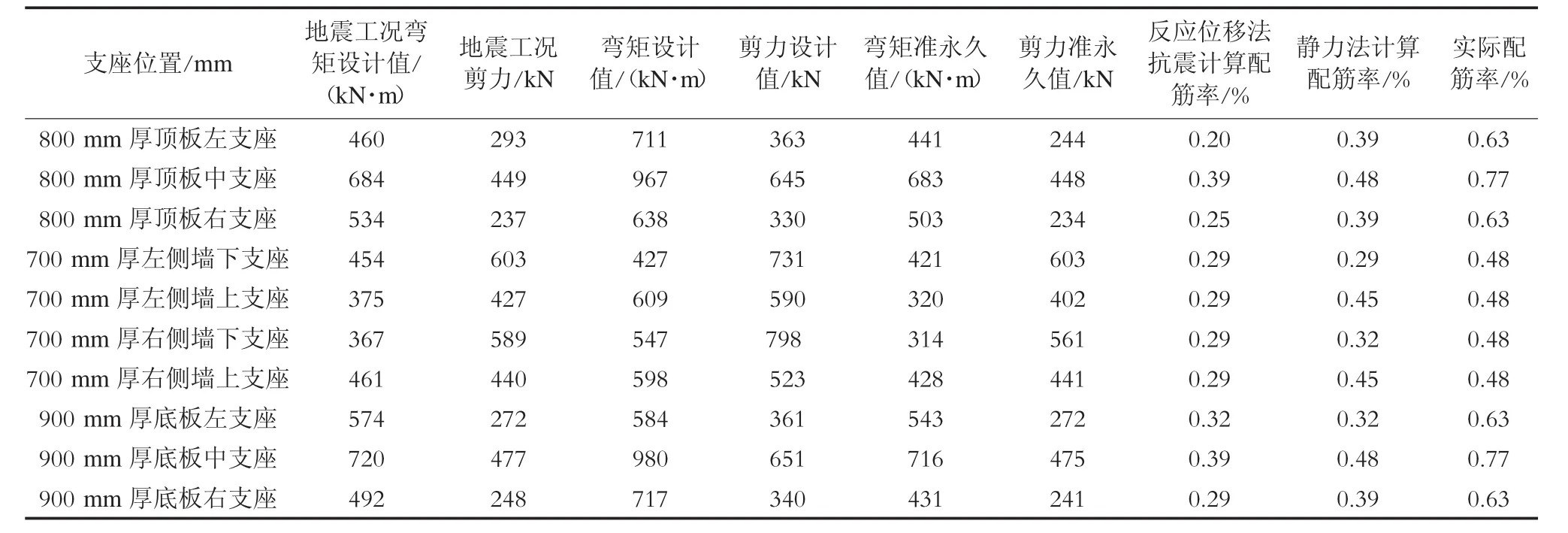
表3 各工况条件下反应位移法与静力法计算结果对比

由表3可知，结构实际配筋率由准永久荷载组合作用下的裂缝计算值控制，抗震工况不起控制作用。而且在地震工况下，车站的中柱轴压比为0.736，未超过其限值0.75，故中柱延性满足抗震要求。

3 非线性动力时程分析法

3.1 地震作用下动力有限元理论

动力有限元中先将结构进行离散化。在地震荷载作用下，具备n个自由度的整个结构离散系统在任一时刻t的动力平衡方程为：

Ma（t）+Cv（t）+Ku（t）=p（t） （1）

式中：

M——质量矩阵；

C——阻尼矩阵；

K——结构刚度矩阵；

a（t）——系统加速度向量；

v（t）——系统速度向量；

u（t）——位移向量；

p（t）——荷载向量。

地震作用输入采用振动法。假定设计地震作用基准面上各点的地震加速度在同一时刻均为ag（t）。令ar（t）为计算区域各点相对基准面的相对加速度，则运动方程变为：

Ma（t）+Cv（t）+Ku（t）=-Mag（t）（2）

地震惯性力作用在土体和结构上，模拟地震作用。地震加速度ag（t）通过地震加速度时程曲线进行输入。由于结构体系在动力反应作用下的受力为非线性状态，故动力平衡方程采用逐步积分法进行求解。

3.2 非线性地震动模拟模型

3.2.1 建立计算模型

根据结构的具体几何形状、荷载和受力特征，将实际的三维空间问题简化为二维平面应变问题，采用Midas GTS NX软件建立模型。结构及土层均按各向均质、各向同性黏弹性体考虑，建立分层半空间模型。结构采用梁单元，土层采用平面应变单元，土层单元尺寸约为1 m×1 m。时程分析法计算模型见图3。模型底面取至中风化泥岩层顶面，模型顶面取至地表面，模型侧面边界到结构的距离取结构水平宽度的3倍。动力荷载作用下，模型各层之间假定不发生脱离和相对滑动，且界面满足层间位移相互协调性。

计算模型同时考虑自重、地面超载和地震作用，在抗震分析工况前添加自重作用下的静力分析工况，在计算模型静力计算获得应力场后，再进行动力计算。

图3 时程分析法计算模型

3.2.2 土体内部阻尼

地震波荷载作用下，阻尼能使其能量衰减，是不可忽略。有限元软件求解有多种阻尼设置方法，主要包括Alphad和Beta阻尼、振型阻尼和单元阻尼等。不同振动模态情况下定义的阻尼比通常采用振型阻尼。振型阻尼中的Rayleigh阻尼矩阵具有计算方便、节约内存、计算精度较高等优点，因此被有限元软件广泛采用。

Rayleigh阻尼矩阵为：

C= αM+ βK （3）

其中：α和β为Rayleigh阻尼参数。α和β与粘性阻尼比ξ之间的关系为：

ξ= α /2ω + βω/2 （4）

式中：

ω——频率。

在第i振型及第j振型中，当ξ为固定值时，有：

α=2ωiωj（ξiωj-ξjωi）/（ωj2-ωi2）（5）

β=2（ξjωj-ξiωi）/（ωj2-ωi2）（6）

式中：

ωi——第i振型的结构频率；

ωj——第j振型的结构频率；

ξi——第i振型阻尼比，由试验确定；

ξj——第j振型阻尼化，由试验确定。

结构的自振特性主要由固有频率与振型两个因素构成，是重要的结构力学性能，决定了结构在地震荷载作用下的响应情况。因此，在进行地震荷载作用下的结构动力分析之前，先要进行模态分析。模态分析过程中应忽略阻尼的影响，并假定结构处于线弹性阶段。无阻尼作用的结构自由振动方程为：

Ma（t）+Ku（t）=0 （7）

经边界条件处理，得到结构广义特征值方程：

（K- ωz2M）φ =0 （8）

式中：

ωz——结构自振频率；

φ——振型向量。

进而得出特征行列式：

｜K- ωz2M｜ =0 （9）

通过特征值分析计算前两阶振型的自振频率。特征值分析时不施加任何阻尼（包括边界阻尼）及荷载，只有底面的边界固定。特征值分析结果见表4。

由表4可知，第1和第5振型的水平方向有效质量比例最高，分别达到35.6%和3.4%，故取这两阶振型的自振频率。第1及第5振型的自振周期分别为 2.331 3 s和 1.667 7 s。

表4 特征值分析结果表

3.3 非线性时程分析结果

根据工程场地地震安全性评价报告,按50年超越概率2%的水准,地震加速度点时间间隔为0.02 s，每组地震波加速度持续时间为40 s。进行时程分析时，将3条实际记录的加速度时程曲线调幅至设防地震烈度，作为输入地震波。输入3组人工合成地震波的加速度时程曲线。

为节约计算时间，每组地震波均截取0～25 s段的加速度时程曲线，时程分析持续时间设置为25 s，时间增量设置为0.1 s，中间值输出时间间隔设置为1 s。使用振型阻尼进行计算，输入第1阶和第5阶振型的周期和阻尼比，土体阻尼比取0.05。在进行计算前，需对测点进行预先设置。

3组地震波作用下结构断面主要发生剪切变形。第一组地震波作用下,负一层最大层间相对位移为17.01 mm，对应最大层间位移角为2.17×10-3，时间点为地震波作用后12.6 s；第二组地震波作用下,负一层最大层间相对位移为20.62 mm，对应最大层间位移角为2.63×10-3，时间点为地震波作用后18.7 s；第三组地震波作用下，负一层最大层间相对位移为29.4 mm（见图4），对应最大层间位移角为3.75×10-3（见图5），时间点为地震波作用后10.7 s。第三组地震波作用下发生的位移值最大，层间位移角小于规范限值4×10-3，满足抗震规范要求的弹性限值及弹塑性限值。

4 结论

（1）反应位移法分析结果中，地震工况作用下的内力设计值比静力作用下的内力设计值小；但结构按裂缝控制的配筋率比抗震计算和静力计算的配筋率均要大，结构实际配筋由准永久荷载组合作用下的裂缝计算控制，抗震工况不起控制作用。

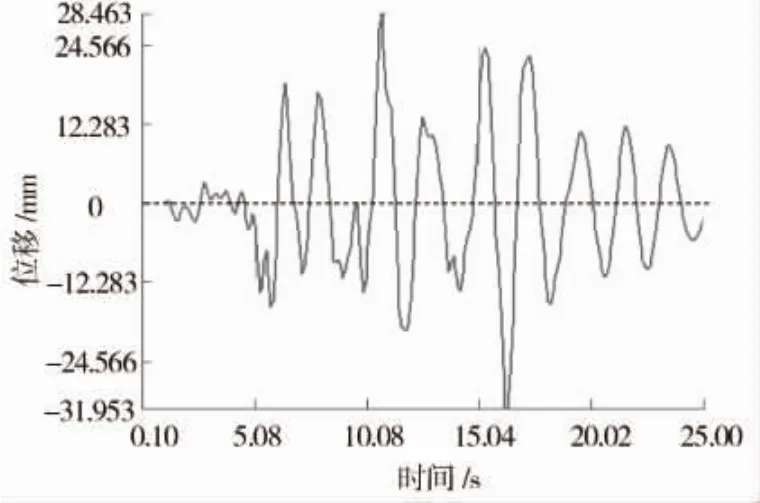
图4 负一层层间相对位移时程曲线（第三组地震波）

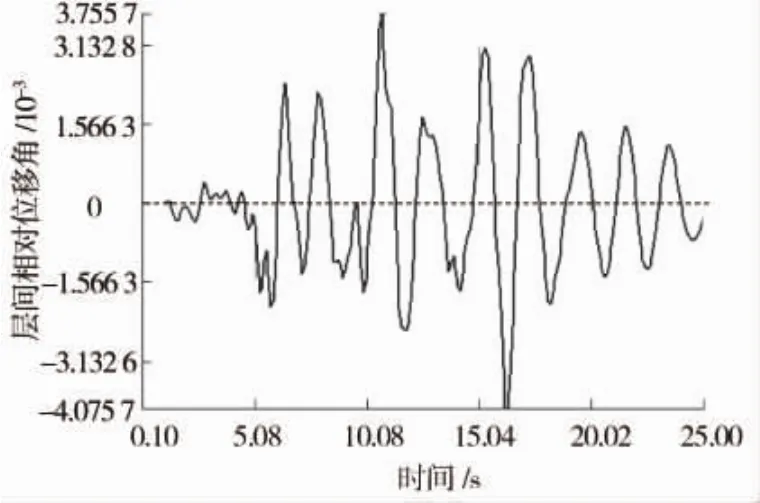
图5 层间相对位移角时程曲线（第三组地震波）

（2）非线性时程法对车站进行地震荷载下的动态模拟，反映了结构任意时刻的位移时程反应及变形规律；地震波作用下，结构主要发生横向剪切变形，随着埋深的增大，水平相对位移越来越小。结构在第一组地震波作用下层间相对位移值最小，第二组次之，第三组最大；三组地震波作用下，结构层间位移角均小于规范限值（4×10-3），满足抗震规范要求的弹性限值及弹塑性限值，表明车站结构整体抗震性能较好。

（3）通过两种抗震性能分析方法的数值模拟和验算，该车站结构总体满足抗震设防性能要求，抗震设计中应重点加强抗震构造措施。

［1］ 刘晶波，李彬.地铁地下结构抗震分析及设计中的几个关键问题［J］.土木工程学报，2006，39（6）：106.

［2］ 李雅.天津软土地区地铁车站结构抗震性能研究［D］.天津：天津城市建设学院，2012.

［3］ 李新星，陈鸿，陈正杰.地铁车站结构抗震设计方法的适用性研究［J］.土木工程学报，2014，47（2）：322.

［4］ 高智能，卓卫东，谷音.地铁地下结构抗震研究现状［J］.福州大学学报（自然科学版），2013，41（4）：599.

［5］ 宋磊，王涛，韦扣均，等.软土地区地铁车站抗震计算方法及分析［J］.地下空间与工程学报，2014，10（1）：1695.

［6］ 中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局.城市轨道交通结构抗震设计规范：GB 50909—2014［S］.北京：中国计划出版社，2014.

［7］ YOUSSRF M H，JEFFRAY J H.Seismic design and analysis of underground structures［J］.Tunneling and Underground Space Technology，2001，16（4）：247.

［8］ CHE A，IWATATE T.Shaking table test and numerical simulation of seismic response of subway structures［J］.Structures and Materials，2002，11（3）：367.