边载效应对浅层平板载荷试验影响研究

朱幸科，刘天云，林佑高

（1.中交第四航务工程勘察设计院有限公司，广东 广州 510230；2.中交第四航务工程局有限公司，广东 广州 510290）

浅层平板载荷试验（PLT）是广泛应用于土木工程的一种原位测试方法，适用于检测承压板下应力主要影响范围内地基土承载力特征值及变形参数。实际应用过程中一般将承压板放置在试坑中进行试验，加荷方式多采用反压施加。国内相关的规范、手册[1-2]对试坑尺寸和加荷方式均有详尽描述，国外的标准[3]对载荷试验的方法和要求也有所论述，然而对于承压板周围边载分布范围对试验结果的影响规律却鲜有文献涉及。本文基于Mohr-Coulomb模型，采用数值分析方法，结合具体工程实例，分析了承压板荷载位移曲线随边载范围变化规律，并进行了参数敏感性分析，对影响规律进行了总结，以期对工程实践具有一定参考价值。

1 问题提出

浅层平板载荷试验在实施时一般首先在场地开挖一试坑，清除表层扰动土。为保证承压板水平并与土层均匀接触，在承压板与土层接触处铺设厚度不超过20 mm中砂或粗砂找平层，然后放置承压板。承压板尽可能设置在试坑中间位置。试坑边缘覆土上方设置承压砂袋或枕木，砂袋上部设置大截面的型钢横梁以支撑上部荷载。出于安全考虑，两侧承压砂袋或枕木不宜过高，这也是承压板一般放置在试坑里进行试验的原因之一。此外，试坑尺寸过大同时会增大两侧承压砂袋之间距离，使得砂袋上方承受压载的型钢横梁过长，截面过大，安全风险也相应增加。因此工程实践中试坑尺寸经常难以达到规范要求。尤其对于大尺寸载荷板并且采用堆载方式施加反压，上述问题更为普遍。

对于密实砂土地基，上覆荷载作用足够大时，土体发生整体剪切破坏的可能性较大。Terzaghi对土体整体剪切破坏模型进行了修正[4-5]，将破坏区划分为5个，如图1，并给出了基底完全粗糙条件下土体极限承载力的一般表达式：

式中：Pu为土体的极限承载力，kPa；B为基础宽度，m；γ为土体重度，kN/m3；c为土体黏聚力，kPa；q 为基础边载，kPa；Nγ、Nc、Nq为基底承载力系数。

图1 土体整体剪切破坏模式Fig.1 The general shear failure mode of soil

由此可见，边载q的大小将影响到土体的极限承载力的确定。然而式（1）适用于土体达到极限承载力情况，并且假定从基础边缘即有覆土边载，无法直接应用此公式解释载荷试验周围覆土对试验结果的影响。

因此，承压板周围覆土边载范围对载荷试验成果的影响如何，是否会影响到对地基承载力的判定，已成为摆在工程技术人员面前一个亟待解决的问题。

2 工程案例

本工程为南亚一围海造陆项目，场地原状土层主要为砂层，回填料为中粗砂，厚度8~20 m。采用强夯工艺进行地基处理，以提高表层砂土地基的承载力。承载力检验采用浅层平板载荷试验，如图2所示。采用边长B=1.5 m方形承压板，试坑开挖尺寸3.0 m×3.0 m，深度0.35 m。砂土重度18 kN/m3，覆土边载q1=0.35×18=6.3 kPa，距离载荷板边缘0.75 m。试验采用上部堆载砂袋反压加载。两侧布设宽度0.6 m承压砂袋，砂袋纵向长度约5 m，距离坑边1 m，上边架设长约6 m型钢横梁，横梁上部砂袋堆载至700 kN后，启动千斤顶顶升型钢纵梁。上部堆载砂通过型钢横梁→型钢纵梁→千斤顶→承压板传力路径施加反力。

图2 平板载荷试验示意图（mm）Fig.2 Sketch of plate loading test(mm)

设计承载力为120 kPa，加载至240 kPa，约240×1.5×1.5=540 kN。此时试坑两侧承压砂袋处边载q2=（700-540）/2/（1×5）+6.3=22.3 kPa。

试验过程采用分级加载，每一级荷载沉降稳定后读取数据，加载过程试验结果如表1所示。

表1 载荷试验加载过程试验数据Table 1 Test data in process of PLT

加载过程试验曲线如图3所示。

图3 载荷试验加载过程P-S曲线Fig.3 P-S curve in loading process of PLT

从试验结果来看，P-S曲线总体处于线性阶段，加载到240 kPa，土体竖向总位移仅3 mm左右，可见土体仍处于线弹性变形阶段，并未达到极限破坏状态，不宜直接应用Terzaghi极限承载力理论对该问题进行分析。

以下将通过数值分析方法结合现场原位测试荷载位移曲线进行讨论分析。

3 数值分析

3.1 计算模型

采用有限元软件Plaxis模拟载荷试验工况，采用二维轴对称模型，土体采用Mohr-Coulomb模型，承压板采用弹性板模型。因现场试验采用边长1.5 m的方形承压板，须按照面积等效原则转化为圆形板。

式中：D为圆形承压板等效直径，m；B为方形承压板边长，m。

为分析边载效应对试验结果的影响，分别建立模型1和模型2。模型1为无边载条件下载荷试验模型。模型2为有边载条件下载荷试验模型，覆土边载距离承压板边缘x=0.75 m。

为便于分析，另外增加x=0.00 m、1.15 m两种工况，以反映覆土边载距离的影响。定义承压板中心点A，以得到承压板的位移随荷载变化规律。

对于轴对称模型可采用半无限空间分析，模型尺寸5 m×10 m，如图4所示。采用三角形网格进行剖分，模型两侧边界设置水平约束，顶部自由边界，底部为固定约束。

图4 浅层平板载荷试验数值分析模型（mm）Fig.4 Numerical analysis model for PLT（mm）

3.2 参数取值

为保证参数取值的合理性，同时更客观地反映数值分析结果与现场载荷试验的对比结果，土体的变形模量E0，内摩擦角φ，侧向土压力系数K0等主要模型输入参数将不首先考虑通过现场PLT结果进行推算，而是根据试验场地CPT测试结果进行反推。

3.2.1 变形模量

对于强夯处理过的超固结土，压缩模量M0可以通过式（3）进行推算[6]：

式中：qc为锥尖阻力，MPa。

根据现场载荷试验区附近CPT测试结果，处理后表层砂土的qc平均值为21 MPa。因此砂土的压缩模量M0=5×21=105 MPa。变形模量可以通过式（4）求得：

式中：ν为土体泊松比，对于砂土取ν=0.3。计算可得变形模量：E0=78 MPa。

3.2.2 内摩擦角

内摩擦角φ可以通过式（5）推算[5]：

因此，内摩擦角φ=33.6°。

3.2.3 水平侧压力系数

超固结土的水平侧压力系数K0可以通过式（6）推算[6]：

式中：K0（nc）为相应于正常固结土的水平侧压力系数；OCR为超固结比。根据式（5）计算结果得出：

式中：对于砂土地基 qt≈qc=21 MPa；σv0′=3×18=54 kPa；对于非胶结砂m≈0.72；Pa为大气压力，Pa=100 kPa。

因此，K0=K0（nc）OCR（1-sinφ）=1.14。

土层和承压板的模型输入参数见表2。

表2 土层和载荷板参数Table 2 Parameters for soil and loading plate

3.3 计算分析

分别针对边载距离承压板x=0.00 m、0.75 m、1.15 m进行计算，其他参数参见表2。模型1与模型2计算结果如表3所示。

表3 模型1和模型2计算结果Table 3 Calculation results of Model 1 and Model 2

图5为荷载工况5条件下边载距离承压板0.75 m时土体的总应力云图，可以看出，边载作用下土体中的应力分布对承压板下部土体的应力区是有影响的。

图5 地基土总应力云图Fig.5 Total stress diagram for foundation soil

结合现场原位测试曲线，可以得到数值分析与现场载荷试验P-S曲线的对比结果，参见图6。

图6 数值分析与现场PLT结果P-S曲线对比Fig.6 Comparation of numerical analysis with in-situ PLT in P-S curve

可以看出，对于模型2，有边载条件下，随着边载与承压板距离的增大，承压板沉降值从4.9 mm逐渐增大到5.3 mm，趋近于无边载情况下的位移5.5 mm。然而沉降变化幅度并不大，考虑为强夯处理后的砂土地基为超固结土，变形模量较大，抵抗变形能力强，边载对承压板下部土体变形的影响并不大。相对于现场载荷试验P-S曲线，数值计算结果偏大，表明场地地基土经强夯处理后实际的变形模量要大得多，但沉降计算值与现场实测值仍在同等数量级范围以内。

由于土体荷载位移曲线总体上仍处于线性变化阶段，土体并未达到极限承载力状态。根据JGJ 79—2012《建筑地基处理技术规范》对于处理后地基承载力特征值确定方法，由现场原位测试及数值模拟P-S曲线均可以判断地基土已经满足设计承载力特征值120 kPa。可见边载效应并未影响到对土体是否满足设计承载力的判断。考虑到模型输入参数取值对数值分析结果可能有影响，下面对主要模型输入参数进行敏感性分析。

3.4 参数敏感性分析

3.4.1 变形模量

模型计算时变形模量首先考虑采用试验场地CPT测试结果进行反推，作为对比分析，下面将通过PLT结果反算。

变形模量E0可以通过式（9）进行计算[2]：

式中：I0为载荷板形状系数， 对于圆形板取0.785，对于方形板取0.886；υ为土的泊松比，对于砂土取υ=0.3；p为P-S曲线线性段压力，kPa，本次计算采用p=120 kPa；d为载荷板边长，d=1.5 m；s为与p对应的沉降，s=1.39 mm，参见表1。

因此变形模量E0=104.4 MPa。

变形模量采用104.4 MPa，其他参数参照表2，计算结果如图7所示。

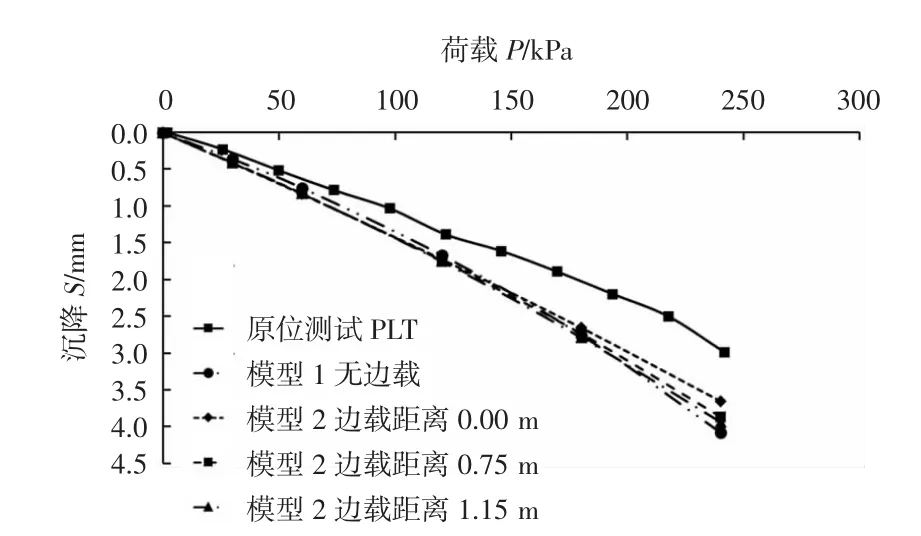
图7 数值分析与现场PLT结果P-S曲线对比（E0=104.4 MPa）Fig.7 Comparation of numerical analysis with in-situ PLT in P-S curve(E0=104.4 MPa)

可见增大土体变形模量后，数值分析结果显示承压板竖向位移值减小，较原来计算值减小1.5~2 mm左右。此时P-S曲线与现场PLT结果更为接近。

3.4.2 土体抗剪强度指标

对于密实状态的中粗砂，其最大内摩擦角可达到40°[2]，作为参数敏感性分析，计算内摩擦角采用40°，其他参数仍参照表2，计算结果如图8所示。

图8 数值分析与现场PLT结果P-S曲线对比（内摩擦角40°）Fig.8 Comparation of numerical analysis with in-situ PLT in P-S curve(Internal friction angle φ=40°)

可以看出，土层内摩擦角增大后，土体的抗剪强度增大，承压板下土体总体位移略有减小，然而并不明显，同时边载与承压板距离变化对P-S曲线的影响更小。

3.4.3 超固结比

本工程现场试验场地地基土层为强夯处理后的砂土地基，考虑为超固结土，计算得到水平侧压力系数K0=1.14。作为对比分析，假设为正常固结土，根据式（7），K0可取0.45。

K0取0.45，其他参数参照表2，计算得到PS曲线如图9所示。

图9 数值分析与现场PLT结果P-S曲线对比（K0=0.45）Fig.9 Comparation of numerical analysis with in-situ PLT in P-S curve(K0=0.45)

可见对于正常固结土，边载效应对载荷试验结果的影响相对于超固结土较为明显。K0对土体的初始应力状态影响较大，对于超固结土，土体水平侧压力系数K0越大，相应初始水平应力也越大，抵抗边载引起土体变形的能力也越强。

通过对模型主要输入参数进行敏感性分析，可见土体的变形模量和抗剪强度指标对数值模拟分析结果影响并不明显，土体侧压力系数K0的影响相对较为明显。

4 结语

1）本文从数值计算角度分析了工程中浅层平板载荷试验在开挖试坑较浅情况下，试坑尺寸大小亦即覆土边载范围对浅层平板载荷试验结果的影响规律。计算表明，浅层平板载荷试验承压板周围覆土边载对试验结果P-S曲线的影响随着边载与承压板距离的增大而减小，对于处理后砂土地基总体影响较小。

2） 对于处理后砂土地基，可认为是超固结土，试验过程地基土总体仍处于线弹性状态，未达到极限破坏状态，覆土边载虽然对试验结果有所影响，但是根据规范中对土体承载力特征值确定方法，覆土边载并未影响到工程中对于土体是否满足设计承载力要求的判断。

3） 土体的变形模量E0，内摩擦角φ参数取值对数值分析结果影响较小，土体侧压力系数K0直接影响到土体的初始应力状态，对结果影响较大。对于超固结砂土地基K0值较大，土体初始水平应力较大，抵抗变形的能力也较强，相应覆土边载对试验结果影响也较小。

4）本文仅针对试坑开挖较浅，且为处理后砂土地基条件下讨论分析了覆土边载对浅层平板载荷试验结果的影响程度和规律，对于黏性土地基以及试坑较深工况下覆土边载的影响如何，值得下一步进行深入研究分析。

参考文献：

[1] JGJ 79—2012.建筑地基处理技术规范[S].JGJ 79—2012,Technical code for ground treatment of buildings[S].

[2]《工程地质手册》编委会.工程地质手册[M].4版.北京：中国建筑工业出版社，2006.Handbook of Engineering Geology editorial board.Handbook of engineeringgeology[M].4thed.Beijing:ChinaArchitecture&BuildingPress,2006.

[3] BS 1377-9:1990,Methods of test for soils for civil engineering purposes-Part 9:In-situ tests[S].

[4] 陈仲颐，周景星，王洪瑾.土力学[M].北京：清华大学出版社，2007.CHEN Zhong-yi,ZHOU Jing-xing,WANG Hong-jin.Soil mechanics[M].Beijing:Tsinghua University Press,2007.

[5] BOWLES Joseph E.Foundation analysis and design[M].5th ed.New York:The McGraw Hill Companies,1997.

[6]LUNNE Tom,ROBERTSON Peter K,POWELL John M.Cone penetration testing in geotechnical practice[M].London:Spon Press,2002.