MSK调制下的匹配滤波接受研究∗

2018-04-27陈鲁聪

舰船电子工程 2018年4期

胥艳陈鲁聪

（1.中国人民解放军91208部队青岛 266000）（2.海军航空大学烟台 264001）

1 引言

现代战争中保证通信的畅通是赢得战争胜利的关键。在信噪比相同的情况下，接收机输出误码率是衡量其性能好坏的标志［1］。匹配滤波接收机是一种最佳接收机，它将最小误码率作为接收的准则，这种接收机能使含噪信号中有用成分的信号能量聚集，使得输出幅度达到峰值［2～3］，尤其是在对抗高斯白噪声方面，将使得抽样时刻上的输出信噪比最大，从而保证解调输出的误码率最小。这种最佳接收机广泛应用于军事通信、导航、雷达，尤其是电台信号接收方面。随着匹配滤波和相关硬件技术的日趋成熟，它在军事领域运用也越来越广泛，因此对其在各种数字通信方式、不同信道下的性能分析和研究，具有重要的军事价值和意义［4］。

最小频移键控（MSK）是2FSK的改进［5］。2FSK体制虽然性能优良、易于实现，并得到了广泛的应用，但是它也有一些不足之处。首先，它占用的频带宽度比2PSK大，其频带利用率比较低。其次，若使用开关法产生2FSK信号，则相邻的码元波形的相位可能不连续，因此在通过带通特性的电路后由于通频带的限制，使得信号波形的包络产生较大的起伏。此外，2FSK信号的两种码元波形不一定严格正交，而如果严格正交将会使得误码率性能更好［6］。

本文利用MSK调制和匹配滤波的相关接受的优越性，进一步研究了匹配滤波接受的方法，研究了MSK在匹配滤波下的解调性能。

2MSK调制原理

最小频移键（MSK）控源于频率键控。首先，频率键控占用的频带宽度比2PSK大，频带利用率较低。其次，2FSK信号相位在很多时候都不是连续的，所以通过带通特性的系统后由于通频带的限制，使得信号波形的包络产生较大的起伏。

为克服上述缺点，对于2FSK信号做了改进，发展出MSK信号。MSK信号是一种包罗恒定、相位连续、带宽最小并且严格正交的最小频移键控信号［7～8］。MSK信号可以用两个正交的分量表示：

式（1）中右端第1项为同向分量，其载波为cоsωct；第2项称正交分量，其载波为 sinωct，pk与qk是基带码元经过差分编码、串/并转换后的输出码元。根据上式构成的方框图如图1所示。

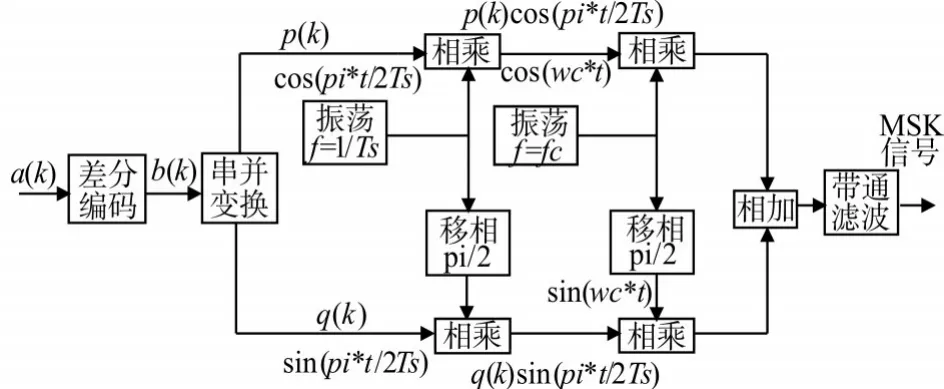
图1 MSK调制图

图1中输入数据序列为ak，它经过差分编码后变成序列bk，差分编码起就是DPSK调制中采用的码变换器（双稳触发器）。比如，输入码元序列为

它经过此差分编码器后得到输出序列：

序列bk经过串/并变换，分成pk支路和qk支路，bk的码元交替变成上下支路的码元，即有

串/并变换输出的支路码元长度为输入码元长度的2倍，即2Ts，若仍然采用原来的序列号k，将支路第k个码元长度仍当作为Ts，则可以写成：

即pk支路的码元为：p1，p2，p3，p4···=b1，b1，b2，b2，b3，b3，b4，b4···，qk支路的码元为：q1，q2，q3，q4···=b0，b2，b2，b4，b4，b6，b6···，这里的pk和qk的长度仍然是原来的Ts也就是说，因为p1=p2=b1，所以由p1和p2构成一个长度等于2Ts的取值为b1的码元。

这两条支路数据pk和qk再经过两次相乘，就能合成MSK信号了。

3 高斯白噪声下的匹配滤波原理

错误概率最小是作为最佳接受的准则。在本节中，将讨论线性滤波器对信号滤波时，如何使抽样时刻上线性滤波器的输出信噪比最大。当然这种使输出信噪比最大的线性滤波器就称为匹配滤波器［9～11］。

设接收滤波器的传输函数为H(f)，冲激函数为h(t)，滤波器输出码元s(t)的持续时间为Ts，信号和噪声之和r(t)为

式中：s(t)为信号码元；n(t)为高斯白噪声。

并设信号码元s(t)的频谱密度函数为S(f)，噪声n(t)的双边带功率谱密度为为噪声单边带功率谱密度。

由于假定滤波器是线性的，根据线性电路叠加定理，当滤波器输入电压r(t)中包含信号和噪声两部分时，滤波器的输出电压y(t)中也包含相应的输出信号s0(t)和输出噪声n0(t)两部分，即

其中

为了求出噪声功率，由式（9）：

可知，一个随机过程通过线性系统时，其输出功率谱密度PY(f)等于输入功率谱密度PR(f)乘上系统传输函数H(f)的模的平方。故而，这时的输出噪声功率N0为

因此，在抽样时刻t0上，输出信号瞬时功率与噪声的平均功率之比为

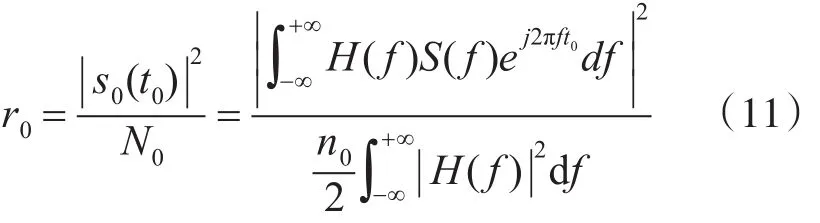
为了求出r0的最大值，可以利用施瓦兹（Schwarz）不等式：

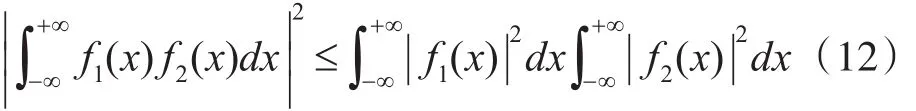
将式（11）右端的分子看作是式（12）的左端，并令

则有

而且当

由式（16）可见，匹配滤波器的冲击响应h(t)就是信号s(t)的镜像s(-t)，但从时间轴上（向右）平移了t0在图2中画出了从s(t)得到h(t)的图解过程。

图2 从s(t)得到h(t)的变换过程图解

一个实际的匹配滤波器应该是物理可实现的，其冲激响应符合因果关系，在输入冲击脉冲加入前不应该有冲激响应出现，即必须有

式（19）的条件说明，接收滤波器输入端的信号码元s(t)在抽样时刻t0之后必须为零。而且一般不希望在码元结束之后很久才抽样，故通常选择在码元末尾抽样，即选t0=Ts故匹配滤波器的冲激响应可以写为

这时，若匹配滤波器的输入电压为s(t)，则输出信号码元的波形，可以求出：

式（21）表明，匹配滤波器输出信号码元波形是输入码元波形的自相关函数的k倍，k是一个任意常数，它与r0的最大值无关；通常取k=1。

上述推导过程都是基于输出信噪比最大，误码率最小这一目的。导出了匹配滤波器的系统函数为，且其有最大输出信噪比

4 MSK调制信号的匹配滤波解调

在MSK信号中，由于波形的频率间隔很小，采用与FSK一样的匹配滤波方式，码元之间的将相互干扰，MSK信号具有相位连续、包络恒定的特点［12～15］，使得采用传统的匹配滤波方式，无法真正相位匹配，最终性能更差，所以必须从MSK调制的原理出发，在解调时，将I、Q支路分开，分别滤去载波后，单独进行匹配滤波处理，解调出I、Q支路的码元，最后经并/串转换、差分解码处理，实现解调。其匹配滤波解调流程图如图3所示。

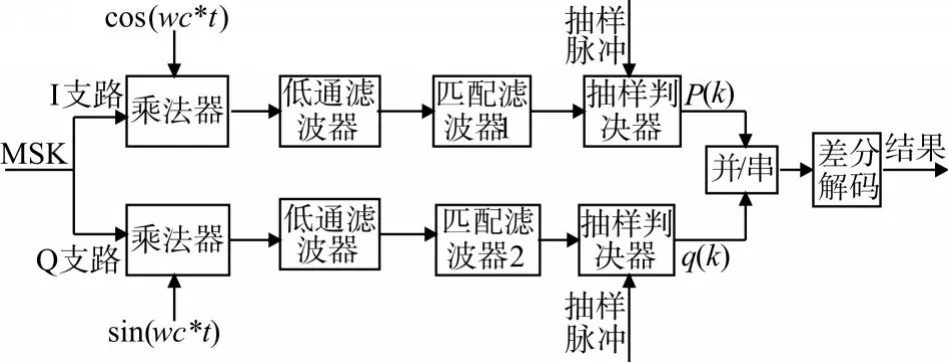
图3 MSK匹配滤波解调流程图

5 仿真分析

5.1 MSK信号调制与解调

在匹配滤波条件下，对MSK信号的解调仿真，在理想条件下即无噪声条件下，对图3进行检验，对比解调结果和基带信号，看图3的解调流程是否合理。

无噪声条件下，MSK信号的匹配滤波解调仿真

首先假定所要传输的基带信号的个数为10，分别为1，0，1，0，1，0，1，0，1，0，fc=25Hz。得到基带信号的MSK调制波形如图4所示。

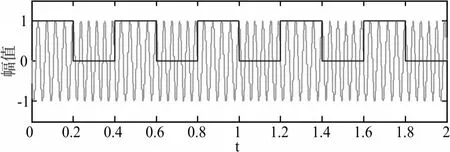
图4 MSK信号调制

将调制好的MSK信号加入图3的流程中，经过匹配滤波器1和匹配滤波器2分别得到I、Q支路的输出波形，分别如图5和图6所示。

图5 I支路匹配滤波器1输出波形

图6 Q支路匹配滤波器2输出波形

按照图3 MSK信号匹配滤波解调的流程，将匹配滤波器1与匹配滤波器2的输出波形在固定的抽样时刻进行抽样，将抽样值与零比较，从而确定出I、Q两支路的码元的信息。将I、Q支路的码元经并/串转换、差分解码处理，就得到了基带码元。通过仿真，得到了解调结果如图7所示。

图7 MSK信号匹配滤波解调后的结果

比较基带信号与解调结果，发现两者是一致的，说明了图3 MSK匹配滤波解调流程也是是正确的、可行的。

5.2 MSK匹配滤波下的容错性能分析

在非理想条件下即存在高斯白噪声的条件下，通过图3的解调方式对MSK信号进行解调，统计在不同信噪比的条件下，解调信号的误码率，并利用统计的数据绘出解调结果的误码率曲线。

首先假定需要传输的码元个数为100000，在MSK调制信号中加入信噪比大小从-4db到11db间隔1变化的高斯白噪声，利用图3的解调数据流程进行解调。统计的在不同信噪比下，对应的误码率，从而绘出误码率曲线，如图8所示。由图8可知，匹配滤波下的MSK调制解调的性能较好，在较低的信噪比的条件下，其解调的误码率较低。

图8 MSK匹配滤波解调性能

5.3 不同调制方式的比较

为方便比较ASK、FSK、PSK、MSK调制信号在匹配滤波接收下的性能，将四者的误码率曲线绘于同一坐标系中，如图9所示。

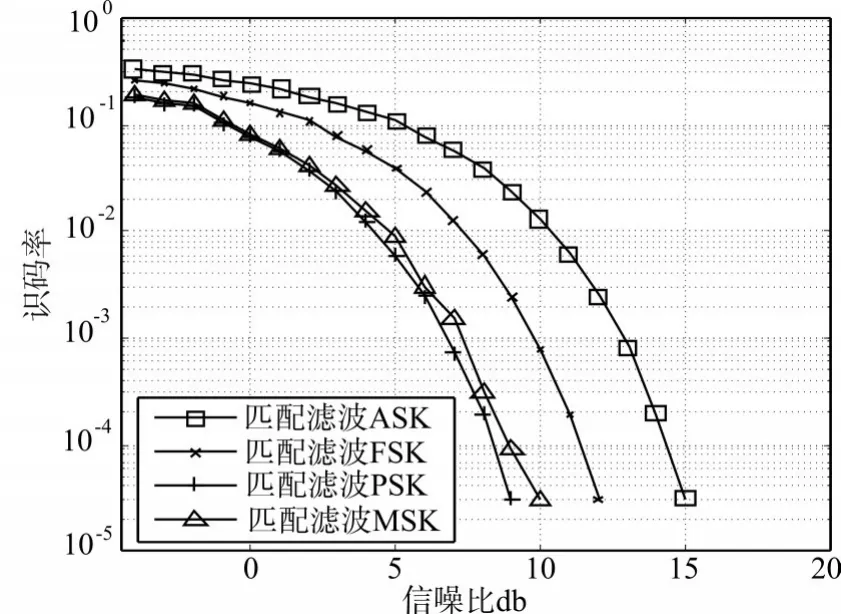
图9 ASK、FSK、PSK、MSK匹配滤波接收误码率曲线

从图9可看出PSK的性能最好，其次是MSK，再次是FSK，ASK的性能相比较其它而言是最差的，采用图9的匹配滤波方式，MSK的性能比较接近PSK的性能。

6 结语

通过推导MSK调制与匹配滤波器的一般表达式，在此基础上对MSK分别进行匹配滤波处理，再在特定点上抽样判决，实现了正确的解调。同时，对每一种调制信号做了性能分析，画出了误码率曲线。MSK调制的匹配滤波解调性能较好，同时与其他调制方式进行比较，可知MSK调制方式好于ASK、FSK性能，同时接近于PSK。

［1］樊昌信，曹丽娜.通信原理［M］.北京：国防工业出版社，2012：180-205，241-247，311-319.

［2］陈宏宇，沈学民，朱振才.基于匹配滤波的静态红外地平仪信息处理方法［J］.红外与毫米波学报，2007，26（3）：191-195.

［3］胡茂凯，陈西宏，张群.基于匹配滤波的正交频分复用信号识别［J］.吉林大学学报（工学版），2012，42（6）：1581-1586.

［4］宋晓琳，张三林，张伟伟.应用匹配滤波器的车载线恒虚警率识别方法［J］.电子测量与仪器学报，2015（3）：328-336.

［5］付贞，温东，姜波.甚低频天电噪声中的MSK通信系统仿真［J］.舰船电子工程，2010，30（1）：98.

［6］岳光荣，刘志特，杨国胜等.水下甚低频MSK信号最大似然多符号差分解调算法［J］.电子科技大学学报，2016，45（4）：528-532.

［7］赵辉，赵旦峰，候长波等.MSK调制解调器的设计与实现［J］.哈尔滨理工大学学报，2011，16（1）：102-106.

［8］周世阳，王赏，程郁凡.MSK信号的最大似然非相干检测算法研究［J］. 信号处理，2016，32（7）：866-871.

［9］吴迪军，徐振海，张亮等.极化空时自适应匹配滤波检测器［J］.电子学报，2013，38（6）：93-96.

［10］李海，刘新龙，周盟等.基于修正自适应匹配滤波器机动目标检测方法［J］.雷达学报，2015，4（5）：552-559.

［11］王培峰，陈高峰，华铁均等.基于二元纯相位匹配滤波的光电混合模式识别［J］.红外与毫米波学报，2000，19（2）：117-120.

［12］王文娟，李绪凯，张天辉.GMSK调制解调方法及误码率分析［J］. 中国科技信息，2016（3）：50-53.