基于SOGI和FLL的感应电机磁链观测器设计

张 红，何小敏

(1.广州铁路职业技术学院，广州 510430；2.广东工业大学，广州 510006)

0 引 言

高性能感应电机驱动系统需要有准确的磁链估计。磁链估计可以通过不同方式实现，最广泛使用的方法是基于电压模型，对电机反电动势进行积分获取，磁链估计避免了转速传感器的使用，有利于系统可靠性的提高[1-3]。

纯积分器有3个主要问题，一是传感器和模数转换器引入的直流偏置将容易导致积分器饱和[4-5]；二是由积分初始条件引起的，若初始条件不准确，则可能导致积分器输出直流偏置，然而这种偏移实际上并不存在；第三个问题与谐波有关，应该尽量避免估计磁链中的谐波[6]。故实际中通常由低通滤波器来代替纯积分器[7-8]。虽然低通滤波器可解决前述问题，但当电机工作频率点接近或低于滤波器截止频率时，将引入幅值和相角误差到估计量中[9]。这意味着难以在全转速范围内选择到合适的截止频率，只能在幅值和相角误差之间折衷。文献[10-11]设计了截止频率可编程低通滤波器方案，文献[12-13]将截止频率可编程方案进一步修改为三级和五级低通滤波器级联结合高通滤波器的方案，截止频率可编程技术依赖于估计的同步角频率，而同步角频率是通过对电机位置角求微分计算得到的，但是微分也会引入额外的问题，例如微分器放大后的噪声干扰。

综上所述，无论是传统纯积分器或低通滤波器方案，亦或是截止频率可编程级联低通滤波器方案都未全面解决精确磁链估计问题。为此，本文在前述文献研究基础上，设计了一种基于SOGI和FLL的新型磁链观测器方案，并通过实验对其磁链估计性能进行了验证。

1 磁链估计中的积分问题

图1为感应电机(以下简称IM)的经典磁场定向矢量控制和直接转矩控制系统框图。

(a) 磁场定向矢量控制

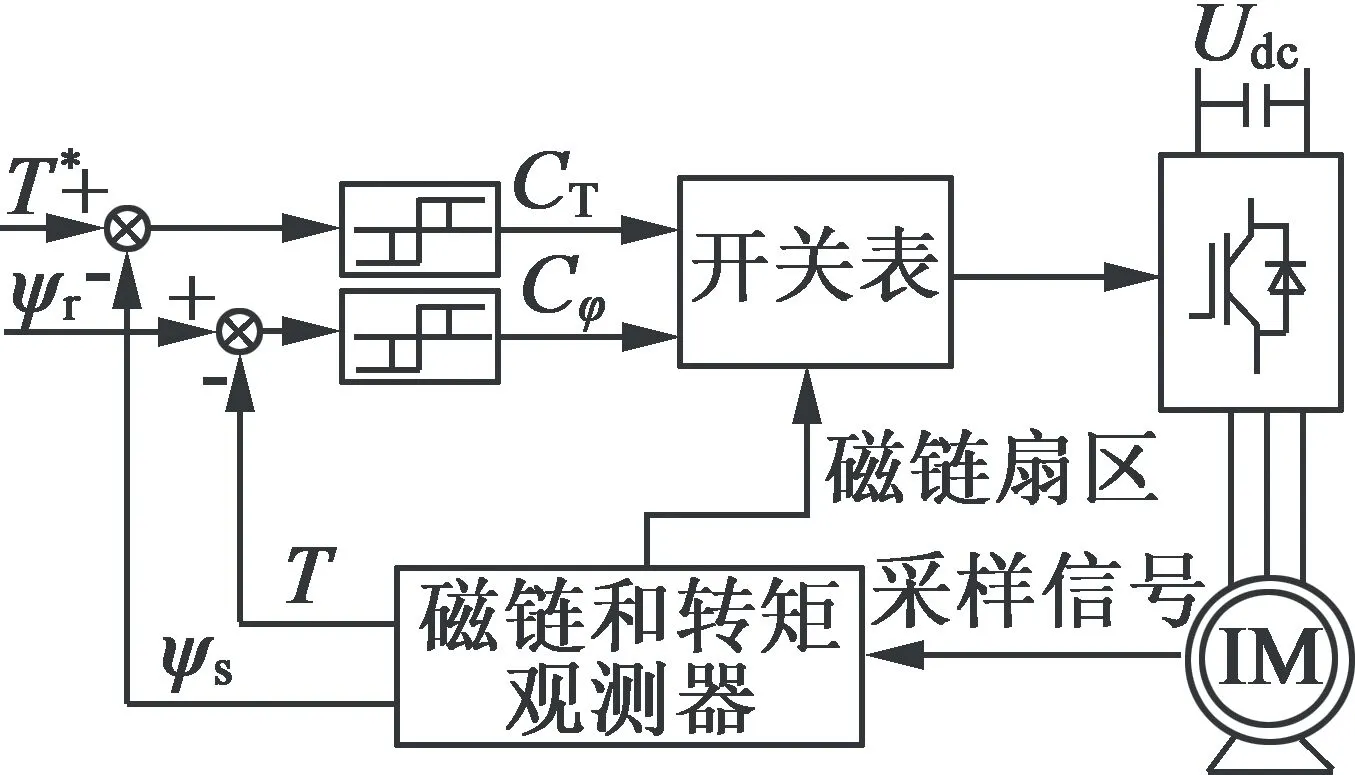
(b) 直接转矩控制

在静态参考系中，给出基于电压模型的定子和转子磁链的估计式如下：

(1)

(2)

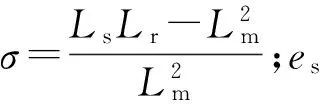
(3)

1.1 实际反电动势信号

从式(3)可以看出，反电动势esα包含定子电压usα和定子电阻上压降Rsisα2个分量，isα可由电流传感器测量得到，故电流传感器、运算放大器和模数转换器的偏差都可能导致直流偏置[4-5]。

实际上，基于直流电压Udc和变频器占空比Da,Db和Dc可得到定子电压如下：

(4)

(5)

进而得到α-β参考系中的定子电压：

usα=usa

(6)

(7)

事实上，若无过调制，则式(4)～式(7)所描述的定子电压是电流控制器的输出，而由于电流测量中存在的直流偏置和谐波将导致电流控制器输出存在直流或谐波分量，故实际电机反电动势中存在直流偏置和谐波分量。从而更精确的电机反电动势表达式如下：

(8)

式中：A0是直流偏置;A1sin(ω1t+φ01)是基波分量；Ahsin(ωht+φ0h)为第h次谐波分量。将拉普拉斯变换应用于esα，有：

(9)

1.2 基于纯积分器的磁链估计

如果磁链观测器由纯积分器实现，则式(3)的拉普拉斯变换：

(10)

式中：Ψsα_I(s)为ψsα_I的拉普拉斯变换。将式(9)代入式(10)，并应用拉普拉斯反变换可得：

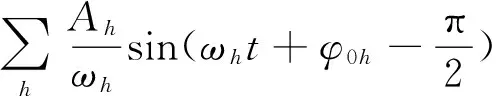
(11)

从式(11)中可以看出，直流偏置项A0t意味着随着时间推移，将出现积分器饱和，且无关A0的大小。同时还可以看出，不同积分初始条件也将导致不同的积分器输出直流偏置，将进一步影响到控制器的正确计算。另外，式(8)中每个正弦电压反映到式(11)中都有相对应的正弦磁链，其幅值为电压幅值除以其角频率。因此，在电机高速下的磁链估计误差衰减较大，可以忽略；而电机低速时，分母中的角频率ωh较小，电压幅值Ah则可能变得非常大，从而不能忽略。总之，在式(11)的纯积分器输出项中，只有基频正弦波应保留作为磁链估计的有效量，其余4项都是由于传感器或硬件电路缺陷导致的，与实际磁链无关，故纯积分器方案难以在工程中实际使用。

1.3 基于低通滤波器的磁链估计

纯积分器的一个较好替代方案是一阶低通滤波器。首先，式(10)变为：

(12)

式中：Ψsα_F(s)为一阶低通滤波器估计的ψsα_F的拉普拉斯变换，截止频率ωc通常设置得远低于ω1。将式(9)代入到式(12)，并应用拉普拉斯反变换可得：

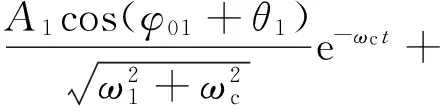
(13)

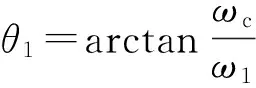
2 基于SOGI和FLL的新型磁链估计方案

基于纯积分器和低通滤波器的磁链估计存在着固有缺陷，本文设计了一种新型磁链估计方案，下面将从原理开始逐步深入到具体的设计。

2.1 二阶广义积分器(以下简称SOGI)

SOGI广泛用于电网电压不平衡条件下的正序分量提取[14-15]。SOGI的基本原理和结构如图2所示。图2中k为阻尼因子，ω′为调谐频率，v为输入，v′为输出，输出和输入的误差为εv=v-v′，q_v′为另一个被提取的正交正弦分量，v′和q_v′可用于计算输入v的幅值和相位，在q_v′之前，还可提取第三个正弦分量i_v′，其相位滞后v为90°，幅值等于输入v的幅值除以其频率，若v为正弦，则i_v′为v的积分。

图2 二阶广义积分器的结构框图

2.2 单级SOGI磁链估计器

根据图2中的i_v′和v的关系，可使用单级SOGI来执行积分来获得磁链估计。图3为单级SOGI磁链估计器的结构框图。

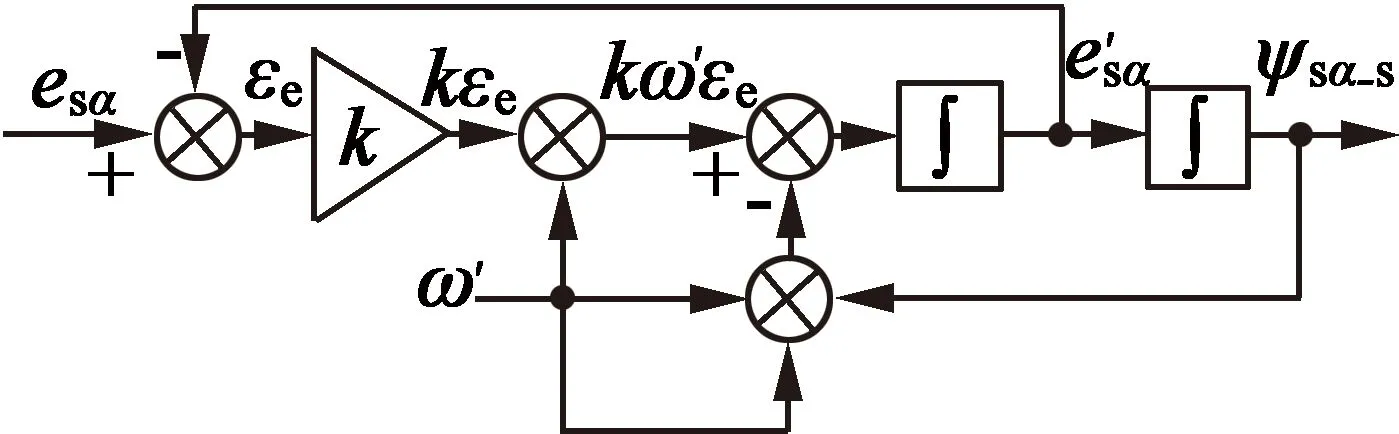
图3 单级SOGI磁链估计器框图

根据图3中结构，可推导出估计磁链Ψsα_S(s)的传递函数：

(14)

(15)

将式(9)代入式(14)，并进行拉普拉斯反变换可得：

(16)

式中：ψsα_S为时域下的估计磁链，其中f0(t)，f1(t)和fh(t)是暂态偏置，与直流量、基波和谐波初值相关，在稳态下将衰减到零。在式(16)中，还有由SOGI引起的基波和谐波相位误差γ1和γh，具体的表达式如下：

(17)

(18)

在稳态下，如果精确知道基频或ω′=ω1，则式(16)变为：

(19)

对比式(19)、式(11)和式(13)可看出，单级SOGI磁链估计器不会由直流漂移而引起饱和，但仍存在与ω1成反比的输出直流偏置。此外，只要精确测到ω1，估计的基频磁链就没有幅值和相位的误差，从而可以避免幅值和相位补偿算法，这显著优于低通滤波器方案,但从式(19)中还可以看出，单级SOGI仍能检测到谐波磁链。

2.3 基于单级SOGI和FLL的磁链估计器

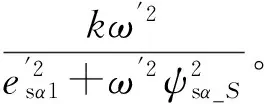
(20)

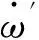
(21)

从图4和式(20)可以看出，ψsα_S中的任何直流和谐波分量将影响到εf，这将导致频率和磁链估计误差，特别是在电机低速时。因此，磁链估计中的直流和谐波分量必须进一步衰减，以确保估计的精度。下一步考虑引入多级SOGI解决这个问题。

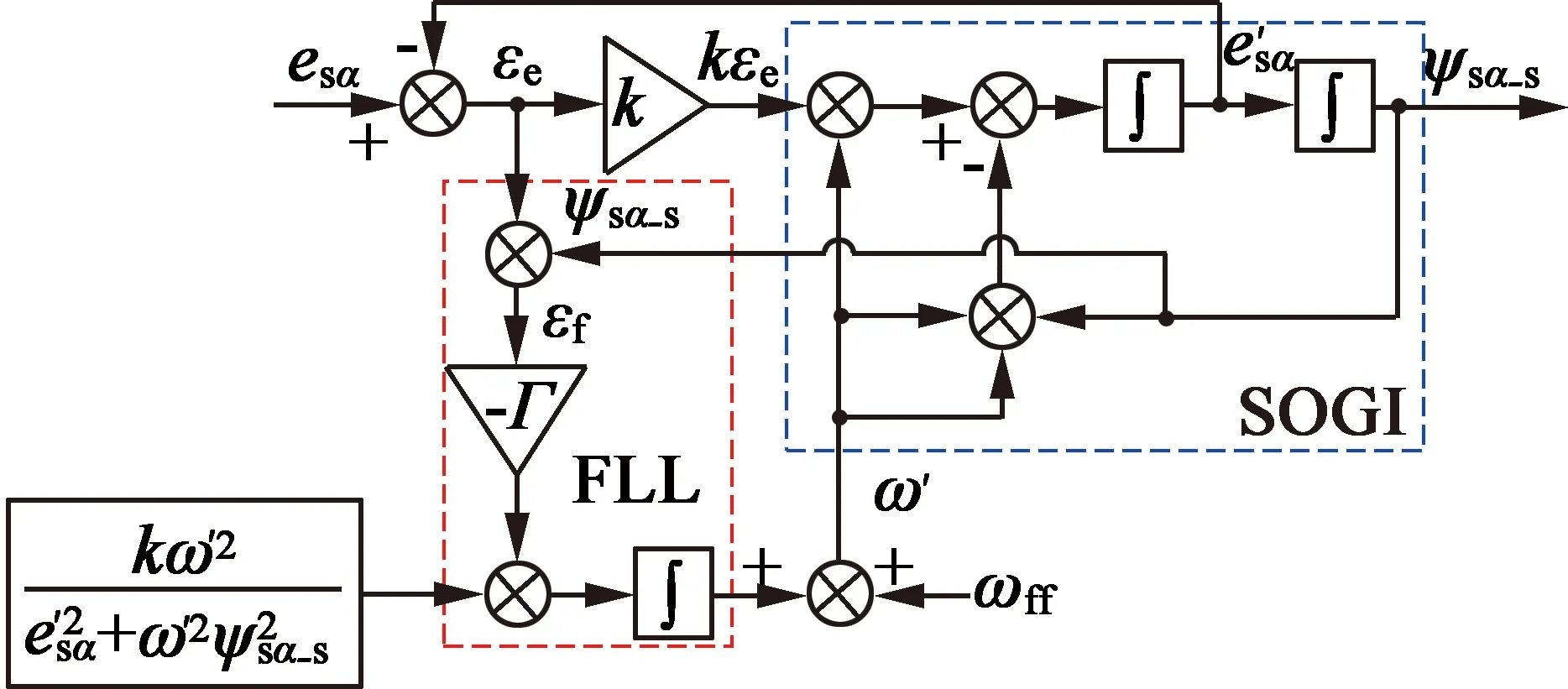
图4 基于单级SOGI和FLL的磁链估计器框图

2.4 基于多级SOGI和FLL的磁链估计器

对图4中基于单级SOGI和FLL的磁链估计器进行改进，引入多级SOGI后可得如图5所示的新型磁链估计器。

对于h=0，SOGI将退行为一个积分器。图5的框图被分为3个部分，其中前2个部分用于基频磁链估计和FLL实现，第三个部分用于磁链估计中的直流和谐波衰减。为了进一步分析新型磁链估计器的性能，对第h重SOGI进行传递函数的推导如下：

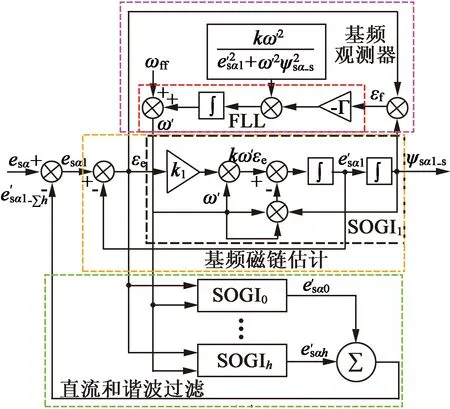
图5 基于多级SOGI和FLL的磁链估计器框图

(22)

图6 SOGIh模块

对于h≥1，SOGIh模块的增益参数kh必须相同，从而具有相同的带宽，即kh=k(h≥1)。数学上，对于k和k0有如下约束关系：

(23)

式(23)可以作为实际中参数选择的依据。从图5中还可以看出，系统误差和输入反电动势之间的第二个传递函数N(s)：

(24)

式中：Bh(s)的表达式如式(22)所示。将式(22)乘以式(24)可以得到：

(25)

式(25)为所提取的反电动势第h次谐波和输入反电动势的传递函数Mh(s)。类似地，可以得到反电动势基波和输入反电动势的传递函数A(s)：

(26)

对所有h≥0，将s=jhω′代入后，可观察到直流分量和谐波的幅值增益变为0，而基波增益是一致的。故式(26)中A(s)即是阻断直流和谐波的陷波滤波器，也是针对反电动势基波的带通滤波器。最后，从图5中可以看出，ψsα1_S和提取的基频分量esα1之间的传递函数可写为：

(27)

对比式(15)和式(27)可发现，两式中的传递函数形式一致，区别在于式(15)中esα被式(27)中的esα1取代。这进一步说明了基于多级SOGI和FLL的磁链估计器和单级SOGI磁链估计器的形式相同，但是输出的估计磁链在稳态下没有直流分量和谐波项。从而有：

(28)

3 实验验证

图7为所搭建的IM传动控制系统实验平台，基于平台可以对所设计的新型磁链观测器进行试验研究。实验平台所使用的IM额定功率为11 kW，同时设置一台功率接近的永磁同步电机作为负载，两者通过齿轮箱减速器联接到一起，其中IM的主要参数如表1所示。图8为IM驱动控制器设计框图。从图7中可以看出，控制器核心芯片采用德州仪器DSP(TMS320F2812)实现，电机转速采用一个增量式编码器采集，变频器开关频率设置为19.2 kHz，死区时间为1.5 μs。此外，基于多级SOGI和FLL的新型磁链估计器中参数设置包括SOGI0的增益k0为0.166 8，SOGIh(h≥1)的增益kh为0.166 8，FLL的增益Γ为30。

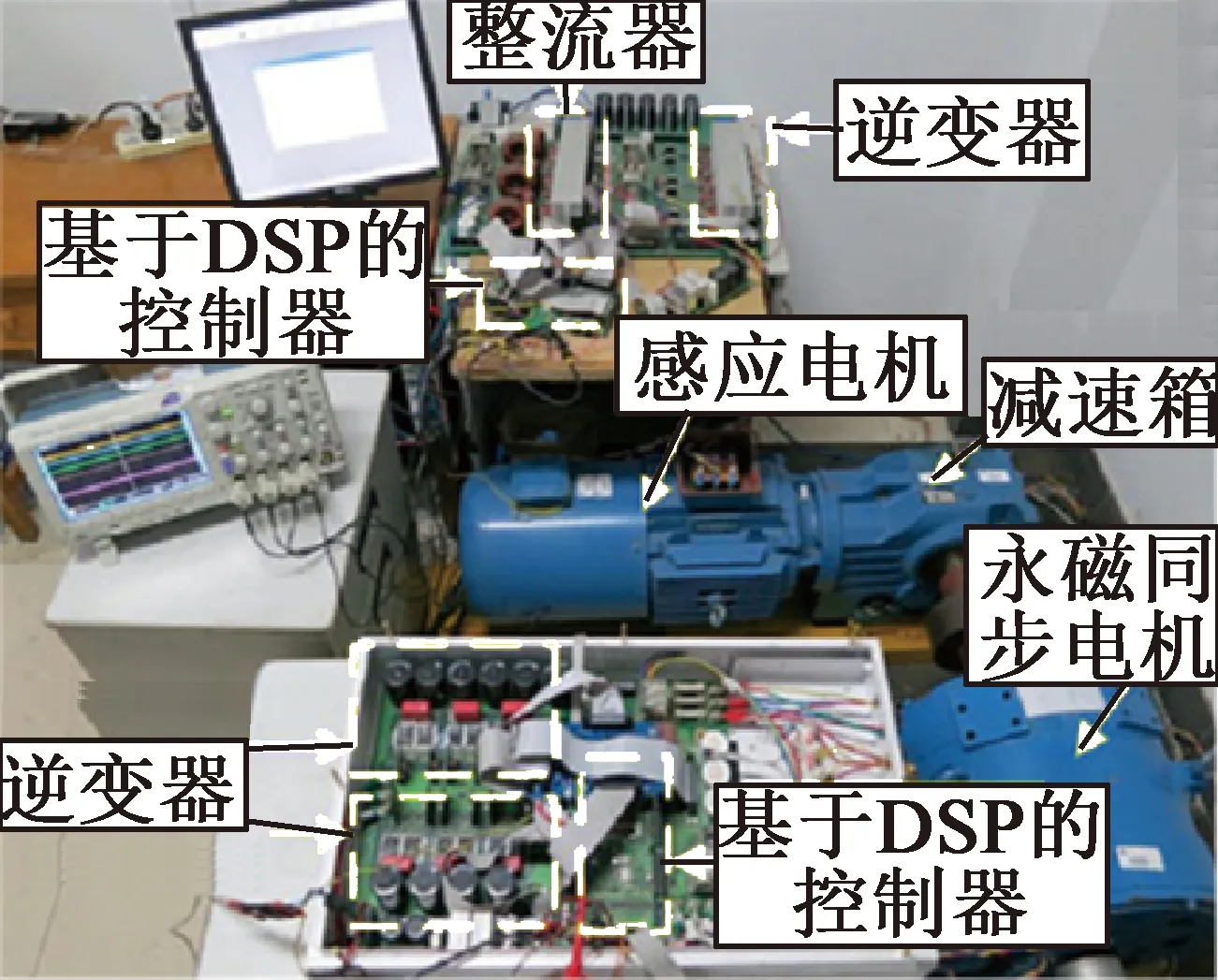
图7 IM传动控制系统试验平台

表1 试验平台中IM和永磁同步电机参数

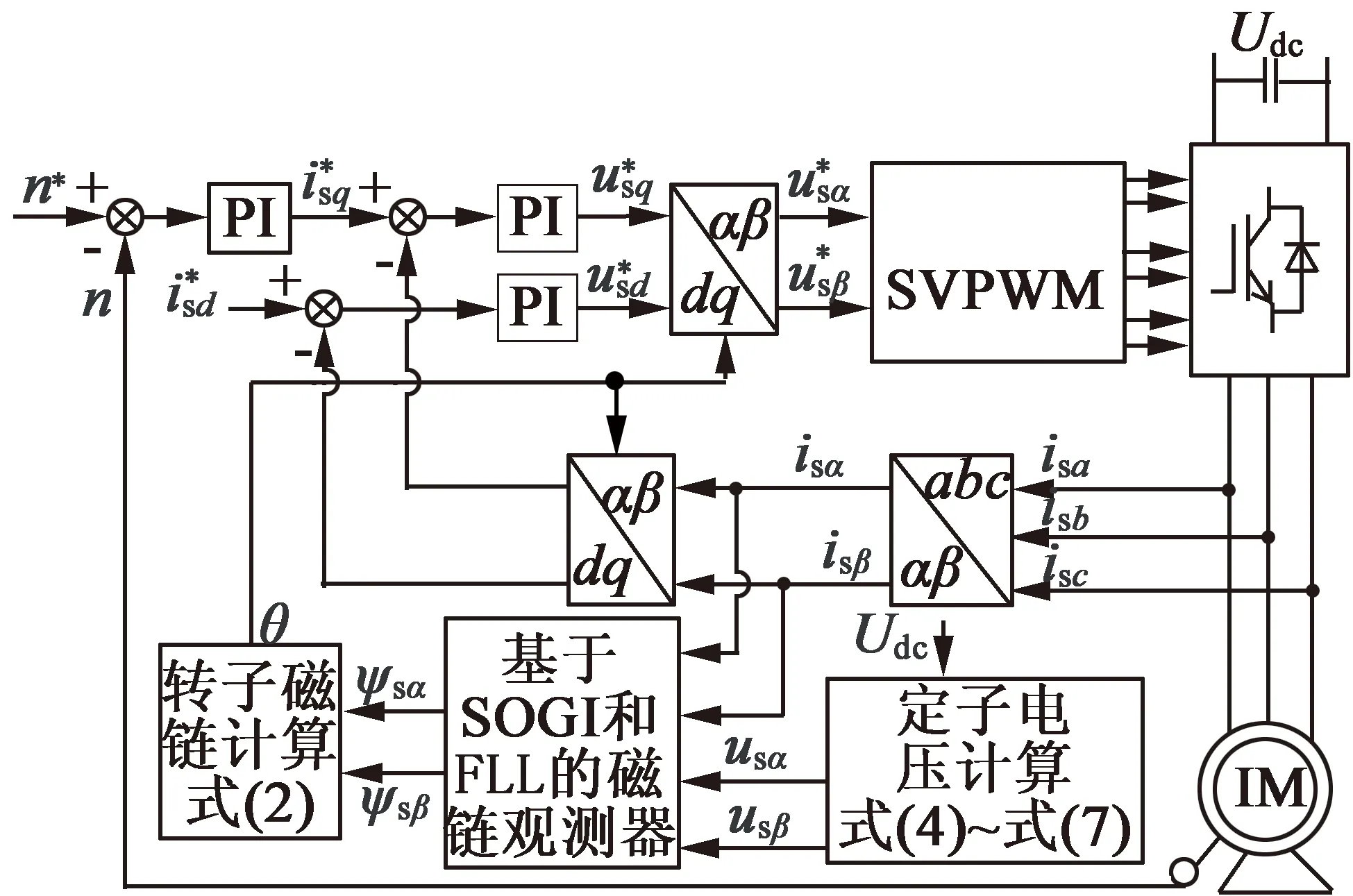
图8 IM驱动控制器设计框图

图9为稳态运行下分别采用纯积分器、低通滤波器和基于多级SOGI和FLL的磁链估计方案时的磁链估计立体图。从图9(a)中可以看出，转速在1 200 r/min时，采用纯积分器方案，磁链轨迹是垂直偏心的，这是由直流偏置造成的;而从图9(b)和图9(c)中可以看出，低通滤波器和基于多级SOGI和FLL的磁链估计方案解决了磁链轨迹偏心问题;同时可以看出，基于多级SOGI和FLL的磁链估计方案噪声较小，因为其高频衰减得到了显著改善。

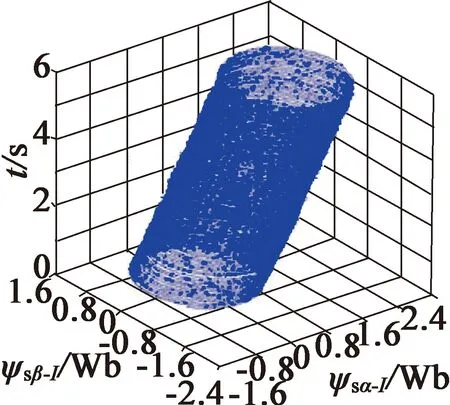
(a) 纯积分器方案

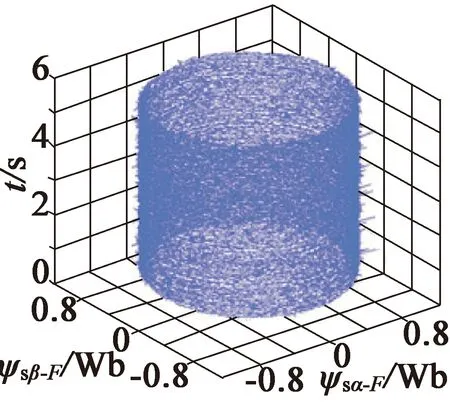
(b) 低通滤波器方案

(c) 基于多级SOGI和FLL的磁链估计方案

图10和图11分别为采用基于单级SOGI和FLL磁链估计方案和基于多级SOGI和FLL磁链估计方案时的估计转速ω′,α轴磁链ψsα_S和β轴反电动势esβ波形，此时IM转速为低速。图12和图13分别为采用基于单级SOGI和FLL磁链估计方案和基于多级SOGI和FLL磁链估计方案时的估计转速ω′,α轴磁链ψsα_S和β轴反电动势esβ波形，此时IM转速为高速。在这些波形图中，esβ和ψsα_S同相，因为这2个变量的相对位置滞后90°和α-β轴的滞后匹配抵消。对比图10和图11可以看出，在低速工况下，采用传统基于单级SOGI和FLL的磁链估计方案计算的esβ严重失真，进而导致估计的磁链ψsα_S波形失真；而在采用基于多级SOGI和FLL的磁链估计方案后，esβ波形更为平滑，从而估计的磁链ψsβ_S波形更为准确，而对比图12和图13可以看出，在高速工况下，2种方案的磁链估计效果相当，均较为准确。

(a) 估计转速

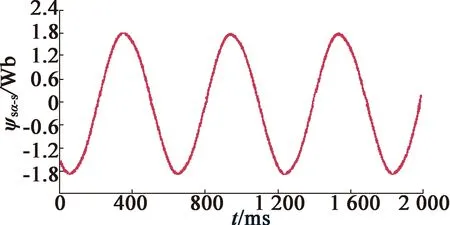
(b) α轴磁链

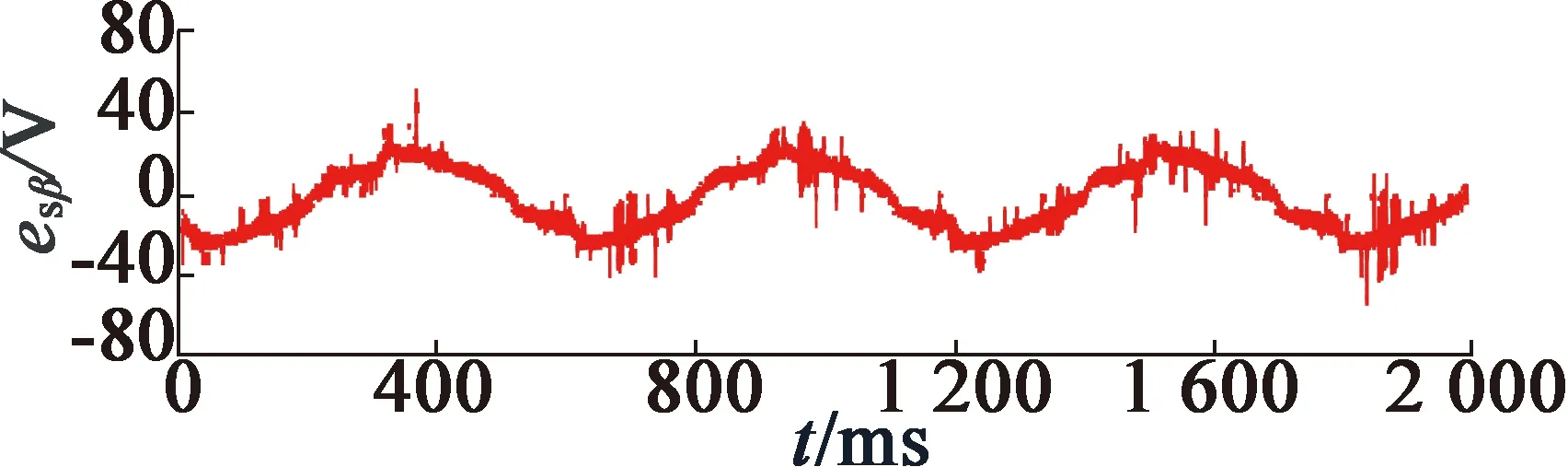
(c) β轴反电动势

(a) 估计转速

(b) α轴磁链

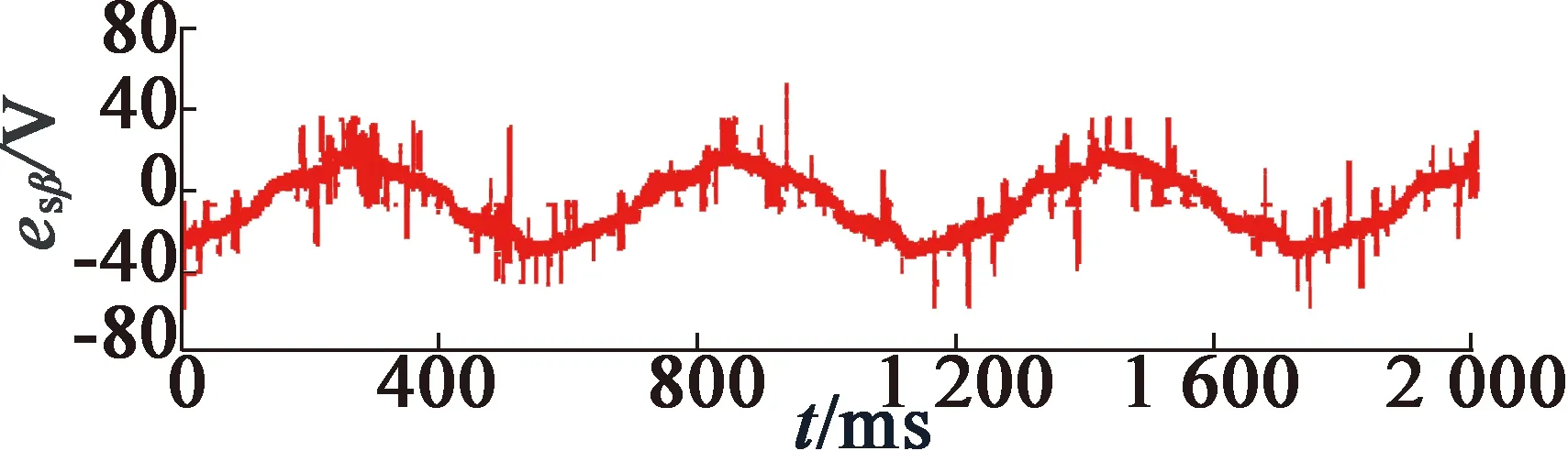
(c) β轴反电动势

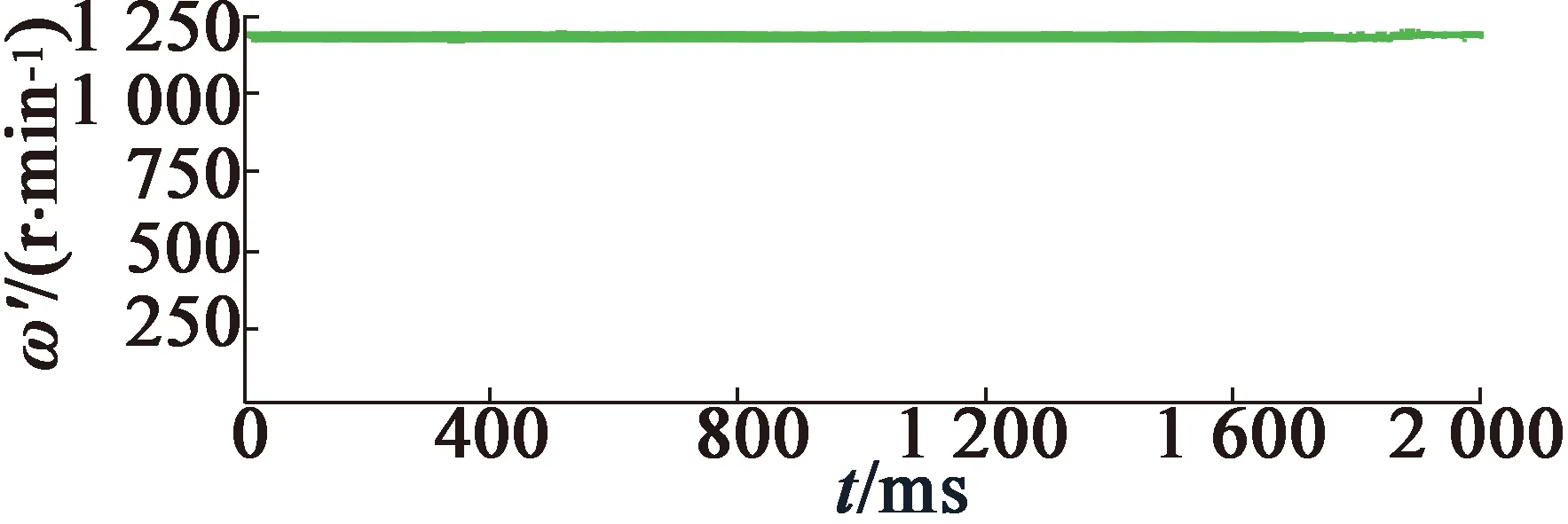
(a) 估计转速

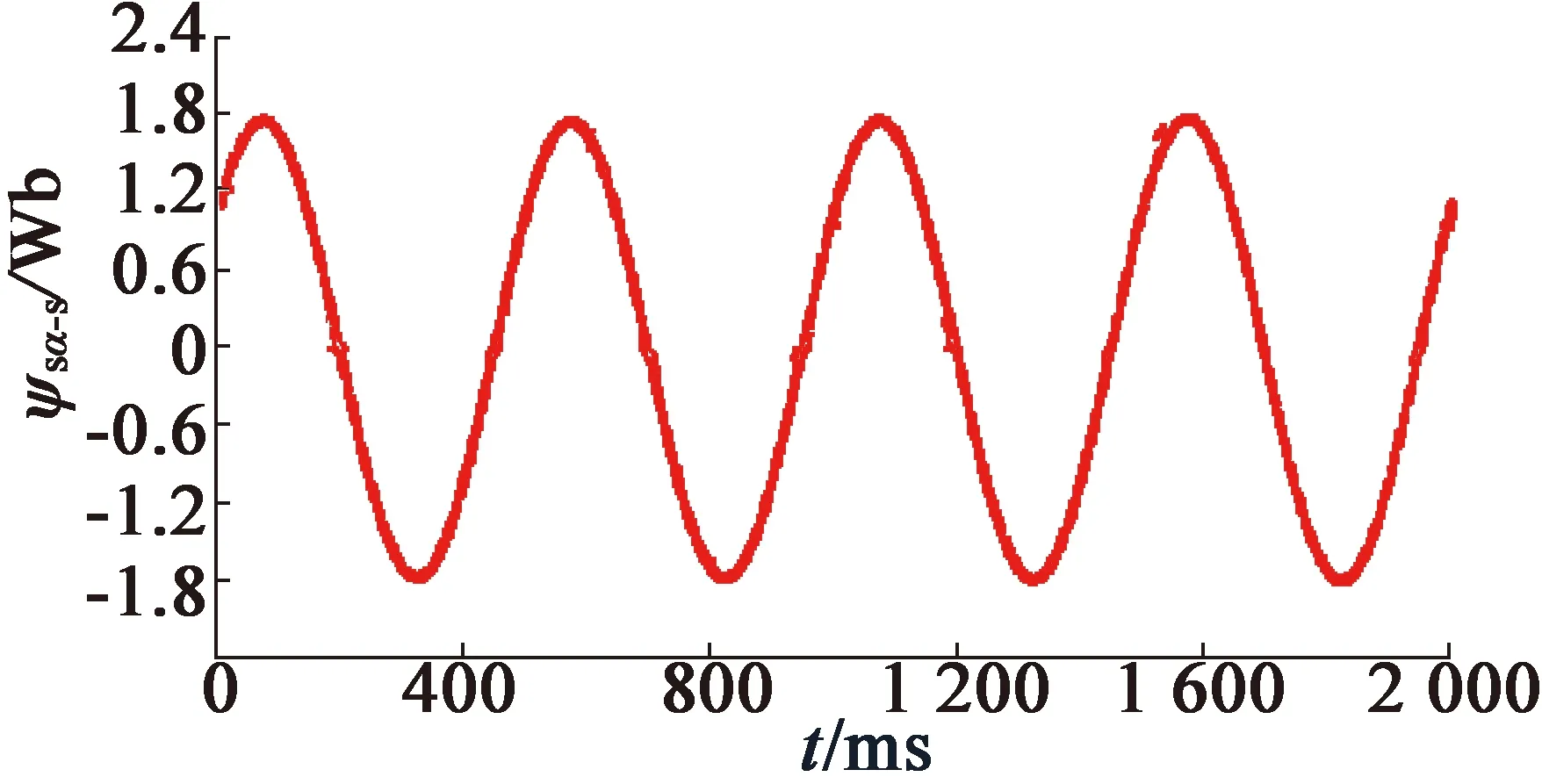
(b) α轴磁链

(c) β轴反电动势

(a) 估计转速

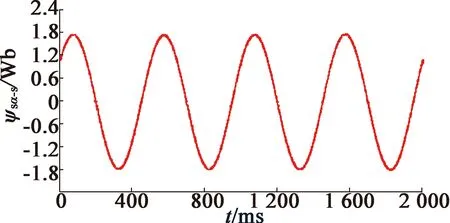
(b) α轴磁链

(c) β轴反电动势

图14为IM转速变化过程中，即转速从500 r/min变化到1 200 r/min时，采用新型多级SOGI和FLL的磁链估计方案时的β轴反电动势esβ、估计转速ω′,α轴磁链ψsα_S和转速ω的波形。从图14中可以看出，计算得到的ω′随转速成比例地正确变化，而且估计磁链的变化也较快地跟踪到新的稳态，验证了新方案的动态性能较好。

(a) 转速

(b) 估计转速

(c) α轴磁链

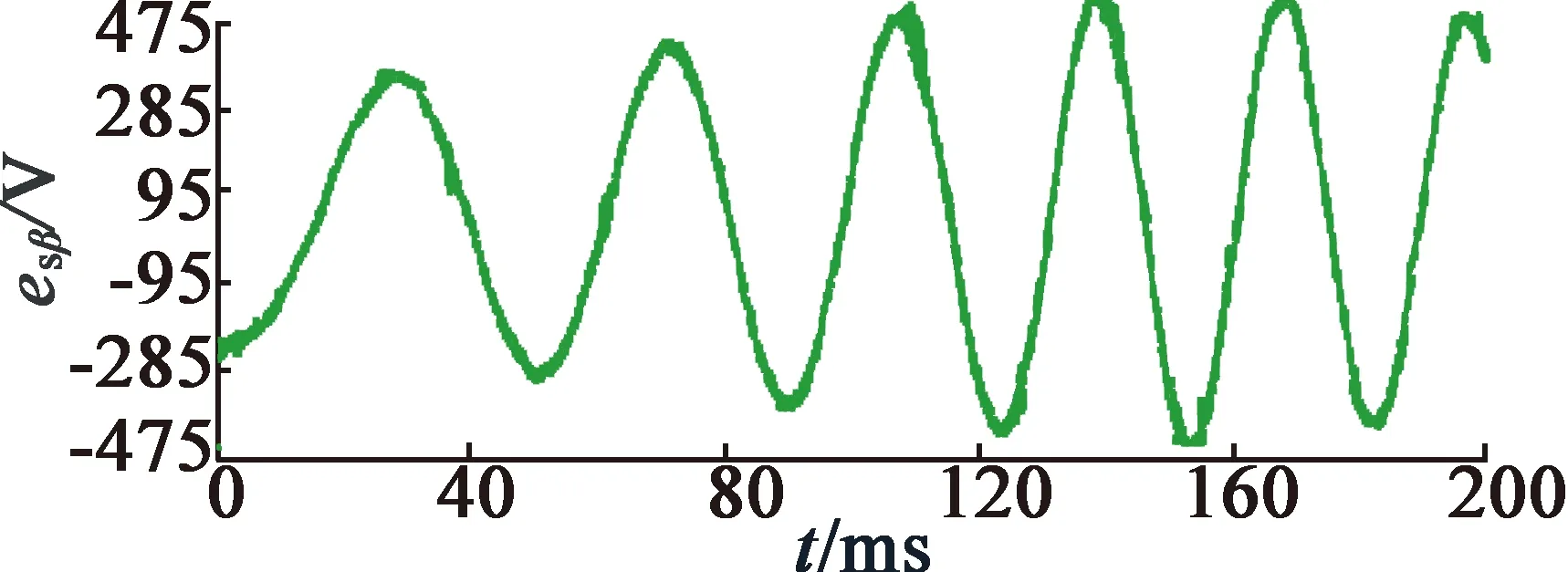
(d) β轴反电动势

4 结 语

围绕着IM驱动系统高性能控制器中磁链估计问题，设计了一种新型的基于多级SOGI和FLL的磁链估计器。采用传统方案逐渐升级递推的设计思路，完成了新型磁链估计器的设计，并开展了实验研究，现总结如下：

1) 新型的基于多级SOGI和FLL的磁链估计器较之传统纯积分磁链估计器方案、低通滤波器磁链估计器方案和基于单级SOGI和FLL的磁链估计器方案，避免了不同初始条件或直流偏置导致的饱和问题，同时不需要对基波幅值和相位进行补偿，而且高频性能得到了显著优化。

2) 稳态结果表明，采用基于多级SOGI和FLL的磁链估计器方案后的控制器磁链估计计算准确，同时动态实验结果验证了磁链估计动态跟踪性能也较好。

[1] 吴文进，苏建徽，刘鹏，等．感应电机全阶磁链观测器设计及其控制性能对比分析[J]．电机与控制学报，2016，20(4)：78-83．

[2] 蒋林，吴俊，杨欣荣．感应电机模糊自适应全阶磁链观测器的仿真研究[J]．电气传动，2016，46(8)：31-35．

[3] 史宏宇, 冯勇．感应电机高阶终端滑模磁链观测器的研究[J]．自动化学报，2012，38(2)：288-294．

[4] 梅柏杉，高宁，刘东洋．基于闭环直流偏置补偿积分器的新型定子磁链观测器[J]．电机与控制应用，2016，43(6)：28-33．

[5] CHO K R,SEOK J K.Pure-integration-based flux acquisition with drift and residual error compensation at a low stator frequency[J].IEEE Transactions on Industry Applications,2009,45(4):1276-1285.

[6] WANG G,DING L,LI Z,et al.Enhanced position observer using second-order generalized integrator for sensorless interior permanent magnet synchronous motor drives[J].IEEE Transactions on Energy Conversion,2014,29(2):486-495.

[7] 杨淑英，徐静，郭磊磊，等．基于二阶滑模的MRAS型感应电机转速辨识[J]．电力电子技术，2016，50(3)：94-97．

[8] 马文华，刘欣彤，刘海波，等．基于滑模观测器的电动汽车用感应电机驱动控制[J]．微特电机，2017，45(7)：68-73．

[9] COMANESCU M,XU L.An improved flux observer based on PLL frequency estimator for sensorless vector control of induction motors[J].IEEE Transactions on Industrial Electronics,2006,53(1):50-56.

[10] 韦文祥，刘国荣．基于扩展状态观测器模型与定子电阻自适应的磁链观测器及其无速度传感器应用[J]．中国电机工程学报，2015，35(23)：6194-6202．

[11] WANG Y,DENG Z.Improved stator flux estimation method for direct torque linear control of parallel hybrid excitation switched-flux generator[J].IEEE Transactions on Energy Conversion,2012,27(3):747-756.

[12] 潘月斗，陈虎．基于高增益观测技术的高精度感应电机磁链观测器研究[J]．控制与决策，2014，29(8)：1495-1500．

[13] WANG Y,DENG Z.An integration algorithm for stator flux estimation of a direct-torque-controlled electrical excitation flux-switching generator[J].IEEE Transactions on Energy Conversion,2012,27(2):411-420.

[14] 邓哲，周峰武，林辉品，等．电网故障时基于双输入SOGI-FLL的新型电网快速同步方法[J].电工技术学报，2013，28(12)：32-43．

[15] RODRIGUEZ P,LUNA A,CANDELA I,et al.Multiresonant frequency-locked loop for grid synchronization of power converters under distorted grid conditions[J].IEEE Transactions on Industrial Electronics,2010,58(1):127-138.