基于蚁群-粒子群的模糊神经网络超声波电动机控制

乔维德，张本法

(1.无锡开放大学，无锡 214011；2.常州开放大学,常州 213001)

0 引 言

超声波电动机(以下简称USM)是20世纪末发展起来的一种微小型驱动电机。与传统的电磁电机相比，USM结构紧凑、体积小、质量小，微位移、低转速、大转矩，运行无噪声，不受电磁干扰，耐低温这些特性，是一种较为理想的伺服驱动执行器件，已广泛应用于航空航天、医疗器械、精密微动机构、办公自动化、机器人工业、高档汽车、军事及工业控制等领域。因USM自身参数的高度非线性、时变性，特别是电机工作中伴随严重的摩擦过程，运行特性呈现很多非线性和不确定因素，而且USM受温度和外加负载的影响较大，所以难以建立精确的数学模型，很难通过传统控制方法实现高精度的速度伺服控制[1]。目前很多学者和科技人员为解决USM的驱动问题，做了许多探索和试验，如应用PID控制、模糊控制、神经网络等来优化控制USM，然而采用以上方法时，仍然不能有效解决USM转速波动较大及运行不稳定的问题，从而不能保证USM精确的转速跟踪和优良的动态控制性能。综上所述，本文研究将蚁群算法和粒子群算法组成递阶结构优化模糊神经网络的USM转速控制方法，即应用蚁群算法的全局搜索和粒子群算法的局部搜索功能，优化模糊神经网络控制器的结构参数，并且将该控制器引入USM的转速控制系统。仿真分析及试验结果验证了本控制系统具有较强的转速跟踪与响应能力，并且控制精度高，抗干扰能力强。

1 USM转速控制系统

图1是USM转速控制系统原理示意图。由速度参考模型设定电机的转速跟踪目标，可以是恒定转速、阶跃转速等。在系统转速控制内环中引入电机定子的振动信号检测单元，以增强USM的速度跟踪准确度，提高USM的速度响应快速性。控制原理结构中的模糊神经网络(以下简称FNN)控制器的功能是控制USM的转速，其输入量分别为转速误差e和误差e的变化率Δe，e由系统结构中参考模型的给定转速信号n*与USM转速检测部件实际转速量n比较计算得出，即e=n*-n。模糊神经网络控制器结构参数通过蚁群算法在线优化求取，以保证USM控制系统的实际输出转速n能及时准确跟踪参考模型的给定转速输出n*，即e→0。

图1 超声波电动机转速控制原理图

2 FNN控制器

USM参考模型自适应转速控制系统中FNN控制器结构如图2所示。控制器由输入层(i层)、隶属函数层(j层)、规则层(k层)、输出层(o层)共4层前向神经网络组成[2]。

图2 FNN控制器结构模型

在FNN输入层中，转速误差e及其变化率Δe由输入层i节点传至第2层，可以表示：

(1)

(2)

FNN的隶属函数层(模糊化层)主要负责对输入变量模糊化，每个变量各自以模糊子集{N3(负大)、N2(负中)、N1(负小)、Z0(零)、P1(正小)、P2(正中)、P3(正大)}来表征。模糊子集中的隶属度函数为该层的输出量，采用高斯基函数形式表示隶属度函数。该层第j个节点的输出与输入可表示：

(3)

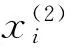
在FNN的规则层中，每个节点对应相应的模糊逻辑运算规则。即：

(4)

FNN的最后一层是输出层，它只有1个节点，其输出量为规则层输出信号经处理后的总和。

(5)

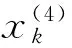
3 FNN控制器结构参数的优化

对上述FNN控制器的结构参数优化过程，就是通过学习训练不断调整和更新高斯隶属度函数参数mij和δij,连接权值ωjk和ωko过程，所以可调参数mij,δij,ωjk,ωko对模糊神经网络控制器性能产生重要影响。由于本控制系统中e及其变化率Δe2个输入变量共有14个模糊子集，因此需要训练的mij和δij各14个；规则层神经元个数为Nj=7×7=49，故模糊神经网络需要训练的参数共49+2×14+49=126个。以往采取传统的BP梯度下降法,优化FNN的结构参数，收敛速度慢，比较容易陷入局部极小值，而且优化效率较低。为此本文提出将全局搜索的蚁群算法作为主级，将局部搜索的粒子群算法作为从级，组成主从递阶结构对FNN参数进行训练优化，可以提高FNN的泛化能力和快速全局收敛等。

3.1 蚁群算法

蚁群优化(以下简称ACO)算法属于一种随机搜索的智能优化算法，它是以模仿蚂蚁群体间的传递信息行为来实现类似搜索食物源的寻优算法。蚂蚁在行走路程中，一般会留下一种特殊的化学物质——信息素，所有蚂蚁都是根据此信息素以及信息素浓度而决定自身的行走路线，并始终向着高浓度信息素的路径方向运动。越多的蚂蚁通过某条路径，后面的蚂蚁选取这条路径的机率就越大。蚂蚁个体间正是以此信息交流方式来选择最优路径，并实现最快捷搜索食物源的目的。设待学习优化的模糊神经网络有m个参数，包括所有的网络权值和阈值(如mij,δij,ωjk,ωko共126个，即m为126)，设定P1,P2,…,Pm，将Pi(1≤i≤m)设定成N个非零随机数，并形成集合IPi。假设蚂蚁的数量是S，所有蚂蚁均由集合IPi出发搜索食物，按照集合IPi每个元素的信息素状态，从集合IPi随机选择唯一元素，并且对其信息素进行及时更新[3]。第K(K=1,2,…,S)只蚂蚁依此在每个集合IPi中选择第j个元素，直至蚂蚁全部到达食物源。路径选择概率规律为：

(6)

通过式(7)和式(8)更新集合IPi元素的信息素：

τj(IPi)(t+1)=ρτj(IPi)(t)+Δτj(IPi)

(7)

(8)

(9)

式中：Q是用来控制信息素的调节速度，一般设为常数；eK是蚁群中第K只蚂蚁在本次循环所经历的路径总长度。为克服ACO算法早熟和局部收敛问题，这里采取自适应更新信息素方法。将信息素量值限制在[τmin，τmax],将式(7)变换如下：

τj(IPi)(t+1)=

ρ1+φ(m)τj(IPi)(t)+Δτj(IPi)τ>τmax

(10)

τj(IPi)(t+1)=

ρ1-φ(m)τj(IPi)(t)+Δτj(IPi)τ<τmin

(11)

式中:φ(m)表示与迭代次数成正比的函数。

3.2 粒子群算法

粒子群优化(以下简称PSO)算法将需要优化和解决的问题当成某一搜索空间d范围内的鸟，简称“粒子”，粒子所处位置即为待求的潜在解。标准PSO算法根据式(12)和式(13)进行迭代，直至搜寻粒子群中达到最小误差要求的最优位置[4]。

Vij(t+1)=ωVij(t)+C1R1[Pj(t)-Xij(t)]+

C2R2[Gj(t)-Xij(t)]

(12)

(13)

式(12)、式(13)中，j=1,2,…,d；t为迭代次数；Xij(t),Vij(t)分别为第t代粒子位置和速度；C1,C2表示学习因子；R1,R2取值范围为[0，1]。为克服PSO算法的早熟与振荡现象，让惯性权重ω根据粒子适配值作自动调节，即：

(14)

式中：f，fave，fmax分别代表粒子的适应度值、平均适应度值以及最大适应度值。

3.3 蚁群-粒子群算法优化网络参数过程

ACO比较容易产生停滞现象，搜索时间较长。PSO又具有较快的寻优求解速度，因此将ACO和PSO组成ACO-PSO混合算法，以优化模糊神经网络参数。ACO将网络需要训练的参数在取值范围内求得有限个离散值[5]。PSO搜索寻优实际上是粒子速度和位置的改变过程，所以FNN学习算法中的高斯隶属函数均值、标准差和权重应该与粒子的位置相对应。

第1步 初始化。蚁群初始化主要设定时间、迭代次数NC、最大迭代次数NCmax、蚂蚁数目S、初始信息素ρ等，且让全部蚂蚁放置在蚁巢；粒子群初始化包括设置粒子数h、粒子初始位置、速度、惯性因子ωmax和ωmin、加速因子C1和C2、最大迭代次数Mp等。

第2步 起动全部蚂蚁，第K(K=1,2,…,S)只蚂蚁从集合IPi开始，按次序从IPi中选取元素，直至蚁群中所有蚂蚁均搜寻到食物源。

第3步 将每只蚂蚁选取值作为FNN结构参数训练样本，然后按照式(15)求取其网络输出平均相对误差，记录目前FNN结构参数最好解[5],且根据式(8)～式(11)对全部集合中各元素信息素更新调整。式(9)中eK定义为FNN期望输出与实际值的平均相对误差。定义公式：

(15)

式中：yi表示FNN的实际输出值;Oi代表FNN期望输出值;S为蚂蚁样本数量。因此，当网络训练输出误差eK减小时，相应信息素浓度就增大。式(10)和式(11)中的φ(m)=m/15，其中m为连续收敛次数。

第4步 采用PSO改进第3步中求得的最优解。首先按式(15)计算粒子适应度，并按式(12)和式(13)及时更新粒子的运行速度与所处位置。假如当前找到的粒子最好位置Pbest不能优于粒子当前位置Pnow，那么令Pbest=Pnow；假如当前搜出的全局最好位置Gbest不能优于粒子当前位置Pnow，那么令Gbest=Pnow。如果没有达到粒子群最大迭代次数，继续对粒子当前位置与最优位置Pbest及Gbest进行比较执行。

第5步 循环次数增1。若目前最优解得到改进，更新信息素浓度[5]。

第6步 如果进化满足最大迭代次数，便停止迭代过程，同时得出最优解，否则将跳至第2步循环执行。

4 仿真分析

利用MATLAB/Simulink对USM控制系统进行仿真研究。应用ACO与PSO结合(即ACO-PSO混合算法)训练优化模糊神经网络。各参数选取：ρ=0.7，Q=20，NCmax=300，S=100；h=30，Mp=55，ωmax=1.6,ωmin=0.3,C1=C2=2。为对比不同算法训练模糊神经网络性能优劣，本文采用同样的训练样本，先后通过ACO、PSO及ACO-PSO 3种算法对FNN加以学习，训练结果如表1所示。由表1分析得到，采用ACO-PSO混合算法训练FNN，训练时间较短，训练精度较高，无论是在寻优时间效率上还是寻优精度方面，都取得较好的优化性能。

表1 三种算法的模糊神经网络训练结果

图3、图4分别是设定目标转速90 r/min且带0.2 N·m负载时，本文设计的经ACO-PSO优化FNN方法和按BP算法优化的传统FNN方法USM系统速度仿真特性曲线。在稳态时图4的速度波动较图3大且明显。与传统的BP算法优化FNN控制相比，经ACO-PSO优化FNN控制器的控制系统的动态响应与静态特性明显优于传统FNN控制。

图3 ACO-PSO优化FNN

图4 传统BP训练FNN

为验证经ACO-PSO算法优化的FNN控制器的抗干扰能力，t=0.15 s时刻又突加0.4 N·m负载，并同传统BP算法训练的FNN控制进行比较分析。从图5、图6对比可知，当系统突加负载时，由ACO-PSO算法优化的FNN系统能使USM速度迅速稳定在90 r/min，转速响应快，转速波动小，对外界负载扰动能快速自动调节，抗干扰能力强，稳态后系统控制精度较高，而传统BP算法训练的FNN，当突加2倍负载时，出现较大的转速超调及脉动。所以，综合USM起动、速度跟踪及负载扰动情况而言，经ACO-PSO算法优化的FNN控制器具有更好的动态特性和鲁棒性。

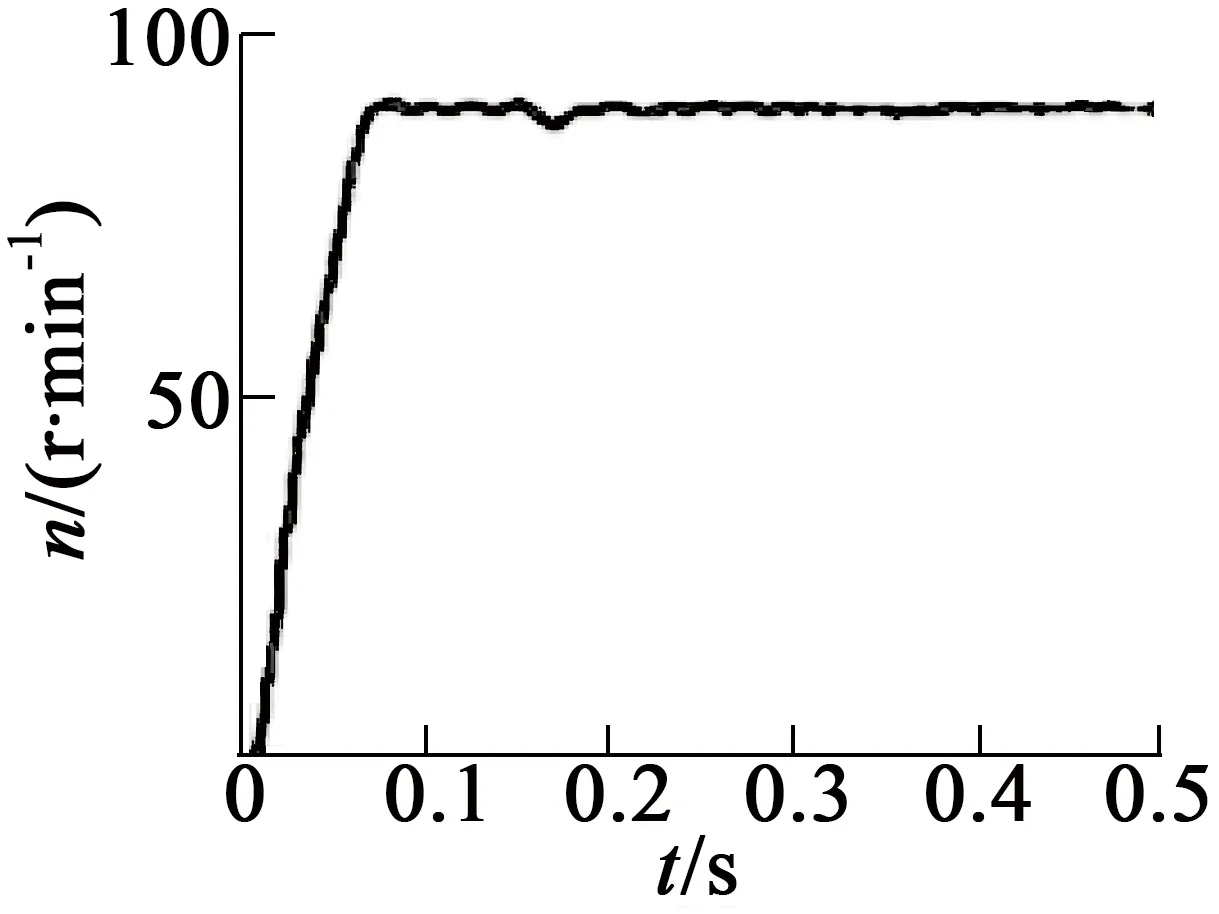
图5 ACO-PSO优化FNN突加负载时速度响应

图6 传统BP训练FNN突加负载时速度响应

5 实验验证

基于DSP的USM转速控制系统结构原理框图及实验平台如图7、图8所示[6]。

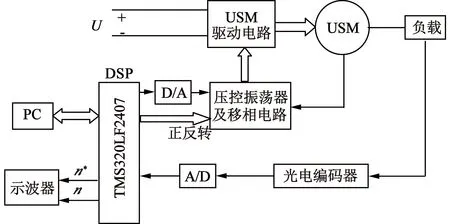
图7 USM速度控制结构原理图

图8 USM速度控制实验平台截图

控制系统由PC机、DSP(数字信号处理器)、USM驱动器、光电编码器、示波器等功能设备组成。USM为直径60 mm行波型电机，DSP选用TMS320LF2407芯片。光电编码器选用5 000线Model775A。现场实验测试时，通过光电编码器将USM的旋转角位移转换成连续的电脉冲信号，再通过F/V(频率/电压)变换和A/D(数/模)转换后传给DSP，DSP处理后转换为速度值，作为输入变量供给DSP进行实时计算，同时通过DSP的串行口传送至PC机进行显示和保存。数据采样频率选取为1 000 Hz。通过USM速度参考输入量及实际转速反馈量的比较运算，在压控振荡器(采用CD4046)的控制端输出控制电压，从而改变USM驱动电路频率，有效驱动USM。

利用示波器观察设计的控制系统，分别跟踪恒定目标转速80r/min和阶跃目标转速80r/min→50 r/min→80 r/min→50 r/min时的实验结果，如图9、图10所示(USM负载力矩为0.5 N·m)。

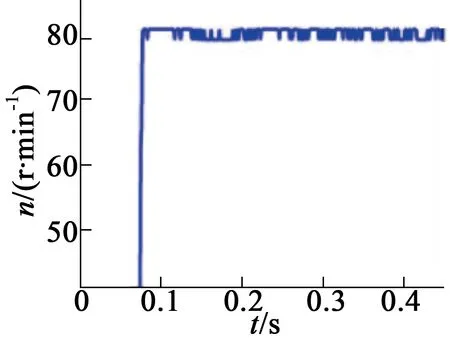
图9 USM恒转速跟踪曲线

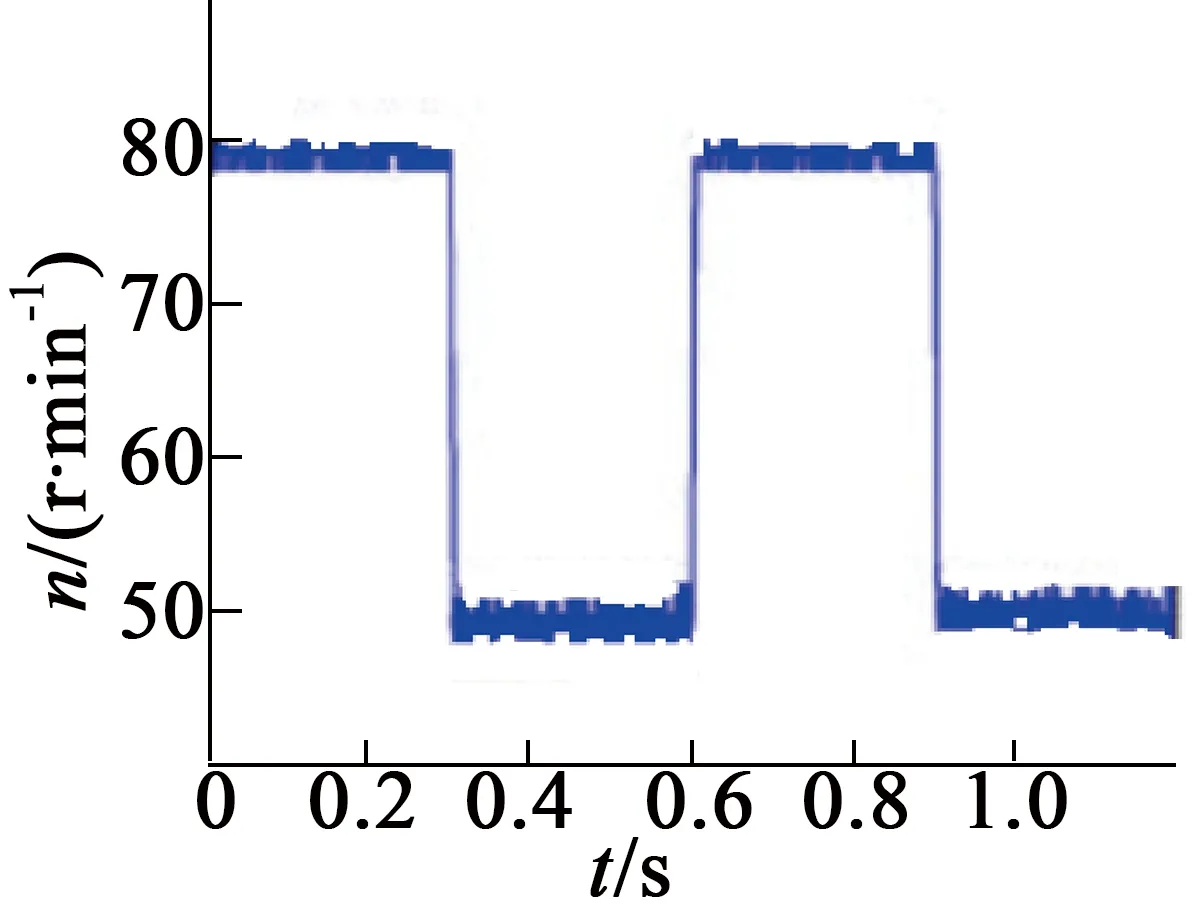
图10 USM阶跃转速跟踪曲线

图9中USM跟随目标转速的波动很小，仅在±1.8 r/mim左右，近似一条直线，说明对负载的适应性较强。图10中当USM目标转速设为80 r/min时，实测的转速波动范围为±1.7 r/mim；当目标转速阶跃为50 r/min时，实测运行的转速波动范围为±2.1 r/mim。

5 结 语

本文用ACO和PSO相结合形成的ACO-PSO混合算法，优化FNN控制器的高斯隶属函数参数和神经网络权值，并应用于USM的自适应速度跟踪系统，电机转速跟踪性能强，转速脉动明显减小，控制精度也得到明显改善。该系统呈现出较强的适应性和鲁棒性，取得较为满意的优化控制成效，为USM智能化控制提供一种新的技术方案，有一定的工程参考与应用价值。

[1] 黄帆,金龙,徐志科,等.基于卡尔曼滤波的超声波电动机测速算法研究[J].微特电机,2015,43(11):1-4.

[2] 乔维德.遗传算法优化的开关磁阻电动机RFNN位置控制器设计[J].微特电机,2016,44(2):75-77.

[3] 乔维德.基于蚁群模糊神经网络的无刷直流电机仿真控制研究[J].电气传动自动化,2009,31(5):6-10.

[4] 乔维德.改进粒子群优化神经网络的变压器故障诊断[J].电工电气,2015(12):24-27.

[5] 于万霞,杜太行,郑宏兴.基于蚁群粒子群的模糊神经网络交通流量预测[J].计算机工程与应用,2007,43(25):197-199.

[6] 乔维德.一种改进的提升机同步电机直接转矩控制[J].盐城工学院学报,2017,30(1):28-33.