过盈联接磁悬浮转子的模型修正方法分析

施梦瑶，魏朝富，谢思源，李 朋

(武汉理工大学，武汉 430070)

0 引 言

在超高速旋转机械中，磁悬浮技术凭借无摩擦、可控制的独特优势成为研究热点。目前高速磁悬浮电机等柔性转子实现高转速的瓶颈在于如何安全穿越弯曲临界转速[1]。对过盈联接转子系统模态的准确分析，旨在精确模型参数，便于之后的控制研究。

有限元法基于物理模型，如何处理过盈配合部位,对于准确构建模型是一个难题。例如高速电机中护套作为主要抗弯载体，主要考虑其刚度和惯量，文献[2]在配合部位将转子组件的分布质量向轴的两端集中；磁力支承转子系统中转子组件皆热过盈配合在转子心轴上，文献[3]通过减小附加部件的弹性模量来模拟过盈问题；过盈配合实际上是一个局部的接触问题，当因配合而产生的局部应力对于整体模态的计算不可忽略时，需要在模型建立的过程中将过盈量纳入考虑。接触问题具有高度非线性行为，在进行迭代求解的过程中，过大的刚度总是会引起严重的收敛困难[4]。文献[5]将过盈量转为接触刚度的优化问题；增广拉格朗日法引入额外因子降低了对于惩罚刚度的敏感性, 文献[6]采用摩擦接触类型，将局部应力结果导入之后的模态分析，得到了更为精确的模态计算结果。

针对柔性磁悬浮转子，以一阶及二阶弯曲固有频率为主要预测对象，研究过盈配合引起的固有频率变化问题。最后通过模态测试，依据实验数据对不同模型修正方法进行分析。

1 接触力问题基础理论

1.1 过盈配合下的接触压力

简单的过盈装配如图1所示。设轴及衬套为相同材料，E为弹性模量；μ为泊松比；δ1，δ2分别为轴和衬套的径向位移量；δ为配合的过盈量。

图1 轴与衬套过盈装配示意图

有边界条件[7]：

δ2|r=b-δ1|r=b=δ

(1)

依据弹性力学理论：

(2)

(3)

结合式(1)～式(3)，在r=b处的接触面压力可表示：

(4)

对于实心轴的配合，接触压力可表示：

(5)

1.2 过盈配合下的接触算法

1) 罚函数方程:

FNormal=kNormal·xP

(6)

式中：FNormal为接触力；kNormal为接触刚度；xP为穿透量。

针对一个有限接触力FNormal，存在一个接触刚度的概念kNormal。参考图2，弹簧只在接触面间有一定穿透量后才会发挥作用，且接触刚度与穿透量存在一个反比关系。

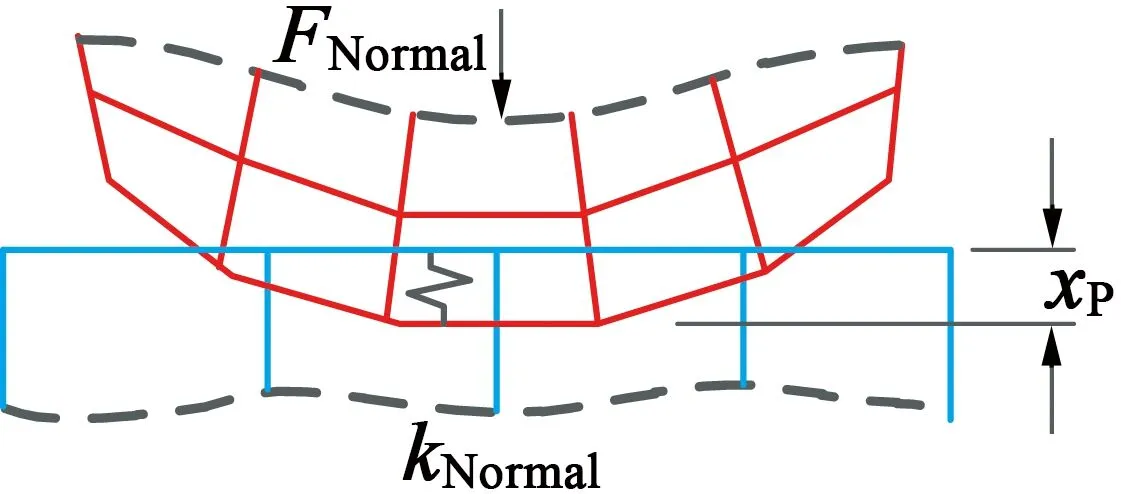
图2 接触刚度与穿透量示意图

接触刚度kNormal：ANSYS依据模型的几何特征、材料参数、用户定义的接触类型及接触刚度系数fFKN来计算接触刚度。根据节点计算的刚度要乘上fFKN，为增加求解精度可修改fFKN值。即：

2) 增广拉格朗日法:

FNormal=kNormal·xP+λ

(7)

因为额外因子λ的引入, 增广拉格朗日方法对于接触刚度kNormal变得不敏感。

2 柔性磁悬浮转子系统的有限元分析

2.1 柔性磁悬浮转子装配体结构

磁悬浮转子的柔性表现在其设定的工作转速常位于一阶甚至二阶临界转速之上，建立一个实验模型对于研究高速环境下磁悬浮转子的动力学特性以及磁力轴承的支撑控制特性具有重要意义。

转子平台如图3所示。包括3个配重盘用以降低转子系统的固有频率并调整转子穿越临界转速时的振形；支撑结构由2个径向磁轴承组成，电机通过弹性联轴器与轴联接；另设置一个扰动激励磁轴承；固定环、位移检测环等转子组件皆通过热装配固定在心轴上。材料基本属性如表1所示。

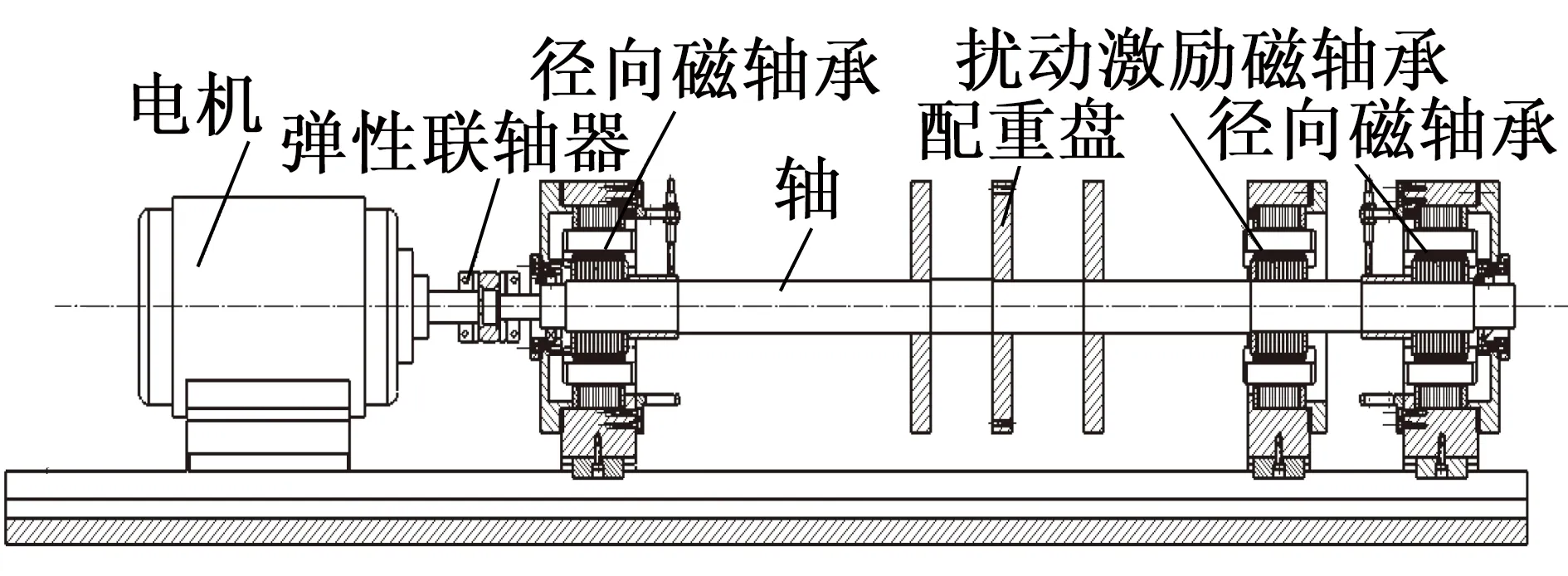
图3 柔性磁悬浮转子平台结构

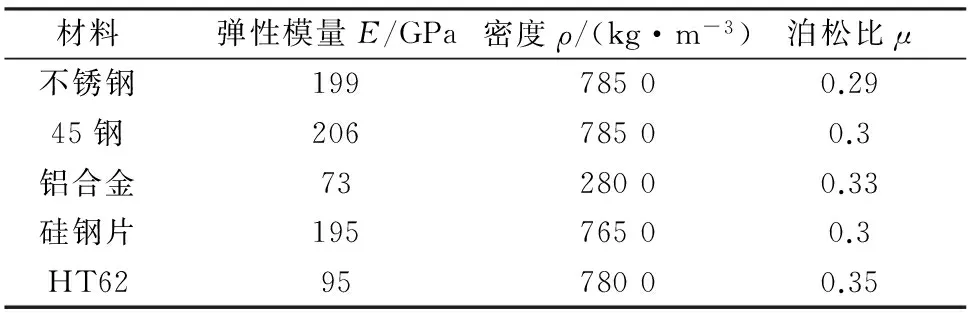
表1 转子装配体材料属性

2.2 等效参数下的有限元仿真分析

2.2.1 附加组件的等效

柔性磁悬浮转子体积小、质量轻，由过盈配合引起的刚度问题对于整体模态不可忽略。有限元求解中将复杂转子系统离散为有限尺寸梁单元，在不考虑耦合的情况下[8]，单元n的对称刚度矩阵Kn：

(8)

式(8)中:系统刚度矩阵的变量包含弹性模量E、转动惯量Jn、长度ln，长度的改变会同时引起质量矩阵的变化，不利于等效。实际的过盈配合中不存在质量的变化，修正参数过程中应遵循质量不变的原则。对于转子而言，惯性矩与直径相关，可以考虑通过改变弹性模量E及转子附加组件的直径d来改变系统刚度矩阵。据此，在建立模型前取一个修正系数α，与实际参数相乘，以等效参数的方式对计算模型进行修正。考虑到过盈配合装配体相对于一体化加工而言，其抗弯刚度必然是一个降低的趋势，因此修正系数α≤1。

在Workbench中进行装配体建模，以5 mm大小进行扫掠和映射相组合方式的网格划分，获得节点个数488 834，转子装配体物理模型及网格模型如图4所示。依次通过修正系数α来改变转子组件的弹性模量，记录下弯曲固有频率如表2所示。当修正系数取1时即为Workbench默认模型，计算结果误差达到7.4%。

(a) 物理模型

(b) 网格模型

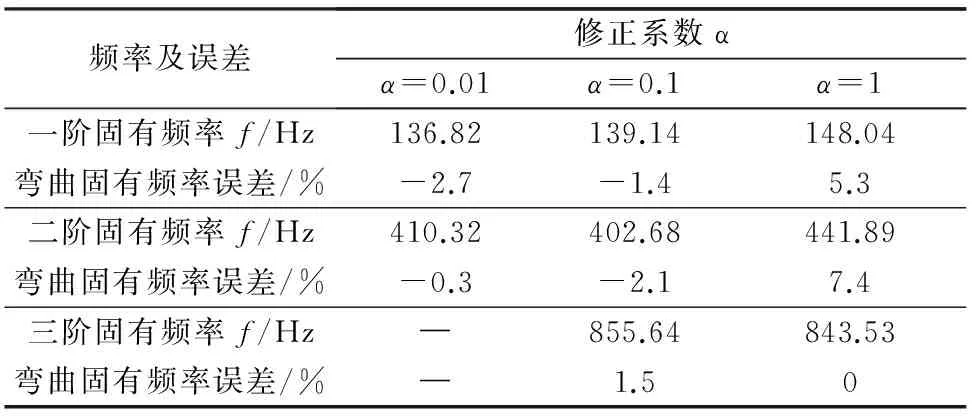
图4 转子装配体物理模型及网格模型对比

对于转动惯量的等效方式与上述步骤大致相同，依次通过修正系数α来改变转子组件的径向厚度。修正系数取0，即与转子心轴相配合组件的质量皆附加在相对应配合长度范围，将组件与心轴的质量相加，重新计算出密度并定义在新材料中。相同方式划分网格后模型节点数为145 453，相对于修正前网格节点数减少70%，便于计算。记录下的弯曲固有频率如表3所示。

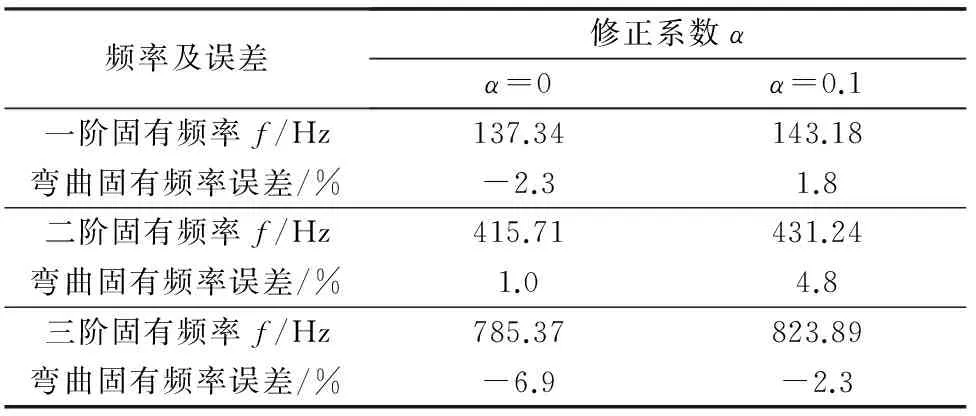
表3 外径修正系数下固有频率误差对比

在对弹性模量进行修正的过程中，系数取0.01时会引起系统刚度过小，出现很多本不该存在的轴向振动[3]，且难以出现三阶弯曲模态。系数取0.1时的计算结果较理想，相对误差不超过2.5%；通过外径对转动惯量进行修正，相对于修正弹性模量是一个复杂的过程。一般地,修正系数取为0，将转子组件全部附加到心轴上可获得一个较为保守的结果。

2.2.2 转子心轴的等效

转子心轴为一体加工材料，且转子组件分布较为均匀，对转子心轴进行等效建模可以简便计算。图5表达了随着心轴等效弹性模量的减小，转子系统前三阶固有频率呈现减小的趋势。

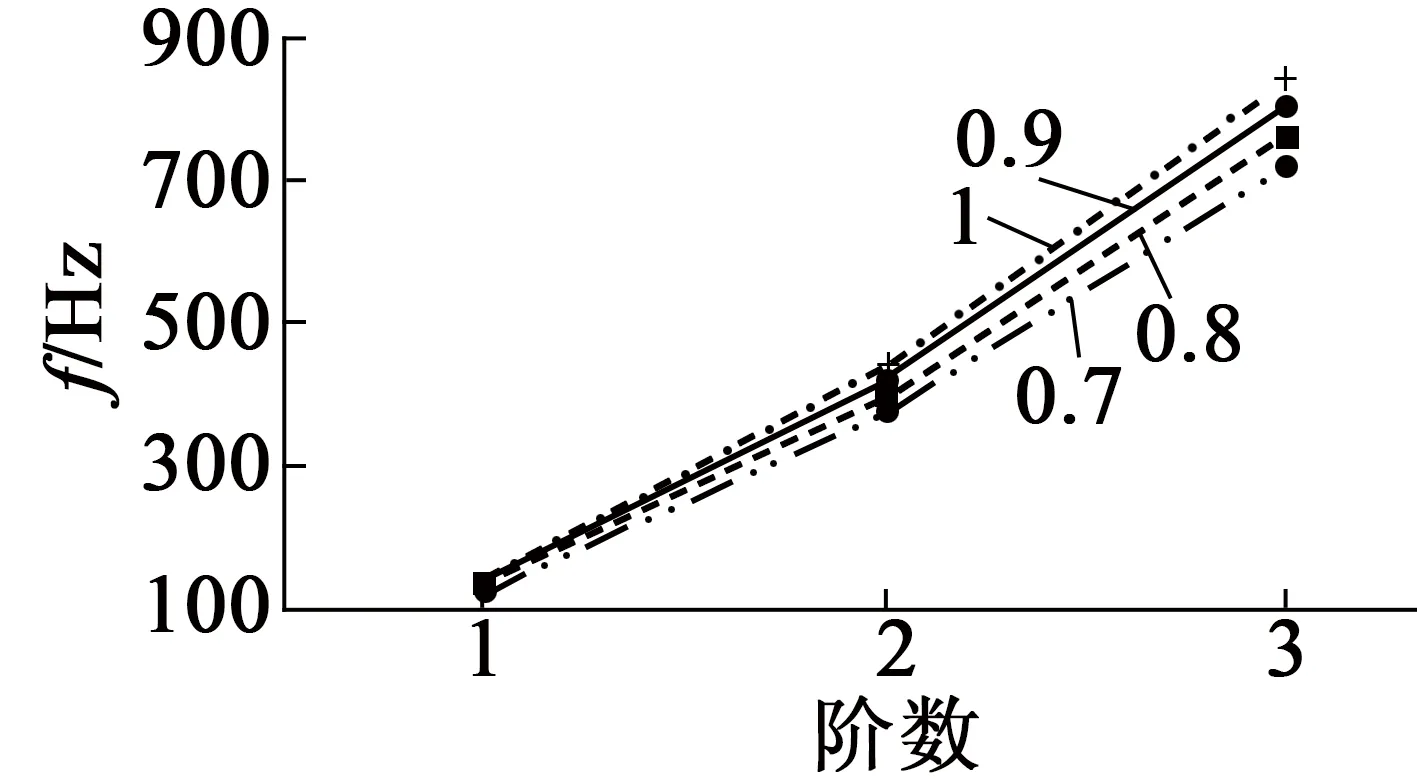
图5 弹性模量修正系数下固有频率变化趋势

对心轴进行修正，将得到的固有频率与测试值进行对比，记录于表4中。

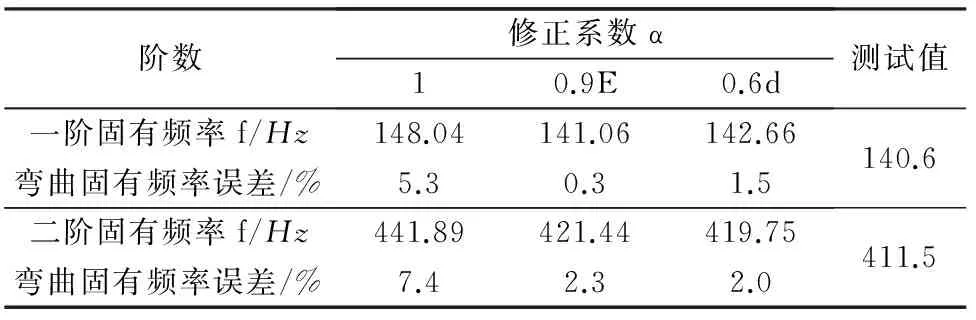
表4 心轴不同修正方式下固有频率与模态测试值对比

转子心轴作为主要的抗弯载体，其弹性模量修正系数应趋近于1。相比于转子组件中0.1的修正系数，心轴的弹性模量修正系数选取0.9更接近测试值。而对于心轴内径的修正，其主要问题在于针对阶梯轴仍是一个烦杂的计算准备过程，更适用于轴径变化少或转子组件形状复杂的状况。

2.3 接触行为下的有限元仿真分析

2.3.1 罚函数模型求解

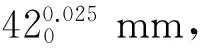
图6 位移检测环与心轴的初始穿透量

罚函数法利用1个弹簧施加接触协调，计算时穿透量xP即接触弹簧的变形量。该穿透量仅用来协调接触方程，并不存在于实际情况，过大的刚度在收敛过程中往往引起振荡，导致收敛困难或无法求解。只要穿透量足够小或可忽略，求解的结果就是精确的。对于柔性弯曲为主的接触问题时，推荐fFKN=0.01～0.1。观察图7中二阶弯曲固有频率的变化，其随着fFKN的不断增加且速度逐渐放缓，是一个趋于稳定值的过程。当fFKN取0.06后，二阶弯曲固有频率的变化不再明显。

图7 固有频率随fFKN的变化趋势

2.3.2 摩擦接触模型求解

增广拉格朗日方法因为额外因子λ，对于接触刚度kNormal的值变得不敏感。初始几何穿透的加载与罚方法相同，区别在于增广拉格朗日方法使用摩擦接触类型，针对不同的摩擦系数μ求解出的固有频率如图8所示。参考材料手册，配重盘与轴的摩擦系数取0.12，检测环等与轴的摩擦系数取0.15。

图8 不同摩擦系数下的固有频率

3 实验数据与仿真结果的对比分析

模态测试通过引入传递函数的概念，通过击振实验，从激励和响应之间的函数关系入手，得到系统的固有特性。采用国产数采仪进行模态击振实验，结合模型修正后的仿真数据如表5所示。

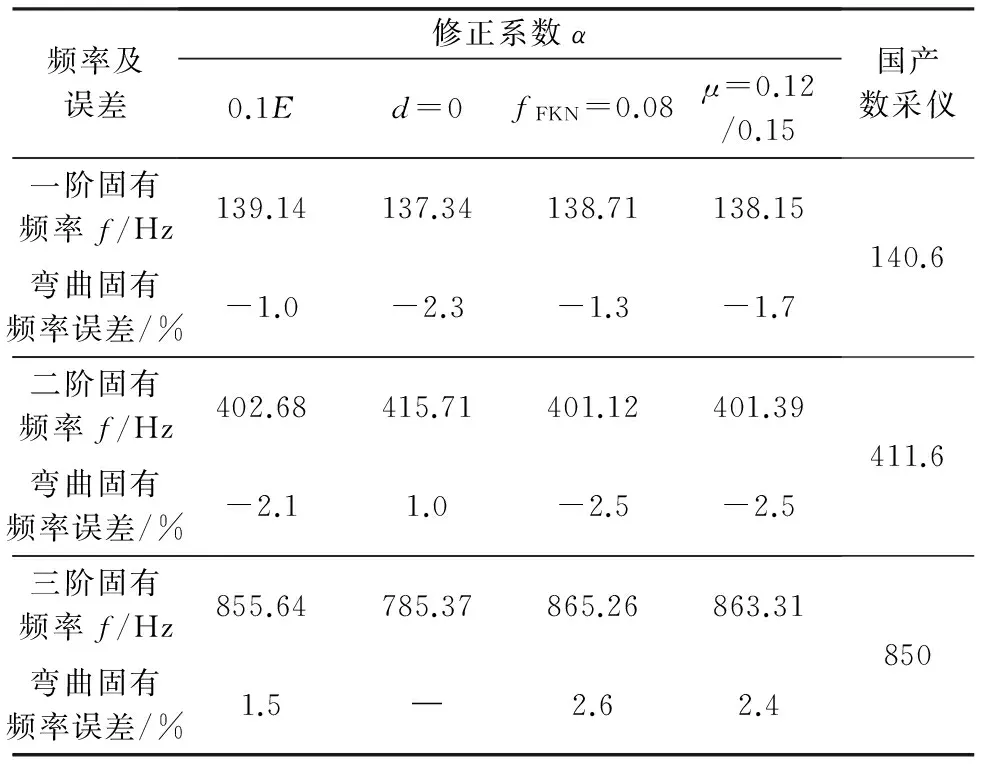
表5 基于模型修正下的固有频率及误差对比

在对弹性模量进行修正的过程中，修正系数0.1较理想，计算结果相对误差不超过2.2%，且对前三阶弯曲固有频率都有较好的预测，且比修正直径便捷。引入接触行为后，有限元模型相对复杂，迭代求解时间长，但保证了模型的完善性，对于预应力下的模态求解，将由配合产生的内应力导入模态求解中，获得了与测试值更接近的结果。

有限元模型越接近于实际，求解结果越可靠。罚函数模型由于采用推荐的接触刚度系数来求解弯曲问题，其模型精确性低于摩擦接触模型。以位移检测环与心轴的配合为例，采用表5中的修正系数，以增广拉格朗日及罚方法计算其接触压力，并结合式(5)的理论计算，结果如图9所示。

图9 轴外表面接触压力分布图

未配合的部分接触压力趋近于0，配合边缘处出现应力集中现象。在50～100 mm的配合部位，摩擦接触模型与理论值更接近，罚函数模型中针对弯曲问题所取的接触刚度系数小(0.01～0.1)，计算出的接触压力较理论值小，即针对弯曲问题优化出的罚函数模型应用范围较窄，依据摩擦接触模型可完成过盈量的设计[9]，并针对不同环境条件对摩擦系数进行调整[10]。

依据表5中修正系数经验，以图10中混合磁悬浮轴承支撑的转子系统为研究对象，该轴的阶梯较多，从网格计算量及收敛性角度考虑，选择对转动惯量修正(修正系数0)，罚函数模型修正(fFKN=0.02)，由于该转子装配体采用轻型压入配合，配合公差H7/p6，借助锁紧螺母固定，相对于一体化加工而言，其抗弯性能大大减弱，忽略局部配合时计算误差较大，结果如表6所示。

图10 混合支撑磁悬浮转子模态测试示意图

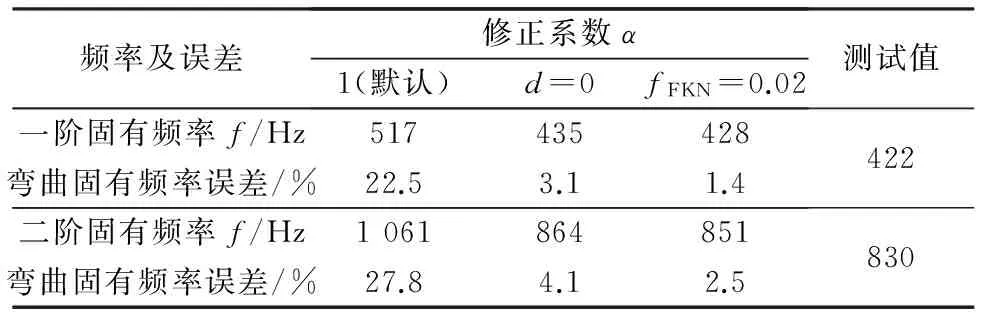
频率及误差修正系数α1(默认)d=0fFKN=0.02测试值一阶固有频率f/Hz517435428弯曲固有频率误差/%22.53.11.4422二阶固有频率f/Hz1061864851弯曲固有频率误差/%27.84.12.5830

4 结 语

过盈联接模型修正方法可应用在轴承、叶轮等转子配合问题上。对于指导结构设计和求解实际工程问题具有一定作用。

1) 通过修正弹性模量来反映过盈配合是一个简单高效的方式，尤其对转子心轴弹性模量修正。转子组件材料修正系数应趋近于0。

2) 针对附加组件转动惯量修正，其存在增加计算准备量而降低求解难度的特点。取修正系数0，将转子组件质量全部附加到心轴上可获得一个较为保守的结果。

3) 接触行为中罚函数求解精度依赖于接触刚度系数，依据弯曲问题推荐的范围(0.01～0.1)，较小的刚度更容易收敛，尝试多次求解并比对数据可获得较理想结果。

4) 从接触压力的角度，结合理论计算说明了摩

擦接触模型的可靠性。相比于罚函数，其不需要针对弯曲问题选择接触刚度系数，应用场合更为广泛。

[1] 汤恩琼,房建成,郑世强.磁悬浮电动机柔性转子振动控制与试验研究[J].机械工程学报,2015,51(1):106-116.

[2] 王继强,王凤翔,宗鸣.高速电机磁力轴承-转子系统临界转速的计算[J].中国电机工程学报,2007,27(27):94-98.

[3] 王洪涛,郭垒磊,万力等.磁力轴承支承刚性转子的临界转速计算[J].中国机械工程,2010(8):904-907.

[4] 苏春峰,艾延廷,娄小宝.接触非线性仿真中接触刚度因子选取的方法研究[J].沈阳航空航天大学学报,2009,26(3):5-9.

[5] HUANG Z,FANG J,WANG K.Dynamics of flexible rotor-shaft assembly with consideration of contact behaviors[J].Journal of Mechanical Engineering Science,2014,229(5):859-868.

[6] CHEN S Y,KUNG C,HSU J C.Dynamic analysis of a rotary hollow shaft with hot-fit part using contact elements with friction[J].Transactions- Canadian Society for Mechanical Engineering,2011,35(3):461-474.

[7] 李伟建,潘存云.圆柱面过盈连接的应力分析[J].机械科学与技术,2008,27(3):313-317.

[8] SCHWEITZER G，MASLEN E H．Magnetic bearings：theory，design, and application to rotating machinery[M] .Birlin:Springer，2009.

[9] 谷家伟,葛云,张立新,等.红花采收机胶辊的装配过盈量设计研究[J].机械设计与制造,2016(5):131-135.

[10] 肖乾,方骏,王磊.摩擦系数对高速列车车轮瞬时滚动接触疲劳的影响[J].中国铁道科学,2016,37(3):68-74.