基于多源数据融合的城市道路网络宏观基本图模型

金 盛，沈莉潇，贺正冰

(1.浙江大学建筑工程学院，杭州310058；2.北京交通大学交通系统科学与工程研究院，北京100044)

0 引言

伴随着城镇化和机动化的快速发展，城市交通拥堵问题已经由节点、干线扩展至整个路网，因此研究区域路网的交通状态就显得尤为迫切.区域交通状态是进行区域交通流建模与管控的重要基础.为了研究以城市道路网为整体的交通流特性，Geroliminis等[1-2]最早定义了路网宏观基本图的概念(Macroscopic Fundamental Diagram,MFD)，认为MFD可描述为路网中在运车辆数和通行能力的关系，并证明了城市路网MFD的存在.在交通不均匀性对MFD在交通状态判别影响的研究方面，Knoop等[3]提出了广义宏观基本图(Generalized Macroscopic Fundamental Diagram,GMFD)描述路网交通状态，将路网通行能力、平均车辆数和密度分布联系起来.在基于不同数据源下的MFD构建研究方面，Gayah等[4]利用手机数据和宏观基本图估计路网密度；Ambühl[5]利用线圈数据和浮动车的数据融合模型构建MFD，利用与临界密度的关系，评价融合模型相对单一数据降低了MFD的误差.

国内也有很多学者陆续开展了MFD及其在区域状态判别和管制方面研究工作.王福建等[6]利用MFD将路网交通状态分级，并提出了针对性的路网管控策略.张逊逊等[7]基于MFD实现路网多子区的协调控制.姬杨蓓蓓[8]采用仿真试验的方法验证了MFD在高速公路、城市主干道和城市道路中的存在性，并论证了路网中关键路段对MFD的影响，认为路网中只要主要道路布设有检测器就能得到较好的路网MFD.贺正冰等[9-10]利用断面检测器数据绘制了北京快速环路的宏观基本图，分析了其“8”字型特征并给出了成因.卢守峰等[11]提出基于流量和出租车GPS数据构建MFD的方法，并发现路网中密度的分布不均匀是导致路网通行能力不高的原因.

MFD可以较直观表征路网的交通流特性，有利于更好地对区域交通进行管控，所以构建准确的MFD具有重要的理论和实际意义.现有的研究大多基于仿真数据、断面检测器或浮动车数据，在构建城市道路路网MFD时仅考虑了路段长度的影响，实际中还与路段车道数相关，本文在计算路网加权流量和密度时，同时考虑了路段长度与车道数的影响.针对我国城市道路检测器布设现状，提出了基于微波数据和车牌识别数据的城市道路宏观基本图构建模型，并提出与路网通行能力、临界密度关系的MFD差异性评价指标，称为状态比.最后，论文以青岛市实际数据对模型进行了验证.

1 MFD模型构建

为了构建符合实际情况的路网MFD，需要充分的数据来估计路网流量和密度.根据MFD理论，采用式(1)进行MFD的计算[2].

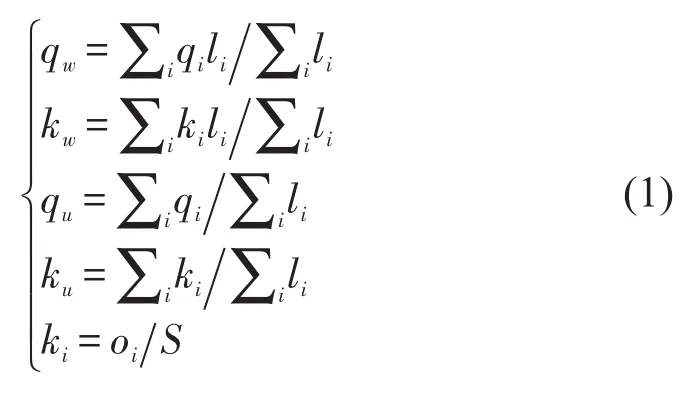
式中：qw、kw分别为路网加权流量(veh/h)和路网加权密度(veh/km)；qu、ku分别为路网无权重流量(veh/h)和密度(veh/km)；qi、ki和oi分别为路段i的流量(veh/h)，密度(veh/km)和占有率；li为路段i的长度(km)；S为平均有效车身长度(km).

本文中采用加权流量和密度构建路网MFD.不同交通检测器得到数据类型不同，其计算方法介绍如下.

1.1 微波检测器数据

利用微波检测器数据(Remote Traffic Microwave Sensor Data,RTMSD)估计路网MFD，RTMSD类型为断面单车道的交通流数据，在计算时需将其整合为断面的数据，以流量加权，计算公式为

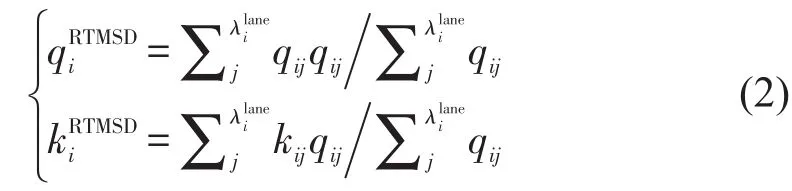
1.2 车牌识别数据

利用车牌识别数据(License Plate Recognition Data,LPRD)可以得到车辆进入路段和驶离路段的行程时间.其计算公式为

根据式(4)得到车牌识别数据下的路段i流量qi与密度ki为

式中：N为统计间隔内过检测器的车辆数；Nma为能够匹配到行程时间的车辆数；T为统计间隔时长.

1.3 路网加权流量和密度

不同路段在路网的重要性不同，对路网交通影响程度也不同，简单理解为路段长度与车道数不同的路段在路网中的地位不同，路段长度越长，车道数越多，可承载的车辆数也多，其对路网通行能力贡献度也就越大，许菲菲等[12]也证明了路网的关键路段一般为路段较长和车道数较多的路段，对MFD影响较大.所以计算路网加权流量(veh/(h⋅ln))与加权密度时，权重取路段长度li和车道数的乘积.

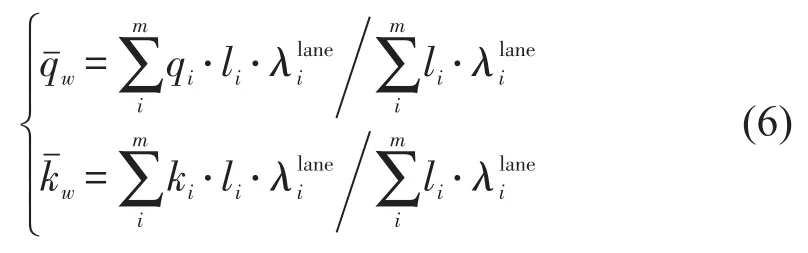
式中：m为路网内能检测到交通流数据的路段数，在实际路网中并不是所有路段都有检测器，所以一般m小于路网的总路段数，但路网主要道路布设有检测器就能得到较好的路网MFD.

通过式(6)计算可以得到关于路网加权流量和加权密度的散点图，为得到路网的临界密度、通行能力、阻塞密度等交通特征值，一般需对上述得到的散点图进行拟合，Knoop等[4]提到MFD可以用很多函数拟合，基于前人的研究，本文假设MFD的形状为二次项的.MFD分布曲线采用两次多项式拟合需满足如下条件：

(1)MFD以临界密度为界可分为两部分，左边表示非拥堵状态，右边表示拥挤状态，所以曲线应存在极值且为正；

(2)MFD中密度为零时流量为零，因此拟合方程常数项为零.

根据上述条件，MFD曲线一般方程为

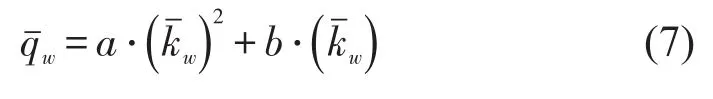
式中：a，b为拟合方程系数.

路网交通状态演化从非拥堵到拥堵的状态点为临界点(qc),kc)，即MFD曲线极值点，根据式(8)求得qc，kc.

2 2种数据源下MFD的差异性

首先假设RTMSD和LPRD构建的MFD都为准确的路网MFD，进行两者差异性比较.我们认为MFD中绝对值与实现网络交通分析、管理与控制等不相关，当两个路网可能具有相似的通行能力或临界密度时，由于交通不均匀性或不同交通行为(如路网达到拥塞时间不同)，所采取的管控措施也不同.所以只考虑绝对值差异，可能会没有实际意义，反而可能导致结果无效或非常不准确.因此，提出采用状态比(Traffic State Ratio，R)来评估MFD，即任意时刻路网交通参数和临界状态的距离比，如图1所示.某一时间间隔的交通状态比可表示路网接近或远离拥堵的距离.根据该方法，完全一样的MFD在每个数据采样间隔可以得到完全相同状态比.

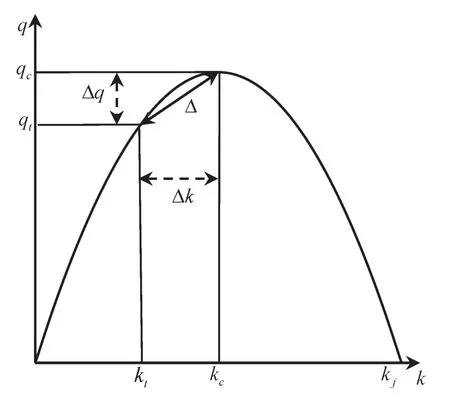
图1 任意时刻状态与最佳状态距离示意图Fig.1 Illustration of distance between traffic state and optimal state

c阻塞密度kj及通行能力qc，我们将状态比R分为非拥堵比run和拥堵比rco，则状态比计算公式如式(9)所示.其中，run,rco∈ (0,1)，两者越接近0，代表路网状态越接近最佳状态；两者越接近1，run表示路网内在运车辆数越少，越接近自由流状态，rco表示路网交通状态越差.

所以MFD的差异性可理解为状态比的差异，则定义Δ为不同数据源下MFD的差异，Δ越大，MFD差异性越大，反之越小.

3 数据融合模型

LPRD和RTMSD都能检测获得路网中的交通流参数.但是由于不同类型交通检测器数据获取方式的不同，检测值会存在较大的差异性.因此，本文提出了基于多源数据融合下的MFD构建方法.该融合算法是基于如下假设：在Δ值较小的情况下，不同类数据源虽然在MFD形状上不同，但反映路网交通状态的变化特性是一致时，将不同类型数据进行融合构建MFD并不会改变其对路网交通状态的判别.

Buisson等[13]研究发现断面检测器的位置对宏观基本图的形状有重要关系，当检测器的位置遍布信号上游、下游及路段中间时，构建的宏观基本图能较好地反应区域交通状态，RTMSD为断面检数据，在构建MFD时假设检测器断面与路段其他断面是同质均匀的.LPRD为路段区间数据，反应进入路段到离开路段整个过程，可以反映包括进口道在内的整个路段的交通状态，可以理解成在路段各断面状态的综合体现.所以基于以下原则建立融合模型：

(1)对于任意路段，若有车牌识别检测器，则利用LPRD计算路段流量和密度；否则，采用RTMSD进行计算.

(2)利用式(6)计算路网加权流量和密度，将路网分成2个子集.

(i)LPRD子集，有LPRD路段集合；

(ii)RTMSD子集，有RTMSD路段集合.

(3)对于两者的权重为α和1-α，，其中，mLPRD为路网中有车牌识别系统的路段，m为路网内布有检测器的路段总数，li为路段i的长度.

每个数据采样间隔t的路网加权流量和密度为

4 实例分析与讨论

选取青岛市市南区3.5 km×2 km区域作为本文研究对象，区域共有67个路段，其中有RTMSD的路段52个，有LPRD路段46个，如图2所示.本文中的路段是指相邻交叉口间区段，1条道路可能包含多个路段.此外，考虑到很多路段在早晚高峰不同方向的交通状态差别较大，所以当路段为双向时，在本模型中记为2条路段.在构建MFD时需要得到不同交通状态下的交通流数据，所采用的车牌识别数据和微波数据为2016年9月1～23日工作日全天的数据，统计间隔为5 min.在数据缺失时采用上一时段数据平滑方法进行补全，计算公式为

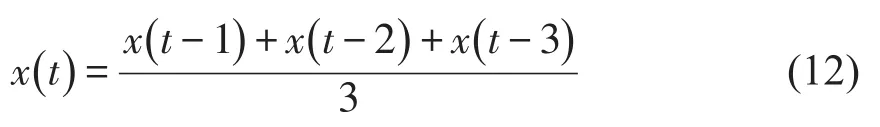
式中：x(t)代表第t个统计间隔的交通流数据.

4.1 构建MFD

利用RTMSD和LPRD，根据式(2)～式(6)计算得到的路网加权流量和密度如图3和图4所示，不难看出两者的趋势基本相同，表示路网交通状态变化的趋势一致.密度和流量出现峰值的时间不同，是因为流量达到最大时对应为临界密度并非最大密度，是路网出现的最大值.

图2 研究区域的路网示意图Fig.2 Illustration of the research network

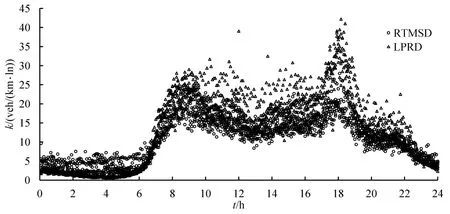
图3 路网加权密度图Fig.3 Network weighted density diagram

图4 路网加权流量图Fig.4 Network weighted flow diagram

基于上述规律，分别得到2种不同数据源下区域流量和密度散点图如图5和图6所示，再根据式(7)拟合得到2种数据源下的MFD，其中图6中出现散点均为9月22日的数据点，是因为这一天某些路段在14:00-17:00存在路段数据缺失的原因造成的.RTMSD在95%置信区间下拟合结果为，其 中 拟 合 优 度R2=0.890 4；LPRD在95%置信区间下拟合结果为，其 中 拟 合 优 度R2=0.847 4.R2＞0.5都成立，认为拟合函数可接受.利用式(8)计算得到：分别为22.8 veh/(km⋅ln)、502.22 veh/(h⋅ln)、27.4 veh/(km⋅ln)和287.76 veh/(h⋅ln).

从图5和图6中，可以看出同一区域根据不同数据源得到的MFD形状不同，路网通行能力和临界密度等特征值也不同，这是因为数据源不同，所反映的特征区间不同，RTMSD主要以微波断面附近交通状态为特征状态代表整个路段状态；LPRD以上下游车牌识别系统围成路段为特征状态，基本包括整个路段.在城市道路中，同一路段上，同一时刻下由于受到交通信号的影响，靠近进口道停车线的车辆车头间距和饱和流量均会略小于路段的，所以2个MFD中表现出LPRD的kc较大，qc较小.

4.2 MFD差异值

根据式(9)和式(10)，计算2种数据源下的状态比R和差异值Δ.由图7可知2种数据下的密度比相近，且变化趋势一致，|Δ|的平均值为0.056，极大值为0.14，认为2种数据源下对路网状态判别一致，在路网存在2种数据源时可以融合计算.

选取路网的主要道路中2种检测器都覆盖较为全面，为了简化并验证融合模型的准确性，从实验路网中随机分为路段总长度相同的2个子集，其中一子集为布设微波检测器的路段，另一子集为布设车牌识别系统的路段，根据融合算法，此时α=0.5，即

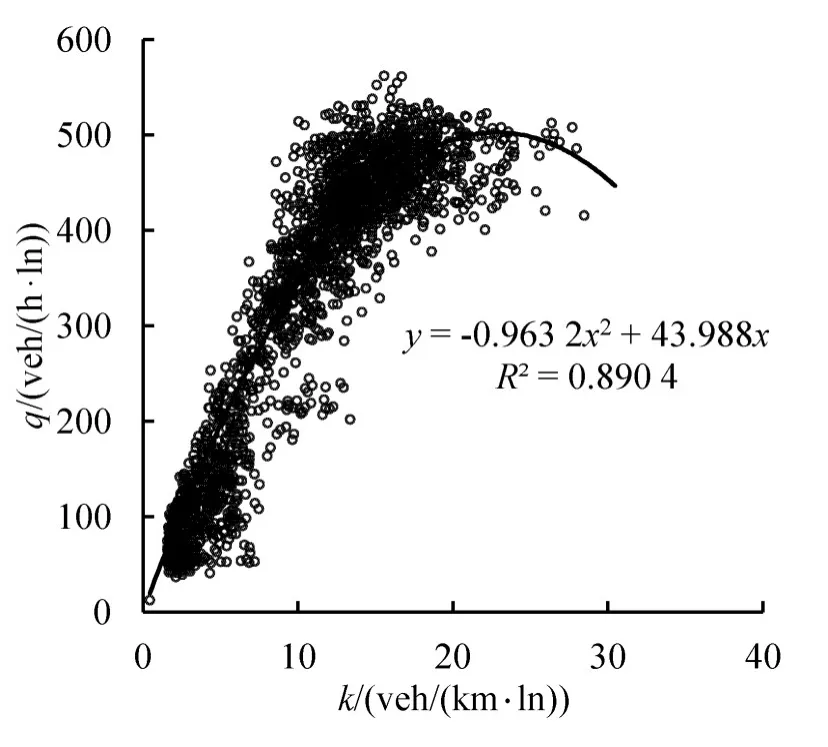
图5 RTMSD的MFDFig.5 The MFD constructed by RTMSD

图6 LPRD的MFDFig.6 The MFD constructed by LPRD

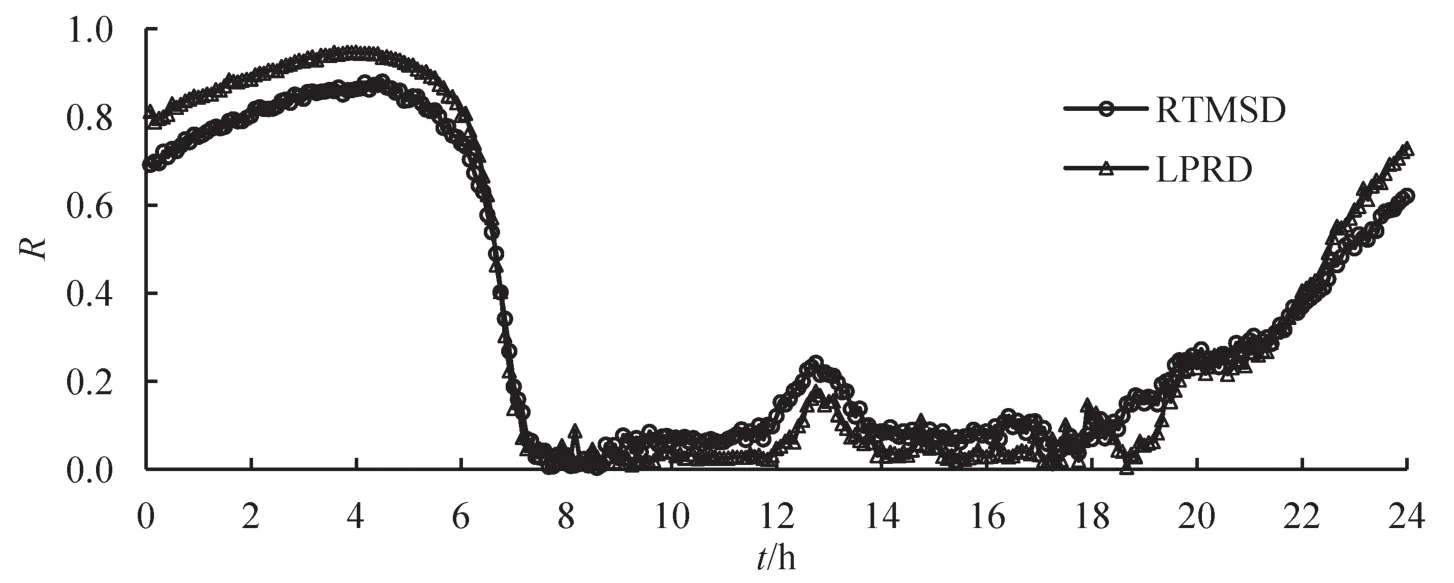
图7 状态比图Fig.7 Traffic state ratio diagram

通过式(2)、式(5)、式(6)及式(13)得到MFD如图 8 所示，拟合结果为其中拟合优度R2=0.957 6，根据式(8)得：和分别为22.657 veh/(km⋅ln)，399.434 veh/(h⋅ln).

图8 融合模型下的MFD图Fig.8 The MFD constructed by fusion data

根据式(9)和式(10)，计算单一数据源下MFD和融合模型下MFD的差异性指标.本文差异值计算时分别以LPRD和RTMSD下状态比为基准，分别如图9，图10，表1和表2所示.从图9和表1中看出，|Δ|的均值和极大值都是融合模型下最小，说明融合模型构建的MFD与LPRD构建的MFD最相近.从图10和表2中同样看出，融合模型构建的MFD的|Δ|均值和极大值均小于单一数据源下覆盖部分路网的.说明数据融合下构建的路网MFD较单一数据源降低了误差.另从图9，图10，表1和表2发现，若利用融合模型中任一子集数据构建的路网MFD表征整个路网MFD，虽误差较检测器覆盖两子集的单一数据源模型和多源数据融合模型增大，但误差基本在0.2之内，即在检测器随机减少50%时误差仍在20%以内，说明在构建路网MFD时对检测器覆盖率要求并不严格.

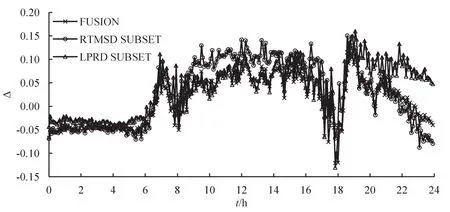
图9 以LPRD为基准的差异性指标图Fig.9 The difference diagram base on LPRD

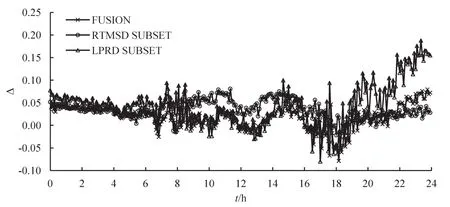
图10 以RTMSD为基准的差异性指标图Fig.10 The difference diagram base on RTMSD

表1 以LPRD为基准的各数据源下MFD的差异值Table 1 The MFDs’difference among each data source base on LPRD

表2 以RTMSD为基准的各数据源下MFD的差异值Table 2 The MFDs’difference among each data source base on RTMSD

5 结论

本文考虑到不同道路特性对MFD的影响，在构建路网MFD时采用路网路段长度和车道数加权进行密度和流量的计算.由于目前我国城市道路中交通流检测器仍以断面检测器为主，仅有部分道路布设了车牌识别系统.因此，研究不同类型数据源下的路网宏观基本图具有重要的理论与现实意义.本文基于利用传统微波断面数据和LPRD数据构建同一路网的MFD，采用状态比来比较两者差异并提出融合模型，具体结论如下：

(1)采用不同类型交通数据源所构建的MFD形状不同，特征值也不同.

(2)引入状态比的概念来评估MFD的差异性，认为每一个时段R越接近，MFD也越接近.研究发现同一路网不同数据源下的R接近，即当路网存在不同数据源的2个子集时，也可融合绘制路网MFD.

(3)融合模型得到的MFD比单一数据源下路网MFD估计误差小.

参考文献：

[1]GEROLIMINISN,DAGANZO CF.Macroscopic modeling of traffic in cities[C].Transportation Research Board 86th Annual Meeting,2007.

[2]GEROLIMINIS N,DAGANZO C F.Existence of urbanscale macroscopic fundamental diagrams:Some experimental findings[J].Transportation Research Part B Methodological,2008,42(9):759-770.

[3]KNOOPV L,HOOGENDOOM S P.Empirics of a Generalized macroscopic fundamentaldiagram for urban freewas[J].Transportation Research Record,2013,2391(1):133-141.

[4]GAYAH V V,DIXIT V V.Using mobile probe data and the macroscopic fundamentaldiagram to estimate network densities[J].Transportation Research Record Journal of the Transportation Research Board,2013(2390):76-86.

[5]AMBÜHL L,MENENDEZ M.Data fusion algorithm for macroscopic fundamental diagram estimation[J].Transportation Research Part C Emerging Technologies,2016(71):184-197.

[6]王福建,韦薇,王殿海,等.基于宏观基本图的城市路网交通状态判别与监控[C].北京:电子工业出版社，2012.[WANG F J,WEI W,WANG D H,et al.Traffic state identification and monitoring of urban network based on macroscopic fundamental diagrams[C].Beijing:Electronic Industry Press,2012.]

[7]张逊逊,许宏科,闫茂德.基于MFD的城市区域路网多子区协调控制策略[J].交通运输系统工程与信息,2017,17(1):98-105.[ZHANG X X,XU H K,YAN M D.Coordinated control strategy for multi-subarea based on MFD in urban zonal road networks[J].Journal of Transportation Systems Engineering and Information Technology,2017,17(1):98-105.]

[8]姬杨蓓蓓，WINNIE D.阿姆斯特丹城市道路线圈检测器布设方法研究[J].重庆交通大学学报(自然科学版),2010,29(5):754-757.[JI Y B B,WINNIE D.Study on the layout method of urban road loop detector in Amsterdam[J].Journal of Chongqing Jiaotong University(Natural Science Edition),2010,29(5):754-757.]

[9]贺正冰,关伟,樊玲玲,等.北京市快速环路宏观基本图特征研究[J].交通运输系统工程与信息,2014,14(2):199-205.[HE Z B,GUAN W,FAN L L,et al.Characteristics of macroscopic fundamental diagram for Beijing urban ring freeways[J].Journal of Transportation Systems Engineering and Information Technology,2014,14(2):199-205.]

[10]HE Z B,HE S,GUAN W.A figure-eight hysteresis pattern in macroscopic fundamental diagrams and its microscopic causes[J].Transportation Letters,2015,7(3):133-142.

[11]卢守峰,王杰,刘改红,等.基于流量和出租车GPS数据的城市道路网络宏观基本图[J].公路交通科技,2014,31(9):138-144.[LU S F,WANG J,LIU G H,et al.Macroscopic fundamental diagrams based on traffic flow and taxi GPS data[J].Highway Traffic Technology,2014,31(9):138-144.]

[12]许菲菲,何兆成,沙志仁.交通管理措施对路网宏观基本图的影响分析[J].交通运输系统工程与信息,2013,13(2):185-190.[XU F F,HE Z C,SHA Z R.Analysis of the impact of traffic management measures on macroscopic fundamental diagram[J].Journal of Transportation Systems Engineering and Information Technology,2013,13(2):185-190.]

[13]BUISSON C,LADIER C.Exploring the impact of homogeneity of traffic measurements on the existence of macroscopic fundamental diagrams[J].Transportation Research Record Journal of the Transportation Research Board,2009,137(2124):127-136.