基于SVR的区域交通碳排放预测研究

陈 亮，王金泓，何 涛，周志华，李巧茹*，杨文伟

(1.河北工业大学土木与交通学院，天津300401；2.天津市绿色交通工程材料技术中心，天津300401；3.广州市交通规划研究院，广州510000)

0 引言

随着工业化发展速度加快和新兴经济体规模的扩大，我国已成为世界上最大的能源生产和消费国，同时也是世界上CO2排放量最大的国家.研究表明，交通运输业是对全国碳排放强度下降和碳排放增长贡献最大的行业之一，且现阶段能源消耗量和碳排放量均呈逐年上升趋势[1].因此，交通运输业应承担起降低碳排放的重要责任.

目前，国内外专家学者关于交通碳排放的研究主要包括两大类：其一，为交通碳排放影响因素分析，多数学者站在整个国家或某具体省市的角度，宏观分析交通碳排放驱动力作用[2-3]；或研究不同交通领域和不同运输结构诸多碳排放影响因素[4]，同时对某一具体指标(如碳排放效率、能源利用率等)变化影响机理的研究也日益增加[5-6].但是我国区域经济发展不均衡，不同省市区域之间的交通碳排放水平存在明显差异，因此单纯从国家或某具体区域角度分析交通碳排放影响因素问题会存在一定局限性.其二，为交通碳排放预测及节能减排策略研究，大部分学者通过构建Kaya恒等式、IPAT或STIRPAT模型及其扩展模型、GM(1，1)模型等来直接预测碳排放总量[7-9]；或是结合线性回归法和情景预测法预测不同情景下的碳排放情况并提出针对性建议[10].但是，传统预测方法存在偏最小二乘回归和岭回归稳定性低、可解释性较弱、关键参数难确定等不足.此外，区域交通碳排放系统为复杂非线性系统，传统预测方法因缺乏数据样本学习过程而导致非线性关系模糊，计算过程复杂，预测结果精度降低.

综上所述，本研究综合考虑我国区域发展特征和交通碳排放研究现状，借鉴STIRPAT模型中各影响因素的选取方法并对其进行扩展，选择具有区域特征的碳排放影响因素分析我国区域交通碳排放变化规律；同时，为避免传统预测方法的诸多弊端，构建支持向量回归机(Support Vector Regression,SVR)模型对我国区域交通碳排放进行预测.该模型可有效解决预测模型中小样本、非线性等问题，且在高维模式识别中表现出一定优势，因此在行业碳排放预测方面具有良好的实用性[11]，可为交通碳排放预测提供新的科学方法.

1 影响因素选取和模型建立

1.1 碳排放影响因素选取

STIRPAT模型是由York等提出的关于人口、富裕和技术对环境的随机影响模型，为提高模型的分析解释能力，模型各因素均可进行扩展改进[3].交通碳排放主要影响因素包括交通自身影响、经济发展和科学技术3个方面[3]，因此选取旅客周转量、货物周转量、人均GDP、机动车保有量、碳排放强度、能源结构和城市化率能源效率7项影响因素作为交通碳排放预测自变量.其中，货物周转量和旅客周转量反映交通自身影响，人均GDP和机动车保有量反映社会富裕程度影响，碳排放强度和能源结构反映交通运输业科技发展水平影响，城市化率作为扩展项用来反映区域特征.

碳排放强度是单位GDP所产生的碳排放量，用来反映经济增长与碳排放之间的关系.计算方法为

式中：I为碳排放强度；Ct为历年交通运输行业碳排放总量；Gt为历年经济生产总值.

关于能源结构，本文借鉴产业结构指数构造法，将其定义为不同能源(本文重点研究电力和天然气两类清洁能源比例)消耗转换标准煤用量与行业消耗能源标准煤总量的比值，计算方法为

式中：R为不同能源消耗所占比例；Ei为第i种能源消耗量；ci为第i种能源转换标准煤系数[12].

1.2 预测模型建立

1.2.1 支持向量回归机

支持向量回归机是一种基于SVM思想，利用统计学习理论进行回归计算的机器学习法[13].该方法适用于有限样本研究，可在理论上得到全局最优解，且计算过程复杂程度与样本维数无关，在函数逼近、回归预测等方面可达到最优效果.本研究选择ε-SVR模型进行区域交通碳排放预测，具体步骤如下：

给定线性训练集为

式中：xi为输入向量；y为输出值.

设Rn上的一个线性函数表达式为

式中：ω为权值向量；b为偏移常量.

依据数理统计学理论，函数估计问题可转化为式(5)和式(6)的最优化问题.

式中：ε为不敏感损失系数.

由于个别数据在ε精度下不能完成估计，故引入松弛变量ξi和，将优化过程式(5)转化为式(7).

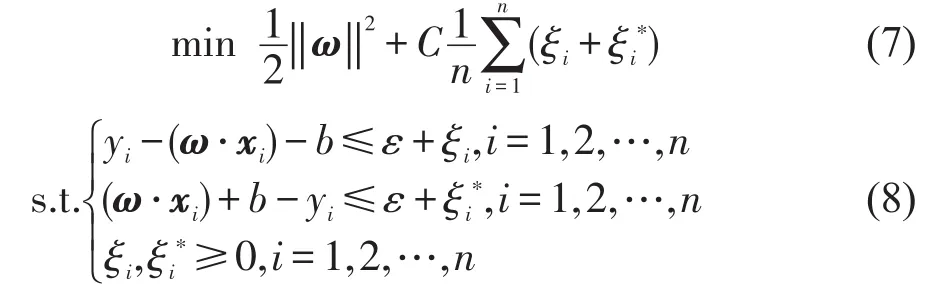
式中：C为惩罚系数.

为便于求解，通常引入拉格朗日乘子α和α*，将模型转换为其对偶问题.

对应的线性回归函数表达式为

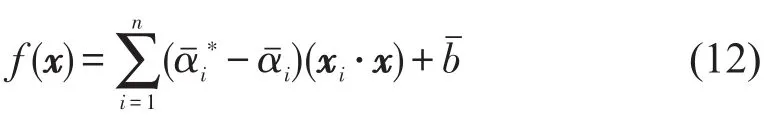
引入核函数K(xi,yi)，将线性问题转化为Hilbert空间中的非线性回归问题，构建ε-SVR模型为

1.2.2 基于ε-SVR的交通碳排放预测模型

获取n年某区域交通碳排放及各项交通碳排放影响因素数据组成样本集，i=1,2,…,n，构建区域交通碳排放SVR模型.具体步骤如下：

(1)对自变量和因变量进行归一化处理，保证所有数据在[0,1]之间.

(2)在样本集中选取m个样本组成训练样本集，剩下n-m个样本组成测试样本集.选择K(xi,x)=exp(-γ‖‖xi-x2)为径向基核函数处理训练样本集，构建ε-SVR模型.设定ε的初始值，应用格搜索和交叉验证法确定参数C和γ的取值，最终得到最优参数ε∗、C∗和γ∗.

(3)对训练样本集数据进行仿真，得到模型最优解和回归函数f(x)，将训练样本集和测试样本集的全部数据分别代入函数输出拟合值，并对拟合结果与真实值进行线性回归，依据相关系数结果判断模型的学习推广能力.若模型学习推广能力差，需返回步骤(2)直到获得最优解.

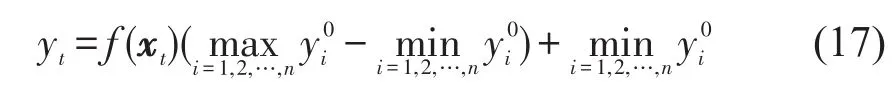
2 数据来源与实例分析

2.1 数据来源

以北京市为例进行实例分析，所研究的交通运输业为交通运输、仓储及邮政业3个行业的综合.所有数据均来源于《中国能源统计年鉴》《北京市统计年鉴》，样本区间为1990—2016年；所涉及的人均GDP、碳排放强度指标均为参照1990年可比价重新计算的结果.

表1 交通碳排放及其影响因素数据Table 1 Data of carbon emissions and influence factors of transportation

2.2 MATLAB运行结果及回归分析

依照ε-SVR预测模型构建步骤，对27年样本数据进行归一化处理.随机选取13年样本数据组成训练样本集，剩余14年数据样本组成测试样本集.运用MATLAB 7.0处理相关数据，设置ε的初始值为0.01，C和γ的取值范围均是[2-8，28]，网格宽度为0.8，采用5折交叉验证法处理训练样本集数据.系统对C的取值范围进行离散化处理，取不同的离散值使得支持向量回归机的训练误差最小，图1为参数选择效果3D图.最终得到C∗为48.502 9，ε∗为0.006 801，交叉验证均方误差(MSE)为0.008 040.

对训练样本集和测试样本集数据进行拟合分析，得到反归一化后的预测值与实际值线性回归结果如图2和图3所示.其中，训练结果线性回归方程为Q=0.963 0M+58.308 9，相关系数为0.984 2，均方误差为0.002 369；测试结果线性回归方程为Q=0.951 8M+66.107 4，相关系数为0.995 0，均方误差为0.001 164.对应预测值与实际值数据对比结果如图4和图5所示，可见模型具有良好的学习推广能力，可用作区域交通碳排放预测研究.

图1 参数选择效果图(3D)Fig.1 The effect drawing of the paramater selection(3D)

图2 训练样本集回归结果Fig.2 Linear regression of the training set

图3 测试样本集回归结果Fig.3 Linear regression of the testing set

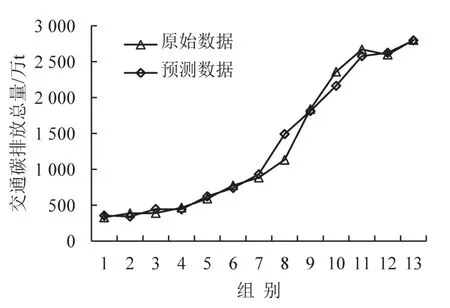
图4 训练预测值与实际值对比结果Fig.4 Forecast and actual values comparison of training set

2.3 未来交通碳排放预测

2.3.1 影响因素预测分析

根据北京市统计局相关数据、北京“十三五”发展规划纲要、北京“十三五”交通发展规划、北京“十三五”能源发展规划、北京市政府统计公报及政府年度工作报告等相关数据，对北京市2017—2020年交通碳排放7项影响因素值进行整理和预测分析.

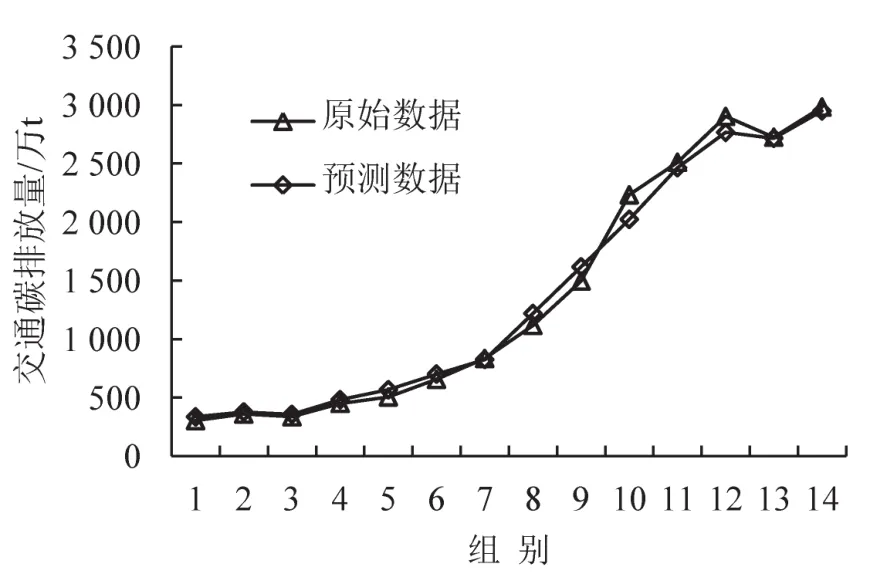
图5 测试预测值与实际值对比Fig.5 Forecast and actual values comparison of testing set

(1)客、货物周转量.

2016年北京市客、货物周转量分别为1 889.31亿人公里和671.33亿吨公里，样本数据年均增长率分别为11.2%和3.6%.预测2017—2020年北京市客、货运周转量分别为2 100.92、2 336.22、2 597.88、2 888.84 亿 人公里和 695.50、720.53、746.47、773.35亿吨公里.

(2)人均GDP.

北京“十三五”发展规划纲要明确提出，到2020年北京市人口总数预测控制在2 300万人之内，年均增长率为1.16%；GDP年均增速保持在6.5%，不低于6%.因此，综合考虑北京市政治重要性、经济发展水平现状及中心产业转移政策等因素，设置预测年限GDP增长率分别为6.0%、6.5%、7.0%，对应年份人均GDP如表2所示.

表2 不同GDP增速下的人均GDP预测值Table 2 Forecast per capital GDP under different GDP growth rate

(3)机动车保有量.

北京交通“十三五”规划中明确提出，预期到2020年北京市机动车保有量控制在630万辆以内，最大年均增长率为2.5%.样本数据增长率最小值为0.5%，因此本文将机动车保有量增长率设置为0.5%、1.5%、2.5%，对应年份机动车保有量如表3所示.

表3 不同增速下的机动车保有量预测值Table 3 Forecast vehicle population under different growth rate

(4)碳排放强度.

碳排放强度是衡量交通运输业科技发展水平的指标之一，由历史数据可知其年均降低比例为6.0%，预测2017—2020年交通碳排放强度分别为0.112 6、0.105 9、0.099 5和0.093 5 t/万元.

(5)能源比例.

北京市交通“十三五”规划明确指出，到2020年北京市交通运输业能耗增长率将控制在6.2%之内，而清洁能源消费比例将继续提升.由样本数据可知，2016年北京市交通运输业标准煤消耗量为1 312.69万t，清洁能源转换为标准煤的消耗量为219.56万t且年均增长率为10.82%.预测2017—2020年清洁能源比例分别为17.45%、18.25%、19.09%和19.97%.

(6)城市化率.

2016年北京城市化率为86.50%，年均增长率为0.63%，预测2017—2020年北京城市化率分别为87.04%、87.59%、88.15%和88.70%.

2.3.2 交通碳排放预测分析

由不同情境下的预测结果(表4)可知，同一GDP增速下，机动车保有量增长率越低，交通碳排放总量越少，说明努力控制机动车保有量的增加，可有效缓解交通碳排放压力；相同机动车保有量增长率条件下，交通碳排放量随着GDP增长速度加快逐渐增大，即一味追求经济发展会带来更多交通运输业的减排压力；随时间推移，交通碳排放总量增长趋势渐缓，年均增长率由9.20%下降到6.12%，说明在相关部门的综合治理下，低碳节能是社会发展的必然趋势.

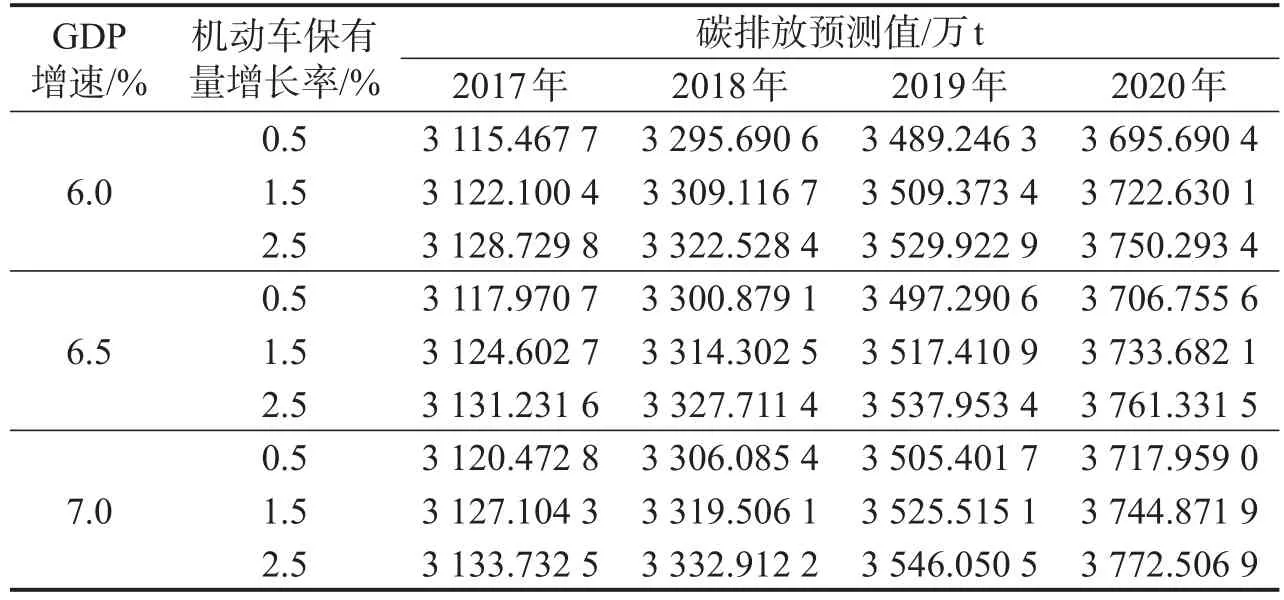
表4 不同条件下的碳排放预测值Table 4 Forecast value of carbon emissions under different situations

3 结论

基于IPCC清单指南的相关数据，确定区域交通碳排放相关指标的测算方法和预测模型，并以北京市为例进行实证分析，得出以下结论：

(1)建立支持向量回归机模型对区域交通碳排放进行预测研究，以北京市为例，交叉验证均方误差仅为0.008 040，训练和测试拟合相关系数分别为0.984 2和0.995 0，均方误差分别为0.002 369和0.001 163，可见模型具有很好的学习和推广能力.

(2)通过预测结果可知，区域交通碳排放总量整体呈上升趋势，社会仍然面临较大温室气体减排压力；但随时间推移，交通碳排放总量增长趋势逐渐变缓，这表明政府节能减排目标已初见成效.以北京市为例，到2020年碳排放总量平均增长到3 733.969 0万t，年均增长率则由9.20%下降到6.12%.

参考文献:

[1]LIN B,XIE C.Reduction potential of CO2,emissions in China׳s transport industry[J].Renewable&Sustainable Energy Reviews,2014(33):689-700.

[2]DARIDO G,TORRES-MONTOYA M,MEHNDIRATTA S.Urban transport and CO2,emissions:some evidence from Chinese cities[J].Wiley Interdisciplinary Reviews Energy&Environment,2014,3(2):122-155.

[3]陈亮,何涛,李巧茹,等.区域交通碳排放相关指标测算及影响因素分析[J].北京工业大学学报,2017,43(4):631-637.[CHEN L,HE T,LI Q R,et al.Index calculation and effect factor study of regional transport carbon emission[J].Journal of Beijing University of Technology,2017,43(4):631-637.]

[4]WANG T,LI H,ZHANG J,et al.Influencing factors of carbon emission in China's road freight transport[J].Procedia-Social and Behavioral Sciences,2012(43):54-64.

[5]卢建锋,傅惠,王小霞.区域交通运输业碳排放效率影响因素研究[J].交通运输系统工程与信息,2016,16(2):25-30.[LU J F,FU H,WANG X X.Research on the impact of regional transportation emissions efficiency factors[J].Journal of Transportation Systems Engineering and Information Technology,2016,16(2):25-30.]

[6]宋震,丛林.中国交通运输业能源效率及其影响因素研究[J].交通运输系统工程与信息,2016,16(1):19-25.[SONG Z,CONG L.Energyefficiencyand influencing factors of Chinese transportation industry[J].Journal of Transportation Systems Engineering and Information Technology,2016,16(1):19-25.]

[7]刘鸿远.城市交通碳排放预测与发展模式选择[D].天津:天津理工大学,2014.[LIU H Y.The forecast of carbon emission of urban transportation and choice of development mode take Tianjin as an example[D].Tianjin:Tianjin University of Technology,2014.]

[8]KAYA Y.Impacts of carbon dioxide emission control on GDP growth:interpretation of proposed scenarios[R].Paris:Presentation to the Energy and Industry Subgroup,Response Strategies Working Group,IPCC,1989:1-25.

[9]YORK R,ROSA E A,DIETZ T.STIRPAT,IPAT and ImPACT:analytic tools for unpacking the driving forces ofenvironmentalimpacts[J].EcologicalEconomics,2003,46(3):351-365.

[10]刘建翠.中国交通运输部门节能潜力和碳排放预测[J].资源科学,2011,33(4):640-646.[LIU J C.Energy saving potential and carbon emissions prediction for the transportation sector in China[J].Resources Science,2011,33(4):640-646.]

[11]宋杰鲲.基于支持向量回归机的中国碳排放预测模型[J].中国石油大学学报（自然科学版）,2012,36(1):182-187.[SONG J K.China’s carbon emissions prediction model based on support vector regression[J].Journal of China University of Petroleum(Edition of Natural Science),2012,36(1):182-187.]

[12]WOOLF D,AMONETTE J E,STREETPERROTT F A,et al.Sustainable biochar to mitigate global climate change[J].Nature Communications,2010,1(5):56.

[13]CORTES C,VAPNIK V.Support-vector networks[J].Machine Learning,1995,20(3):273-297.