架桥机跨武广高速铁路时的抗风稳定性研究

2018-04-26刘树堂

铁道科学与工程学报 2018年4期

刘树堂

(中铁十四局集团有限公司，湖南长沙 410000)

中铁十四局承担长株潭综合Ⅱ标预制箱梁的架设工作，其中株洲醴潭高速立交特大桥(中心里程DK33+815.131)采用32 m简支箱梁斜跨越武广客运专线的水桶坝特大桥。醴潭高速立交特大桥与武广客运专线水桶坝特大桥的平面关系如图1所示。所采用的 32简支箱梁为梁场预制，利用架桥机整体架设的施工工艺。而在架设株洲醴潭高速立交特大桥7号~8号墩时，架桥机下导梁需过孔到8号~9号墩上方，此时架桥机的下导梁正好处于武广客运专线的水桶坝特大桥上方，下导梁与武广客运专线行车轨道板顶面的净距为11.377 m。在开始架设箱梁之前，必须对架桥机工作期间的安全稳定性进行计算。特别是下导梁伸出落在8号~9号墩上方工作期间，此时架桥机下导梁的稳定性除了考虑结构强度与刚度之外，还应考虑强侧风与列车运动风共同作用下的抗倾覆稳定性。列车风对周围桥梁或建筑物产生的气动力大小取决于列车运行的速度、离列车侧面的距离、列车外形及强侧风环境等因素。目前，国内外对于高速铁路沿线建筑物的研究主要集中在列车通过时所引起的结构振动以及减振措

施[1−2]，对跨线桥梁表面的气动压力研究以车桥距离和列车速度的影响为主[3−6]。高速列车运行时所产生的列车风对正上方架桥机下导梁的气动力及迎风面、背风面的风压分布以及对下导梁的抗倾覆性的影响不可忽略。本文借助计算流体力学Fluent软件为仿真平台，采用“动网格”技术和编写UDF列车运动程序，对下导梁处于强侧风和高速列车以不同方式运行所产生的列车风共同作用下的气动环境进行数值模拟，通过多工况的计算来研究了强侧风下和列车风共同作用下，架桥机下导梁的气动力性能及其本身的抗倾覆稳定性，为施工单位架桥机的安全稳定性评估提供最直接的依据。

图1 架设箱梁与武广客运专线关系示意图Fig. 1 Relationship between the railway and box-bridge

1 计算模型及相关参数设置

1.1 几何模型

首先用gambit软件建立车、桥和导梁的几何模型。武广客运专线运行的高速列车为CRH3动车组，为避免计算区域过大以及计算网格数量巨大的问题，将列车进行简化处理，忽略受电弓、轮轨、转向架以及门窗的影响。考虑到中间车具有相似的特性，目前，国内外大多采用简化后的3列车辆模型。本文经过多次试算最后确定采用头车(25.25 m)+中间车(4 m)+尾车(25.25 m)的3节列车模型[7]。列车模型总长54.5 m，宽3.265 m，高3.817 m，并对列车表面做光滑的曲面处理。同样为节省计算资源和计算时间，武广客运专线的水桶坝特大桥几何模型采用5跨32 m的标准简支箱梁；架桥机下导梁的几何模型简化为矩形截面并做光滑壁面处理，下导梁总长为36.5 m，高2.1 m，宽1.7 m，自重432.78 kN，导梁与客运专线及列车运行方向斜交67°；列车头车的鼻尖距下导梁的水平距离为20 m，强侧风运动方向与导梁成90°夹角。

图2 高速列车−桥梁−导梁系统气动力计算模型Fig. 2 Computational model of high-speed train-bridge-system for aerodynamic force

1.2 计算域及网格划分

以5跨32 m简支箱、CRH3列车及下导梁的简化几何模型为对象，建立CFD三维数值分析模型。计算区域以区域内流场分布特征量流速、压力为目标按照单参数逐一优化方法[8]确定。通过反复的试算，在能够满足计算结果的精度的情况下，选取240 m×60 m×264 m的计算区域。由于高速列车几何形状复杂，故流场内采用非结构化的四面体网格进行划分，对列车、桥梁及下导梁的近壁面采用壁面函数法加密网格，列车与桥梁的网格如图3所示。整个区域内网格划分采用放射性网格，即贴近高速列车、箱梁及下导梁断面的网格足够小，而远离这些断面的区域可以适当放大。区域内网格的最小单元尺寸为 0.1 m，整个计算域划分的网格单元总数为245万。列车的运动通过编制UDF程序来实现。列车在运动时，由于网格变形导致网格质量低于特定值时，通过使用局部网格重构(Local remeshing Methods) 和光滑(Smoothing Methods)动网格功能对局部的低质量网格进行更新，以保证列车运动时刻网格的质量和计算结果的精度。计算区域与整体坐标系如图4所示。

1.3 边界条件及计算参数设置

计算区域流场入口采用速度入口边界条件，流场出口采用静压为 0 Pa的压力出口边界条件，桥梁、列车及导梁的表面及计算域上下边界选择光滑无滑移壁面边界。强侧风的马赫数小于 0.3，计算按不可压缩非定常流动问题处理[9]。压强速度关联算法采用稳定性好的SIMPLE算法，湍流模型采用RNG κ−ε模型，选用基于压力的隐式求解方法计算。根据文献[10]入口风速取为25.6 m/s，湍流度为5%，本次计算按照非稳态计算，总时长为1.2 s，时间步长为0.001 5 s。当监控指标三分力曲线平稳且残差达到收敛精度(1.0×10−4)时，认为计算收敛，迭代结束。

图3 列车与桥梁网格图Fig. 3 Mesh of train and bridge grid figure

图4 计算区域及整体网格分布图Fig. 4 Computational domain and mesh of calculation

2 导梁的侧倾力矩

下导梁除了本身的自重外，在强侧风与列车风带来的气动力作用。下导梁在强侧风下发生倾覆，主要是下导梁的侧力、升力和两者共同产生的侧倾力矩过大造成的，其中的侧倾力矩是衡量结构物横风稳定性最重要的指标[11]。通过计算可知，在列车不同运行方式中下导梁的侧倾力矩会发生改变，因此下导梁的稳定性发生变化，如图5所示，研究中先对下导梁几何中心提取侧倾力矩Mz，然后将力矩作用点转移到支点上，可以表示为：

式中：yFxΔ·，xFyΔ·和xG Δ·分别为侧力、升力和自重对导梁支点产生的力矩。

图5 侧倾力矩作用示意图Fig. 5 Diagram of rolling moment

3 计算工况及测点布置

3.1 计算工况

主要对下导梁在强侧风与列车风下的气动力进行计算，根据列车运行方式的不同共设置表1所示的4种工况，即：无列车运行、1列列车运行以及2列列车同时运行，下导梁周围的压力场和风速场变化情况。

表1 列车行驶对下导梁结构风压分布的影响分析工况Table1 Calculation conditions of wind environment

3.2 风压监测点的位置选取

为观察列车从下方经过时，导梁表面的风压变化情况，选取导梁位于线路中央的截面为观测截面此截面底板、截面迎风侧以及背风侧各3个观测点，如图6所示。

图6 导梁表面风压监测点Fig. 6 Locations of pressure-monitoring point

4 计算结果分析

4.1 列车风下的导梁气动力

列车以不同方式经过下导梁时，下导梁的气动力如图 7所示：1)当头车的车头(车身截面变化段)完全经过导梁正下方向时，导梁的侧力最大，相应的侧倾力矩也最大。工况2与工况3中，导梁的侧力对称，工况4中导梁的侧力为0。2)列车的车头完全经过导梁正下方向之前，导梁受到升力为正，头车的鼻尖经过导梁正下方向时，导梁向上的升力最大。尾车的鼻尖离开导梁位置之前，导梁受到升力为负，尾车的车头进入导梁正下方向时，导梁向下的升力最小。工况4中由于2列列车共同作用，导梁升力值约是工况2与工况3中的2倍。

图7 导梁气动力随鼻尖距导梁距离的变化曲线Fig.7 Changing curve of aerodynamic force of the launching nose with the distance between the train and the launching nose

4.2 导梁的侧倾力矩

在4种工况下，下导梁侧倾力矩的计算结果如表 2~3所示。计算结果显示：1)下导梁在 25.6m/s的强侧风和列车风共同作用中，其侧倾力矩中强侧风作用占主导地位，约占92.5%~96.8%，而列车风作用只占3.2%~7.5%。2)在上述的4种工况中，导梁的侧倾力矩Mzl为正且Mzr为负，即表明在25.6 m/s的强侧风和列车风共同作用下，下导梁不会发生侧倾。

表2 强侧风作用下导梁的侧倾力矩Table 2 Rolling moment of launching nose under the action of strong crosswind

4.3 导梁跨中截面风压分布

由表3可知，在工况2中导梁侧倾力矩的绝对值最大，工况2中导梁跨中截面处各测点列车风压极值如表4所示，列车风压分布曲线如图8所示。由表4和图8可知：1)导梁迎风侧不同标高处沿水平方向列车风压分布从梁底向梁顶板逐渐递减。a-3点最大正压、负压分别衰减为a-1点处的58.5%和80.7%。2)同理，导梁背风侧，b-3处的列车风最大正压、负压分别衰减为b-1处的47.6%和78.8%。3)导梁底面垂直方向的列车风压最大正压、负压值基本相等，这是导梁宽度相对较小的缘故。

表3 强侧风与列车风共同作用下导梁的侧倾力矩Table 2 Rolling moment of launching nose under the combined effects of the train-wind and strong crosswind

表4 跨中截面各测点列车风压极值Table 4 Extreme pressure values of the mid-span section

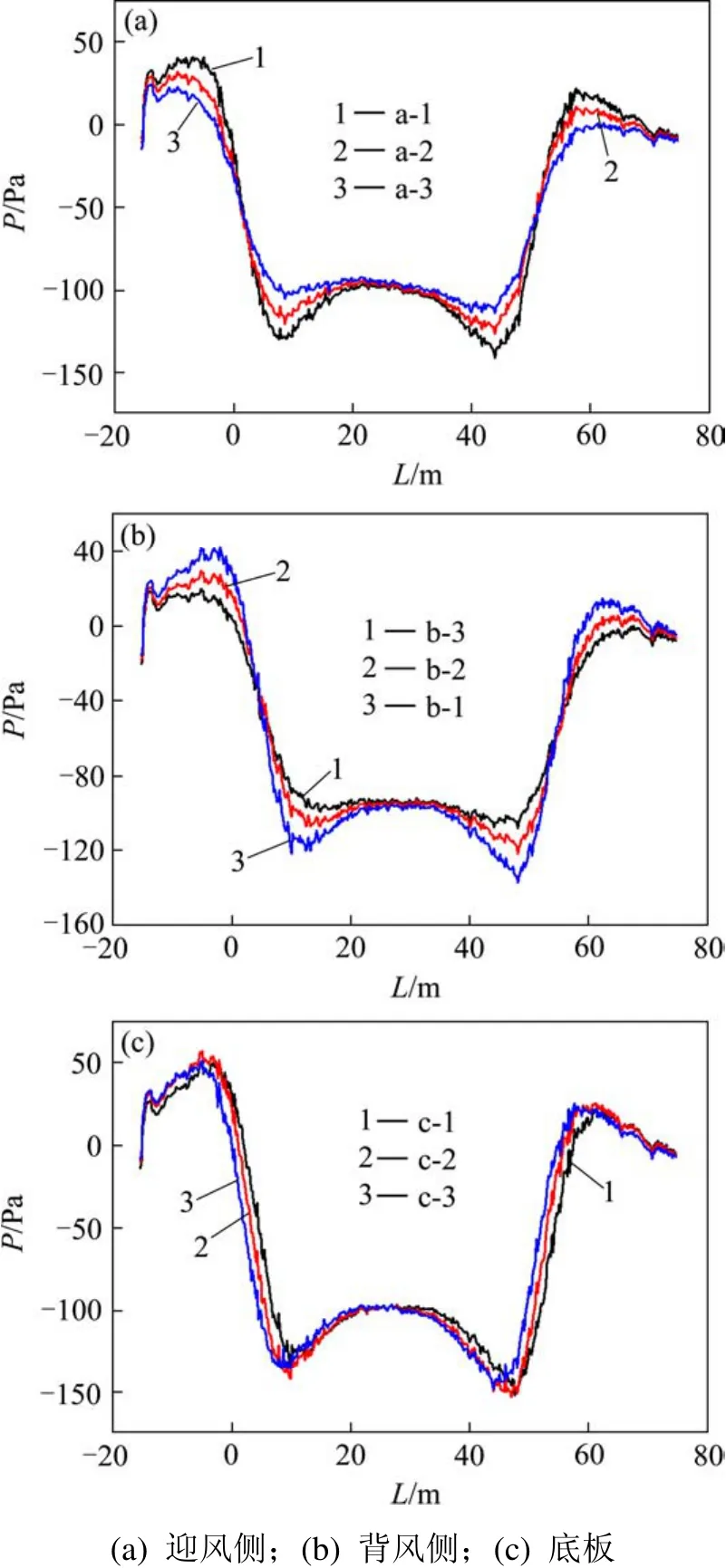
图8 工况2各监测点的风压随鼻尖距导梁距离的变化曲线Fig.8 Changing curves of pressure with the distance between the train and the launching nose

4.4 流场特性分析

为了研究列车风作用导梁的机理，在工况2中导梁取列车正上方的横截面，分析列车鼻尖距下导梁不同距离时其速度分布和压强分布等流场特性的差异。

图9 速度分布云图与气流流线图Fig. 9 Contour of velocity distribution and the streamline chart of air

速度分布云图与气流流线图如图9所示。由图9可知：1)头车鼻尖位于导梁正下方，导梁迎风侧附近的气流水平向下运动，底板与背风侧的气流水平向前运动。2)中车中间段位于导梁正下方，导梁周围的气流水平斜着向上运动，顶板与底板附近的气流速度可达0.9 m/s。3)尾车鼻尖位于导梁正下方，导梁迎风侧的气流斜向上运动，遇到导梁之后水平方向向前运动。导梁底板附近的气流斜着向上，越过导梁底板后，气流斜着向下运动。

静压分布云图如图 10所示。由图 10可知：1)头车鼻尖位于导梁正下方，导梁迎风侧与底板静压为正，顶板与背风侧附近的静压为负，静压值很小，迎风侧正压与背风侧负压对导梁侧面的面积积分叠加得到水平向右的侧力，导梁的升力向上。2)中车中间段位于导梁正下方，导梁周围的静压为负，且大小相近，因此导梁的侧力矩为零，而且导梁升力也基本为 0。3)尾车鼻尖位于导梁正下方，导梁周围的静压为负，且导梁顶板与背风侧静压绝对值较背风侧与顶板的大。迎风侧与背风侧的静压对导梁侧面的面积积分叠加得到水平向左的侧力，同理导梁升力向下。

图10 静压分布云图Fig. 10 Contour of static pressure distribution

5 结论

1) 在强侧风与列车风共同作用下，下导梁的气动力强侧风占95%以上，而列车风的作用可以忽略不计。

2) 当列车运行方向跟强侧风运动方向一致时，下导梁的侧力及侧倾力矩最大；反之，下导梁的侧力及侧倾力矩最小。

3) 导梁表面的气动性与测点至下轨道顶面的距离有关；距离越近，风速值、风压值就越大，反之就越小。

4) 列车风经过导梁时，先是水平向下运动，接着收到挤压而向上运动，最后因为列车的拖拽作用水平向下运动。头车鼻尖位于导梁正下方时，列车风与强侧风作用的方向相同，导梁的侧力及侧力矩增大；尾车鼻尖位于导梁正下方时，导梁的侧力及侧力矩变小。

参考文献：

[1] 杨亦军, 王庆云, 林志兴. 高速列车通过时跨线钢板梁桥的风致振动及其对策研究[J]. 世界桥梁, 2005(1):46−49.YANG Yijun, WANG Qingyun, LIN Zhixing. Research of wind- induced vibration of steel plate girder overhead bridge and measures against vibration thereof due to high-speed running train[J]. World Bridges, 2005(1):46−49.

[2] 尹国高, 张高明, 李敬学, 等. 京沪高铁徐州东站旅客人行天桥振动研究[J]. 建筑结构, 2014, 44(1): 53−57.YIN Guogao, ZHANG Gaoming, LI Jingxue, et al.Vibration study of passenger footbridge in Xuzhou East Station of Beijing-Shanghai high-speed railway[J].Building Structure, 2014, 44(1): 53−57.

[3] 陈玥. 高速列车气动作用及其对跨线斜拉桥的影响研究[D]. 长沙: 中南大学, 2013: 73−80.CHEN Yue. Study of aerodynamic effect of high-speed passing train and its effect on the cable-stayed bridge crossing the line[D]. Changsha: Central South University,2013: 73−80.

[4] 雷波, 刘应清. 高速列车作用在跨线天桥上风压力的数值模拟[J]. 西南交通大学学报, 1999, 34(3): 259−262.LEI Bo, LIU Yingqing. The numerical simulation of the cross-line pressure which was induced by high-speed train[J]. Journal of Southwest Jiaotong University, 1999,34(3): 259−262.

[5] 张建, 杨娜, 郑修凯, 等. 高速列车经过时跨线天桥表面风压小波分析[J]. 振动与冲击, 2015, 34(4): 53−58.ZHANG Jian, YANG Na, ZHENG Xiukai, et al. Wavelet analysis for surface wind pressure of an over-line bridge during high-speed train passage[J]. Journal of Vibration and Shock, 2015, 34(4): 53−58

[6] 闫斌, 陈玥, 戴公连. 高速列车气动力作用下跨线铁路斜拉桥及桥上轨道结构的动力响应[J]. 中国铁道科学,2014, 35(5): 24−27.YAN Bin, CHEN Yue, DAI Gonglian. Dynamic response of fly-over cable-stayed bridge and bridge deck track structure under aerodynamic force of high-speed train[J].China Railway Science, 2014, 35(5): 24−27.

[7] Baker C J. Train aerodynamic forces and moments from moving model experiments[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1986, 24:227−251.

[8] 宋瑞斌. 高速列车通过桥梁时相互气动性能的数值研究[D]. 长沙: 中南大学, 2011: 18−19.SONG Ruibin. The numerical study of aerodynamic characteristics of each other when high-speed train move on bridge[D]. Changsha: Central South University, 2011:18−19

[9] 吴建民. 高等空气动力学[M]. 北京: 北京航空航天大学出版社, 1992: 39−54: 164−174.WU Jianmin. Advanced aerodynamics[M]. Beijing:Beihang University Press, 1992: 39−54: 164−174.

[10] JTG/T D60-01—2004, 公路桥梁抗风设计规范[S].JTG/T D60-01—2004, Wind-resistant design specification for highway bridges[S].

[11] 刘凤华. 不同类型挡风墙对列车运行安全防护效果的影响[J]. 中南大学学报(自然科学版), 2006, 37(1): 176−182.LIU Fenghua. Wind-proof effect of different kinds of wind-break walls on the security of trains[J]. Journal of Central South University (Science and Technology), 2006,37(1): 176−182.