基于Copula模型变点检测的投资者情绪传染分析
2018-04-26凌志明王景乐
凌志明,王景乐
(对外经济贸易大学 统计学院,北京 100029)
0 引言
作为投资心理的投资者情绪正被越来越多的学者所关注。投资者情绪的定义主要从主观预期(偏好)与客观投资环境的偏差而产生,是对投资认知行为的一种反应过程。本文将投资者情绪定义为:投资者在投资过程中由于对外界客观环境与自身主观风险偏好的偏差,在投资过程中不断认知进而不断产生对当下或者未来投资环境及投资意向的一种判断,并影响投资行为。中外学者对投资者情绪的研究,主要集中在投资者情绪与证券收益的关系及投资者情绪与投资行为的研究。而对于投资者情绪的传染分析研究较少[1-4]。本文利用2010年后的数据,对中美两国投资者情绪的传染进行研究。由于目前的投资者情绪指标频度最多到周,月度数据比较普遍,因此本文设计的日度投资者情绪会更加精准地刻画投资者情绪的每日变化。本文利用变点检测方法结合Copula尾部相依系数,考察投资者情绪传染有无发生,并给出传染时间、大小及次数。同时运用非参数方法选择Copula模型,使模型的选择更加稳健。
1 模型与方法
1.1 Copula函数及其选择
Copula模型种类繁多。本文采用李霞(2014)[5]所介绍的非参数解析法选择Copula的模型。以常用单参数二元阿基米德Copula为例进行具体说明,其分布函数可由其组成的生成元表示:

其中,K(t)是C(u,v)的分布函数,是C(u,v)的生成元。阿基米德Copula函数作为备选模型进行具体的介绍:
(1)首先由原始数据产生相应的经验分布函数,通过散点图特征判断变量间的大致相依关系,以选出几个待评估的模型。
(2)设 (x1,y1),…,(xn,yn)是总体 (X,Y)中的一组样本,总体的联合分布函数记为H(x,y),对应的Copula为C(u,v),(x,y)的样本Kendall’sτ秩的相关系数表示如下:

同时,赵丽琴等(2009)[6]表示总体Kendall’sτ秩相关系数可由生成元φ(t)表示成从而总体秩相关系数可由样本秩相关系数来估计,也就是^τ=τ,由此可以计算出Copula函数中的参数。
1.2 变点检测方法
本文基于阿基米德Copula中的参数进行变点检测,参数可通过样本Kendall’sτ秩相关系数与生成元之间的关系估计。本文依据叶五一等(2009)[7]介绍的方法进行变点检测。
设θ是Copula函数的参数,假定θ只存在一个变点,可以建立相关原假设H0及备择假设H1:

其中,k*为变点时刻。
构造如下对数似然比检验统计量:
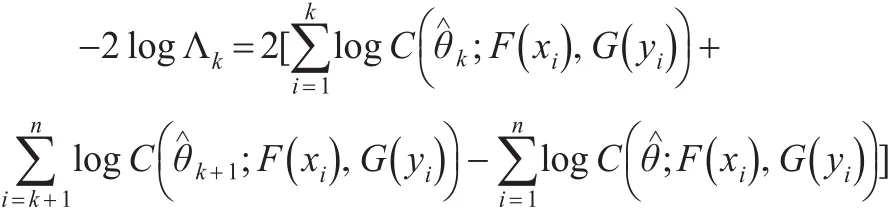
其中,是利用整体观测数据估计的参数,、分别为变点前或后的观测数据估计的参数,F(x)、F(y)是(x,y)的边缘分布函数。对于每一点k有1≤k≤n,利用如下检验量检验k是否为变点:

当该检验量很大时就可以拒绝原假设,即该Copula模型存在变点。Dias等(2002)[8]给出了上述检验问题的拒绝域的临界值。若只存在一个变点,变点k*的估计为:
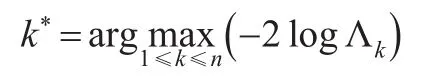
当存在多个变点时,本文拟采用Vostrikova(1981)[9]介绍的利用二分序列数据的方法进行多变点的检测。首先,检测出第一个变点,将数据在变点时刻分为两段序列,数据量分别为n1、n2,然后分别对这两组数据进行之前的单变点检测分析。如某段数据存在变点则继续将相应数据段在其变点时刻分为两段,继续对这两段数据进行单变点检测,直到数据段不能检测出变点为止。
1.3 投资者情绪传染检验及传染大小的度量
变点检测方法给出了两变量结构发生改变的时刻,但是对于投资者情绪传染的研究,仅检测变点并不能说明有传染以及传染的大小,本文用Copula尾部相依系数刻画变量之间的相依关系。尾部相依系数的定义如下:
设X,Y是边缘分布分别为F(x),G(y)的两个随机变量,其联合分布函数为C(u,v),上下尾部相依系数分别定义为λU、λL,且λU,λL∈[0 ,1],具体公式表示如下:

本文将变点前后相依系数的变化作为传染大小的度量,用 Δ 表示,令(或者其中λ0、λ1分别表示变点前后的尾部相依系数大小。具体解释为:如果变点前后尾部相依系数明显变化,若Δ>0,则两者之间存在传染,且传染增强;若Δ<0则两者虽存在传染,但是传染减弱。如果在变点时刻的前后尾部相依系数没有明显变化,则两者之间不存在传染。
2 实证分析
2.1 投资者情绪指标构建及分析
本文根据研究主题、指标频度、可供对比及数据来源等标准设计如下几个投资者情绪代理指标:
(1)中美证券市场指数点位(IP)。中美分别选取沪深300指数以及标普500指数。
(2)中美指数涨跌幅(CIP)。本文采用的是日数据,这里指数的涨跌幅是指当日收盘价与前一日收盘价的差额较前一日指数点的百分比。
(3)中美指数成交量涨跌幅(CITV)。
(4)中美基准利率变化幅度(CBIR)。基于投资者关注度、市场认可度以及数据来源角度,选取了上海同业拆借利率(Shibor)以及美国联邦基准利率。
(5)中美指数连涨连跌(SRF)的天数。记选取的样本数据段第一天该指标为1,日后若代表性指数涨则该指标在前一天基础上加1,若出现跌则减1,用整数的大小变化来描述市场涨跌变化。
(6)中美指数涨跌幅区间效应(PIE)。将指数涨跌幅处于上75%分位数和下25%分位数的数据分别记为暴涨、暴跌情况;刺激性涨跌幅度分别设置为上60%分位数至上75%分位数及下40%分位数到下25%分位数;而理性涨跌幅设置上60%至下40%分位数之间。本文将这五个区间依次称为暴跌恐慌、刺激性跌、理性涨跌、刺激性涨和暴涨恐慌,同时为处在这五个区间的涨跌幅所对应涨跌幅区间效应赋予数值,用(a,b,c,d,e)来表示,a—e分别为各自对应区间的平均值。
以上这些备选指标需要通过Baker等(2009)[3]的主成分方法进行筛选(本文称两阶段主成分方法)。具体步骤:将投资者情绪指标记为sent,对指标sent进行主成分分析,取贡献率达到85%以上的主成分构造一阶段投资者情绪指标sent1。然后将得到的投资者情绪指标与各备选情绪代理变量进行相关性分析,选取相关性较高的几个代理变量进行二阶段主成分分析,从而得到二阶段投资者情绪指标sent2,作为最终所要使用的投资者情绪指标。
本文选取中美两国从2010年首个交易日至2016年1月13日止的所有交易日的相关数据,其中除去了由于交易日不同的样本,保证了数据交易日的对应,共计1370期,全部数据来源于Wind金融终端。中美两国上述六个代理指标的描述性统计分析及相关性分析见下页表1和表2。
从表1和表2可以看出,各情绪代理指标之间的关系有正有负。除因构造方式引起的IP与CIP和SRF之间相关系数较高之外,大多数情绪代理变量之间相关性较弱。总体上,这些备选的代理变量能独立有效地代理投资者情绪进行综合投资者情绪指标的构建。
基于金融数据的“领先-滞后”现象,本文参考Baker等(2009)[3]的做法再引入各指标的滞后一期进行一阶段主成分分析(中美前六主成分贡献率分别是86.22%和91.92%),经加权平均后合成为一阶段投资者情绪指标。各代理指标及其滞后项之间的相关性结果如下页表3所示。
中美两国代理指标及其滞后项存在一致的结果:
sent1与 IPt、SRFt、IPt-1、CIPt-1、SRFt-1以及 PIEt-1相关系数高,故选择这六项指标进行二阶段的主成分分析,其余备选代理指标及其滞后项被剔除,金融市场基准利率及其滞后项都未被入选,原因可能是其他代理变量解释力度已经足够。二阶段主成分分析,提取前三个主成分(贡献率中美分别为98.69%及99.21%)加权平均后的二阶段投资者情绪指标的表达式为:

表1 中国情绪代理指标描述性统计分析及相关性分析

表2 美国情绪代理指标描述性统计分析及相关性分析

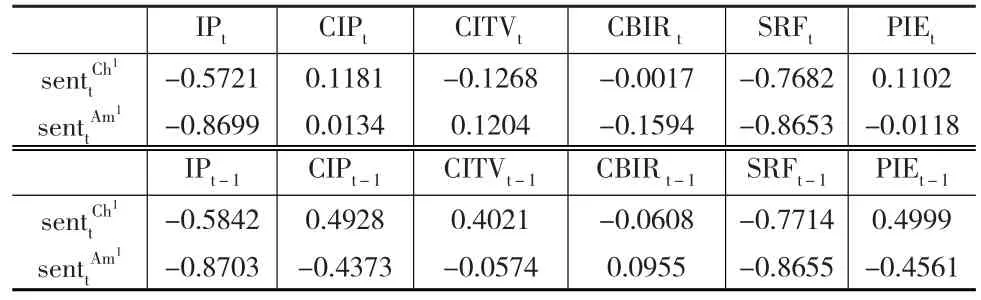
表3 一阶段投资者情绪指标与代理变量及其滞后项相关性
根据以上两阶段主成分分析后,得到最终所要研究的中美投资者情绪指标如图1所示(深色:中国)。从图1中可以看出中国投资者情绪趋势较复杂,具体来说,中国投资者情绪从样本数据段开始,经过一段时间上下波动后波动上升,然后骤降,后在2015年第二季度飙升后又骤降,之后又保持了上下波动状态,市场投资者情绪波动较大。美国投资者情绪指标近几年来大致呈现一种波动上升的趋势,特别是2010年到2012年末,波动幅度前期较后期大,2013年开始稳步上升后在2015年第二季度开始出现震荡下行态势。综合来看,两个市场在2014年上半年之前趋势较为一致,2014年下半年开始,两市场投资者情绪发展出现分歧,投资者情绪发展相对背离。
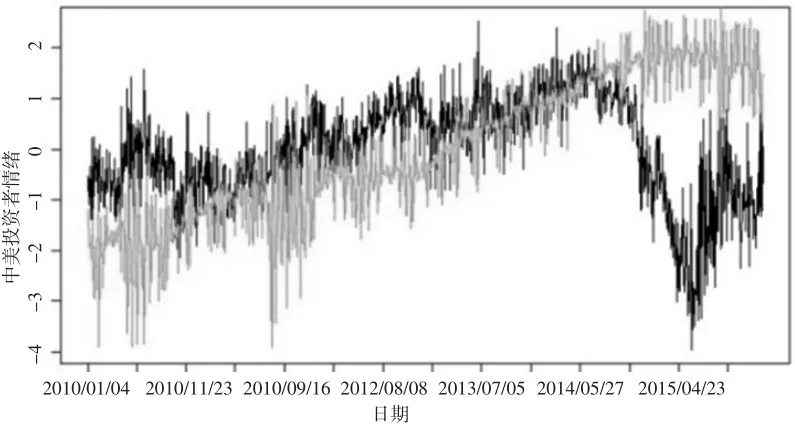
图1 中美投资者情绪指标
2.2 传染路径判别
对于传染路径的判断,本文采用格兰杰因果检验的方法。假设两个不同的市场各自的投资者情绪指标分别表示为sentA,sentB。判别模型及原假设如下:

原假设:H0:δ1=…δn=0
对上述方程的格兰杰因果检验,拒绝原假设则说明:sentB是引起sentA变动的格兰杰原因。类似地,可以检验sentA是否是sentB的格兰杰原因。
根据上文求得的中美投资者情绪指标,将中美两个市场投资者情绪指标记为sentCh及sentAm。格兰杰因果检验结果如表4所示。

表4 中美两个市场投资者情绪指标格兰杰因果检验
表4结果显示sentCh不是sentAm的格兰杰原因,而sentAm是sentCh的格兰杰原因,也就是说美国投资者情绪的变动引起了中国投资者情绪的变动,而中国投资者情绪的变动对美国投资者没有影响,只存在单向的关系。
2.3 Copula模型选择
基于上文的传染路径判别结果:中美两个市场之间的投资者情绪只存在美国市场对中国市场的单向传导基础上,本文进行下一步的Copula模型选择研究。选择具有尾部相依性的Gumbel Copula、Clayton Copula及Frank Copula作为备选Copula模型。

表5 三种备选Copula的估计参数
通过对比不同Copula所对应的t-K(t)与t-(t)图形,本文发现Clayton Copula是拟合最佳的Copula函数。同时,利用样本数据对这三个Copula函数进行拟合优度Kolmogorov-Smirnov检验,检验结果如表6所示,表中的K-S值表明Clayton Copula是最合适的Copula函数。

表6 备选copula函数拟合K-S值
2.4 变点检测及尾部相关系数
基于上文选择的最佳Clayton Copula函数为模型,进行变点检测,通过对投资者情绪指标计算后,得到了统计量ψn的值为717.0346,大于95%置信度时的临界值,得出第一个变点的时刻为2011年5月12日。将原始数据数据在2011年5月12日分为两段,两段数据量为对两部分数据分别进行变点检测,得到的统计量表示成ψn1和ψn2,统计量大小分别为70.1581和221.7392,后半段存在变点,变点时刻分别为2012年8月28日。继续对后半段在该变点时刻分为前后两部分,得到统计量值为56.7834和612.2582,同样后半段存在变点,变点时刻为2014年11月28日,并且继续检验该后半段的数据对应的统计量之后,他们的值都小于对应的临界值,几个变点检测相应数据段统计量-2logΛk图形如图2所示。因此本文认为已经不存在变点,故而进行接下来的尾部相关系数计算。

图2 变点前后数据统计量-2logΛk时间序列图
基于上文所计算出的三个变点,将原始数据在变点处分成前后两个部分,得到了三个前后区间的数据,分别是:(1)2010年1月4日到2011年5月12日,2011年5月13日到2016年1月16日;(2)2011年5月13日到2012年8月28日,2012年8月29日到2016年1月16日;(3)2012年8月29日到2014年11月28日,2014年11月29日到2016年1月16日。得到对应变点前后两部分的参数估计结果及对应的Clayton Copula下尾部相依系数,如表7所示。
最佳解释效果的Clayton Copula变点检测与尾部相关系数结果显示有三个变点,分别记为按照变点检测出现的顺序分别是:2011年5月12日、2012年8月28日、2014年11月28日。传染判别显示三个变点时刻都发生了传染,CP1及CP3对应的投资者情绪传染大小Δ为负数,说明这两个变点对应的前后两部分数据的传染大小减弱,而CP2对应的投资者情绪传染大小Δ是正数,传染大小增强。
第一个变点CP1(2011年5月12日)。中美投资者情绪相依系数从0.14下降到0.0286,降幅达到将近80%,可见美国投资者情绪在变点CP1之后对中国投资者情绪的影响呈现减弱态势。第三个变点CP3(2014年11月28日),中美投资者情绪相依系数从0.4553下降到0.0778,降幅达到将近82.47%,这一变点区间段前后数据传染性也减小。第二个变点CP2(2012年8月28日),中美投资者情绪相依系数从0.0638增加到0.1749,增幅达到174%,前后区段传染增强。

表7 变点前后Clayton Copula参数估计θ^及下尾部相依系数
3 结论
本文通过6个投资者情绪代理指标,考察了中美两国市场投资者情绪传染的途径,并分析了情绪传染的时间和强弱。得出如下结论:第一,存在美国投资者情绪对中国的单方面传染,而不存在中国对美国的传染;第二,在本文采用的样本区间内,共发生了3次情绪传染。通过传染前后的分析可以看出,随着中国市场的不断发展,中国投资者变得更加理性,美国投资者的情绪对中国的传染在进一步的减弱。
参考文献:
[1]Tay N S P.Social Network Characteristics and the Evolution of Inves⁃tor Sentiment[M].Japan:Springer,2009.
[2]Hudson Y,Green C J.Born in the USA?Contagious Investor Senti⁃ment and UK Equity Returns[J].Discussion Paper,2013.
[3]许祥云,廖佳,吴松洋.金融危机前后的中国股债关系分析——基于市场情绪变化的解释视角[J].经济评论,2014,(1).
[4]文凤华,杨鑫,龚旭等.金融危机背景下中美投资者情绪的传染性分析[J].系统工程理论与实践,2015,(3).
[5]李霞.Copula方法及其应用[M].北京:经济管理出版社,2014.
[6]赵丽琴,籍艳丽.Copula函数的非参数核密度估计[J].统计与决策,2009,(9).
[7]叶五一,缪柏其.基于Copula变点检测的美国次级债金融危机传染分析[J].中国管理科学,2009,(3).
[8]Dias A,Embrechts P.Change-Point Analysis for Dependence Struc⁃tures in Finance and Insurance[J].Social Science Electronic Publish⁃ing,2002.
[9]Vostrikova L Y,Vostrikova L Y.Detecting“Disorder”in Multidimen⁃sional Random Processes[J].Soviet MathmaticsDoklady,1981,24(1).
