引入地理回归加权的非参数平滑改进的非寿险广义线性模型

闫 春，董婷婷，邱艺伟，刘 倩

（山东科技大学 数学与系统科学学院，山东 青岛 266590）

0 引言

未决赔款准备金评估模型的平滑化研究始于上世纪70年代，早期指的是进展因子的平滑处理，后来由于随机模型框架的建立，又产生了模型参数的平滑与非参数平滑方法的研究。90年代，广义线性模型被引入到精算领域，在非寿险费率厘定与准备金估计方面都有广泛的应用。随着研究的不断深入，广义线性模型在其应用中也得到不断改进。

在准备金评估方法中的随机方法中，广义线性模型应用广泛，且相对能够较好的适用于实际的非寿险评估中。但广义线性模型存在着一些不足，在相当多的实际案例中，其参数模型并不能够充分的描述索赔数据。因此，本文将非参数引入广义线性模型，通过多种平滑方法，将事故年和进展年抽象为位置数据融入到广义线性可加模型中，是将非参数方法与准备金评估方法的一次结合，来实现对GLM准备金评估模型的非参数平滑改进。

1 广义线性模型介绍

广义线性模型（GAM）最早由Nelder和Wedderbum在1972年提出，是对线性回归模型的推广。GLM涵盖了一大类统计模型，不仅包括经典的线性回归模型和方差分析模型，还包括对数线性模型、泊松回归模型、Logistic和Probit模型及多分类反应变量模型等。广义线性模型可以有效处理各类离散型的观测数据，在生物医学、社会调查和工业产品质量评估领域都有广泛的应用。

1.1 广义线性模型理论

广义线性模型有三个组成部分：随机部分、系统部分和联结函数。

随机部分。属于指数分布族的相互独立的随机变量yi，密度函数为：

其中θi和φ为参数，b和c为函数。yi的期望为μi，方差为均值的函数，即有θb′(θi)。其中b′(θ)和b′(θ)分别表示函数b的一阶和二阶导数。

系统部分。假设x1，x2，…，xp为对应于y1，y2，…，yn的p维自变量的值，存在某线性预估量η，是参数β1，β2，…，βp的线性函数，有：

联结函数。联结函数是指观测值xi与指数散布族的期望μi之间的函数关系。随机部分和系统部分通过ηi=g(μi)连接在一起，g(·)称为联结函数。容易得到：

其中，β为未知实参数表示第i个观测向量。

1.2 常见的指数型分布

前面提到，广义线性模型的随机部分属于指数型分布。常见的指数型分布有正态分布N(μ，σ2)、二项分布B(1，p)、泊松分布P(λ)、伽玛分布 Γ（μ，γ）和逆高斯分布IG(μ，σ2)等。这些分布如表1所示。

表1 指数型分布的几个例子

1.3 准备金评估的广义线性模型

在准备金评估的广义线性模型中，观测值通常是已知的赔案数据，此时的赔案数据称为反应变量。反应变量不同，模型也不同，如对案均赔款、索赔次数分别建模的两阶段广义线性模型和对增量已决赔款、增量已报案赔款分别建模的随机性准备金进展模型。本文仅讨论对已决赔款建立的广义线性模型。

观测值Xi，j的分布可以由数据样本分析得出，也可以由精算人员假定。精算人员通常在不同分布假设下分别建立不同的模型，再其对样本的拟合效果结合实际进行选择。

联结函数一般采用对数联结，见England(2001)。此时未决赔款准备金广义线性模型为：

模型假设增量已决赔款Xi，j属于指数分布族，mij为Xi，j的均值，方差函数为散度参数。p=0，1， 2， 3 时Xi，j分别对应为正态分布、Poisson分布、Gamma分布和逆高斯分布。

在准备金评估的广义线性模型中，考虑不同的影响因素，线性估计量ηij也不同，主要有：

在模型求解时，不妨建立约束条件α1=β1=γ2=0，以保证参数估计的唯一性。在余下的模型参数中需要估计的变量数为3t-2个。由统计软件得到各参数的估计值计算得到m̂ij，则可求得准备金的估计值。随机部分是根据线性估计量选定的设计矩阵。

2 非参数平滑改进广义线性模型

2.1 广义可加模型

在相当多的实际案例中，参数模型并不能够充分的描述索赔数据，因此非参数模型就被应用到了索赔数据的评估中。通常将这种在传统广义线性模型中引入非参数部分的模型叫做广义可加模型（GAM）。

这种非参数模型与广义线性模型有着密切的联系，但GAM改变了传统GLM的线性预估量。对于模型（5）和（7），即不考虑通胀因素，GAM的预估量可以写为：

其中sθi(i)是与事故年有关的连续变量，sθj(j)是与进展年有关的连续变量，θ是由精算人员确定的平滑因子。

GAM的预估量可以通过局部加权回归平滑(LOESS)、平滑样条函数或者核光滑来创建。三次平滑样条可以通过最小化惩罚残差的平方和来得到：

在该模型中，平滑参数θ取值越大，模型的方差就越小，但偏差会增加。若θ接近于零，函数完全拟合每个点，模型更像链梯估计。若θ接近无穷大，模型趋于线性，因此更像GLM。

sθ的LOESS估计能够通过以下算法计算：

（1）定义N(x0)为区间(x0-k，x0+k)上数据的集合。

（3）对N(x0)中的每个点计算权重wi，有：

其中T为三次权函数：

（4）用权重{w1，w2，…，wm}作Y对N(x0)中X的回归。

当误差服从非正态分布并且来自于一个指数类，可以适用上述带加权的公式。此外，GAM要求各列损失的和大于或等于零，如果不能满足，可以添加常数项进行适当调整。

模型的预估量由一个参数组合和一个非参数的函数组成：

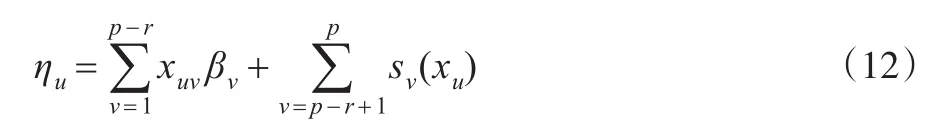
其中，p为预估量的个数，r为预估量参数的个数。

2.2 GWR理论与位置加权广义线性模型

在对有关位置的数据进行分析时，传统的线性回归模型是全局的空间回归模型，通常假定模型参数与样本数据的位置无关，那么得到的回归参数β̂MLE既是该点的最优估计，也是整个研究区域内所有点的最优估计。然而在实际问题中，回归参数在不同位置上往往表现不同，回归参数估计值就不能反映回归参数的真实空间特征，也不能精确地探测研究对象在空间上的非平稳性。

为了解决这一问题，Foster&Gorr（1986）提出了空间变参数回归模型，将数据的空间结构嵌入到回归模型中，使回归参数变成有关观测点地理位置的函数。Fortheringham等（1997）在此基础上利用局部光滑的思想，提出了地理加权回归模型（GWR）。对于全局的普通线性回归模型：

GWR扩展了传统的回归框架，引入了能够估计每个样本数据空间位置的参数值。有：

其中（ui，vi）表示位置i的坐标。

这样可以定义位置加权广义线性回归模型。设y1，y2，…，yn为因变量的n个独立观测，概率密度函数为：

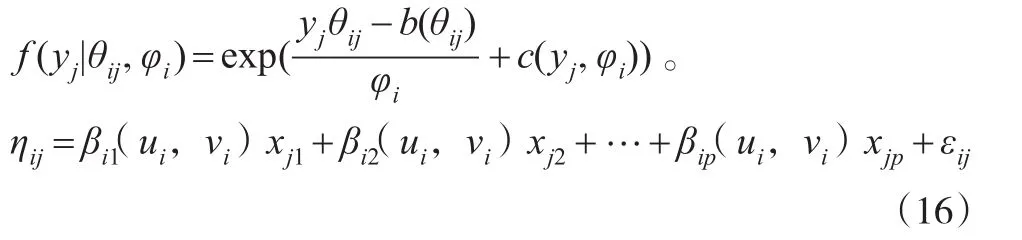
这样，β（kui，vi）就是连续函数β（ku，v）在点i的值，从而参数值β（ku，v）表现为一个连续的空间平面。

2.3 GLM非参数平滑改进模型

由GWR理论的思想，结合应用非参数广义线性模型评估准备金的方法，对于模型（5）和模型（6）都可以由式（17）来假定评估模型的线性预估量。

对于最简单的模型（5），引入位置参数(u，v)，有：

对模型（6），有：

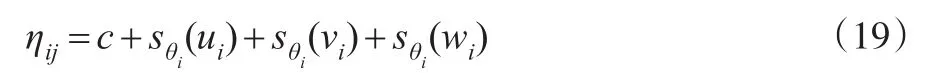
其中，wi为对角线参数。

由于位置加权广义线性回归模型中的回归参数在每个数据采样点上都不同，因此其未知参数为n×(p+1)个，远远大于观测个数n，这样就不能直接利用参数回归估计其中的未知参数。Brunsdon等（1996）采用了一类非参数光滑方法为该模型的拟合提供了一个可行的思路，即在局部多项式光滑的思想上提出了偏差和方差折衷的解题思路。假设回归参数为一连续平面，以采样点i和其邻域采样点上的观测值构成局域子样，建立全局的线性回归模型，然后采用最小二乘方法得到回归参数估计。对于其它采样点，采用另一个相应的局域子样来估计，以此类推。

为了充分利用己有观测值并减少子样规模扩大引起的偏差增加，后来Brunsdon又对这种方法进行了修正。在估算采样点i的回归参数时，距离点i越近的观测值重要性越大，越远的观测值重要性越小，根据加权最小二乘方法（WLS），得到i点的回归参数βi1，βi2，…，βip。根据上述思想，则第i点的回归参数的估计方程为：

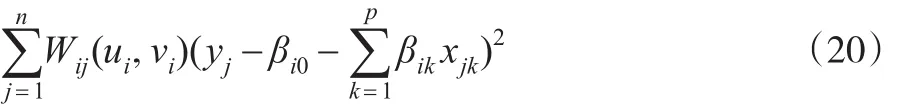
其中Wij(ui，vi)为位置 (ui，vi)的权重。解上述方程，矩阵形式表示的解为：

按上述方法逐点进行回归计算，得到所有点的回归参数的估计值，不同采样点上的估计值反映了对应的变量间的关系在研究区域内的变化情况。

3 实证分析

本文用来实证分析的赔款额增量数据见表2，最早出现于Taylor和Ashe（1983）中。

采用表2中算例，使用R软件中Chain Ladder包中的glmReserve()函数，对模型（5）可以得到本文数据样本下GLM的相关估计结果，见表3。此时假设反应变量为过度分散泊松分布。表4为各参数估计表。

表2 赔款额增量流量三角形

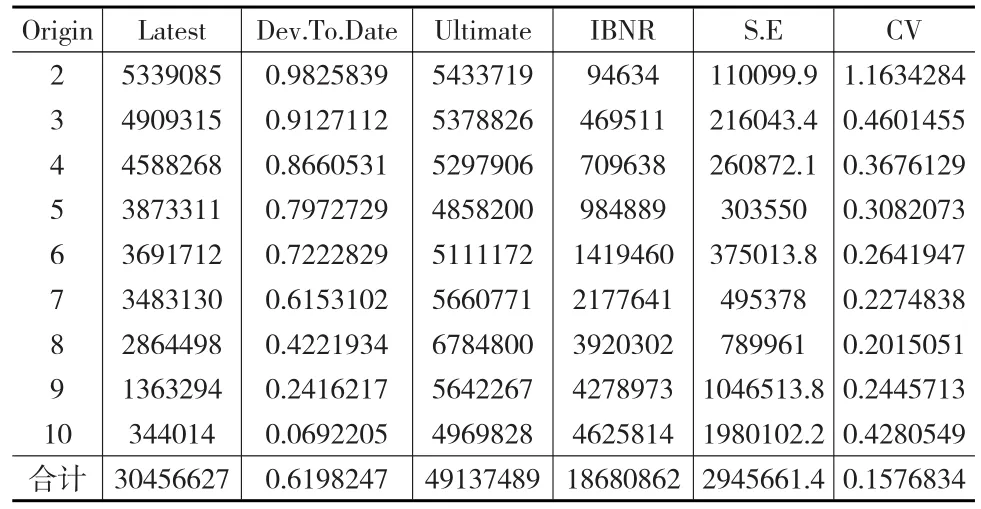
表3 过度分散泊松分布GLM的计算结果

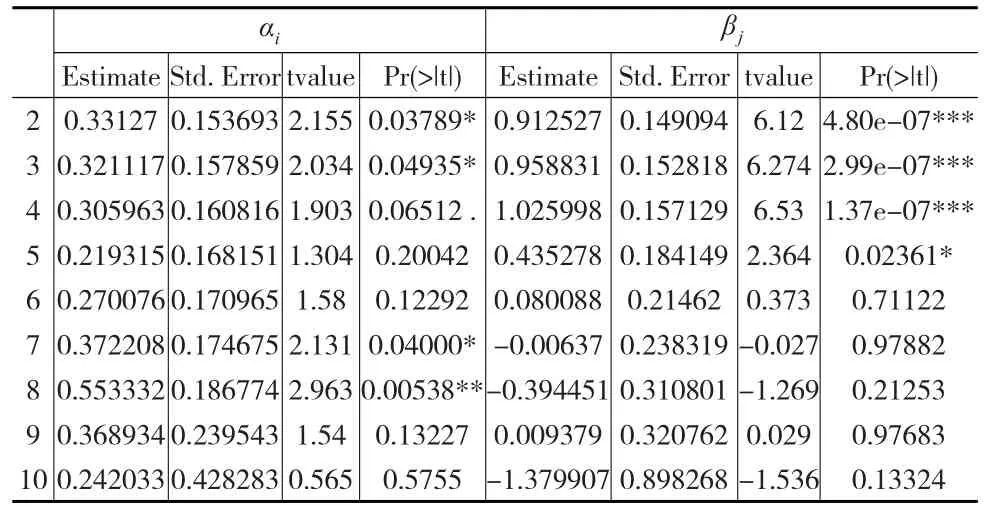
表4 参数估计表

表4显示，从第6个进展年开始，有Pr(＞|t|)＞0.1。分别考虑从第6个进展年参数开始平滑与仅平滑最后三个进展年，取本年及其前1、2个进展年参数的权重分别为、和，递归计算，得到的IBNR评估对比结果如表5

所示。

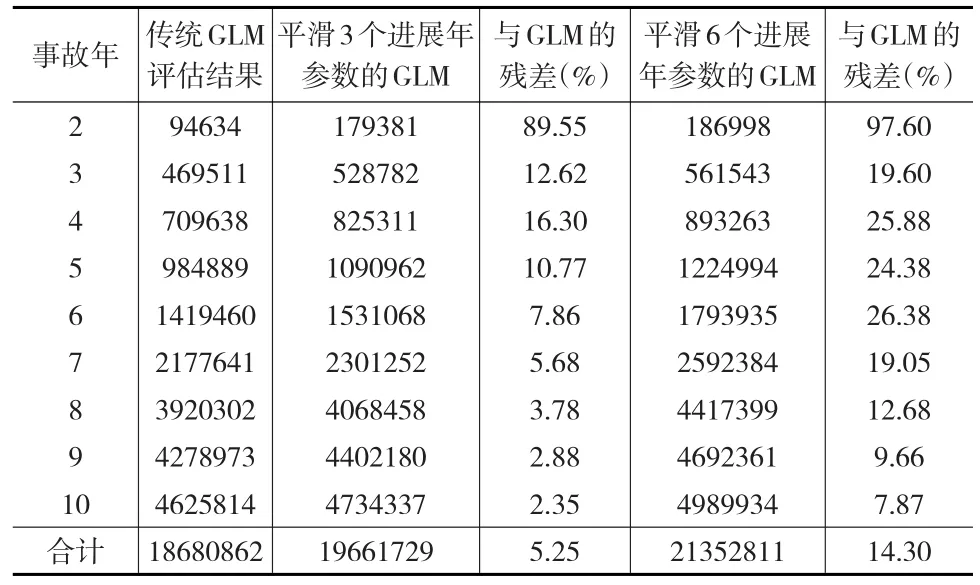
表5 IBNR评估结果对比表

可见，平滑3个进展年参数的IBNR评估结果每一年都比传统的广义线性模型评估结果多，总准备金比其多5.25%。而平滑6个进展年参数的GLM评估结果要比传统模型多14.3%，这都在可以接受的误差范围之内。且后者每一事故年的IBNR评估结果都比前者多。因此要灵活选取需要平滑的参数。

分别把(1,8)、(5,4)、(7,2)位置的已决赔款扩大10倍，以此来分析有异常值存在的情况，评估结果见表6。

表6 准备金评估结果对比表

通过分析引入异常点与引入前的准备金评估结果残差，可知该方法对实现尾部数据的平滑有一定的效果。

引入位置参数(u，v)，做位置加权的GAM平滑，事故年和进展年分别产生的影响如图1所示。

图1 事故年和进展年因素拟合情况

参数u的p值为0.11，v的p值为2.45e-15，可见进展年的影响已经非常显著。其中，位置加权的GAM增量赔款下三角估计值见表7。

可以得到，总准备金估计值为18417168。对100个增量赔款数据绘制散点图可以清晰地看到拟合以及预测情况。图2中的误差范围显示，模型能较好地平滑评估结果。

表7 增量赔款额下三角估计值

图2 事故年和进展年因素总拟合情况

4 结论

在准备金评估方法中的随机方法中，广义线性模型应用广泛，且相对能够较好地适用于实际的非寿险评估中。但广义线性模型存在着一些不足，在相当多的实际案例中，其参数模型并不能够充分的描述索赔数据。因此，本文将广义线性模型和地理回归加权模型结合，在广义线性模型引入非参数，通过多种平滑方法，将事故年和进展年抽象为位置数据融入到广义线性可加模型中，来实现对GLM准备金评估模型的非参数平滑改进，并利用R软件对其平滑性作出了实证。通过实证结果可以看出，本文引入地理回归加权的非参数平滑改进广义线性模型能够较好地平滑评估结果，且对实现尾部数据的平滑也有一定的效果。

参考文献：

[1]Foster A S，Gorr W L.An Adaptive Filter for Estimating Spatially Varying Parameters:Application to Modeling Police Hours Spent In Response to Calls for Service[J].Management Science,1986,32(7).

[2]Fotheringham A S.Trends in Quantitative Methods I:Stressing the Lo⁃cal[J].Progress in Human Geographically,1997,21(1).

[3]Brunsdon C,Fotheringham A S,Charlton M.Geographically Weight⁃ed Regression:A Method for Exploring Spatial Nonstationarity[J].Geo⁃graphical Analysis,1996,28(4).

[4]Bjorkwall S,Hossjer O,Ohlsson E.Non-parametric and Parametric Bootstrap Techniques for Age-to-Age Development Factor Methods in Stochastic Claims Reserving[J].Scandinavian Actuarial Journal,2009,(4).

[5]Bjorkwall S,Hossjer O,Verrall R J.A Generalized Linear Model With Smoothing Effects for Claims[J].Insurance:Mathematics and Economics,2011,49(1).

[6]彭景云.评估IBNR准备金的随机方法[D].上海：华东师范大学硕士学位论文,2007.

[7]韦冬艺.基于平滑效应的未决赔款准备金广义线性模型[D].天津：天津财经大学硕士学位论文,2012.

[8]宋昕.个体数据模型准备金评估:带有插补值的多元核密度估计方法[D].上海：华东师范大学硕士学位论文,2013.

[9]段白鸽,张连增.索赔准备金评估的贝叶斯非线性分层模型[J].山西财经大学学报,2013,(10).

[10]闫春,张良玉.非寿险未决赔款准备金评估的广义线性模型平滑性改进[J].系统工程,2014,(1).