EMA行星架多目标优化与疲劳可靠性分析*

呼斯乐图，段富海，，※，来进勇，安 玮

0 引言

随着多电/全电飞机的迅速发展，襟翼机电作动器（Electro-Mechanical Actuator，EMA）因具有体积小、重量轻、可靠性高等特点，逐渐替代传统飞机上的液压作动器，成为国内外先进飞机襟翼的驱动装置[1]。EMA减速器组件各传动部件在飞机起飞着陆时承受随机交变载荷，薄弱部位容易变形或产生裂纹，甚至发生失效破坏，从而严重影响齿轮啮合，进而产生较大的输出扭矩误差。行星架是行星减速器的关键承力件，它承受齿轮啮合力、离心力、重力等静态载荷，同时承受发动机以及飞机起飞着陆滑行时产生的振动载荷。因此，为提高行星架的承载性能，必须对其进行静动态分析、结构优化以及疲劳可靠性分析。

现代计算机仿真技术的快速成熟，采用CAD/CAE联合仿真分析与多目标优化设计受到众多企业的青睐[2]。在结构性能目标要求较多时，多目标优化设计为最有效的解决方法。遗传算法由于响应速度快、全局搜索能力强，是广泛采用的一种现代智能多目标优化算法，它在一次运行中就可以得到Pareto解集，避免了传统优化算法的多次运行问题[3-4]。

本文对襟翼EMA齿轮减速器行星架进行静动态分析、多目标优化设计与疲劳可靠性分析。针对行星架多目标要求，采用基于响应面的多目标遗传算法进行优化设计与求解。通过试验设计（Design of Experiment，DOE）、建立响应面模型和灵敏度分析，得到最佳设计点与目标参数，最后通过对优化后的行星架进行疲劳可靠性分析，全面评估了其静动态性能、安全性与可靠性。

1 行星齿轮差动减速器系统分析

1.1 结构与工作原理

EMA行星齿轮差动减速器是飞机襟翼装置的关键组件，主要由太阳轮、行星架、行星轮、套筒、输出齿轮轴等组成，结构组成与工作原理如图1所示。

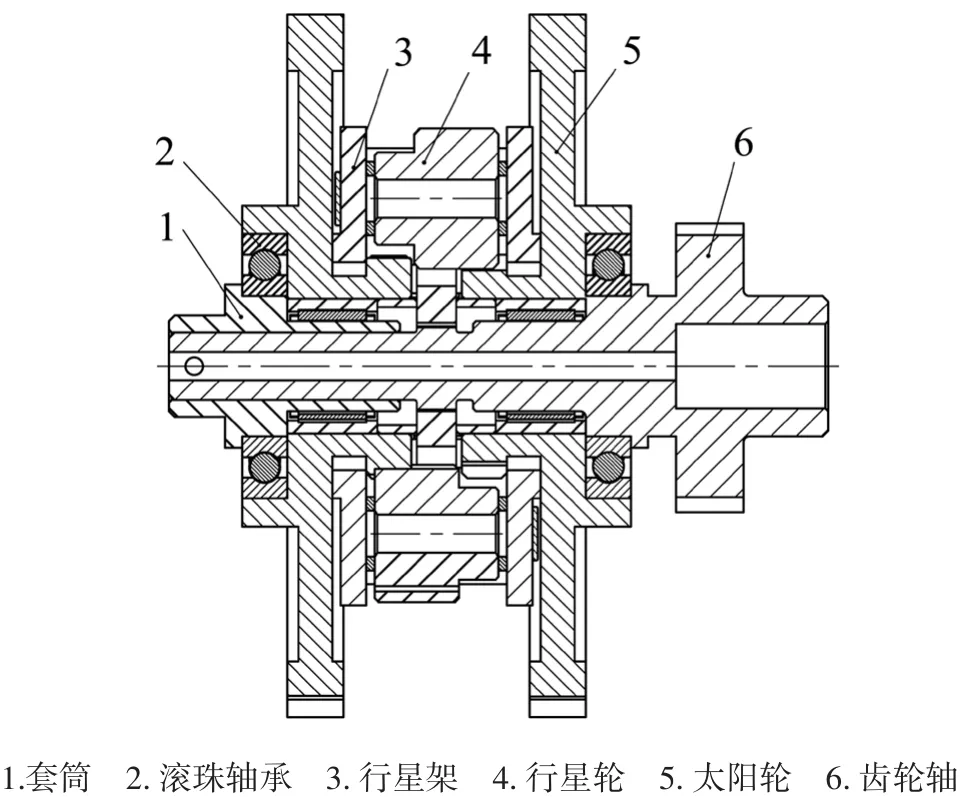
图1 行星齿轮差动减速器结构图Fig.1 Structural diagramof planetary gear differential reducer

减速器内部传动主要由行星齿轮传动和差动齿轮传动两部分组成。工作时两个电机分别在两个大齿轮（太阳轮）啮合，两个大齿轮内部的齿与三对相啮合的行星齿轮啮合，相啮合的行星轮相互作用使行星架转动，带动其相啮合的输出齿轮轴转动[5]，从而带动飞机襟翼伸出或收回。

1.2 行星架受力分析与计算

当减速器工作时行星架左右两侧板支撑行星轴与行星轮并使行星轮之间有效啮合，同时中心内齿与输出齿轮轴相啮合，故其承受的工作载荷主要由三部分组成：

（1）行星架与输出齿轮轴的啮合力F1；

（2）行星架转动过程中由行星齿轮与轮轴给它的离心力F2；

（3）行星架自身的重力，以重力加速度g=9.806 65 m/s2的形式来确定。

1.2.1 计算啮合力F1

一般两个齿啮合传动时，在忽略齿间摩擦情况下，会受到法向压力，以Fn表示，又称名义载荷。Fn可分解为与节圆相切的圆周力Ft和指向轮心的径向力Fr两个相互垂直的分力，三者关系如下：

式（1）中，T为齿轮轴给支架的扭矩（N⋅m）；d=17 mm为分度圆直径；θ=20∘为压力角。

减速器最末端输出轴的额定负载扭矩Tload=120 N·m，经传动比与传动效率计算得到齿轮轴上的最大扭矩T=36.5 N·m。再由式（1）计算得 Ft=4 294 N 、 Fr=1 563.89 N 、Fn=4 569.58 N，即啮合力：

F1=Fn=4 569.58 N

1.2.2 计算离心力F2

行星架转动时承受行星轮与行星轴传来的离心力，即向心力。当转速较高时对行星架的性能影响较显著，由下式求得：

式（2）中，m为一个行星轮与行星轴质量之和，（kg）；υ为行星架最高圆周速度，（m/s）；r为行星轴孔中心到行星架中心距离，（m）；ω为行星架最高角速度，（rad/s）。

对研究的EMA， m=0.5 kg， r=0.03 m，ω=260rad/s；代入式（2）得出F2=1 014 N。

2 行星架静动态特性分析

2.1 应力和变形分析

根据行星架受力计算结果进行静动态分析，内容包括行星架参数化建模、网格划分、材料属性设置、边界条件设定和分析求解。行星架是整个减速器主要承力件，材料30CrMnSiA是具有高韧度、疲劳性能较好的合金结构钢，主要属性为：弹性模量1.96×105MPa、密度7 750 kg/m3、泊松比0.3。网格划分是建立有限元模型的关键环节，本文综合考虑网格数量、疏密、质量等，采用自动划分与局部细化相结合的方式。由于重点关注行星架与齿轮轴啮合以及行星轮轴支撑孔的受力状态，故在此处网格较细密，而支架其他部分网格相对稀疏，以节省计算机内存与提高计算效率。经划分产生386 689个节点，253 452个单元，图2（a）为有限元模型。根据减速器的结构特点、工作原理以及受力计算结果对行星架设定边界条件（约束与载荷），分析计算得到图2（b）和（c）结果分布云图。

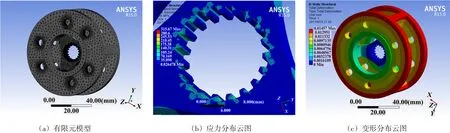
图2 行星架有限元模型与分析结果分布云图Fig.2 Finiteelement model and analysisresultsnephogramof planetary carrier

由图2（b）和（c）可见，等效应力值为315.67 MPa，材料屈服强度为850 MPa，故安全系数较高；变形量为0.014 57 mm，远小于行星架许用最小变形量0.2 mm。强度和刚度均满足使用要求并有较大的优化空间。

2.2 振动模态分析

模态分析属于结构固有特性分析。一般情况下低阶固有频率和振型对结构的影响较大（频率从低阶往高阶逐渐增大）。因此本文只提取模态1阶固有频率和对应的振型，如图3所示。

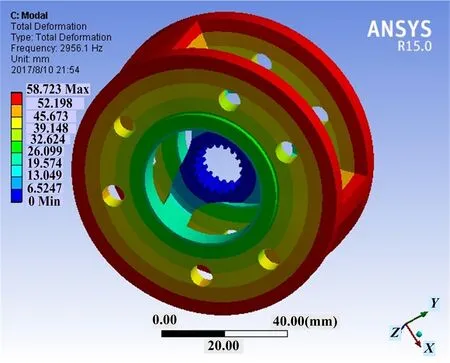
图3 模态分析1阶振型Fig.3 The1 stagevibration modeof modal analysis

由分析结果知，行星架1阶固有频率为2 956.1 Hz。由相关资料得知，由于襟翼离发动机较近，因此它的工作频率较大，一般为350～2 060 Hz。容易看出，一阶固有频率与最大工作频率具有一样的数量级，当减速器由于工作突发情况频率增大时可能与行星架结构的某一固有频率比较接近或相吻合，这就会使结构系统产生较大的振动或共振，并导致在行星架某些部位产生数值很大的振动响应，严重影响襟翼操纵性能。故需对它进行优化分析，提高固有频率。

3 行星架多目标优化设计

3.1 建立数学模型

多目标遗传算法可快速准确求解多约束多目标的非线性问题，并具有全局搜索能力。在多目标优化问题中得到的不是一组解，而往往是一系列解，即帕累托（Pareto）解集[6-7]。与多目标优化问题描述相结合建立行星架数学模型，以连接板、侧板和中心板厚度为设计变量；以最大等效应力与最大变形量为状态函数，即约束条件；以质量、一阶固有频率作为目标函数，建立优化数学模型为：

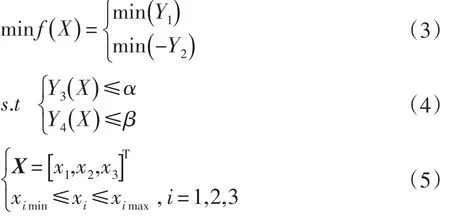
式（3）-（5）中， f(X)为目标函数；Y1为质量；Y2为一阶固有频率；Y3为整体变形量；Y4为最大等效应力；α为最小变形量；β为等效应力边界值；X为设计变量向量，x1为连接板厚度，x2为侧板厚度，x2为中心板厚度；ximin、ximax分别表示设计变量最小值与最大值。

3.2 试验设计（DOE）

试验设计是多目标优化设计的关键环节，是根据设计变量与状态变量取值范围来生成一系列设计点的过程[8]。因此，首先确定其边界条件，一般设计变量的变化范围（上下线）设置为≤±10%。三个设计参数变化范围分别设置为x1～DS_ljbHD 为 6.3～7.35mm、 x2～DS_cbHD 为 5.4～6.3 mm、 x3～DS_zxbHD为8.1～9.45 mm；状态变量边界值取α=0.02 mm， β=380MPa。设置完进行DOE求解，得出15组初始试验设计点、目标参数值与它们之间的关系曲线。表1为试验设计点与参数值。

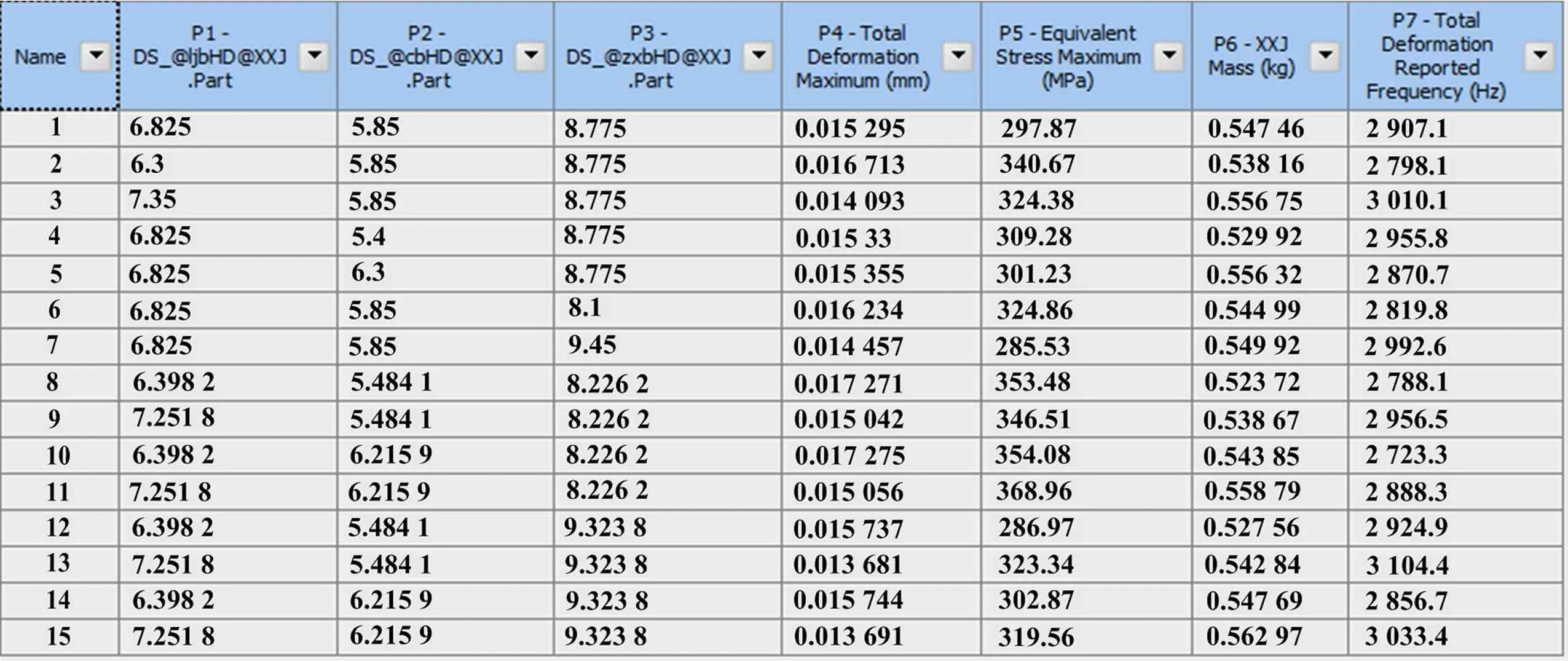
表1 试验设计点与参数值Tab.1 Experimental design point and parameter value

通过以上15组初始试验设计点，拟合出设计点与目标参数1阶固有频率、质量的关联图，如图4所示。

3.3 响应面优化设计

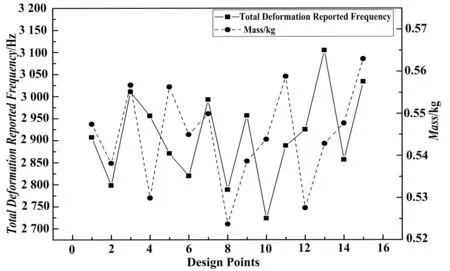
图4 设计点与目标参数关系曲线Fig.4 Relation curve between design points and target parameters

响应曲面优化可直观地观察到各输入参数对优化目标的影响，能够动态表征输入输出参数的关系[9-10]。对以上得出的设计点，采用完全二次多项式对样本点进行响应面拟合，得到图5所示设计变量对目标参数的响应趋势的三维图。

3.4 优化结果分析

通过对响应曲面进行计算处理，得到图6所示三组优化结果。

由以上三组候选结果折中确定最优解为Candidate Point2，因此得到各参数的最优值分别为：DS_ljbHD=6.5 mm、DS_cbHD=5.4 mm、DS_zxbHD=9.4 mm、一阶固有频率为2 979.2 Hz、质量为0.526 4 kg。为更直观显示与优化前的性能对比关系，表2列出优化前后的各性能参数。

由表2对比可见，最大等效应力减小显著，比优化前减小10.36%；最大变形量比优化前略有增加，变形量为0.015 2 mm，但在材料刚度允许范围内；质量减少5.54%，固有频率增加0.78%，达到预定目标要求。

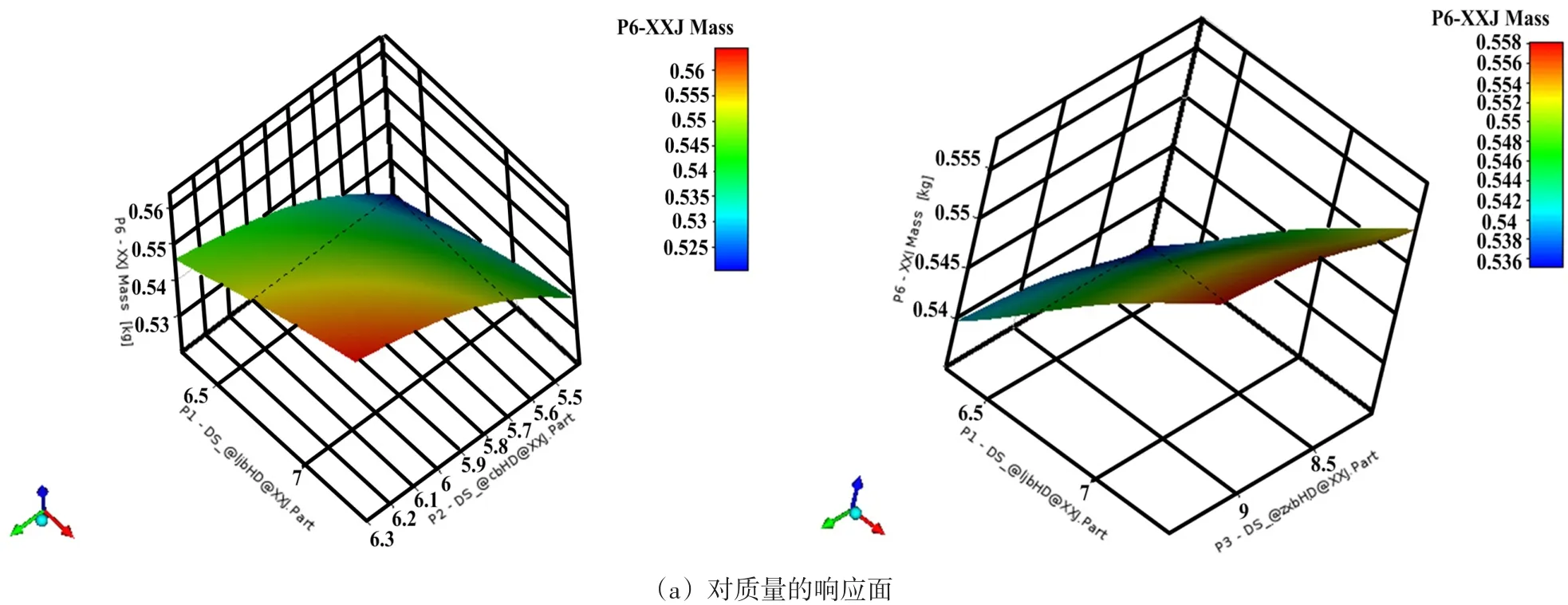
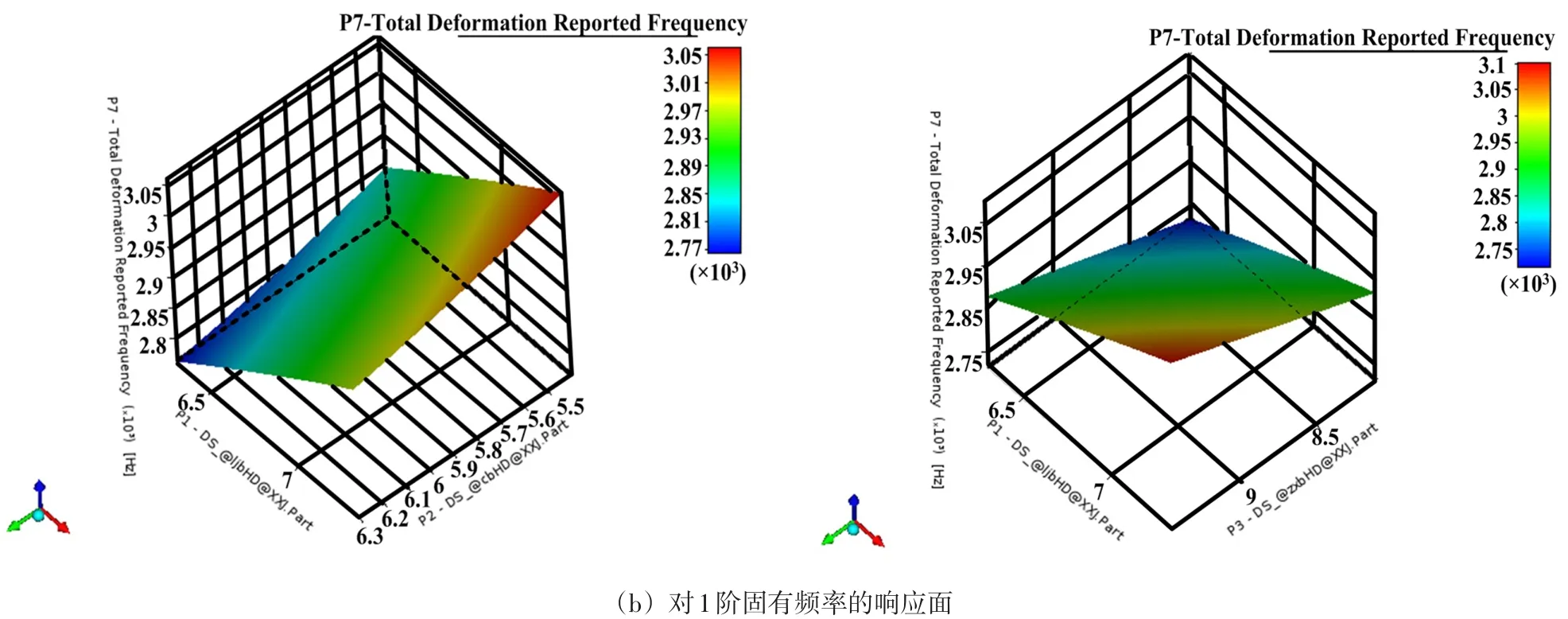
图5 设计变量对目标参数的响应面Fig.5 Responsesurfaceof design variablestotarget parameters

图6 优化结果Fig.6 Optimization result

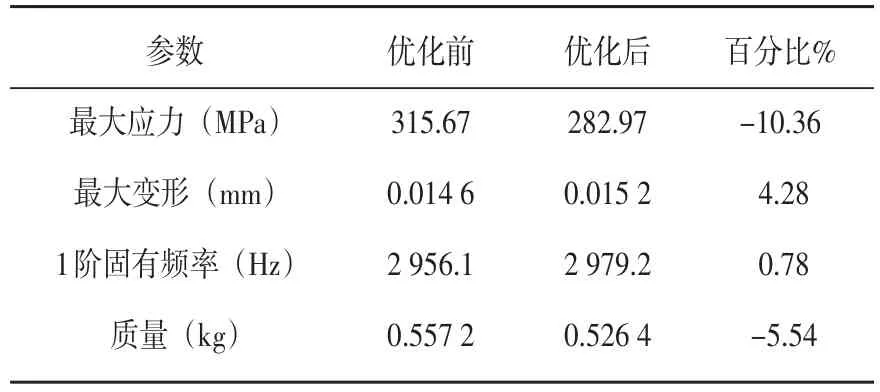
表2 优化前后参数对比Tab.2 Comparison of parameters beforeand after optimization

3.5 灵敏度分析

考虑各设计参数对目标函数的影响程度并为后续可靠性分析提供支撑，进一步对设计参数进行灵敏度分析。灵敏度分析是分析设计变量（输入参数）对状态参数与目标参数的影响程度。图7为参数灵敏度分析图。

由图7可见，ljbHD与zxbHD对状态和目标参数的影响程度比较明显，其中ljbHD对最大变形量、1阶固有频率及质量的影响较大；cbHD对所有参数的影响微小。说明连接板厚度与中心板厚度的变化对行星架静动态性能影响显著，这也会对其疲劳耐久性与可靠性产生一定的影响。

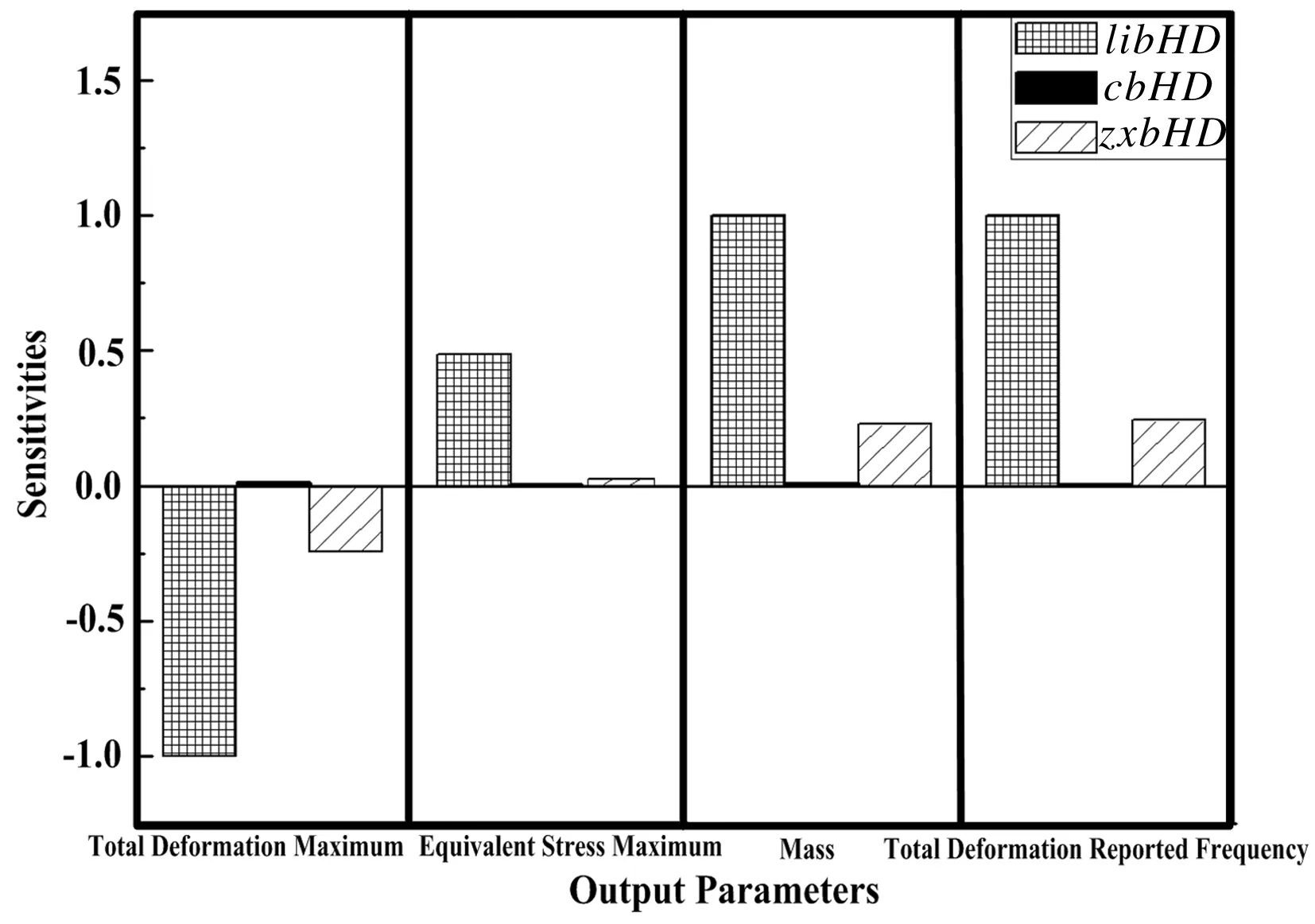
图7 参数灵敏度分析图Fig.7 Parametric sensitivity analysisdiagram

4 疲劳可靠性分析

为进一步保证优化后行星架的安全性、耐久性与可靠性，对其进行疲劳可靠性分析。疲劳可靠性分析主要研究部件在随机载荷作用下的疲劳寿命与可靠性[11-12]。6sigma可靠性分析是一种基于概率统计的计算输出参数概率分布的方法，表示100万件产品中只有3.4件不合格品的概率[13-14]。

4.1 疲劳寿命分析

行星架工作中受到各种交变的随机载荷，影响行星架寿命。结合实际工作环境与实测数据，确定随机载荷谱。边界条件的设定与静态分析时一致，经分析得出图8所示安全系数与疲劳寿命分布云图。

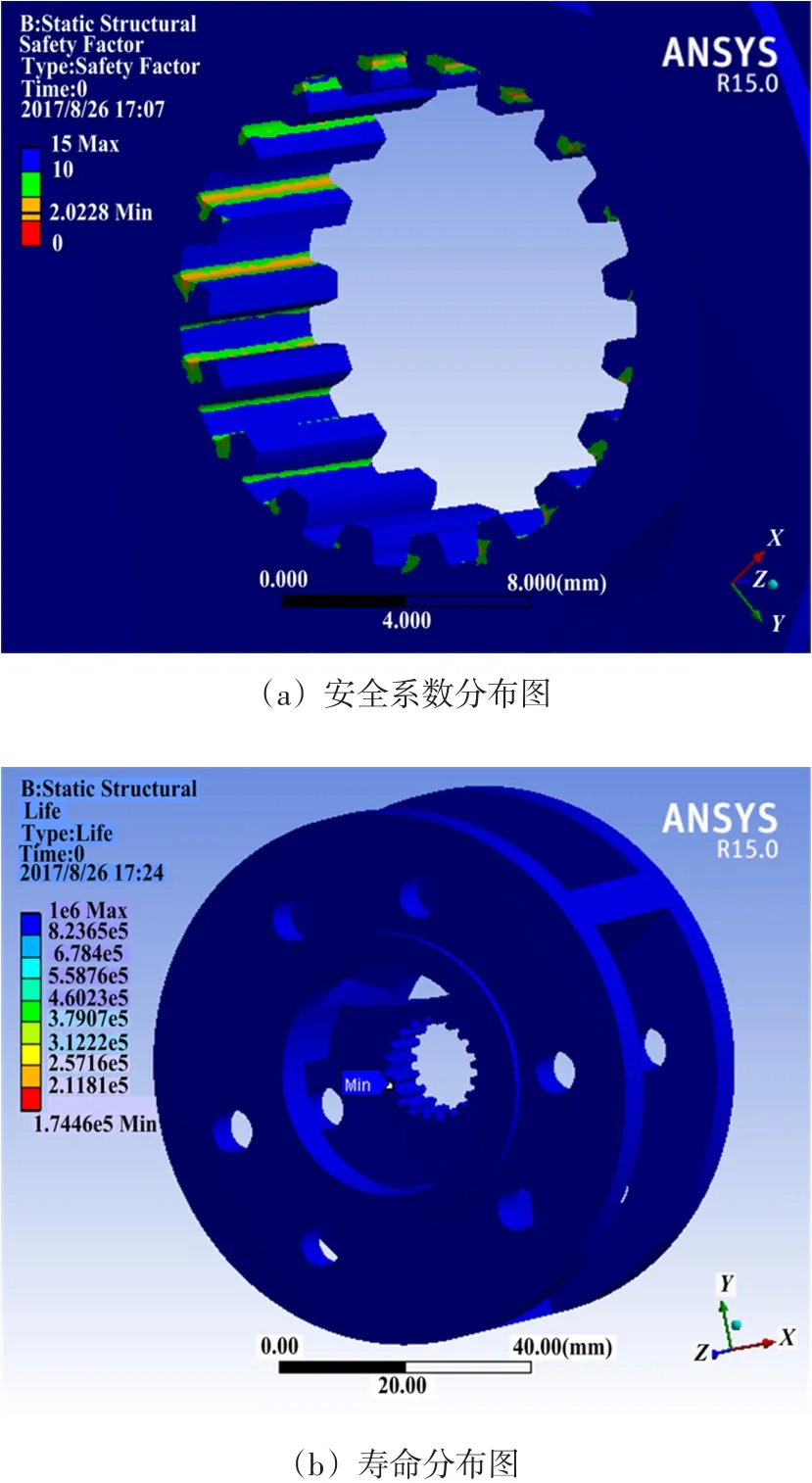
图8 安全系数与疲劳寿命分布云图Fig.8 Safety factor and fatiguelifedistribution nephogram

由图8得出，寿命最小位置与静态分析结果（最大应力出现位置）一致，均发生在中心板齿根处，值为1.7446e5小时，约等于1.7446e5÷24÷365=19.62年，满足服役时间15年的要求。最小安全系数为2.022 8，达到航空材料安全系数范围（1.5～3.0）的要求。

4.2 随机变量的统计处理

考虑行星架设计参数的分散性与材料属性的影响，以重要尺寸、弹性模量（E）作为可靠性分析的输入参数。均值取其名义尺寸，1/3的允许偏差为标准差，弹性模量由其变异系数（取为0.035）得到，同时假设它们的分布类型均为正态分布[15]。表3为可靠性分析输入随机变量的统计特性。

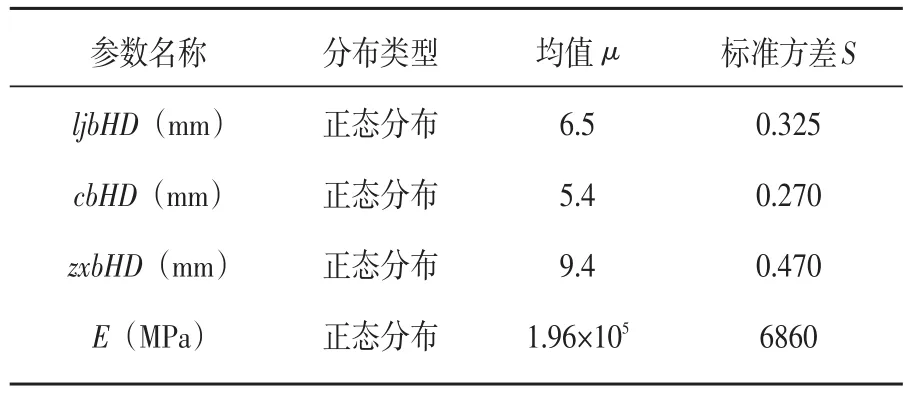
表3 随机变量的统计特性Tab.3 Statistical propertiesof randomvariables

通过分析得出输入参数对最小寿命的影响曲线，如图9所示。

图9 输入参数对最小寿命的影响Fig.9 Influenceof input parameterson lifeminimum

由图9可见，zxbHD对寿命影响最大，而且随着其增大最小寿命也一直延长；其次为ljbHD与cbHD，初始它们对寿命的影响趋势一致，寿命都随着它们的增大而延长，到了某个响应点以后，随着cbHD的增大寿命减小，而ljbHD的影响变得不显著；材料弹性模量（E）的影响不明显。

4.3 可靠性分析结果

通过反复调试抽样次数，最终当进行3 000次时输出变量的分布柱状图没有较大的间隙与跳跃，表明此抽样次数合适。计算得到图10所示最小寿命累计分布函数与概率列表。累计分布函数能够反应所有样本点所对应的概率值，通过对它的描述，可以得到结构的可靠度。

图10中黑色实线表示概率从0%～100%的分布函数，容易看出，最小寿命成指数分布集中在0.15×106～0.4×106（小时）之间，这段区间的概率达到90%以上，再结合概率列表来更准确的描述对应的概率值，看出最高概率达到99.977%。

图10 最小寿命累计分布函数与概率列表Fig.10 Cumulativedistribution function and probability list of lifeminimum

5 结论

详细分析了飞机襟翼EMA行星架载荷状况，针对同时满足多目标要求，采用基于响应面的多目标遗传算法求解行星架多目标优化问题，得到较好的静动态性能和轻量化效果。

优化后等效应力降低10.36%；固有频率增加0.78%；质量减少5.54%，产品的使用性能和经济性均得到提高。

对优化后的行星架进行疲劳与可靠性分析，得出行星架最小寿命、设计参数、材料性能对最小寿命的影响情况，画出最小寿命累计分布函数并算出其可靠性概率，满足寿命要求的可靠度达到90%以上。

参考文献：

［1］史佑民，杨新团.大型飞机高升力系统的发展及关键技术分析［J］.航空制造技术，2016，505（10）：74-78.

［2］韩复振.襟缝翼EMA高功率密度驱动系统研究［D］.西安：西北工业大学，2016.

［3］Zhong S，Chen Y，Zhou J，et al.An interactive satisfic⁃ing approach for multi-objective optimization with uncer⁃tain parameters ［J］.Journal of Intelligent Manufactur⁃ing，2017，28（3）：535-547.

［4］吉星宇.大功率EMA伺服驱动系统设计与研究［D］.南京：南京航空航天大学，2016.

［5］Benaouali A，Kachel S.An automated CAD/CAEintegra⁃tion system for the parametric design of aircraft wing struc⁃tures ［J］.Journal of Theoretical&Applied Mechan⁃ics，2017，55（2）：447-459.

［6］张晓辉，冯蕴雯，冯元生.基于可靠性的某型飞机襟翼刚度优化设计［J］.机械科学与技术，2010（08）：1076-1079.

［7］Antonelli M G，Bucci G，Ciancetta F，et al.Automatic test equipment for avionics electro-mechanical actuators（EMAs） ［J］. Measurement，2014，57（11）：71-84.

［8］Wu W，Lin Y R，Chow L C，et al.Electro-mechanical actuator fan fail⁃ure analysis and safety-critical de⁃sign ［J］.IEEE Aerospace and Electronic Systems Magazine，2017，32（4）：18-25.

［9］ Yi P X， Dong L J， Shi T L.Multi-objective genetic algorithms based structural optimization and ex⁃perimental investigation of the plan⁃et carrier in wind turbine gearbox［J］ .Frontiers of Mechanical Engi⁃neering， 2014， 9 （4） ：354-367.

［10］ Li X，Sun J.Genetic algorithm-based multi-objective optimization for statistical yield analysis under parame⁃ter variations［J］.Journal of Circuits Systems&Com⁃puters，2017，26（01）：1750009.

［11］ Wang N，Zhou Y J.Research on reliability of a hybrid three-redundant electro- mechanical actuator ［J］.Power Electronics，2011（02）：11-16.

［12］龚天强.基于有限元仿真的结构疲劳寿命预测及试验研究［D］.长沙：湖南大学，2013.

［13］ Ibrahim M H， Kharmanda G， Charki A.Reliabili⁃ty-based design optimization for fatigue damage analysis［J］.International Journal of Advanced Manufacturing Technology，2015，76（5-8）：1021-1030.

［14］ Li Y，Hu M，Wang F.Fatigue life analysis based on six sigma robust optimization for pantograph collector head support［J］ .Advances in Mechanical Engineer⁃ing，2016，8（11）：1-9.

［15］谢里阳，王正，周金宇，等.机械可靠性基本理论与方法［M］.北京：科学出版社，2012.