网壳结构的应用及研究现状

季 跃

(同济大学建筑设计研究院(集团)有限公司,上海 200092)

0 引 言

网壳结构具有跨度大、造型优美、节省材料、自重轻、便于工业化和标准化等诸多优点。随着世界杯和奥运会等体育运动盛会及世博会等大型活动的需要,网壳结构体系在全世界得到迅速发展。结构跨度愈来愈大,建筑创意与建筑风格的多样化,既反映出时代的特点,同时也对结构技术提出了巨大挑战[1]。目前,网壳形式种类繁多,在网壳结构的设计中,应合理选取网壳形式,在满足建筑形态与功能要求的同时,做到安全可靠、施工方便和经济合理。稳定问题是网壳结构设计中的主要问题。网壳结构发展至今,有许多结构因失稳而造成结构倒塌,其中最为典型的是1961年建成的罗马尼亚布加勒斯特穹顶倒塌案例,该网壳的破坏原因在于过量积雪导致结构发生局部失稳,而后通过失稳传播导致整体的大变形,最终造成了结构的跳跃型整体失稳破坏。由此,网壳结构的稳定问题得到了国内外广大研究者的重视。本文对网壳结构的形式与应用、失稳模态、稳定性能影响因素以及稳定承载力的研究现状进行了回顾,总结出已取得的研究成果以及尚需进一步深入研究的问题,期望为实际工程应用和理论研究提供可参考的综合分析资料。

1 网壳结构的应用

钢结构网壳结构最早可追溯到1863年,有“穹顶之父”之称的德国人Schwedler设计建造了第一个钢网壳结构。近年来,随着钢材和铝合金性能的改进、计算技术的飞速发展以及施工工艺水平的提高,网壳结构已广泛应用于机库、航站楼、车站站房、体育馆、展览馆、会堂、游泳馆、煤棚等建筑中。表1列举了国内外部分具有代表性的网壳结构,图1为其工程应用实例。

表1具有代表性的网壳结构信息

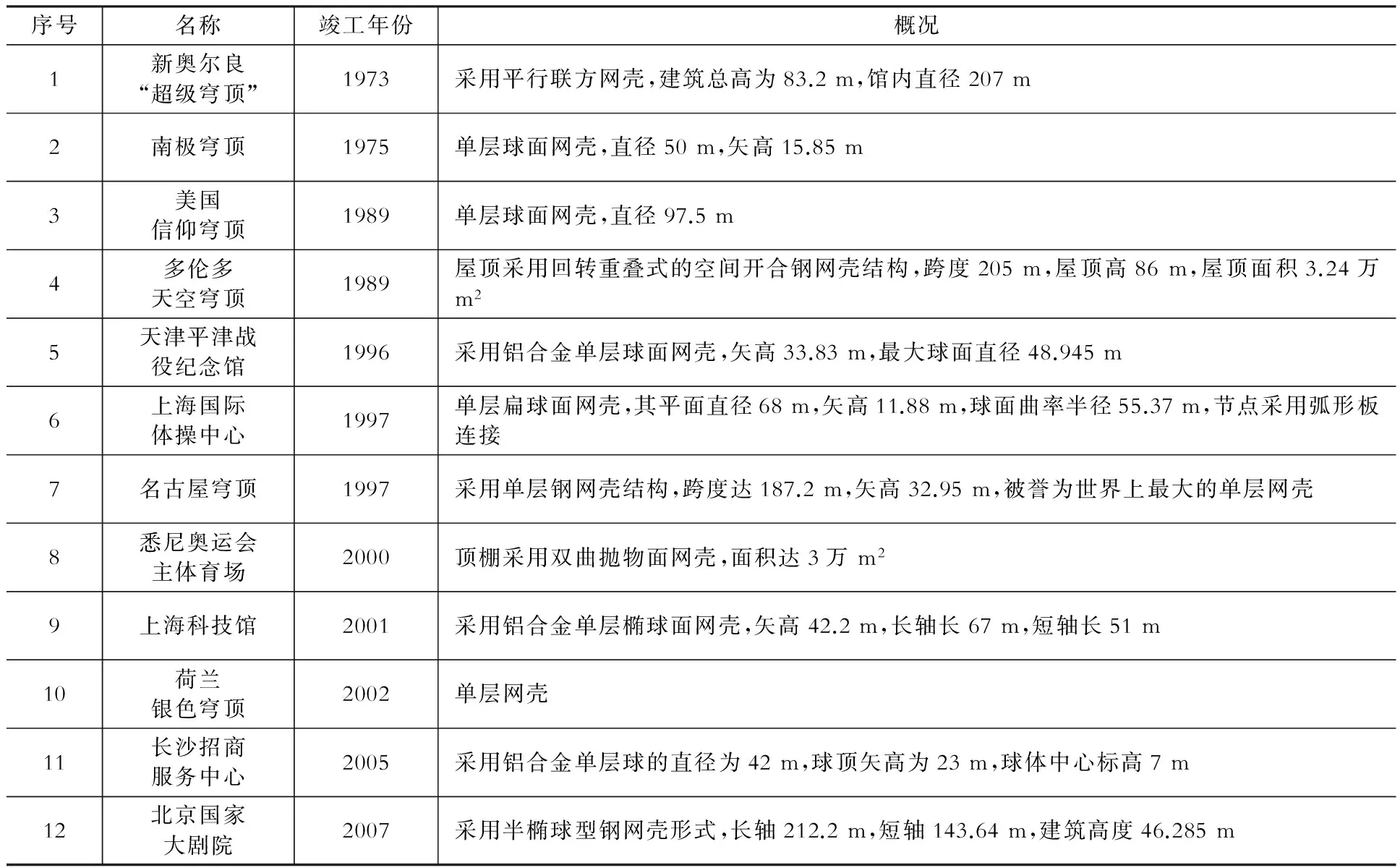
Table Information of several representative reticulated shells

图1 具有代表性的网壳结构Fig.1 Several representative reticulated shells

2 网壳结构整体稳定影响因素

网壳结构的整体稳定性是网壳结构设计中最主要的问题之一,国内外研究学者对其进行了大量的研究[2-3]。影响网壳稳定性能的主要因素有矢跨比、节点刚度、杆件初弯曲、材料性能、荷载分布模式和初始缺陷。

2.1 矢跨比的影响

网壳结构的失稳类型与其矢跨比相关。罗永峰等[4]指出,对于面内刚度较大的网壳,例如凯威特型和三向网格型网壳,它们的失稳类型主要与矢跨比有关。矢跨比大易发生分支型失稳,矢跨比小则出现极值型失稳,随着矢跨比由大到小变化,网壳的失稳类型由分支型失稳向极值失稳过渡。曹正罡等[5]对132例矢跨比为1/4～1/2的K8型单层球面网壳进行弹性、弹塑性稳定性能分析,结果显示,大矢跨比情况下,初始几何缺陷的存在会导致网壳的极限承载力降低50%,材料非线性对极限承载力的影响也明显大于常用矢跨比情况,塑性折减系数达到0.4,网壳极易提前发生失稳,并建议适当提高大矢跨比球面网壳的稳定性验算安全系数。

2.2 节点刚度的影响

近年来,节点刚度对网壳整体稳定性能的影响是建筑结构领域的热点研究课题之一。在网壳结构的设计中,结构的稳定性问题较为突出。我国的《空间网格结构技术规程》(JGJ 7—2010)[6]规定,在分析双层网壳结构时,节点假定为铰接;分析单层网壳时,节点假定为刚接。然而,现有的研究成果表明,大多数网壳结构的节点实际上属于一种半刚性节点,节点刚度大小对结构的整体稳定性有很大影响[7]。

在国外,节点刚度对网壳稳定的影响研究起步较早。1995年,Lopez等[8]考虑节点半刚性的影响对网壳整体稳定性能进行研究指出,当节点刚度很低时,网壳结构的临界荷载特别敏感。1998年,Kato等[9]提出了考虑节点体刚性域和节点半刚性的杆件单元力学模型。2000年,Hiyama等[10]建立考虑节点半刚性的网壳有限模型,有限元结果与试验结果吻合较好。2012年Kitti[11]通过数值模拟指出,单层网壳跨度越大,节点半刚性对其稳定影响越大,节点的平面内弯曲刚度对单层网壳结构稳定具有重要意义。

目前国内有许多研究学者对不同类型半刚性节点网壳结构稳定都进行了大量研究。2008年,邱志国等[12]对相贯节点肋环型网壳进行分析,研究显示,相贯节点的半刚性对肋环型网壳的变形和稳定影响非常大,其中轴向刚度影响最大。2008年,康菊等[13]对半刚性节点短程线型网壳进行研究指出,在网壳结构稳定验算时,节点刚度和初始缺陷都不容忽视,但当节点刚度大于107Nm/rad时,节点刚度可以假定为刚性。2009年,范峰等[14]对螺栓球节点凯威特型网壳进行了系统的分析,指出影响网壳稳定的主要因素有节点抗弯刚度、跨度、矢跨比、杆件截面尺寸及荷载分布形式,而节点域、节点扭转刚度和支承条件的影响不大。2015年,马会环等[15]对半刚性螺栓球节点柱面网壳进行了试验研究和有限元模拟,考虑节点半刚性后,两者结果吻合较好。2016年,熊哲[16]对半刚性铝合板式节点网壳进行了试验研究和有限元模拟,指出在加载初期,节点体刚性域对网壳稳定承载力具有提高作用,但是由于节点半刚性的影响,半刚性节点网壳会先于节点刚接网壳发成失稳破坏。同时,通过大量数值模型算例发现,节点刚度对网壳整体稳定承载力的影响不仅跟节点刚度有关,同时还跟网壳的等效抗弯刚度和矢跨比有关。

2.3 杆件初弯曲的影响

杆件初弯曲是一种典型的初始几何缺陷,可明显降低细长压杆的稳定承载力。李国强等[17]提出了一种考虑初弯曲影响的非线性梁单元,并对其矩阵进行推导。周臻等[18]推导了考虑初始弯曲的非线性杆单元表达式,通过索拱结构算例指出,杆件初始弯曲对结构极限承载力影响较大。范峰等[19-20]提出了判断杆件初弯曲的两种方法,并研究了杆件初弯曲对网壳结构弹塑性稳定性能影响,结果表明,杆件初弯曲将明显降低结构承载力,并且能够改变结构的塑性发展程度。杆件初弯曲对单层网壳弹塑性稳定性能的影响不可忽略。

2.4 材料性能的影响

材料性能对网壳整体稳定承载力具有极大影响。《空间网格结构技术规程》[6]指出,单层网壳的塑性折减系数(即网壳弹塑性极限荷载与弹性极限荷载之比)从统计意义上可取0.47。范峰等[21]对2000多例钢网壳进行了弹塑性整体稳定性分析,统计分析得到短程线型钢网壳的塑性折减系数为0.43;K6型钢网壳的塑性折减系数为0.46;施韦德勒双向斜杆钢网壳的塑性折减系数为0.491;施韦德勒单向斜杆钢网壳的塑性折减系数为0.44;葵花型刚网壳的塑性折减系数为0.528;肋环型网壳的塑性折减系数为0.8。曹正罡等[22]对600多例单层柱面钢网壳的弹塑性稳定性能进行研究,指出柱面钢网壳塑性折减系数取值范围为0.362～0.578。铝合金与钢材的材性有显著不同,因此,钢网壳的塑性折减系数不适用于铝合金网壳的设计。熊哲[16]对K6型铝合金网壳的弹塑性整体稳定性能进行分析指出,铝合金网壳的塑性折减系数取值为0.689～0.799;半刚性的铝合金板式节点网壳的塑性折减系数取值为0.848～0.94。

2.5 荷载分布模式的影响

在网壳结构的设计时,需要考虑多种荷载组合,荷载分布在大多数情况下是不对称的,且非对称荷载通常是不利的荷载分布,对结构的受力性能可能会有明显影响。张春丽等[23]研究了荷载非对称分布对联方型单层球面网壳稳定性的影响,结果表明,荷载的反对称性进一步降低了结构的稳定承载力,当p/g(半跨活荷载与均布恒荷载的比值)为0.25时,网壳承载力降至均布荷载时的75%～89%;当p/g为0.5时,网壳承载力降至均布荷载时的67%～82%;当p/g为1时,网壳承载力降至均布荷载的54%～62%。结构的稳定承载力随p/g的增大而减小,且下降幅度较大。张峰等[24]对不同长度的单层柱面网壳结构进行了非对称荷载作用下的全过程稳定分析,并指出当柱面网壳l/b(长宽比)≤1.2时,荷载非对称分布引起柱面网壳极限荷载的降低;当柱面网壳l/b>1.2时,荷载非对称分布对柱面网壳的极限荷载没有影响。

2.6 初始缺陷的影响

实际网壳结构中,初始缺陷不可避免。影响网壳结构整体稳定的初始缺陷主要是网壳几何形状的初始偏差,即节点实际位置的偏差。大量研究表明,结构的初始缺陷对结构整体稳定承载力的影响十分巨大[25-26]。范峰等[21]指出,施加L/300的网壳一阶屈曲模态缺陷,单层球面钢网壳的整体弹塑性稳定承载力下降至0.4～0.7之间。熊哲[16]对K6型铝合金板式节点网壳弹塑性整体稳定进行研究,指出L/300的初始缺陷对网壳整体稳定承载力的削弱作用随着矢跨比的增大而提高。当网壳矢跨比从1/7增大至1/4时,初始缺陷影响系数取值范围为0.286～0.333。

现阶段,引入初始缺陷的有效方法主要有一致缺陷模态法和随机缺陷模态法。1984年,Kani[27]提出一致缺陷模态法,求解网壳结构的失稳模态,并将其引入到实际结构中,结果显示结构的失稳形式将转化为极值点失稳。1986年,See等[28]将完善结构的第一阶屈曲模态引入到结构中,得到的计算结果与试验值比较接近。2007年,罗昱[29]研究发现,对于单层浅网壳的稳定承载力起控制作用的不仅是网壳的第一阶屈曲模态缺陷分布形式;对于矢跨比较小、跨度较大的单层网壳结构的稳定性起控制作用的往往是高阶的屈曲模态缺陷分布形式。因此罗昱提出了改进的单层浅网壳一致模态缺陷分析方法,对于单层浅网壳的分析应该在考虑多阶屈曲模态缺陷分布形式的同时考虑多阶屈曲模态缺陷分布形式的耦合作用,并给出了简单的耦合作用公式。随机缺陷模态法是从概率统计的观点出发,假定每个节点的安装误差符合正态分布,可用正态随机变量对其进行模拟。把结构的初始安装缺陷看作一个多维随机变量,其样本空间的每一个样本点都对应着结构的一种缺陷模态。1988年,Borri等[30]采用蒙特卡洛法模拟缺陷的大小和分布,分别比较了杆件对节点的初偏心缺陷和几何形状的初偏差对网壳结构整体稳定性的影响,结果显示,几何形状的初偏差对结构整体稳定性的影响远大于杆件初偏心的影响。

3 网壳结构整体稳定承载力

现有关于网壳结构整体稳定承载力的研究主要包括数值方法、试验研究和承载力公式。

3.1 数值方法

目前非线性有限元理论和梁柱单元理论已成为网壳结构非线性稳定分析的常用数值方法。1973年Oran[31]在梁柱理论的基础上,考虑轴向力对弯曲的影响以及弯曲变形对杆件长度变化的影响,推导出杆件单元切线刚度矩阵表达式。1998年Kato等[9]推导了考虑节点体刚性域、节点半刚性和杆件塑性铰的空间梁单元刚度矩阵表达式。随着ANSYS、ABAQUS等非线性有限元软件的问世,网壳结构的有限元模拟逐渐广泛应用于结构设计分析中。范峰等[32]在ANSYS中建立了考虑节点体刚性域、节点非线性刚度的杆件单元力学模型。郭小农等[33]总结了八种在有限元软件中用到的考虑节点刚度的杆件单元力学模型。在网壳结构整体稳定分析中,如何得到结构的完整荷载-位移曲线是全过程分析技术主要需要解决的问题。Newton-Raphson法及其改进方法[34]能够有效地追踪荷载-位移曲线的上升段,但却无法获得其下降段,因此该方法在全过程分析中失效。为了获得全过程曲线,研究学者基于Newton-Raphson法的理论基础,提出了人工弹簧法、位移控制法、弧长控制法、当前刚度法、自动求解技术和能量平衡技术等一系列有效方法[35]。文献[36]指出,修正的Crisfield等弧长法是跟踪全过程屈曲路径最有效的方法。

3.2 试验研究

关于试验研究,Lopez等[37]通过两个网壳的承载力试验结果验证,提出了适用于ORTZ节点体系的杆件单元力学模型。Hiyama等[10]通过试验研究分析铝合金螺栓球节点单层球面网壳的稳定性能。为了研究铝合金板式节点球面网壳的承载性能,曾银枝等[38]进行试验分析,结果显示,节点的刚度对网壳整体稳定性能的影响不能忽视。罗永峰等[39]对单层网壳结构弹塑性稳定性能进行试验研究,结果显示,网壳结构的失稳具有缺陷敏感性,并且部分杆件的塑性变形对其稳定性能及承载能力有着显著影响。为考察上海东方明珠国际会议中心单层球网壳的承载能力,赵宪忠等[40]进行了1:10缩尺模型试验。试验结果表明,在设计荷载作用下,结构反应基本为线性行为。马会环等[15]对柱面网壳的承载能力进行了试验分析,其承载力介于节点刚接网壳和节点铰接网壳之间。熊哲[16]对铝合金板式节点网壳进行了试验研究,指出该网壳属于一种加载初期超刚性,加载后期节点半刚性网壳。

3.3 承载力公式

网壳结构稳定承载力的理论分析大多基于连续化的拟壳法。1999年沈世钊[41]通过2800余例各式网壳的全过程分析,揭示了不同类型钢网壳结构稳定性能的基本特性,并提出了单层球面网壳、柱面网壳和椭圆抛物面网壳稳定性承载力的实用计算公式所示。值得注意的是,这些公式仅考虑网壳几何非线性稳定承载力,并未考虑材料非线性的影响。

Lopez等[42]以两杆件平面结构为基础,推导单层网壳承载力公式(式(1)),公式中反映出了节点刚度和网壳几何因素对承载力的影响。

(1)

式中,n为网壳的径数;E为材料的弹性模量;A为杆件的截面面积;γA为考虑荷载种类的影响系数;γL为考虑荷载分布的影响系数;θ0为同一径内相邻杆件间夹角的一半,小于45°;为杆件长细比;为节点的刚度系数,为LK/(6EI+LK),L为杆件长度,K为节点刚度。

范峰等[43]对半刚性节点的凯威特型网壳的弹塑性整体稳定承载力进行了大量有限元模拟,得到考虑螺栓球节点半刚性和材料弹塑性的网壳承载力公式,如式(2)所示。

(2)

式中,γq为考虑荷载分布的影响系数;ki为拟合系数;R为网壳曲率半径;B为等效薄膜刚度;D为等效抗弯刚度。

马会环等[44]推导了考虑螺栓球节点半刚性和材料弹塑性的椭圆抛物面网壳承载力公式,如式(3)-式(5)所示。

(3)

kq=1/[1+0.956(p/g)+0.076(p/g)2]

(4)

β=a(1-e-bα)

(5)

式中,cp为塑性折减系数,三向网格型椭圆抛物面网壳取0.79,单向斜杆正交网格型椭圆抛物面网壳取0.89;k0为承载力修正系数,三向网格型椭圆抛物面网壳取2.55,单向斜杆正交网格型椭圆抛物面网壳取1.78;kq为荷载分布修正系数;R1和R2为网壳两个主轴方向曲率半径;p/g是半跨活荷载与满跨恒荷载的比值;β是节点半刚性对网壳等效抗弯刚度D的影响系数,其具体影响参考文献[45];α是节点刚度系数,为节点初始刚度与杆件线刚度的比值。

4 结 语

伴随着网壳结构在建筑领域越来越广泛的应用,广大研究学者们对网壳整体稳定性能影响因素及其承载力的试验和理论研究也越来越深入及全面,目前已取得一些突破,但仍有许多工作要做:

(1) 网壳结构节点种类形式繁多,现阶段主要探讨了螺栓球节点、相贯节点和铝合金板式节点刚度对网壳整体稳定性能的影响。其他常用节点的刚度对网壳整体稳定性能的影响有待进一步研究。

(2) 材料性能对网壳结构整体稳定性能具有极大影响,而且与矢跨比和节点刚度相关。目前规范[2]中给出的材料塑性折减系数基本上参考钢网壳的统计结果,并未体现矢跨比及节点刚度的影响。另外,由于铝合金材料性能与钢材有着显著差异,钢网壳的塑性折减系数显然不适用于铝合金网壳的设计。关于铝合金网壳结构的塑性折减系数有待进一步研究。

(3) 对于网壳整体稳定承载力研究,目前对钢球面网壳、双曲抛物面网壳的研究较为成熟,而对钢柱面网壳和铝合金网壳整体稳定承载力的研究有待进一步加强。

[1] 范重,杨苏,栾海强.空间结构节点设计研究进展与实践[J].建筑结构学报,2011,32(12):1-15.

Fan Zhong,Yang Su,Luan Haiqiang.Research progress and practice of design of spatial structure joints [J].Journal of Building Structures,2011,32(12):1-15.(in Chinese)

[2] Ma H H,Fan F,Shen S Z.Numerical parametric investigation of single-layer latticed domes with semi-rigid joints[J].Journal of the International Association for Shell and Spatial Structures,2008,49(2):99-110.

[3] Zugasti A M A,Lopez A,Puente I.Influence of geometrical and structural parameters on the behaviour of squared plan-form single-layer structures[J].Journal of Constructional Steel Research,2012,72:219-226.

[4] 罗永峰,宋谦.不同矢跨比单层球面网壳的稳定性态[J].建筑钢结构进展,2005,7(2):37-42.

Luo Yongfeng,Song Qian.Stability behavior of single-layer spherical reticulated shells with different ratio of height to span[J].Progress in Steel Building Structures,2005,7(2):37-42.(in Chinese)

[5] 曹正罡,范峰,沈世钊.大矢跨比单层球面网壳弹塑性稳定性研究[J].哈尔滨工业大学学报,2008,40(2):183-186.

Cao Zhenggang,Fan Feng,Shen Shizhao.Elasto-plastic stability of large rise-span ratios single-layer reticulated domes[J].Journal of Harbin Institute of Technology,2008,40(2):183-186.(in Chinese)

[6] 中华人民共和国住房和城乡建设部.JGJ 7—2010空间网格结构技术规程[S].北京:中国建筑工业出版社,2010.

Ministry of Housing and Urban-Rural Development of the People’s Republic of China.JGJ 7—2010 Technical Specification for space frame structures[S].Beijing:China Architecture and Building Press,2010.(in Chinese)

[7] 郭小农,沈祖炎.半刚性节点单层球面网壳整体稳定性分析[J].四川建筑科学研究,2004,30(3):10-12.

Guo Xiaonong,Shen Zuyan.Analysis of stability of single-layer spherical reticulated shells with semi-rigid joints[J].Sichuan Building Science,2004,30(3):10-12.(in Chinese)

[8] Lopez A,Gerald K.The effect of joint stiffness on the buckling behavior of reticulated dome structures[C].Asia-Pacific Conference on Shell and Spatial Structures,CCES-IASS.Beijing,1996,21-25.

[9] Kato S,Mutoh I,Shomura M.Collapse of semi-rigidly jointed reticulated domes with initial geometric imperfections[J].Journal of Constructional Steel Research,1998,48:145-168.

[10] Hiyama Y,Takashima H,Iijima T,et al.Buckling behaviour of aluminium ball jointed single layered reticular domes[J].International Journal of Space Structures,2000,15(2):81-94.

[11] Kitti G.Effect of connection rigidity on the behaviour of single-layer steel grid shells[C].Conference of Junior Researchers in Civil Engineering,Budapest,Hungary,2012:58-65.

[12] 邱国志,赵金城.相贯节点刚度对肋环型网壳结构整体稳定性的影响[J].工业建筑,2008,增刊:1023-1029.

Qiu Guozhi,Zhao Jincheng.Influence of joint stiffness on stability behavior of ribbed reticulated spherical shells[J].Industrial Construction,2008,S1023-1029.(in Chinese)

[13] 康菊,宋振森.节点刚度对有缺陷短程线球面网壳稳定性的影响[J].四川建筑科学研究,2008,34(1):42-46.

Kang Ju,Song Zhensen.The influence of joint stiffness on the stability of geodesic single-layered reticulated shells with initial imperfection[J].Sichuan Building Science,2008,34(1):42-46.(in Chinese)

[14] 范峰,马会环,沈世钊.半刚性型螺栓球节点单层K8型网壳弹塑性稳定分析[J].土木工程学报,2009,42(2):45-52.

Fan Feng,Ma Huihuan,Shen Shizhao.Elasto-plastic stability analysis of K8 single-layer reticulated shells with bolt-ball joint system[J].China Civil Engineering Journal,2009,42(2):45-52.(in Chinese)

[15] Ma H H,Fan F,Wen P,et al.Experimental and numerical studies on a single-layer cylindrical reticulated shell with semi-rigid joints [J].Thin-Walled Structures,2015,86:1-9.

[16] 熊哲.铝合金板式节点单层网壳整体稳定性研究[D].上海:同济大学,2016.

Xiong Zhe.Study on the global buckling behavior of single-layer latticed shells with aluminium alloy gusset joints[D].Shanghai:Tongji University,2016.(in Chinese)

[17] 李国强,刘玉姝.一种考虑初始缺陷影响的非线性梁单元[J].计算力学学报,2005,22(1):69-72.

Li Guoqiang,Liu Yushu.A nonlinear beam element considering initial imperfection[J].Chinese Journal of Computational Mechanics,2005,22(1):69-72.(in Chinese)

[18] 周臻,孟少平,吴京.一种考虑杆件初始弯曲的非线性杆单元[J].东南大学学报(自然科学版),2007,37(2):201-205.

Zhou Zhen,Meng Shaoping,Wu jing.Nonlinear link element considering member initial curvature[J].Journal of Southeast University,2007,37(2):201-205.(in Chinese)

[19] Fan F,Yan J C,Cao Z G.Stability of reticulated shells considering member buckling[J].Journal of Constructional Steel Research,2010,77:32-42.

[20] Fan F,Yan J C,Cao Z G.Elasto-plastic stability of single-layer reticulated domes with initial curvature of members [J].Thin-Walled Structures,2012,60:239-246.

[21] Fan F,Cao Z G,Shen S Z.Elasto-plastic stability of single-layer reticulated shells[J].Thin-Walled Structures,2010,48:827-836.

[22] 曹正罡,孙瑛,范峰,等.单层柱面网壳弹塑性稳定性能研究[J].土木工程学报,2009,42(3):55-59.

Cao Zhenggang,Sun Ying,Fan Feng,et al.Elasto-plastic stability of single-layer cylindrical reticulated shells[J].China Civil Engineering Journal,2009,42(3):55-59.(in Chinese)

[23] 张春丽,李正良,赵一,等.荷载非对称分布对单层球面网壳稳定性的影响[J].重庆建筑大学学报,2004,26(2):63-67.

Zhang Chunli,Li Zhengliang,Zhao Yi,et al.Effect of unsymmetrical loading distribution to the stability of single-layer latticed domes[J].Journal of Chongqing Jianzhu University,2004,26(2):63-67.(in Chinese)

[24] 张峰,沈世钊.荷载非对称分布对单层柱面网壳稳定性的影响[J].哈尔滨建筑大学学报,1998,31(1):31-36.

Zhang Feng,Shen Shizhao.The effect of unsymmetric loading distribution to the stability of single-layer lattice vaults[J].Journal of Harbin University of C.E.& Architecture,1998,31(1):31-36.(in Chinese)

[25] Yamada S,Takeuchi A,Tada Y.Imperfection-sensitive overall buckling of single-layer lattice domes[J].Journal of Engineering Mechanics,2001,127:382-386.

[26] Suzuki T,Ogaw T,Toda I,et al.Elastic buckling analysis of rigidly jointed single-layer reticulated domes with random initial imperfection[J].International Journel of Space Structure.1992,7(4):265-273.

[27] Kani I M,McConnell R E,See T.The analysis and testing of a single layer,shallow braced dome[C].3rd International Conference on Space Structures.1984,613-618.

[28] See T,McConnell R E.Large displacement elasic buckling of space structures[J].Journel of Structure Engineering,1986,112 (5):1052-1069.

[29] 罗昱.改进的一致缺陷模态法在单层网壳稳定分析中的应用研究[D].天津:天津大学,2007.

Luo Yu.Research on the advanced consistent mode imperfection method for single-layer domes stability analysis[D].Tianjin:Tianjin University,2007.(in Chinese)

[30] Borri C,Spineli P.Buckling and post-buckling behavior of single reticulated shells effect by random imperfection[J].Computer Structure,1988,30(4):937-943.

[31] Oran C.Tangent stiffness in space frames[J].Journal of the Structural Division,1973,99(6):973-985.

[32] 范峰,马会环,曹正罡.半刚性螺栓球节点空间网壳结构受力性能研究[J].建筑钢结构进展,2011,13(6):1-8.

Fan Feng,Ma Huihuan,Cao Zhenggang.Mechanical performance of single-layer reticulated shells with semi-rigid bolt-ball joints[J].Progress in Steel Building Structures,2011,13(6):1-8.(in Chinese)

[33] 郭小农,熊哲,罗永峰.空间网格结构节点刚度研究现状简述[J].结构工程师,2014,30(4):185-195.

Guo Xiaonong,Xiong Zhe,Luo Yongfeng.State-of-the-arts of research on the joint stiffness of the spatial structures[J].Structural Engineers,2014,30(4):185-195.(in Chinese)

[34] Meek J L,Tan H S.Ceometrically non-linear analysis of space frames by an incremental iterative technique[J].Computer Methods in Applied Mechanics and Engineering,1984,47:261-282.

[35] 钱若军.弹性结构非线性稳定全过程分析述评[C].空间网格结构论文集.上海:同济大学出版社,1991.

Qian Ruojun.A comment of the nonlinear stability analysis of elastic structures[C].Symposiums on Space Grid Structures and Reticulated Shells.Shanghai:Tongji University Press,1991.(in Chinese)

[36] Victor G.Buckling of reticulated shells:state-of-the-art[J].International Journal of Space Structures,1995,10(1):1-46.

[37] Lopez A,Puente I,Miguel A S.Numerical model and experimental tests on single-layer latticed domes with semi-rigid joints[J].Computers and Structures,2007,85:360-374.

[38] 曾银枝,钱若军,王人鹏,等.铝合金穹顶的试验研究[J].空间结构,2000,6(4):47-52.

Zeng Yinzhi,Qian Ruojun,Wang Renpeng,et al.Test research on the aluminous-alloy dome[J].Spatial Structures,2000,6(4):47-52.(in Chinese)

[39] 罗永峰,沈祖炎,胡学仁.单层网壳结构弹塑性稳定试验研究[J].土木工程学报,1995,28(4):33-40.

Luo Yongfeng,Shen Zhuyan,Hu Xueren.Experimental study on elastoplastic stability of single layer reticulated shells[J].China Civil Engineering Journal,1995,28(4):33-40.(in Chinese)

[40] 赵宪忠,沈祖炎,陈以一,等.上海东方明珠国际会议中心单层球网壳整体模型试验研究[J].建筑结构学报,2000,21(3):16-22.

Zhao Xianzhong,Shen Zhuyan,Chen Yiyi,et al.Experimental study on the overall single-layer spherical dome model of shanghai international convention center[J].Journal of Building Structures,2000,21(3):16-22.(in Chinese)

[41] 沈世钊.网壳结构的稳定性[J].土木工程学报,1999,32(6):11-19,25.

Shen Shizhao.Stability of latticed shells[J].China Civil Engineering Journal,1999,32(6):11-19,25.(in Chinese)

[42] Lopez A,Puente I,Miguel A S.Direct evaluation of the buckling loads of semi-rigidly jointed single-layer latticed domes under symmetric loading[J].Engineering Structures,2007,29:101-109.

[43] Fan F,Ma H H,Cao Z G,et al.Direct estimation of critical load for single-layer reticulated domes with semi-rigid joints[J].International Journal of Space Structures,2010,25(1):15-24.

[44] Ma H H,Fan F,Zhong J,et al.Stability analysis of single-layer elliptical paraboloid latticed shells with semi-rigid joints [J].Thin-Walled Structures,2012,72:128-138.