基于温度空间分布的传感节点部署最优化研究

，，，，

(1.苏州科技大学 江苏省建筑智慧节能重点实验室，江苏 苏州 215009；2.同济大学 电子与信息工程学院，上海 201804)

0 引言

相关研究表明，现代人类滞留室内时间超过生命周期的90%[1]。在影响室内环境舒适度的众多因素中，温度是极其重要的因子，其高低直接关系到室内人员的健康以及工作效率。

无线传感网(wireless sensor network, WSN)的敷设不需要基础设施的支持，通过电磁波将被测量传输至汇聚节点。与传统的有线传输方案相比，WSN对建筑结构破坏很少，能有效地避免了二次装修污染问题，是一种高效、可靠的室内温度实时采集方式。

相对于室外环境中普遍使用的动态WSN，室内空间结构等因素使得静态无线传感网成为首选。由于缺乏移动性，节点初始部署问题在静态无线传感网的敷设中至关重要，它直接关系到测量温度的准确性、完整性和时效性。

节点的部署最早可以追溯到O’Rourke提出的艺术画廊问题[2]。通过解画廊问题可以实现二维空间内初始覆盖的最优化。然而，数学方法获得的部署方案仅适用于规则区域。这与实际室内环境中办公、生活用品等障碍物普遍存在的客观现实不符，这一矛盾直接导致了数学解准确性的急剧下降[3]。许多学者提出通过局部的信息找到次优化方法，Meguerdichian等利用了Voronoi 图和Delaunay三角测量技术寻找最差路径和最有效路径[4-5]，Chakrabarty[6]和Meguerdichian等通过线性规划的方法，得到保持覆盖的最小活动(Active)节点集[7]； Couqueur团队提出了可扩展的容错的局部算法[8]。

考虑到被测量的时变特性，根据被测量的物理特性，B. Zhao团队使用了拉格朗日离散随机移动模型、漂移通量模型和混合模型等，对大型公共空间室内微环境中污染物浓度的扩散规律进行了研究[9]。另外，B. Zhao团队还提出了一个基于流体力学的三维模型，仿真了人体周围环境中0.5～10 μm粒径的粒子分布特点，通过研究发现，在空气流量相同的情况下，不同粒径的颗粒运动轨迹各不相同。

N. P. Gao团队建立了基于三维漂移通量模型、欧拉模型的混合仿真模型，提出了基于颗粒直径的分析方法，对室内空气中不同粒径粒子的分布进行了对比研究，得出结论，颗粒大小与其对人体影响程度成反比，即粒径越大，对人体健康的影响越小[10]。同时，N. P. Gao团队还提出了结合人体结构特征与流体力学的研究方法，用来分析人体不同部位颗粒物浓度和温度变化情况，其结论可以应用于个性化通风系统的设计和优化中[11]。

在国外，Dehbi经过研究发现室内障碍物附近湍流与其他位置不同，这个结论与传统的拉格朗日离散随机移动模型中的观点不同，虽然后续的仿真结果与实验数据虽然存在误差，但是其认为误差在可接受范围内[12]。Dehbi的观点与Z. F. Tia等的结论具有很高的相似性，后者同时使用LES模型与拉格朗日模型，对室内环境中污染物浓度进行了比较，实验结果表明，LES模型准确性优于拉格朗日模型，根本原因是拉格朗日模型缺乏对于阻碍物的分析[13]。Z. Zhang等认真、细致地研究了传统的拉格朗日模型中存在的问题，提出了通过增加室内环境中采样粒子的数量来提高模型准确性的方法，该方法以增加计算复杂度为代价，获取较高的准确性[14]。

虽然国内外学者在室内污染物的分布规律领域取得了丰富成果，但是温度本身的物理特性与其他室内污染物存在不同之处，因此上述成果仅能提供部分借鉴作用。目前学界和业界普遍认同的模型是计算流体力学模型(CFD)及其衍生模型。

1 计算流体力学模型仿真

1.1 仿真环境

图1所示为计算流体力学仿真环境，建筑功能为公共办公场所，大小为7 m*7 m，高度为3 m，测试环境中主要存在黄色与蓝色两种主要的障碍物，其材质分别为为木质台面和金属质边框。热源为一台立体式空调。

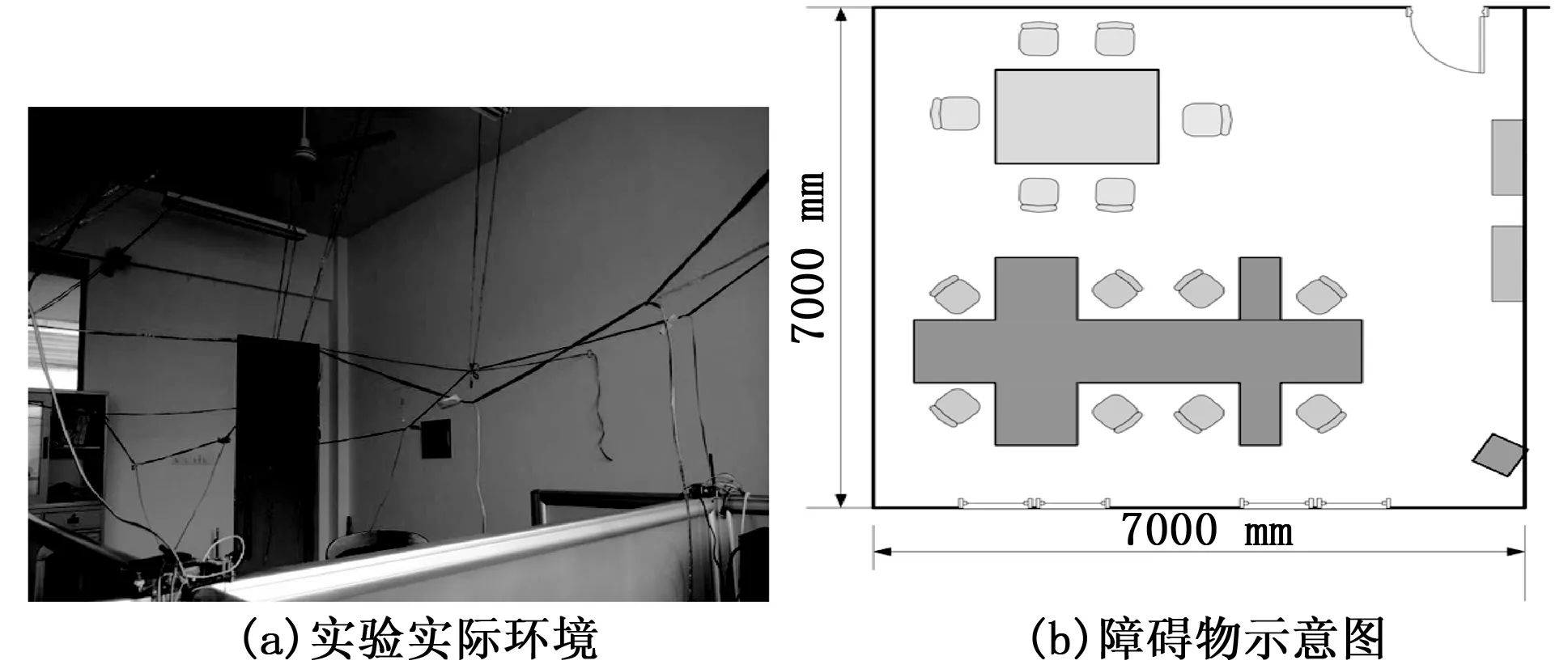
图1 办公室环境

1.2 仿真

FLUENT，是通用计算流体力学(computational fluid dynamics, CFD)软件包，它采用了多种求解方法和多重网格加速收敛技术，用来模拟从不可压缩到高度可压缩范围内的复杂流动，能达到最佳的收敛速度和求解精度。灵活的非结构化网格和基于解的自适应网格技术及成熟的物理模型，使FLUENT在转换与湍流、传热与相变等方面有广泛应用。

1.2.1 真参数设计

表1所示为FLUENT仿真参数设置，热源主要为立体式空调，房间初始温度为289 K，空调出风口温度为298 K，出射角为水平向上45°。首先讲模型环境进行网格化。

1.2.2 仿真过程

1) 建立网格化仿真模型:测量公共建筑空间三维数据，确定障碍物形状、尺寸及位置，建立公共建筑空间结构及障碍物三维模型。确定流体系统输入、输出口，构建流体模型拓扑结构，从流体模型表面切割出流体输入输出边界并进行关联，流体模型网格化，建立如图2所示的流体网格化模型。检测网格化完整度，确定模型坐标及单位，将所建模型导入FLUENT仿真器。

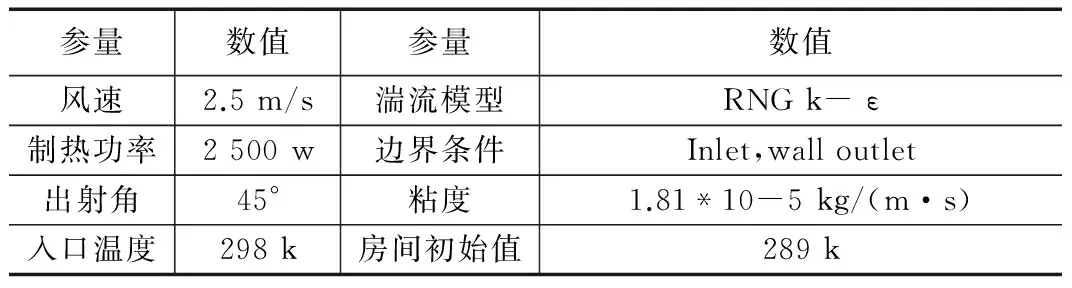
表1 仿真基本参数设置

图2 FLUENT网络化过程

2) 选择方程及模型:对于被测量时间、空间分布特性进行模拟分析的前提是建立能够准确描述空气流动规律的控制方程以及湍流模型，这些方程包括质量守恒、动量守恒、能量守恒。选择适当的湍流模型。设定流体模型为标准空气模型，入口类型定义为速度入口，并导入入口的实时参数，出口类型定义为压力出口，并设定初始温度，将剩余边界类型定义为标准墙体，完成模型设置。

3) 仿真运行条件设计及仿真结果获取:设定仿真环境工作大气压力、参考压力坐标(原点)、重力加速度，其他参数使用默认值。采用非定常模型仿真，设置仿真环境监视器，按需设定时间步长及迭代次数，开始仿真，生成各时间段内室内各切面等位线图，获取被测量时间分布规律。

重复上述1)～3)步骤，获取被测量空间分布规律。

2 实验结果分析

图3给出了使用FLUENT对室内温度变化情况的仿真。如图3(a)所示，当热源工作1分钟后，局部区域温度可以升高，但是温度并未形成扩散，只是集中在热源附近，但是温度存在明显的梯度变化，即温度呈现出热源向四周扩散的趋势。

2分钟后，在图3(b)中热源左侧的区域内，温度升高幅度较为显著，造成之一现象的主要原因是，热源的出风口主要朝向左侧，因此，热源左上方及右方的区域温度升高幅度不明显。

在第6分钟时，随着热度的进一步扩散，左上方区域温度明显提高，同时，热源附近的区域温度扩散进一步加快，温度从热源向外呈现出梯度下降的趋势。

随着热源发热状态的持续，在7分钟后，整个被测区域除左侧及右侧少许地方，其他区域温度都有所升高，热源附近升温较快区域面积基本保持不变。造成左右两侧温度变化较小的主要原因是建筑结构，在测量区域中间顶部，有一道横梁，由于出风口出射角为水平向上45°，因此热风遇到横梁形成反射，造成横梁区域温度升高较快，而左侧升温反而很慢。在测量区域右侧，由于处在热风影响区域以外，所以温度升高幅度缓慢。

10分钟后，热源影响持续扩大，左侧区域温度升高较快，由于出风口位置的影响，下方的区域温度升高幅度最为明显，但是右上方区域内，温度变化不大。整个被测区域的温度呈现下方向上方的扩散，且梯度较为明显。

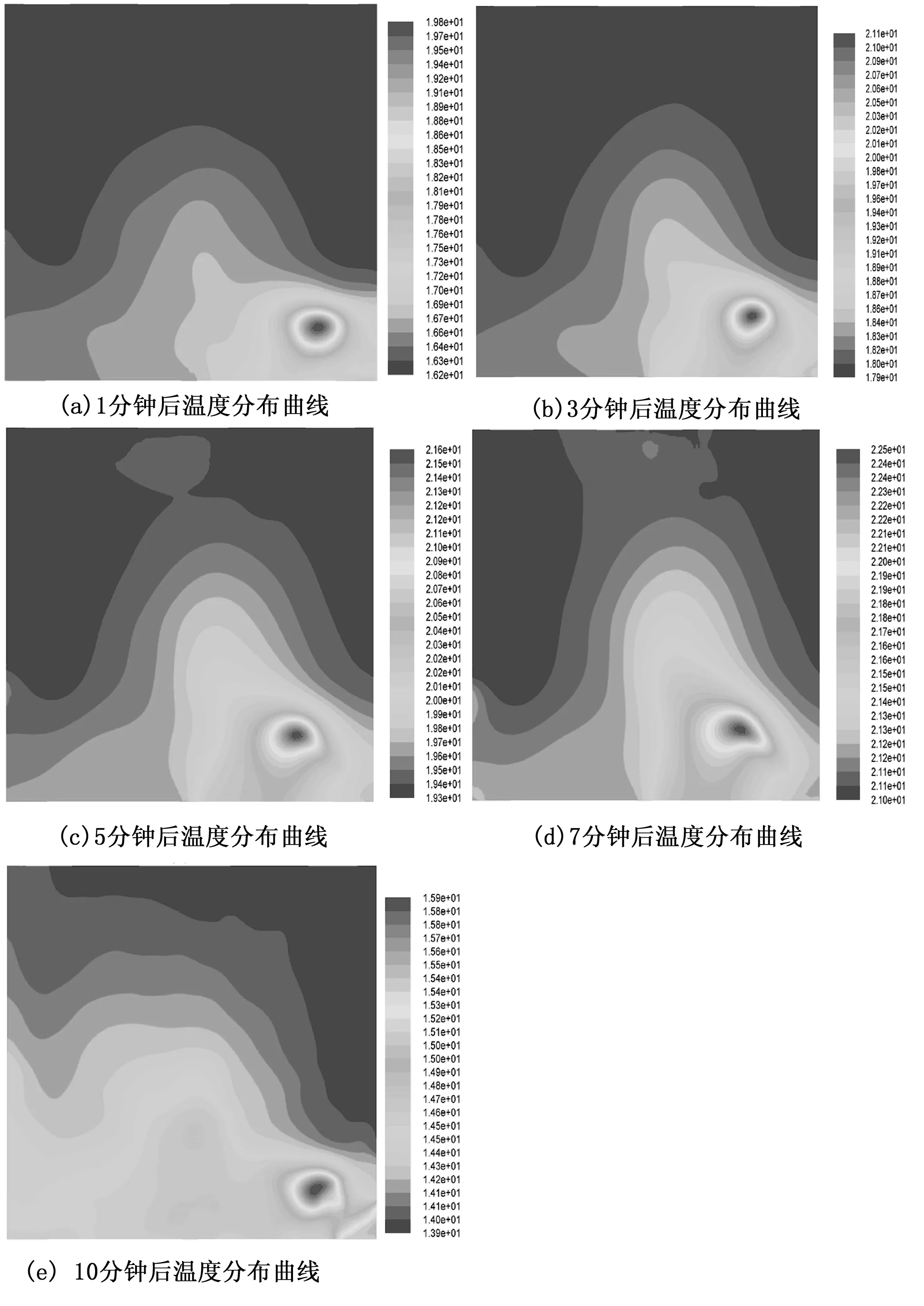
图3 FLUENT仿真结果

3 算法

图3给出了随着时间变化，温度的梯度变化情况，可以看出，温度非均匀变化，部分区域温度变化速率较快，部分区域变化不明显或者无变化，但是局部环境的变化速率基本一致，因此，可以在局部区域内设置一个传感节点，测量数据可代表区域内的温度变化特征，即

YDL≤yi≤YDH

(1)

式中，(xi,yi)和(xj,yj)代表i点和j点的位置，ηi(xi,yi)和ηj(xj,yj)分别为i点和j点的温度，β是测量精度，XDL和XDH为区域在X方向上的2个端点，YDL和YDH为区域在Y方向上的2个端点。若测量点温度与某区域内所有节点的温度差异不超过β，则可以认为改区域内任意一点都可以代表整个区域的温度分布情况。

4 算法实践及结果分析

4.1 实验基本设置

根据式(1)以及图3中结论，将整个测量空间分成如图4所示的4个区域，以A、B、C和D标示，每个区域放置若干传感节点，测量结果通过无线传输模式传送到终端，便于后续数据处理及分析。实验重复10次，结果取10次测量的平均值。

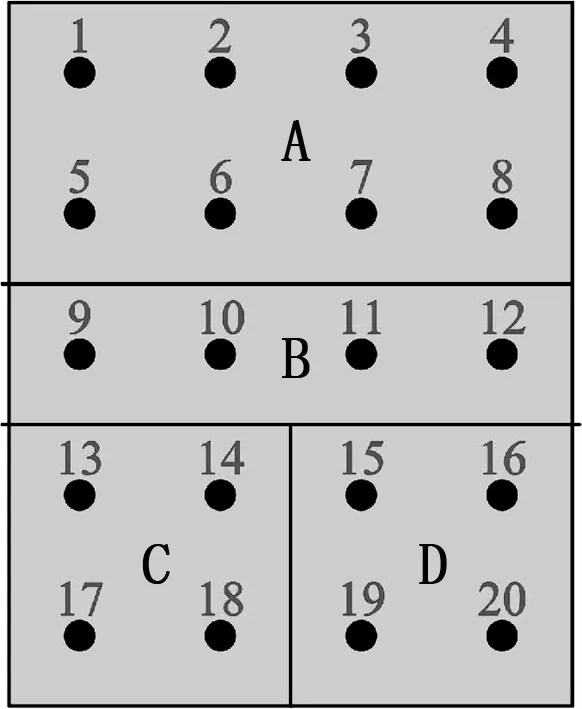
图4 分区传感器敷设节点图

传感节点放置在离房间顶部1.0 m、离地面2.0 m处，避免障碍物对热风的反射作用。表2给出了实验的参数设置。如表所示，使用发射功率为1 mw的蓝牙模块作为无线传输模块，采样频率为1 Hz，即每秒采样一次，采样个数为600个。

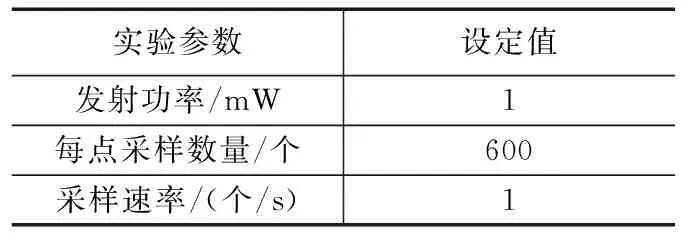
表2 具体参数设置

4.2 实验结果及分析

图5给出了A、B、C和D 4个区域温度测量结果的平均值。如图5(a)所示，在1分钟时，A区域内节点测量结果非常接近，最大差异不超过3%。在3分钟后，节点6和节点7的温度略高于其他节点，与图3(b)中结果一致。5分钟后，节点8测量温度最低，节点4的温度比节点8温度略高，其余节点温度差异不大。7分钟后，节点5温度测量值较低。10分钟后，所有测量温度趋于一致，差异不超过1 ℃，测量结果与仿真结果基本保持一致。

图5(b)给出了9～12号节点的测量结果，其中10号节点测量值在各个时间段内始终高于B区域内的其他节点，而节点11的测量值始终处于最低值。在观察期1分钟以及3分钟内，测量结果保持一致。在5分钟后，节点10处的温度明显高于其他3个节点，温差超过1 ℃，当持续到7分钟时，虽然节点10处的温度仍然保持最高，但是与9号和12号节点的温度差异进一步缩小，而11号节点的温度仍然保持最低，这一趋势一致持续到测量结束。

图5(c)中，在测量初期温度差异较大，随着热源的持续加热，温度差异呈变小趋势。在初始阶段，节点13处温度最低，节点14测量温度最高。随着测量的继续，虽然节点13温度的测量值仍然是最低的，但是其值于节点14处的差异逐渐缩小，约为0.7 ℃。当测量5分钟后，节点18处温度成为最低值，节点13处温度变为最高，但是两者差异小于0.2 ℃，虽然后续测量过程中，节点18与节点13处温度差异变大，但是其最大保持在0.5 ℃以下，造成这一现象的主要原因是，实验过程中，无关人员在不了解情况下，打开了窗户，使得节点18处的温度变低，虽然后续采取了补救措施，但是节点18处的温度仍处于缓慢升高状态。

图5(d)各点中，节点15测量的温度明显高于同区域其余3个测量节点，且随着测量时间的增加，差异变大。在1分钟时刻，D区域内4个节点温差不大，主要原因是热源刚开始扩散，不足以影响各个测量节点，当测量持续三分钟后，15号节点的测量值增加幅度大于其余节点，随着观察时间的增加，节点15处的时间-温度曲线的斜率明显大于其余3个节点，至测量1分钟时，节点15与D区域内其余3个节点的温差达到了3 ℃。

综上所述，在区域A中，8个节点温度变化不明显，因此可以用一个节点的测量值预估整个区域的温度，差错率最大为4%。在区域B中，4个节点的温度差异约为1 ℃，用一个节点代替其余节点，误差维持在6%以下。图C中在初始时刻节点间温度差异不超过1 ℃，若要求精度保持在10%以内，则用一个节点可以代替其余节点的温度变化状态及趋势，若精度要求在5%以内，则需要2个节点。在D区域内，若测量精度要求20%以内，则仅需一个节点即可以解决，若精度要求低于10%，则需2个节点。

图5 实验测量结果

5 结论

计算流体力学模型能够有效地对室内温度的变化情况进行仿真，结果具有可重复的特点。依据计算流体力学仿真结果，结合无线传感网测量结果，给出了一种温度静态传感网初始节点位置的算法，根据精度差异，给出最小节点数量以及各个节点的具体位置。实验结果表明，当精度要求低于10%时，仿真区域内最少敷设5个节点即可以满足测量要求，在保证精度的同时，最大限度的节约成本。算法不仅为温度静态传感网节点初始位置设定提供了方法，也可以为其他物理量的测量提供理论依据。

参考文献：

[1] Luo H, Wang N, Chen J P, et al. Study on the thermal effect and air quality improvement of green roof [J]. Sustainability, 2015 (7):2804-2817.

[2] Edelsbrunner H, O’Rourke J, Welzl E. Stationing Guards in Rectilinear Art Galleries[A]. Proceedings of Computer Vision, Graphics and Image[C]. 1984, 27:167-176.

[3] Slijepcevic S, Potkonjak M. Power efficient organization of wireless sensor networks[A]. Proceedings of the IEEE Conference on Communications[C]. 2001, 472?476.

[4] Meguerdichian S, Koushanfar F, Potkonjak M, et al. Coverage problems in wireless Ad-hoc sensor networks[A]. INFOCOM'01[C]. 2001, (3): 1380-1387.

[5] Meguerdichian S, Koushanfar F, Qu G, et al.. Exposure in wireless Ad hoc sensor networks [A]. Proceedings of 7th Annual International Conference on Mobile Computing and Networking[C]. 2001, 139-150.

[6] Chakrabarty K, Iyengar S. S, Qi H, et al.. Grid coverage for surveillance and target location in distributed sensor networks [J]. IEEE Transactions on Computers, 2002, 51(12): 1448-1453.

[7] Bulusu N, Heidemann J, Estrin D. Adaptive beacon placement[A]. Proceedings of the 21th International Conference on Distributed Computing Systems[C]. 2001,489-498.

[8] Couqueur T, Phipatanasuphorn V, Ramanathan P, et al. Sensor deployment strategy for target detection [A]. Proceeding of The First ACM International Workshop on Wireless Sensor Networks and Applications, WSNA’02[C]. 2002:42-48.

[9] Zhao B, Yang C Q, Yang X D, et al. Particle dispersion and deposition in ventilated rooms: Testing and evaluation of different Eulerian and Lagrangian models[J]. Building and Environment, 2008, 43(4):388-397.

[10] Zhao B, Guan P, Modeling particle dispersion in personalized ventilated room[J]. Building and Environment, 2007,42(3):1099-1109.

[11] Gao N P, Niu J L. Modeling particle dispersion and deposition in indoor environments[J]. Atmospheric Environment, 2007, 41(8):3862-3876.

[12] Gao N P, Zhang H, Niu J L. Investigating indoor air quality and thermal comfort using a numerical thermal manikin[J]. Indoor and Built Environment, 2007, 16(1):7-17.

[13] Dehbi A. A CFD model for particle dispersion in turbulent boundary layer flows[J].Nuclear Engineering and Design, 2008, 238(3):707-715.

[14] Tian Z F, Tu J Y, Yeoh G H, et al. Numerical studies of indoor airflow and particle dispersion by large Eddy simulation[J].Building and Environment, 2007, 42(10): 3483-3492.