基于递推最小二乘的吊舱推进无人水面艇建模与辨识研究

,,,

(大连海事大学 信息科学技术学院，辽宁 大连 116026)

0 引言

无人水面艇(Unmanned Surface Vehicle, USV)可以作为河流水质监测、水面舰艇跟踪和现代化军事武器，用来执行危险以及不适合人员参与的任务，具有广泛的市场前景，己成为了国内外智能化海洋装备的研究热点[1]。在复杂多变的海洋环境以及军事对抗中，往往需要USV具有较快的航速以及良好的机动性，这就对其推进器的性能提出了较高的要求。吊舱式推进器(POD)是近几年发展起来的一种新型船舶推进装置，该装置可以节省船体空间、增加有效载荷、提高船舶推进效率和操纵灵活度，是船舶推进领域最有发展前途的新技术之一[2]。POD推进器可以绕轴线作360度回转，在任何方向上产生矢量推力，不需要舵和侧推器[3]的情况下就能够实现船舶回转、倒车以及横向移动等驾驶操作。所以对于USV而言，采用POD推进器不仅满足其基本操纵需求，更可以提高USV综合航行性能。

但相对而言，POD推进还是一种新型推进技术，尽管国内外陆续发表一些关于POD研究的文献，但大多数都只是对其本身的性能进行研究。日本学者Tomihiro Haraguchi[4]等采用航向改变和航向保持的性能来评价POD推进船舶的操纵性。英国学者Michael D Woodward[5]对POD推进船舶的性能进行了预报。马骋[6]以POD推进器为研究对象，运用数值计算和模型试验两种方法，对其水动力性能进行分析并对POD推进船舶的实船性能进行预报。针对POD推进的半潜船，惠子刚[7]建立其三自由度模型并对其半潜船性能进行预报，但未对所建模型的精度进行验证。文献[8]应用MMG分离建模思想，建立配备吊舱推进器的半潜船四自由度运动数学模型并将其运用到航海模拟器中。文献[9]在分析电力吊舱推进船舶的机械特性的基础上，建立了MMG三自由度模型，在一定程度上解释了吊舱推进船舶的操纵运动特性。但是在船舶控制器设计过程中，应用最为广泛的是其响应型数学模型，所以本文首先对POD推进USV的响应模型进行建模。

为研究POD推进USV操纵运动控制技术，首先需要建立其相对准确的数学模型。在已知模型结构的基础上，本文采用辨识建模的方法确定模型参数。文献[10]首次将SVM方法应用于船舶操纵运动建模，为系统辨识技术在船舶操纵运动建模方面提供了新的方法。文献[11]通过拖曳实验采集数据，采用最小二乘辨识MMG模型参数，然后通过反向自适应辨识剩余参数，经验证辨识结果准确有效，但此方法只可适应于模型船只且方法过于繁琐。文献[12]提出了通过不同的操纵运动来辨识小型无人艇的模型参数，并用费舍尔矩阵来评价辨识结果的优劣。文献[13]针对一艘高速三体模型船，在已知部分船舶模型参数的基础下，首先使用逐步回归法辨识未知系数，然后通过基于无迹卡尔曼滤波的非线性预测误差法对之前的辨识结果进行优化。文献[14]基于径向基神经网络及其逼近能力，在未知的海洋环境下提出了一套对海洋水面舰艇进行精确识别和学习控制的方法。大部分文献对浆-舵推进的船舶模型进行辨识研究，而少有文献研究POD推进船舶的响应模型辨识。

本文以大连海事大学“蓝信”号POD推进USV为研究对象，首先采用MMG分离建模的思想建立其三自由平面运动数学模型，然后对艇体受力和推进器推力进行分析和假设的基础上，将三自由模型化简为反应推力角与艏摇角速度的响应模型。在得到响应模型的基础上，通过实船实验采集回转实验和Z型实验数据，以系递推最小二乘以及数据拟合的方法得到模型参数。最后对辨识结果进行模拟仿真并与实船数据进行比较，以此验证建模与辨识的正确性，为一类吊舱推进船舶的建模及其模型辨识提供了理论基础以及一套简单有效的方案。

1 USV建模

鉴于运动数学模型的建立是研究无人艇运动控制性能的基础，所以建立复杂度适宜，同时精度也符合USV运动控制要求的数学模型是十分必要的。权衡之下，本文决定采用MMG分离型建模思想对“蓝信”号USV进行建模。

1.1 USV及其推进系统

“蓝信”号是大连海事大学一艘集水样采集、海洋监测、海上救援等功能为一体的智能化小型快速无人水面艇。

“蓝信”号USV推进器采用的是美国水星(MERCURY)公司的BRAVO系列推进器[6]。该推进器集推进和操舵于一体，从原理上是一种吊舱推进器。

1.2 USV平面运动模型

研究USV在海洋上运动，按惯例采用附体坐标系和惯性坐标系。如图1所示，O-X0Y0Z0是惯性坐标系，o-xyz是附体坐标系。在航行过程中一般情况包括前进速度u、横漂速度v、起伏速度w，艏摇角速度r、横摇角速度p及纵摇角速度q六个自由度的运动，ψ表示航向角，δ表示推力角。

图1 两种坐标系中USV运动描述

根据现有经验，对于USV 6个自由度的运动，可以忽略起伏、纵摇及横摇运动，即认为船舶做平面运动，即w=p=q=0。在假设船舶前后对称和附体坐标系的原点在船舶重心的前提下，可以将六自由度的MMG模型化简成三自由度的平面运动模型。

(1)

其中：m为船舶重量，mx为x轴方向的附加质量，my为y轴方向的附加质量，Izz为ox轴的惯性矩，Jzz为z轴方向上的附加惯性矩。X，Y，N分别为作用在船体上的流体动力和力矩，H为作用于裸船体流体动力，P推进器推力。

1.3 模型化简与推导

根据文献[15]，作用于裸船体流体动力为：

(2)

其中：YNL，NNL是非线性流体动力，相对于线性流体动力而言可以认为其为高阶小量，可以直接忽略不计。根据文献[16]，推进器推力为：

T=cVδn+d|δn|δn

(3)

T为推进器推力，δn为螺旋桨转速，c和d为相应常数。当推力角为δ时，各个方向的矢量推力分别为

(4)

其中：xδs为从旋转中心到推进器支点的纵向力臂长度。假设在小扰动下，即USV始终运动在初始平衡状态附近，此时作用在艇体上的线性流体动力占主导地位，而高阶项项量级较小可以忽略。在船舶模型研究领域，一般把船舶的匀速直线运动作为初始平衡状态，假设u=u0，v=v0=0，r=r0=0，δ=δ0=0，其中u0为无人艇的纵向初始速度。无人艇受到外界干扰后，运动状态变化量为Δu，Δv=v，Δr=r和Δδ=δ，从而运动状态变为u=u0+Δu，v=v0+Δv，r=r0+Δr，δ=δ0+Δδ。此时方程(1)化简为：

(5)

下面讨论在存在扰动的情况下USV上的流体动力。保留一阶小量Δu，v，r和δ，忽略二阶及以上的高阶小量。

(6)

X(u0+Δu)为无人艇直航阻力，可以表示为：

(7)

Ct为总阻力系数，其本质为航速的函数。将公式(7)展开得：

(8)

Ct0为航速为u0时的总阻力系数，对式(8)的Δu进行线性化处理得：

(9)

其中：X0为USV在初始状态下的直行阻力。则XH=X0+XHuΔu，即：

(10)

考虑到δ为小量，所以sinδ≈δ，cosδ≈1。公则式(4)可以化简为：

(11)

因为在初始状态下，USV所受阻力等于推进器推力，所以X0+XP=0，即公式(12)可以化简为式(13)：

(12)

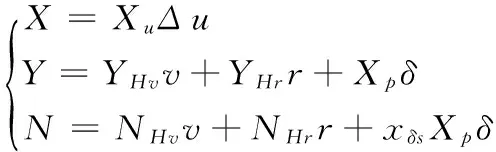
(13)

将式(13)代入式(1)得：

(14)

假设USV受到小扰动时，纵向速度不变，所以X，Y和N可以解耦分开考虑。所以式(14)可以分解为：

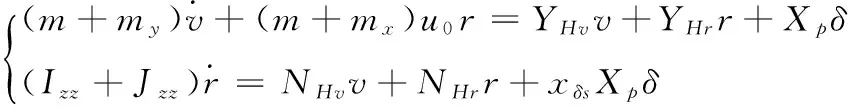
(15)

令YHv=Yv，YHr=Yr，Xp=Yδ，NHv=Nv，NHr=Nr，xδsXp=Nδ，所以式(15)可以化简为：

(16)

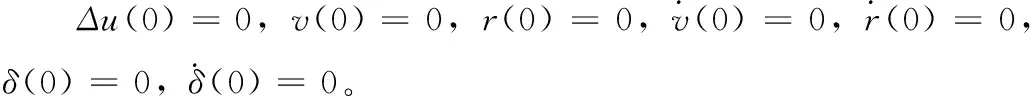
(Izz+Jzz)sr(s)=Nvv(s)+Nrr(s)+Nδδ(s)

(17)

将频域内艏转角速度对舵角的关系，经拉普拉斯逆变换，可转换成时域线性响应方程：

(18)

其中：

(19)

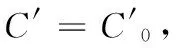
(20)

其中：α为新引入的常量且αr3体现非线性影响。将公式(20)化简为一阶系统形式，即：

(21)

由此可见：POD推进USV在本质上依然与普通的螺旋浆-舵推进船舶一样，依然符合Norrbin模型结构。

1.4 推进系统伺服模型

通常情况下，推进角改变过程的响应模型通常被视为一阶惯性环节，即：

(22)

其中：时间常数为Tr，对于“蓝信”USV而言约为1.2 s；目标推力角为δr。但在实际航行中由于推进器与水流的相互作用，导致推力角存在非常明显的振荡。因此，本文根据实际情况，不将伺服系统的响应模型按一阶惯性环节处理，立足于实验过程所采集的实艇数据，将伺服响应模型按二阶欠阻尼环节处理，即：

(23)

其中：ωn为自然频率，ζ为阻尼比，ξ为比例系数。

2 模型辨识

2.1 实验数据采集

为了保证实验数据的精确性，在相对平稳的海况下(一级海况)，USV分别以5°、8°、12°、15°、17°、18°、20°的推力角进行回转实验，航速稳定在8～10kn。由于记录数据较多，本文中只列出5°时的部分数据，如表1所示。

表1 5°回转实验数据

不同推力角下对应的平均转艏角速度如表2所示。

在相同的海况与航速约束下，进行15°/15°的Z型实验，部分数据如表3所示。

表2 推力角与艏摇角速度

表3 Z型实验数据

2.2 响应模型辨识

Norrbin模型的本质是Nomoto模型加上非线性项α。Nomoto模型如公式(24)所示：

(24)

首先通过Z型实验数据以递推最小二乘辨识Nomoto模型，即辨识出参数K和T。Nomoto辨识收敛曲线如图2所示。

图2 Nomoto辨识收敛曲线

a1～a3和b1～b3是离散传递函数的系数。传递函数如式(25)所示。

(25)

将式(25)转化为连续的传递函数式(26)：

(26)

从式(26)可以看出，高阶项与低阶项系数级别相差较大，所以可以省略高阶项，则式(26)变为：

(27)

将式(24)进行拉式变换得式(28)：

(28)

r+αr3=0.707δ

(29)

则可以通过艏摇角速度r和推力角δ拟合来确定参数α。经拟合α=0.001，拟合曲线如图3所示。

图3 δ和r拟合曲线

2.3 推进系统模型辨识

对于伺服响应模型，通过Z型实验的目标推力角与实际推力角以递推最小二乘进行辨识，收敛曲线如图4所示。

图4 伺服模型辨识收敛曲线

a1，a2和b1，b2是离散传递函数的系数。传递函数如式(30)所示：

(30)

将式(30)转化为连续的传递函数式(31)：

(31)

经化简：

(32)

即自然频率平均值为ωn= 0.958，阻尼比平均值为ζ= 0.811，放大系数平均值为ξ= 0.923。

3 辨识结果验证

3.1 回旋实验验证

以9kn的航速15°的推力角，利用辨识得到的Norrbin响应模型进行回转仿真实验，仿真结果如图5所示。15°推力角情况下，实船回转实验曲线如图6所示。

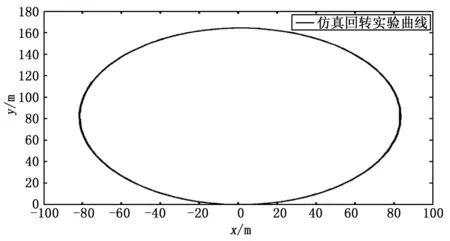
图5 回转实验仿真曲线

图6 实船回转实验曲线

从图5和6可以看出，USV的仿真稳定回转半径为84.3 m，实船稳定回转半径为82.5 m，绝对误差为1.8m，相对误差为2.2%，结果在可信范围内(20%)。从图7可以看出。即使在相对平稳的水面进行回转实验，但由于风浪流的存在，所以实际回转曲线产生了漂移现象。

3.2 Z型实验验证

以9 kn的航速15°/15°推力角进行Z型模拟仿真实验。图7和图8分别为一阶伺服系统下的仿真Z型实验和二阶伺服系统下的仿真Z型实验的结果。图9为实船Z型实验曲线。

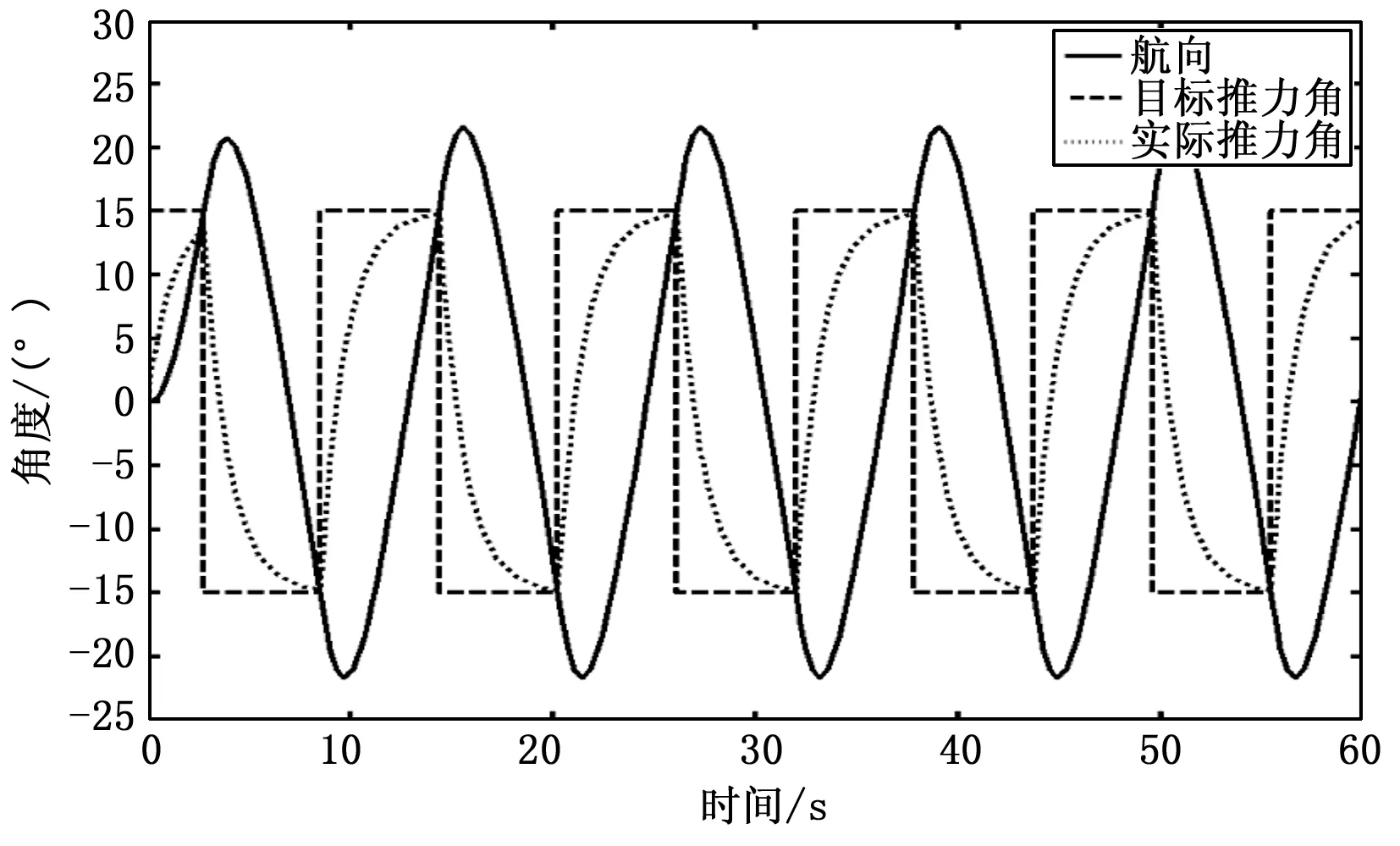
图7 一阶伺服Z型实验仿真曲线

图8 二阶伺服Z型实验仿真曲线

图9 实船Z型实验曲线

从图7、8和9可以明显看出，二阶伺服模型比一阶伺服模型更能较好地吻合实际推力角变化曲线。在二阶伺服模型下推力角的变化周期为12.6 s，而实船Z型实验的推力角变化周期为14.5 s，绝对误差为1.9 s，相对误差为13.1%，结果在可信范围内。

综上所述，在仿真情况下进行回转实验和Z型实验，经与实船数据相比误差在可信范围内，所以辨识的结果是相对准确的。由此证明，POD推进USV的建模与辨识的正确性。

4 结论

本文针对大连海事大学“蓝信”号吊舱推进无人艇，以响应模型建模与模型辨识为研究重点，对辨结果进行模拟仿真以此验证建模与辨识的正确性，仿真结果表明：

1)通过系统辨识的方法辨识出响应模型的参数，在此基础上进行仿真回转实验和Z型实验，并与实际回转实验和Z型实验进行比较，比较的结果为其相对误差分别为“2.2%”和“13.1%”，由此证明了由辨识得到模型的正确性。

2)在证明了辨识结果正确性基础上，进一步说明吊舱推进无人艇依然符合Norrbin模型结构这一结论的正确性。

建立吊舱推进无人艇的响应数学模型，并在此基础上进行系统辨识得到模型参数，可以为其操纵性能预报和智能控制奠定基础。在进一步的研究计划中，利用该模型设计USV航向控制器，并将此控制器运用到实船进行验证。

参考文献：

[1] Manley J E. Unmanned surface vehicles, 15 years of development[A].Oceans 2008[C]. IEEE, 2008: 1-4.

[2] 姚文龙. 船舶吊舱推进电机无模型自适应矢量控制策略研究[D]. 大连:大连海事大学, 2015.

[3] 陈伟民, 倪士龙. 全方位推进器与首侧推器综合作用对船舶操纵性能的影响[J]. 上海船舶运输科学研究所学报, 2005, 28(1): 11-14.

[4] Haraguchi T, Nimura T. A Study on Maneuvrability Standards for a Ship with a Pod Propulsion System[A].International Conference on Marine Simulation and Ship Maneuverability, MARSIM[C]. 2003, 3.

[5] Woodward M D, Clarke D, Atlar M. On the manoeuvring prediction of POD driven ships[A].International Conference on Marine Simulation and Ship Maneuverability (MARSIM 2003)[C]. Kanazawa, Japan. 2003.

[6] 马 骋. POD 推进器的水动力性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2006.

[7] 惠子刚. 半潜船操纵运动仿真研究[D]. 大连:大连海事大学, 2009.

[8] 张秀凤, 尹勇, 孙霄峰, 等. 吊舱推进船舶运动数学模型及其在航海模拟器中的应用[J]. 大连海事大学学报, 2013, 39(2): 9-12.

[9] Piao Z, Guo C. Maneuvering mathematical model and course control of POD-driven ship[A].2016 Sixth International Conference on Information Science and Technology (ICIST)[C]. IEEE, 2016: 301-305.

[10] Luo W L, On the modeling of Ship manoeuvring motion by using support vector machines, naval architecture and marine Engineering[D]. Shanghai Jiaotong University, 2009.

[11] Skjetne R, Smogeli O, Fossen T I. Modeling, identification, and adaptive maneuvering of Cybership II: A complete design with experiments[A].Proc. IFAC Conf. on Control Applications in Marine Systems[C]. 2004: 203-208.

[12] Wirtensohn S, Wenzl H, Tietz T, et al. Parameter identification and validation analysis for a small USV[A]. 2015 20th International Conference on Methods and Models in Automation and Robotics (MMAR)[C]. IEEE, 2015: 701-706.

[13] Herrero E R, Gonzalez F J V. Two-step identification of non-linear manoeuvring models of marine vessels[J]. Ocean Engineering, 2012, 53: 72-82.

[14] Dai S L, Wang C, Luo F. Identification and learning control of ocean surface ship using neural networks[J]. IEEE Transactions on Industrial Informatics, 2012, 8(4): 801-810.

[15] 贾欣乐, 杨盐生. 船舶运动数学模型: 机理建模与辩识建模[M]. 大连:大连海事大学出版社, 1999.

[16] Fossen T I. Nonlinear modelling and control of underwater vehicles[M]. Fakultet for informasjonsteknologi, matematikk og elektroteknikk, 1991.