基于小波分析的传感器故障诊断方法仿真研究

，，

(陆军装甲兵学院 控制工程系，北京 100072)

0 前言

在部队实际应用中，当装甲装备数据采集控制系统中的传感器发生故障时，必定对装备性能发挥造成严重影响，如果能有一种系统可以直接检测故障传感器并准确定位故障点，进而能尽快恢复系统的正常运行，将对战斗力的提升有着重大而深远的现实意义。一般的，在基于解析模型、基于知识和基于信号处理的三类基本故障诊断方法基础上，发展出的具体诊断方法有：解析冗余法、硬件冗余法、卡尔曼滤波器方法、基于小波分析的方法以及支持向量机的方法[1]等。本文研究的内容主要是利用小波变换的方法解决传感器故障，通过仿真试验及对试验故障数据的分析，验证了传感器故障检测中采用小波分析的方法的有效性和准确性。

1 小波分析的基本理论

将采集到的信号做分解处理，分解成由同一个小波母函数经过平移和尺度伸缩变换得到的一系列小波函数的叠加，这实际上就是小波分析的原理。与傅立叶分析的原理很相似，它也是把信号做分解处理，只是分解成的是叠加起来的一系列不同频率的正弦波[2]。所以说来，小波分析其实是把原始信号用多种小波基函数进行了分解。

对信号进行小波分解，设信号用f(t)表示，把它分解成一系列小波函数的叠加，需要经过三步。

首先要选取小波母函数Ψ(t)；第二步要将Ψ(t)做平移和伸缩的变换，进而得到一簇小波基函数Ψa,b(t)，a为伸缩因子，b为平移因子，如式(1)所示；第三步，对函数Ψa,b(t)和f(t)做卷积，得到小波变换的系数WTf(a,b)[3]。

(1)

1.1 连续小波变换

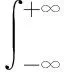
(2)

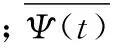
并不是所有小波函数都能被选为小波母函数，小波母函数基本的函数约束条件如下：

(3)

由式(2)可看出，小波变换是通过Ψ(t)在尺度上的伸缩和空间域(时域)上的平移来分析信号，因此，小波变换是一种空间-频率分析，它可以同时提供信号在时域和频域的局部描述，相比而言傅立叶变换则只能对信号全局进行描述。连续小波变换具有的特点是：时域和频域的局部定位，线性特性，自相似性和冗余性[4]。

1.2 离散小波变换

小波分析过程中，如果将平移因子a和尺度因子b按2的幂次离散化，即a和b都用离散的数值，那么此时得到的就是函数f(t)的离散小波变换，这里小波基函数Ψa,b(t)改写为：

(4)

其中:b0为大于零的实常数，j、k为整数，则离散小波变换为：

Wf(j,k) = 〈f(t),Ψa0 j,ka0 jb0(t)〉 =

(5)

离散小波变换实际上是将数字信号分解成一簇小波函数的加和，将小波基函数中的自变量参数进行离散化处理，把尺度因子按幂级数离散，即a=a0j；把时移因子均匀离散，即。j、k分别称为频率范围指数和时间步长指数，实际应用中，一般取a0=2，b0=1，这是一种经常被用到的二进制离散变换方式。

离散小波变换与连续小波相比，仍然具有一定的冗余度，但是比连续小波变换的冗余度大大降低。在进行数值的计算和图象处理、数据压缩等研究工作时，往往要求保持原信号f(t)信息的完整性，最大限度减小小波变换系数的冗余度，这时我们开展研究可以结合着连续小波变换和离散小波变换各自的特点进行。

1.3 连续小波变换的故障诊断原理

对传感器故障利用连续小波变换的方法进行检测诊断，本文给出如下思路：首先采集传感器系统的输入输出信号，并对所采集信号进行连续小波变换；其次，通过上述变换求出输入输出信号的奇异值；最后，找出因输入信号的突变而导致的极值点并加以去除，则剩下的极值点对应的就是传感器的故障。

先将要诊断的传感器假设成一个单输入单输出的线性系统，用线性系统参数的变化来模拟传感器的突变故障。如下式所示：

Y(s)=G(s)U(s)+ΔG(s)U(s)+E(s)

(6)

式中,Y(s)、U(s)、E(s)分别表示输出、输入和噪声信号的拉氏变换。G(s)表示传感器系统的传递函数，ΔG(s)表示系统的参数变化；E(s)表示平稳随机噪声，其均值为零。

再做假设u(t)为已知分段平稳随机信号，其故障与突变发生于不同时间；G(s)在原点处不存在零点和极值点，故障发生时，ΔG(s)≠0。

进行故障检测前，还要明确两点依据：一是对随机平稳信号它的小波变换均值为零，方差随尺度增大而逐渐趋于零[5]；二是未发生故障时，上述传感器系统输出信号的小波变换在尺度足够大时近似等于输入信号小波变换与系数K的乘积，即:

Wy(s,t)≈K*Wu(s,t)

(7)

其中:K在实际中一般用公式(8) 求得：

(8)

本文分两种情况讨论，第一种情况当输入信号均值不恒为零时，设系统残差有如下公式：

r(t)=Wy(s,t)-KWu(s,t)

(9)

此种情况下若系统未发生故障，由式(7)知，即使u(t)发生信号突变，随着尺度的增大残差r(t)也将趋于零。如果发生了故障，那么输出信号的均值就会发生突变，而输入信号瞬时是平稳信号，所以此时输出信号的小波变换随着尺度增大将出现明显的增大或缓慢衰减的极值点，同时输入信号小波变换将趋于零。

第二种情况当输入信号均值恒为零时，我们令：

r(t)=|Wy(s,t)|-|KWu(s,t)|

(10)

此时若系统未发生故障，同样由式(7)知，在尺度较大时输入信号的方差即使发生突变，残差也将趋于零。若发生故障，输出信号小波变换的方差和均值都将随着输出信号方差的变化而变化，而输入信号小波变换的均值由于输入信号瞬时平稳将保持不变，所以此时残差均值将发生变化，可利用残差的小波变换检测其突变点。

2 用连续小波变换方法检测传感器故障的Simulink仿真实例

本文建模仿真的内容均是在Matlab软件中利用Simulink工具完成的，用该工具建模较为直观，使用方便，软件中还包含小波分析的相关工具，对本文中传感器故障诊断的建模与仿真能够轻松实现。为了保证仿真实验的效果，接下来的仿真实验我们基于以下假设[6]：

1)文中研究的传感器出现故障仅限于系统正常工作的状态下，即假定仿真研究的全过程系统一直正常工作；

2)本文研究讨论的不是系统的全部动态过程，我们指的传感器故障诊断是针对系统的某一工况而进行的。

如前文所述，我们假定传感器为一个单输入单输出系统，设定其传递函数为：

(11)

2.1 传感器输入信号均值不恒为零时仿真研究

传感器正常工作时，设参数a=9,b=25,c=4,d=9。设在时间点t=140 s的时刻传感器发生故障，用c突变为6,d突变为25模拟突变故障，其余系数不变。输入信号u(t)的均值在时间t=60 s的时刻从0.5突变成2，干扰信号e(t)采用方差为0.1的高斯白噪声。设置完上述参数之后，第一次运行此仿真程序并取采样时间为0.03 s，得到图1所示的该系统输入输出信号波形。再选用db3小波对传感器进行故障检测，采样时间为0.03 s。得到各尺度下极值图如图2所示。

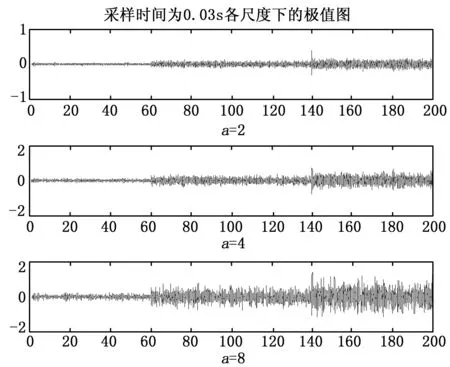
图2 各尺度下极值图

由图2可以看出，各尺度极值图在时间t=140 s时都出现了较为明显的突变，表明有故障的发生。但由于采样时间较大(0.03 s)，造成了其它时间段的噪声干扰过多，这也进而造成了极值图的诊断误差较大，导致检测出的故障点不准确。接下来我们把采样的时间设置为0.02 s，进行诊断时继续选用db3小波，得到多尺度下极值图如图3所示，再设置采样时间为0.01 s时作对比效果，如图4为采样时间为0.01 s时各尺度极值图。

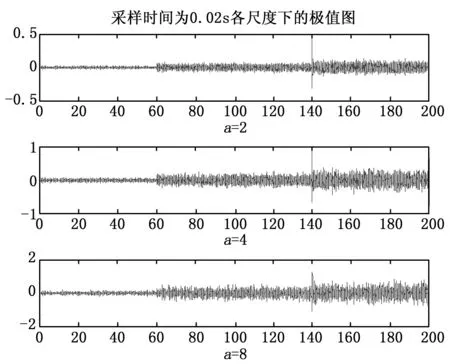
图3 采样时间为0.02 s时各尺度极值图

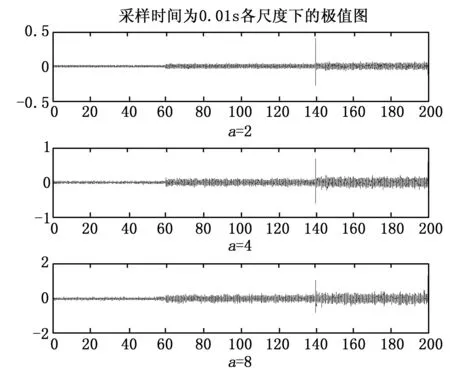
图4 采样时间为0.01 s时各尺度极值图

通过对不同采样时间下各极值图的对比可以看出，在提高了采样的频率后，各极值图都能够检测出故障的发生点，尤其采样时间为0.01 s时的故障发生点的直观性更明显。同时可以看到，由于没有对输入信号进行处理，噪声干扰导致了大量的干扰信号在其它时段的极值图中出现，显示到极值图上表现出波动较大的特性。下面我们选取采样时间为0.01 s时的故障诊断仿真实验为例，先对输入输出信号做40点的平滑处理，如图5所示，对图5中得到的信号，我们继续选用db3小波处理，得到多尺度下极值如图6所示。

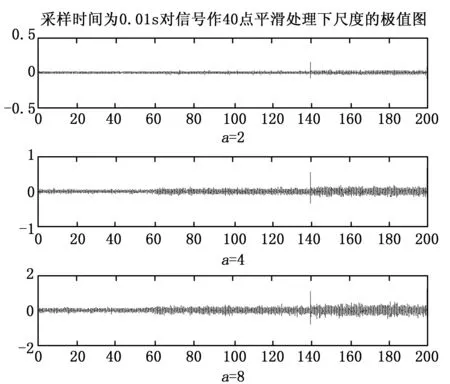
图6 平滑处理后各尺度极值图

图6的波形说明，平滑处理去除了大部分的干扰信号，使诊断结果更加清晰。这个仿真结果同时也证明连续小波变换方法诊断传感器故障不受输入信号突变的影响。

2.2 传感器输入信号均值恒为零时仿真研究

假设系统模型和各类信号不变，传感器输入信号u(t)的方差在t=60 s时刻从0.5变为2.0。取采样的时间为0.01 s，系统的输入输出信号如图7所示，同样利用db3小波基对其作连续小波变换，取采样时间为0.01 s，得到不同尺度下的极值如图8所示。

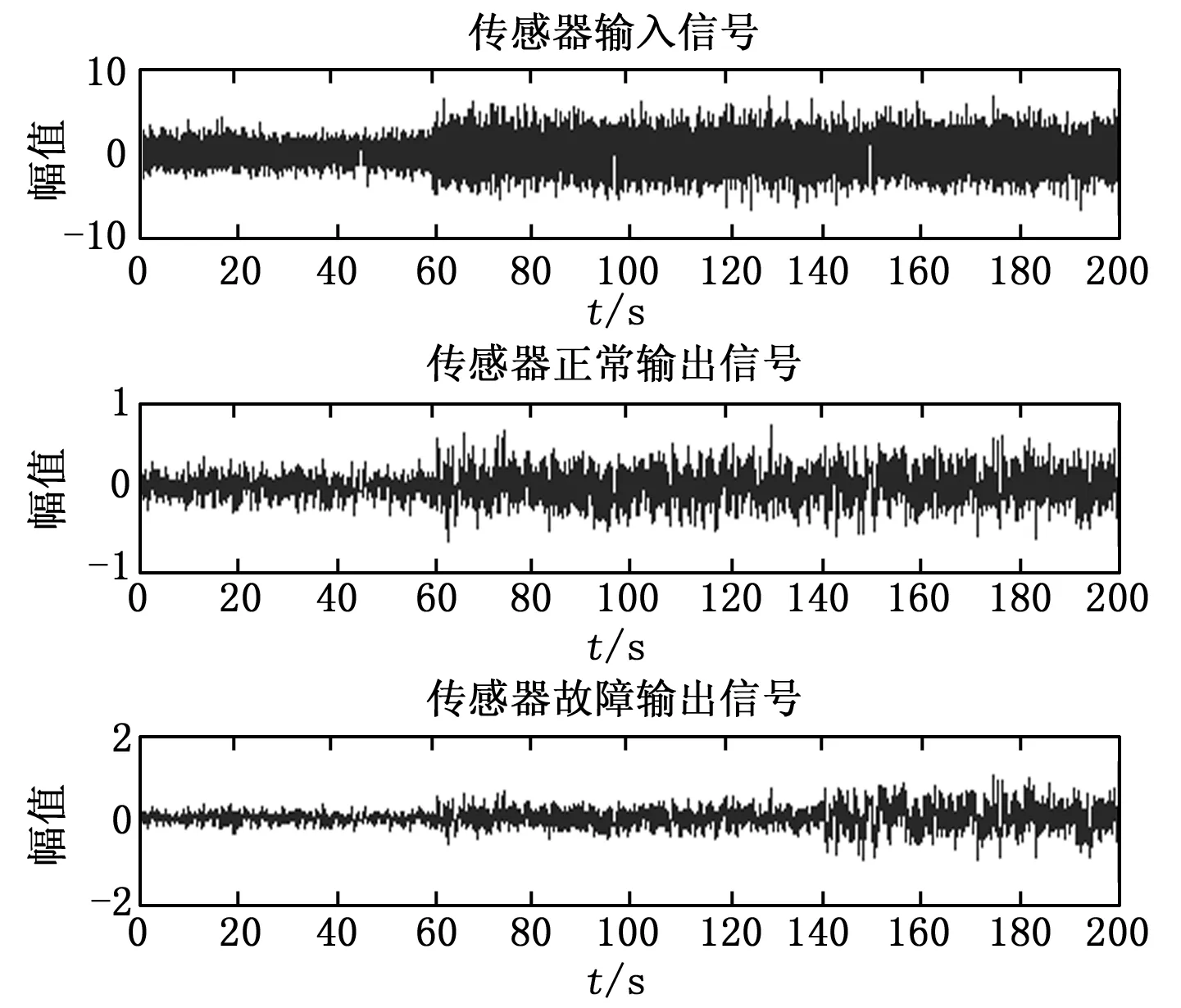
图7 传感器输入输出信号

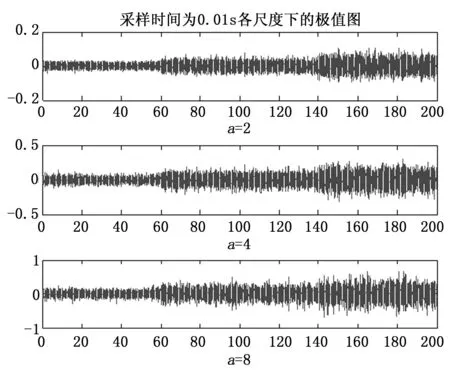
图8 各尺度极值图

从图8中的波形情况能够看出，各尺度下的极值图跳变点不明显，检测不出故障点。为此，我们经过反复实验发现对传感器输入输出信号做20点平滑消噪处理后，得到的极值图中能够将140 s时发生的传感器故障点检测出来，如图9为对信号作20点平滑处理的结果，图10为相应各尺度下的极值图。

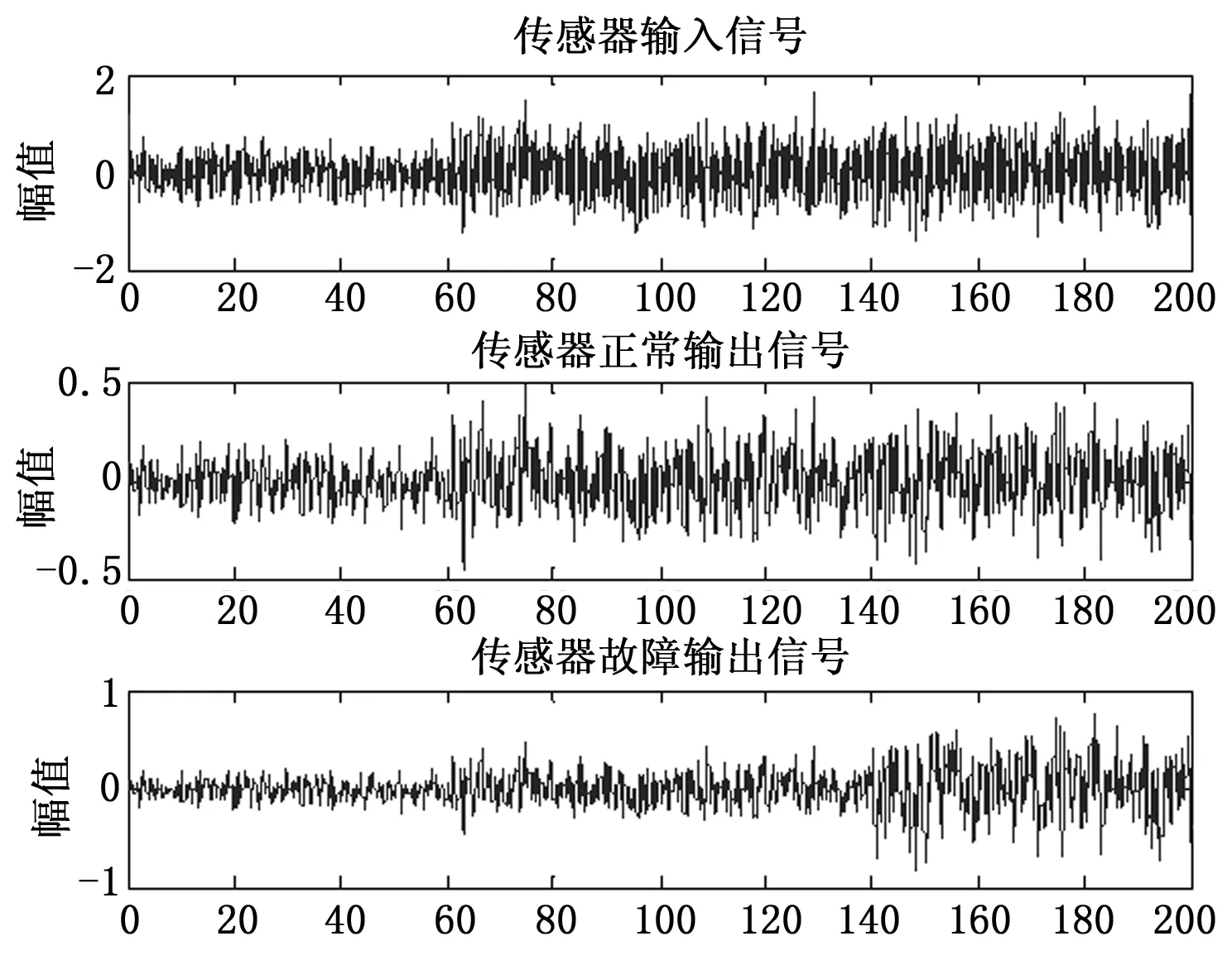
图9 对输入输出信号作20点平滑

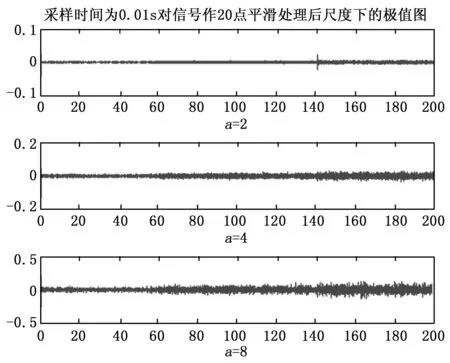
图10 各尺度下的极值图

观察图10可以看出，仅在尺度a=2的极值图中，t=140 s时刻有较明显的跳变出现，其他尺度的极值图中都没出现明显突变点。下面我们对a=2时的r(t)利用db3小波函数继续作连续小波变换，结果如图11所示。

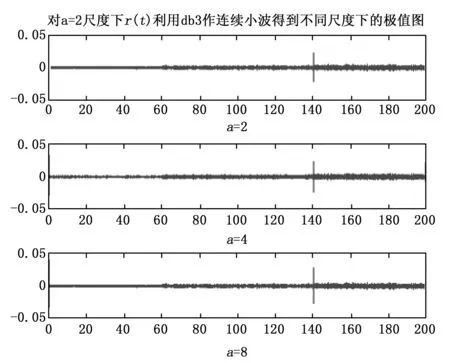
图11 对a=2尺度下的r(t)作连续小波变换的极值图

通过图11可以清晰看出，对r(t)再作连续小波变换，得到不同尺度下的极值图，t=140 s时都发生了明显的峰值。这就证明了该时刻传感器是有故障发生的。

通过以上的仿真实验结果来看，利用小波变换的方法能够在输入信号方差突变的情况下检测传感器故障并定位故障点，这也为下一步的故障分离和信号校正等处理做好了铺垫。

2.3 对常见传感器故障利用小波分析方法诊断实例

这里我们主要选取两种具有代表性的典型故障——偏置故障和开路故障进行仿真，进一步验证小波变换的方法能否诊断不同类型的传感器故障诊断。设正常运行时系统参数为:a=9,b=25,c=4,d=9，其他前提假设不变。根据传感器实际使用情况，本实验只考虑u(t)均值不为零的状态，因此将u(t)设置为分段平稳的均匀分布随机信号，它的均值在t=60sd的时刻从0.5突变成2，干扰信号e(t)采用高斯白噪声，其方差为0.1。

2.3.1 偏置故障

传感器偏置故障一般是由于传感器中偏置电流或偏置电压变化而导致的，为模拟偏置故障的发生[7]，本文采取在原传感器输出信号上加一个随机小信号的办法[7]。设置在时间t=140 s时在原传感器输出信号上加均值为1，方差为0.1的随机信号模拟偏置故障，取采样的时间为0.01 s，建立如图12所示的Simulink模型图，运行程序之后得到如图13所示的传感器输入输出信号。利用db3对输入输出信号作连续小波变换，得到各尺度下的极值如图14所示。

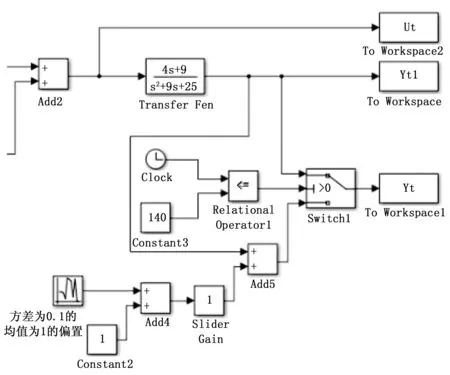
图12 偏置故障的传感器故障模型

图13 偏置故障下传感器输入输出信号

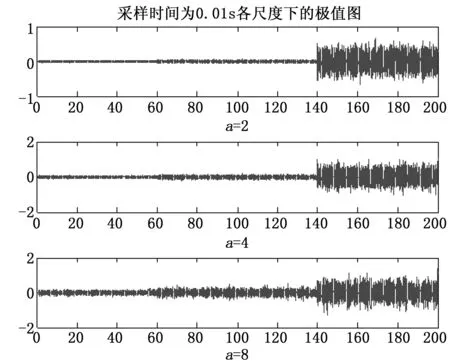
图14 偏置故障各尺度下的极值图

由图14看出，t=140 s时各极值图的波形出现了突变，但之后的干扰太大，从该图中检测不出发生偏置故障的位置。为了降低噪声干扰，对信号做10点的平滑处理，再利用db3对输入输出信号作连续小波变换，添加小波变换a=16尺度下的极值图，得到各尺度下的极值如图15所示。

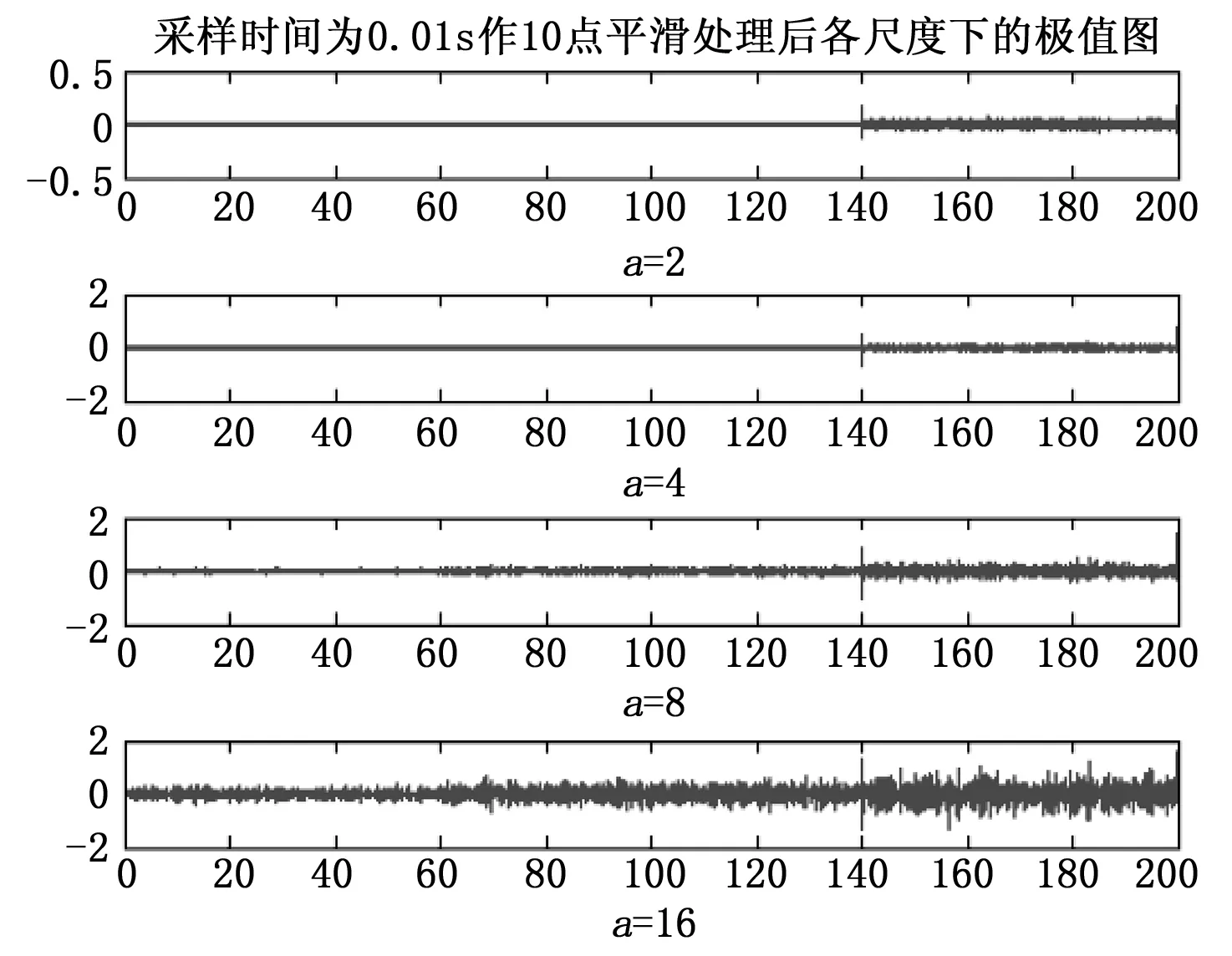
图15 偏置故障下各极值图

由图15的观察可以看出，传感器偏置故障发生的时刻能够在平滑处理后的各尺度极值图中很好的诊断出来。

2.3.2 开路故障

传感器的开路故障是由于信号线断、焊点脱焊等不可抗拒的物理原因造成的。在这里的仿真试验中为了模拟开路故障的发生，我们令传感器的信号在某一时刻突然接近输出的最大值。假设140 s时传感器发生开路故障，设其最大输出为恒定值8，采样时间取为0.01 s，得到传感器发生开路故障时的输入输出信号和各尺度下的极值如图16、17所示。

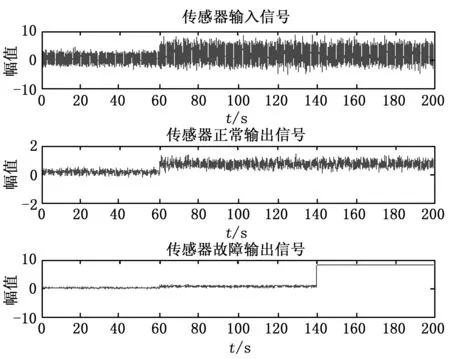
图16 开路故障输出输出图

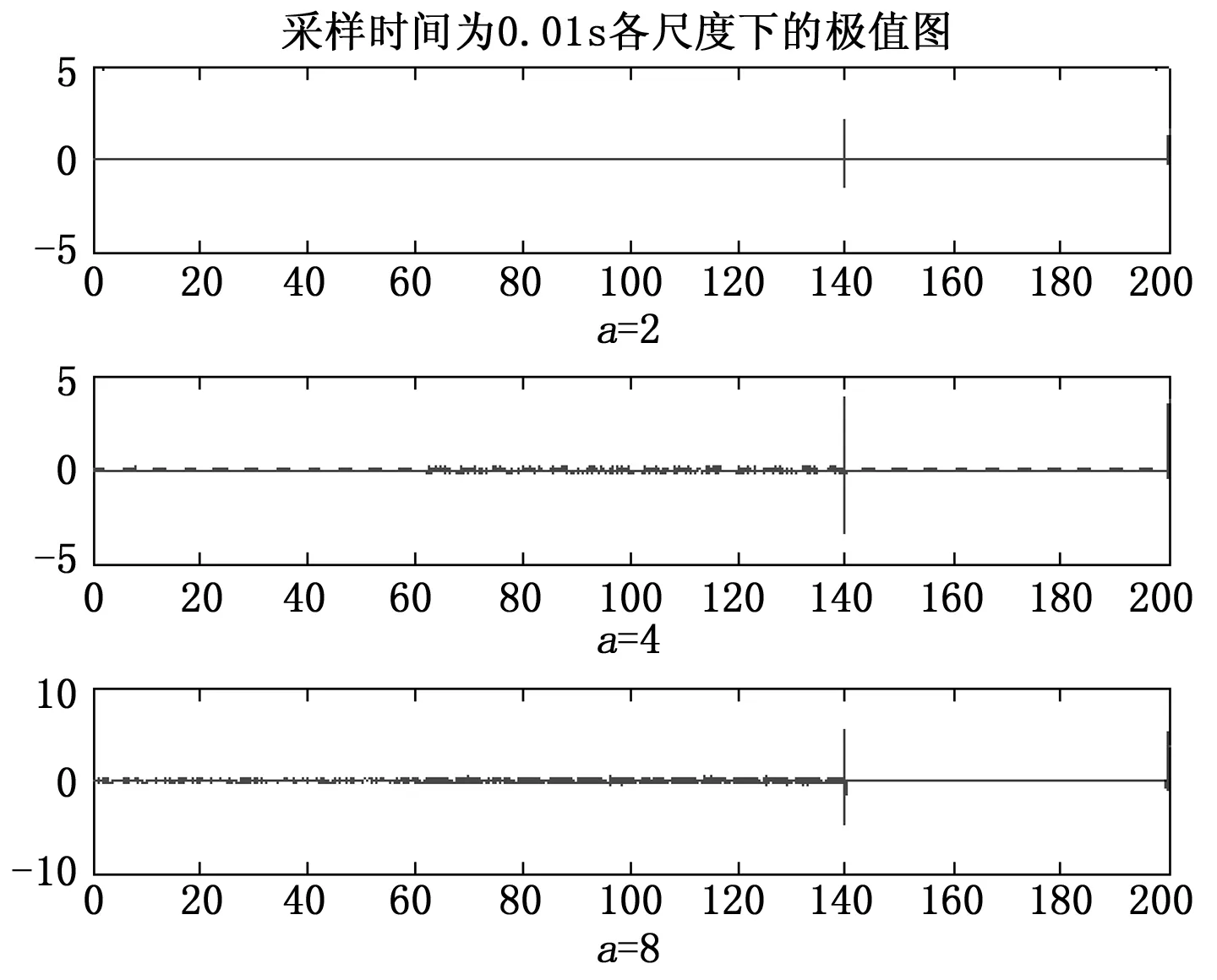
图17 开路故障各尺度极值图

图17的波形非常清晰，说明了利用连续小波变换的方法能够很好地检测出系统发生开路故障的时刻。

在这一节里我们选取的偏置故障和开路故障均是较为典型的常见传感器故障类型，通过仿真分析，对两种故障类型的诊断结果均较为理想。其余的传感器故障类型诊断方法和仿真建模思路大致相同，在此不再一一列出。

3 结论

本文主要研究了小波变换方法对传感器故障诊断的有效性，文章的第一部分先阐述了小波变换的基本理论，对连续小

波变换和离散小波变换的原理进行了介绍。第二部分接着利用Matlab/Simulink软件开展了仿真建模和程序编程的工作，验证了连续小波变换在传感器故障检测中的应用效果，从仿真得到的具体结果来看，仿真故障检测的效果良好。文章还按照传感器故障原因分类，依据计算机仿真实现方法对传感器偏置故障、开路故障在Matlab平台下进行了故障诊断的仿真，均得到了较好的效果。可以说，小波分析方法能够避免抽取对象的数学模型，适用性较强，不仅能诊断多数常见传感器故障类型，而且诊断故障的准确性较高。

参考文献：

[1] 王逍梦，任 章.基于小波变换的二阶传感器故障诊断研究[J].兵工自动化，2013(5)：74-78.

[2] 齐 涛，倪 原，徐 宁.基于小波变换的微弱生命信号去噪问题研究[J].生命科学仪器，2009(10)：20-23.

[3] 刘李鹂，高智勇，刘向明.基于小波变换的模极大值图像边缘检测算法[J].中南民族大学学报(自然科学版)，2006(4)：42-45.

[4] 吕纯洁，姚永玉，江 浩.历史时序数据相似性提取方法在机械故障诊断中的应用[J].机械研究与应用，2009(2)：21-23.

[5] 宋 新，刘次华，甄 新.奇异点检测的小波方法在信号初至时提取中的应用[J].湖北汽车工业学院学报，2001(2)：37-40.

[6] 黄治军.基于小波分析的传感器故障诊断研究[D].西安:西北工业大学，2004：31-53.

[7] 郑见阳.基于STF的飞控系统传感器故障诊断研究[D].沈阳:沈阳航空航天大学，2015：29-32.