海上低空突防群目标跟踪的IMM-Bayesian实现

王婷婷，缪礼锋，程 然

（中国航空工业集团公司雷华电子技术研究所，江苏无锡214063）

在现代对海战争中，群目标跟踪问题受到了国内外学者的广泛关注，尤其海上低空突防编队群目标具有检测率低、机动性强、战术性合并分裂等特征，在实战中灵活性更强、威胁性更大、对抗难度也更高。由于海上低空突防编队内的个体目标较为密集，海杂波干扰较为严重，受传感器分辨率的限制，完全分辨编队内个体目标较为困难[1]。在这种情况下，试图对群内所有个体分别进行跟踪变得不现实，这时可以将群目标看作一个整体进行跟踪[2]。在运动过程中，基于特定的突防战术或目的，海上低空突防编队群目标随时会发生转弯等整体机动，还会出现分裂、合并等编队群目标特有的机动模式，这种情况下，群内目标回波的相对位置发生缩放、旋转等变换[3-5]，导致群目标跟踪更为复杂。

基于群整体跟踪的思想，目前最经典的群跟踪的方法主要有两种：一类是Mahler在随机集框架下提出的概率密度假设（PHD）算法[6-8]，递推的传递目标状态的分布信息，不需要数据关联，即从目标状态分布中同时提取目标的个数和状态估计，但没有考虑群目标形状特征，也无法直接生成目标航迹，并且算法复杂，不利于实际工程应用。还有一类是KOCH等人提出的一种群目标Bayesian递推算法[9]，可以在跟踪群目标的质心状态同时，对群目标的形状进行估计。但是它目前仅用于跟踪无杂波条件下的单个群目标。随后，国内外学者又对这种算法进行了改进[10-16]，例如，Feldmann对群目标跟踪Bayesian算法进行了改进，考虑了量测不确定性对目标形状估计的影响。

本文在经典Bayesian算法的基础上，针对海上低空突防编队群目标的3种典型机动模式（拐弯、分裂、合并），将交互式多模型（Interacting Multiple Model，IMM）算法与群目标Bayesian递推算法相结合，并利用随机矩阵描述群目标的形状扩展状态，采用IMMBayesian算法对机动群目标进行有效跟踪的同时，用椭圆拟合群目标的形状。

1 群目标模型

将海上低空突防群目标看作一个整体，假设在tk时刻群质心的运动状态向量为，包括了位置、速度、加速度等空间维数。表示tk时刻目标的位置表示tk时刻目标的速度表示tk时刻目标的加速度。Bayesian递推算法用表示群质心的运动状态向量，并增加了一个正定随机矩阵Xk来描述该群的形状特征，该方法将目标的形状用一个椭圆来近似，椭圆方程可以用二次型方程表示为：

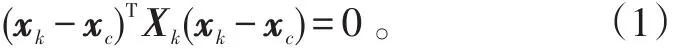
式（1）中：xc为椭圆中心；正定矩阵Xk的特征值为椭圆各轴的长度，其所对应的特征向量为其椭圆各轴的方向向量。

该方法的性质完备地描述了空间或平面内一个椭圆的全部信息。

用状态(xk,Xk)描述tk时刻群目标的状态，依据经典Kalman滤波理论，对群目标质心建立如下动力学方程：

式（2）中：Fk为状态转移矩阵；wk为过程噪声，是零均值的高斯白噪声，即wk～N(0,Δk|k-1)。

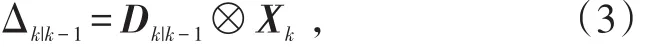
式中：⊗为kronecker积，采用Van Keuk模型[17]；

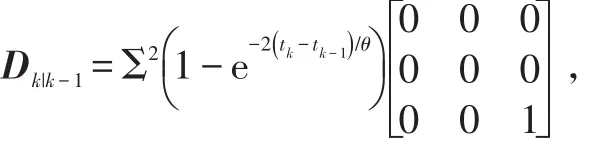
其中，θ为机动飞行相关的时间常数。

群目标量测模型为：

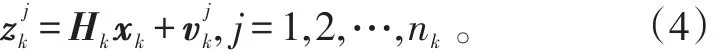
式（4）中：Hk为量测矩阵；vkj为量测噪声，是零均值的高斯白噪声，vk～N(0 ,λXk+Rk)，其中，λ为标量，用于描述Xk对量测的影响程度，Rk为量测噪声协方差；nk为tk时刻某群目标得到的量测个数。

2 群目标跟踪的Bayesian方法

2.1 群目标跟踪预测部分

利用先前的信息，对被跟踪目标的下一时刻的信息进行估计，即

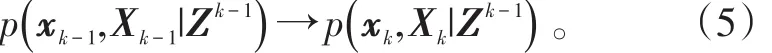
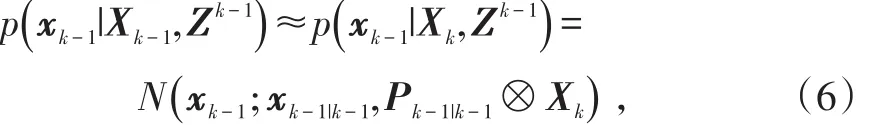
式中，Pk-1|k-1为tk-1时刻状态估计误差协方差。

那么，一步预测：

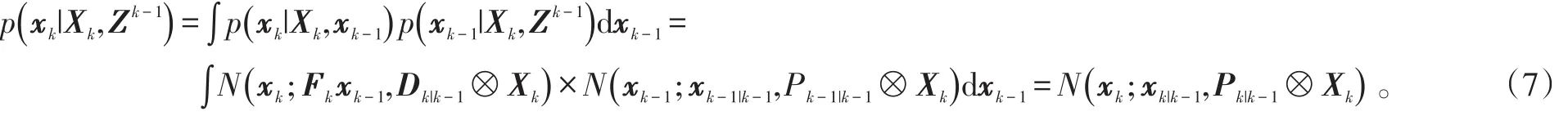
所以，目标的运动状态预测为：

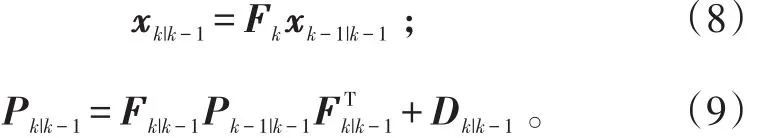
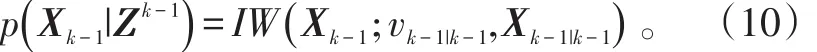
式（10）中存在一个未被限制的参量vk-1|k-1，由逆Wishart分布相关知识可知，此参量与Xk-1有关，它在每一时刻的取值必须在实际跟踪中进行合理的设定或递归处理。通常设定vk-1|k-1和Xk-1|k-1与上一次预测后的值相关。p(Xk|Zk-1)同样满足逆Wishart分布，并有形式：

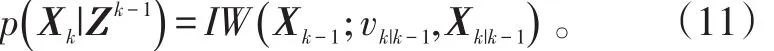
考虑一个关于vk-1|k-1和vk|k-1的衰减模型，这种衰减也与采样区间T相关，即

存在未被限定的参量τ作为衰减因子常量，需要在实际跟踪中进行合理的设定。当τ=∞时，代表群目标的形状不发生变化。

假设预测步前后Xk-1和Xk的期望值相等。由逆Wishart分布的知识，有：

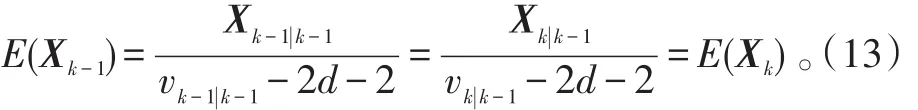
式（13）中，d为矩阵X的维数。

那么，形状扩展状态的预测为：

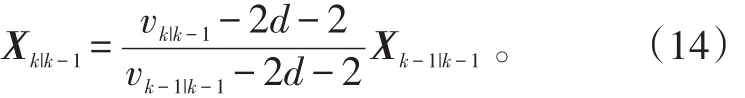
2.2 群目标跟踪更新部分

对被跟踪目标的相关信息的更新，即

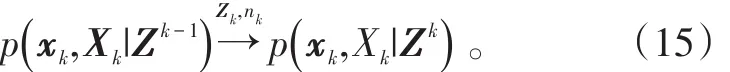
引入似然函数：

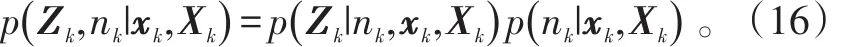
式（16）中，nk为当前时刻的群目标的量测个数，其与当前的动力学状态和形状状态无关。

p(nk|xk,Xk)可以看作一个常数，并且

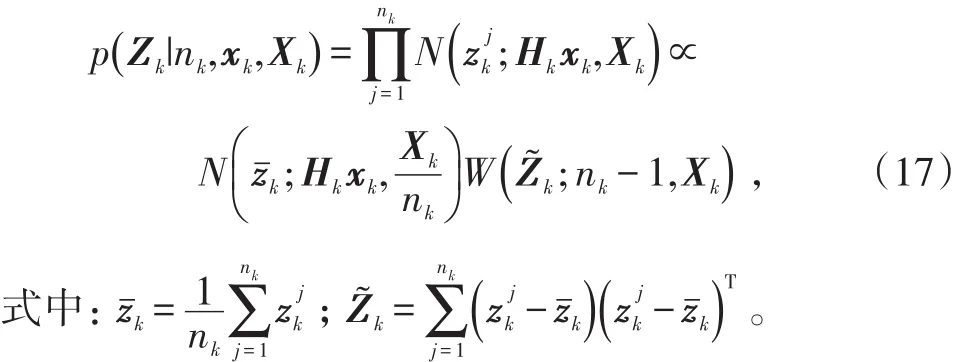
利用预测部分得到的结果，由Bayesian先验概率公式，可得：

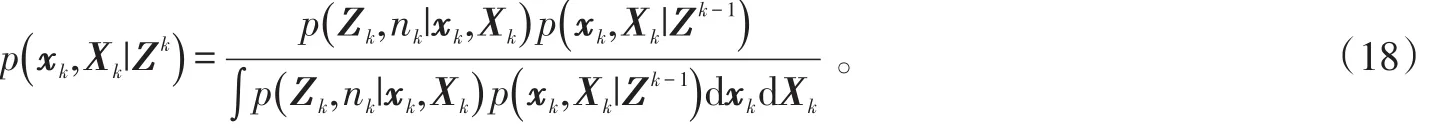
所以：

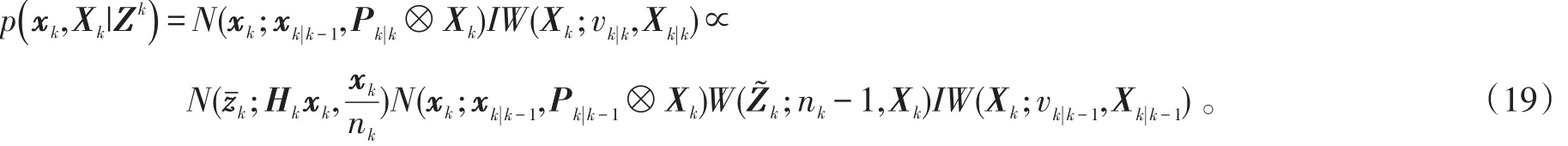
目标的运动状态更新为：

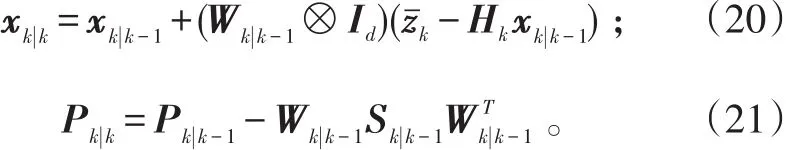
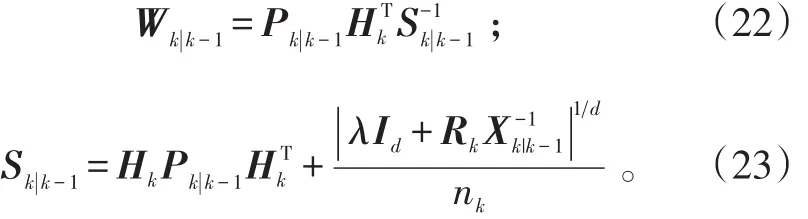
式（20）、（21）中：

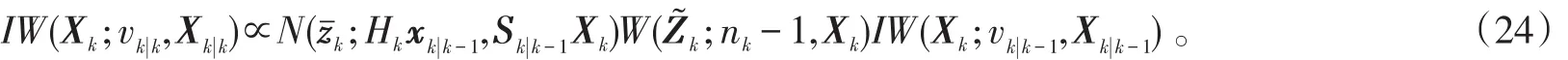
式（24）中：

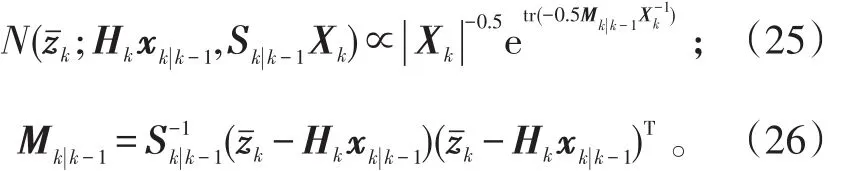
所以，

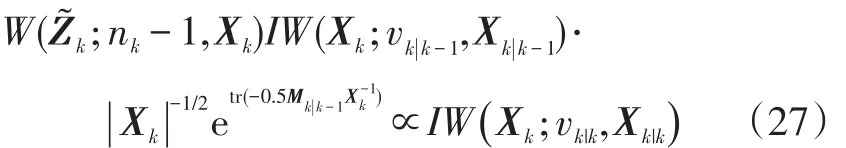
目标形状扩展的更新为：

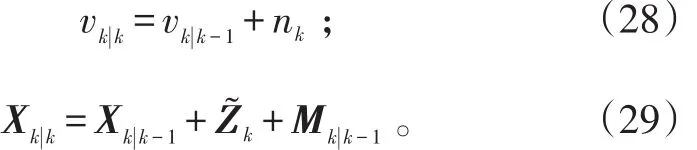
至此，对于被跟踪的群目标的一个可用的跟踪算法已被建立起来。

3 IMM-Bayesian算法

在广义Bayesian算法的基础上，采用具有Markov切换系数的IMM算法，推导了IMM-Bayesian算法对海上低空突防编队群目标进行跟踪。在tk时刻，利用IMM进行目标状态估计的计算时，考虑每个模型滤波对于目标的扩展部分，器都有可能成为当前有效地系统模型滤波器，每个滤波器的初始条件都是基于前一时刻各条件模型滤波结果的合成。IMM-Bayesian算法对海上低空突防编队群目标跟踪的具体递推步骤如下：

1）模型条件初始化。模型条件重初始化是在假定第j个模型在当前时刻有效的条件下，与其匹配的滤波器的输入由上一时刻各滤波器的估计混合而成。

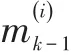
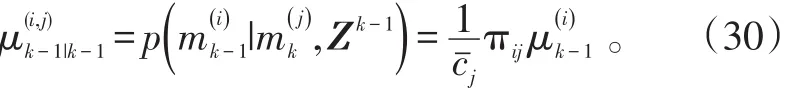
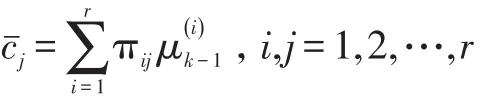
对于j=1,2,…,r，重初始化的运动状态、形状扩展状态与协方差阵按混合估计分别为：

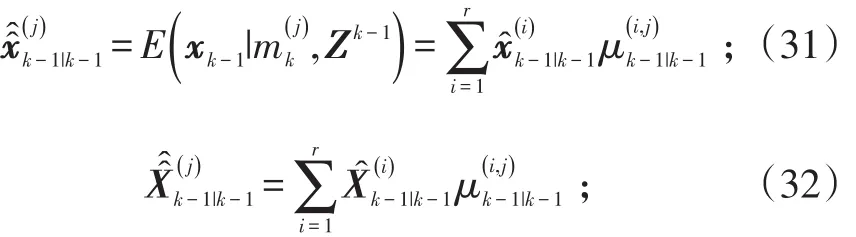
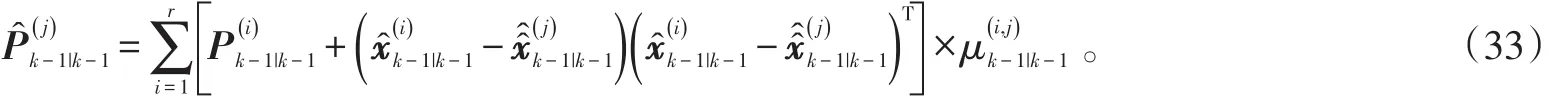
2）模型条件滤波。模型条件滤波是在给定重初始化的状态和协方差阵的前提下，在获得新的量测zk之后，进行状态估计更新。

对于j=1,2,…,r，状态预测为：

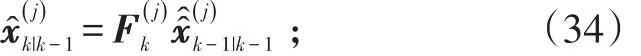
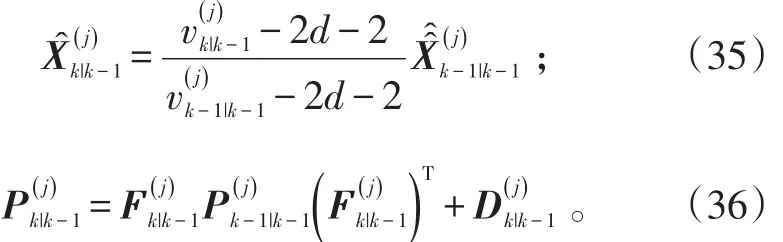
对于j=1,2,…,r，分别计算量测预测残差与其协方差阵：

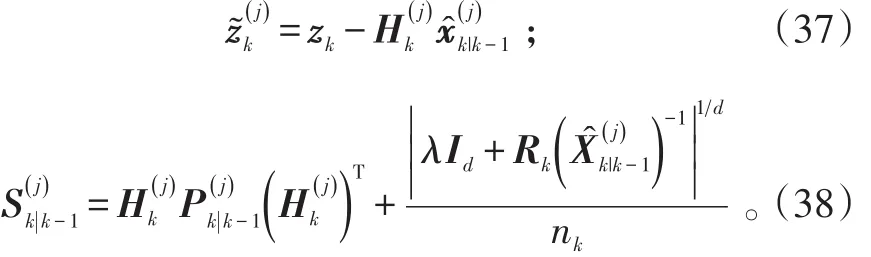
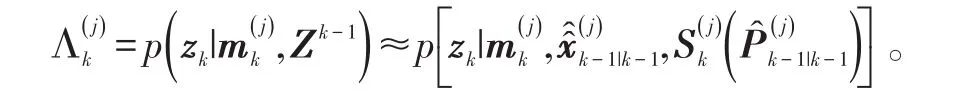
在Gaussian假设下，似然函数可以计算如下：

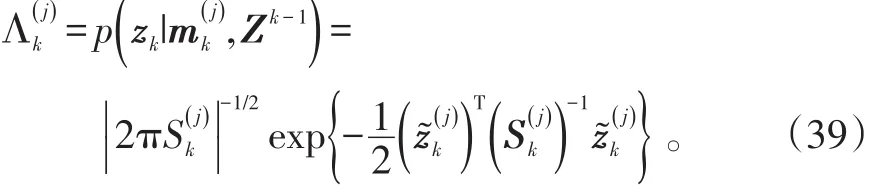
滤波增益阵、状态估计更新、形状扩展状态更新和状态估计更新误差协方差阵如下：

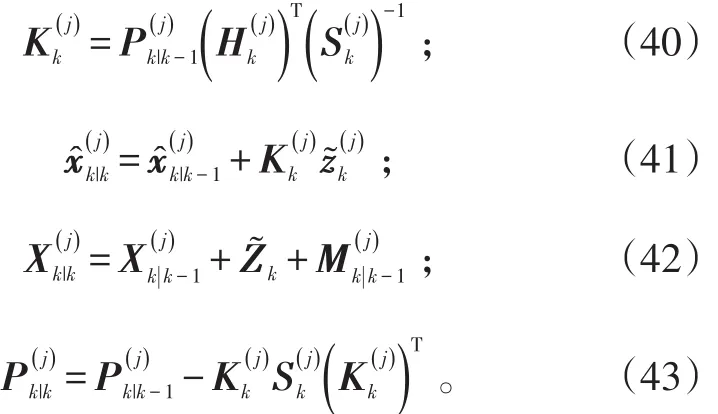
式（42）中：

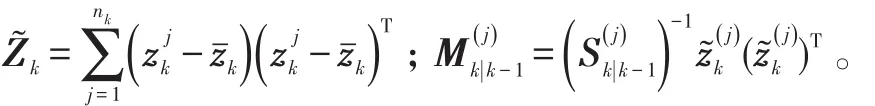
3）模型概率更新。对j=1,2,…,r，计算模型概率：

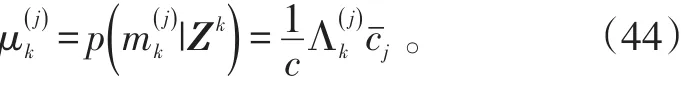
4）输出交互。给出运动状态估计、形状扩展状态估计和误差协方差阵，分别为：

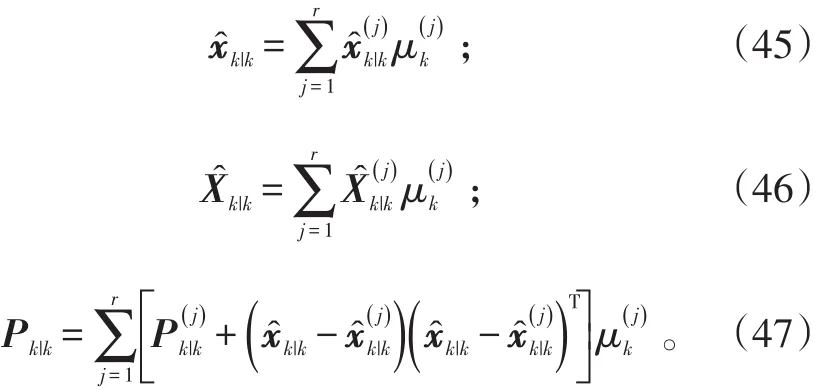
4 转弯模式下群目标跟踪实现

假设海上低空突防群目标的质心按图1轨迹匀速运动，速度为 300 m/s，在采样区间k=13～15、k=25～29、k=39～44进行机动转弯，分别转过 45°、90°和90°，其他时间段均为300 m/s的匀速运动。量测噪声服从分布，其中α=1/4。将表征机动群目标形状特征的正定对称矩阵初始化为X=diag([ 2 000,2000])，Rk=diag([ 25,25])。在每次扫描过程中，量测数据的个数服从均值为λ=12的泊松分布。群目标形状更新时间延迟参数τ=8T。

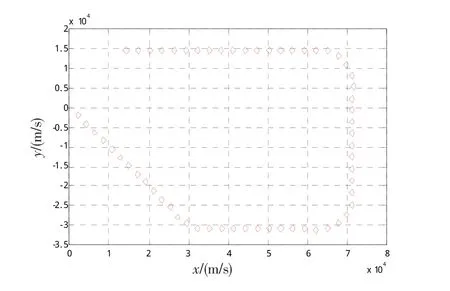
图1 群目标运动轨迹Fig.1 Trajectory of group target

对于给定的场景，采用3个模型。第1个模型为CV模型；第2个模型为CT模型，ω1=-0.01πrad/s；第3个模型为CT模型，ω2=-0.0125πrad/s。则群目标跟踪结果、模型匹配结果以及跟踪误差如图2～4所示。

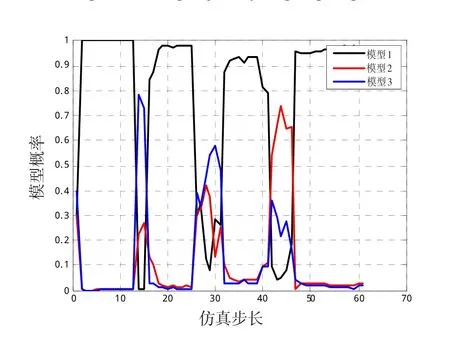
图3 模型概率Fig.3 Model probability

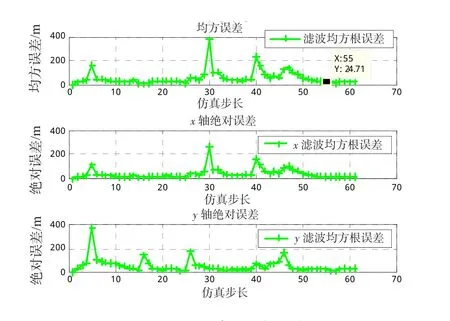
图4 群目标跟踪误差Fig.4 Tracking error of group target

通过仿真可看出，采用IMM-Bayesian方法对在海上低空突防编队群目标转弯的情况下可以达到较好的跟踪效果，图3给出了不同采样时刻的模型匹配结果，可以看出选用的3个模型可以较好地完成模型匹配，模型匹配与真实运动过程模型基本吻合。从图4可以看出，分别采用多模型进行群目标跟踪平均误差较小，跟踪精度较高，但在目标机动位置误差会增大。

5 群目标的分裂与合并实现

针对海战场探测区域中出现的低空突防群目标进行分裂或合并的情况，根据最近邻的思想，将得到的量测进行分类，再根据群目标的跟踪算法对其实施有效跟踪。在第k个扫描周期，采用分类器将得到的所有量测进行分类，分类个数记作nClass(k)。与前一时刻的nClass(k-1)比较。若nClass(k)=nClass(k-1)，则说明检测到的群目标没有进行分裂或合并，先采用关联算法进行k与k-1时刻各分群的关联，关联之后分别进行跟踪；若nClass(k)≠nClass(k-1)，则说明检测到的群目标进行了分裂（满足nClass(k)＞nClass(k-1)）或合并（满足nClass(k)＜nClass(k-1)），则需对k时刻的各个分群分别进行初始化。

群目标分离场景设置：假设海上低空突防编队群目标质心初始位置[0,0]，开始以300 m/s的速度沿45°方向运动。t=39T时，群目标中部分目标出现分离，形成分群1和分群2。分群1始终保持匀速直线运动，分群2以(1 . 873×2π/360) rad/s的角速度匀速向右偏转，当t＞64T后，分离出来的目标2机动停止，保持匀速直线运动。

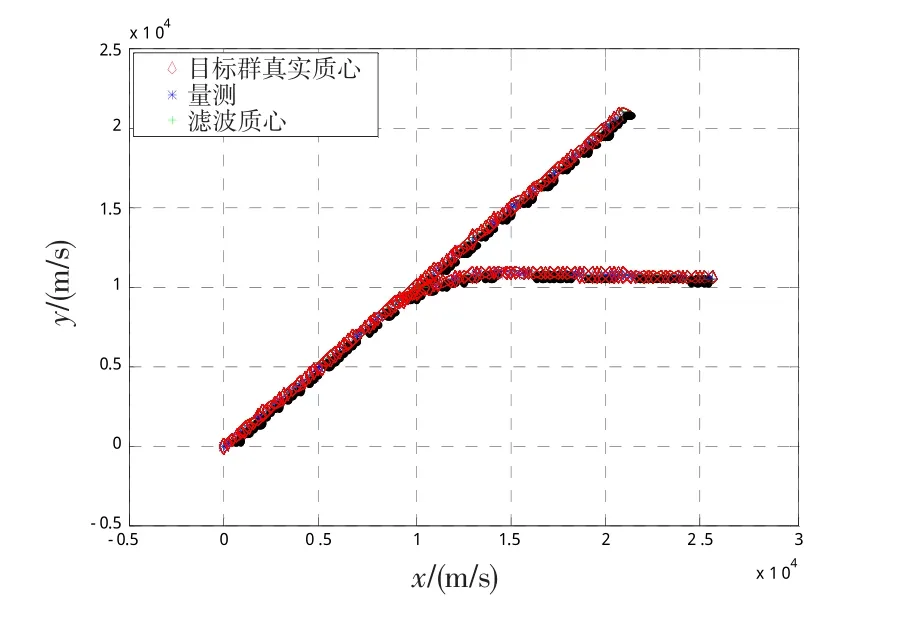
图5 群目标分离Fig.5 Splitting trajectory of group target

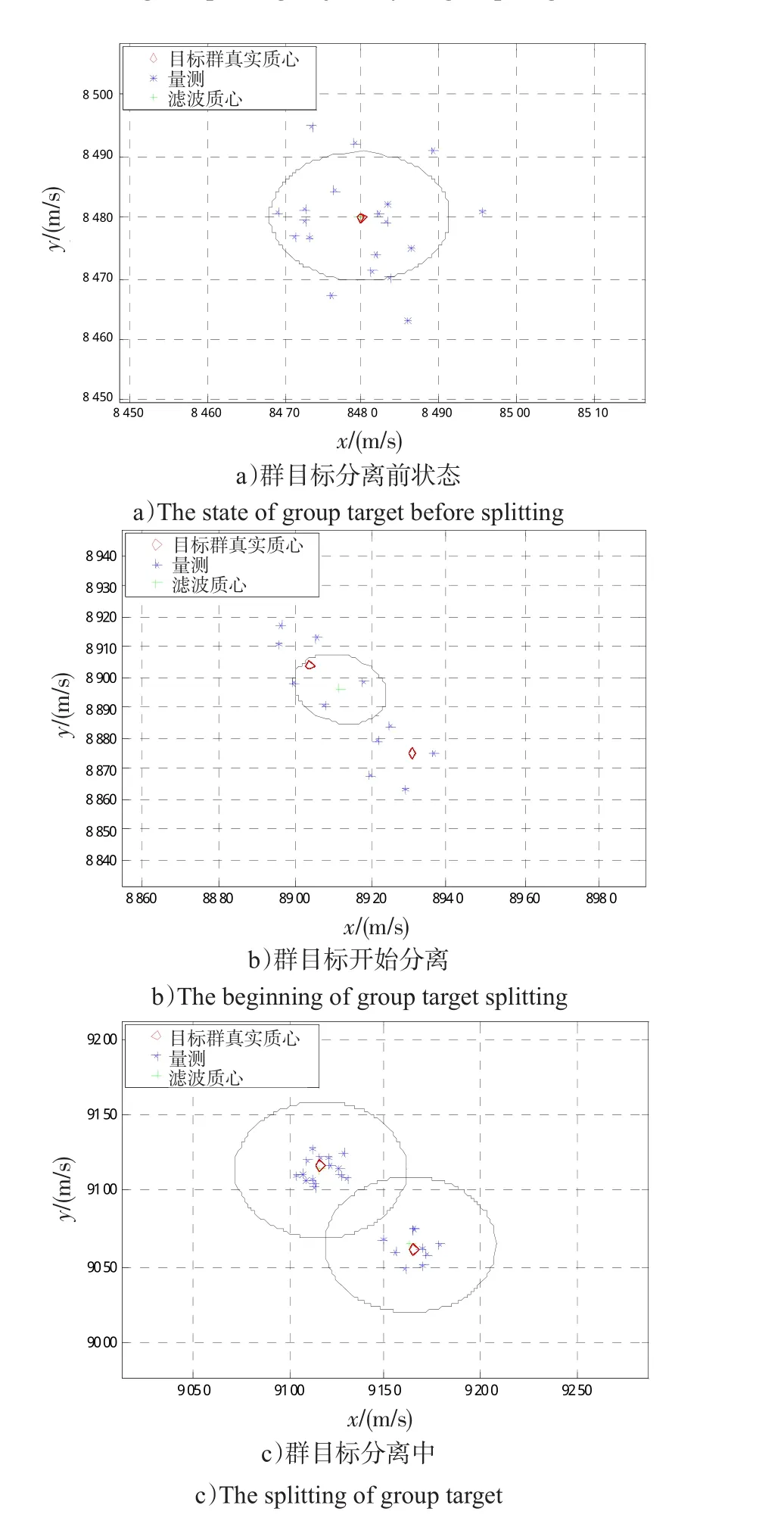
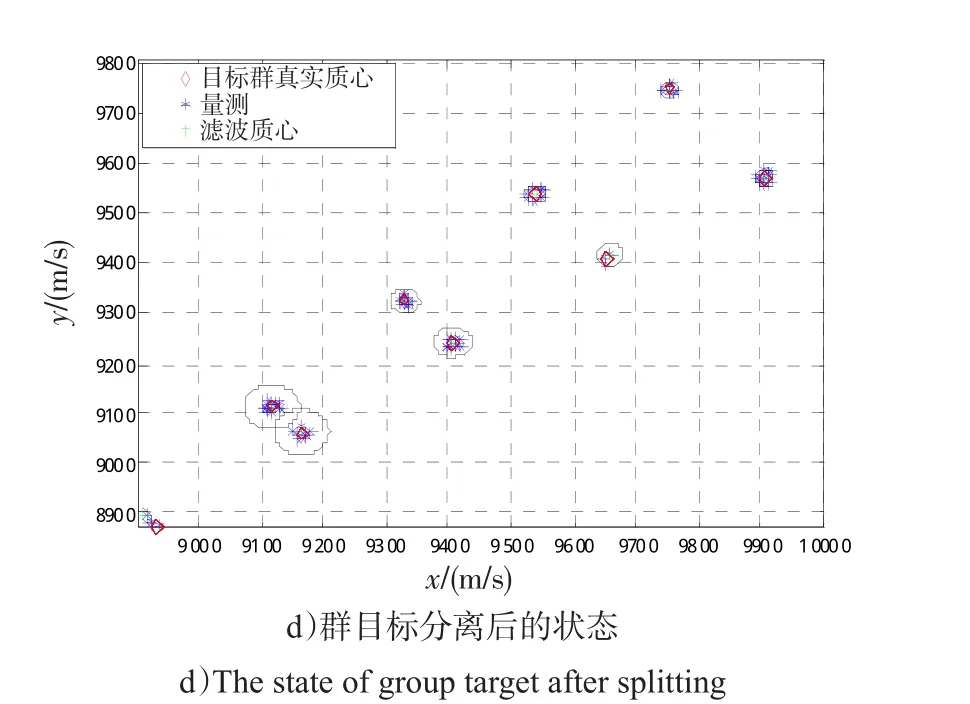
图6 群目标分离过程Fig.6 Splitting process of group target

仿真可以看出，IMM-Bayesian算法可在海上低空突防编队群目标分裂时进行稳定跟踪，随机矩阵可对群目标形状进行拟合，图6清晰地展现了群目标分裂过程中目标的跟踪情况，当出现2个椭圆时，说明群目标已完成分裂，之后当成2个群目标进行稳定跟踪。

群目标合并场景设置：假设检测到海上有2个分群目标，分群1初始位置为[0,3488]，分群2初始位置为[0,0]，开始均以300 m/s的速度沿x轴方向运动。t=39T时，分群1和分群2开始机动，在39T＜t＜54T时间段，分群1以(1 .5×2π/360) rad/s的角速度匀速向右偏转；分群2以(- 1.5×2π/360) rad/s的角速度匀速向左偏转。在 54T＜t＜69T时间段，分群1以(-1.5×2π/360) rad/s的角速度匀速向左偏转；分群2以(1 . 5×2π/360) rad/s的角速度匀速向右偏转。之后，分群1和分群2机动停止，保持匀速直线运动。

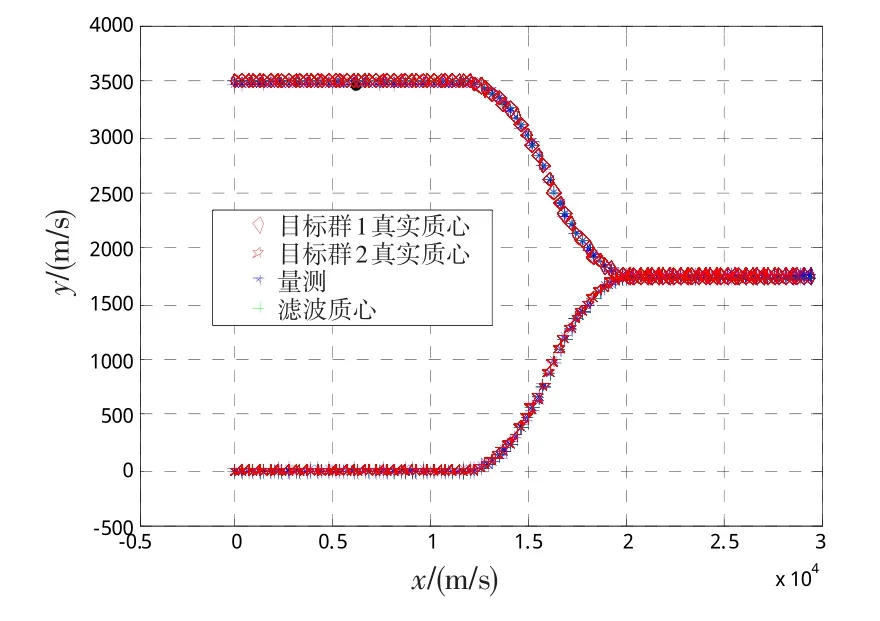
图7 群目标合并轨迹Fig.7 Merging trajectory of group target

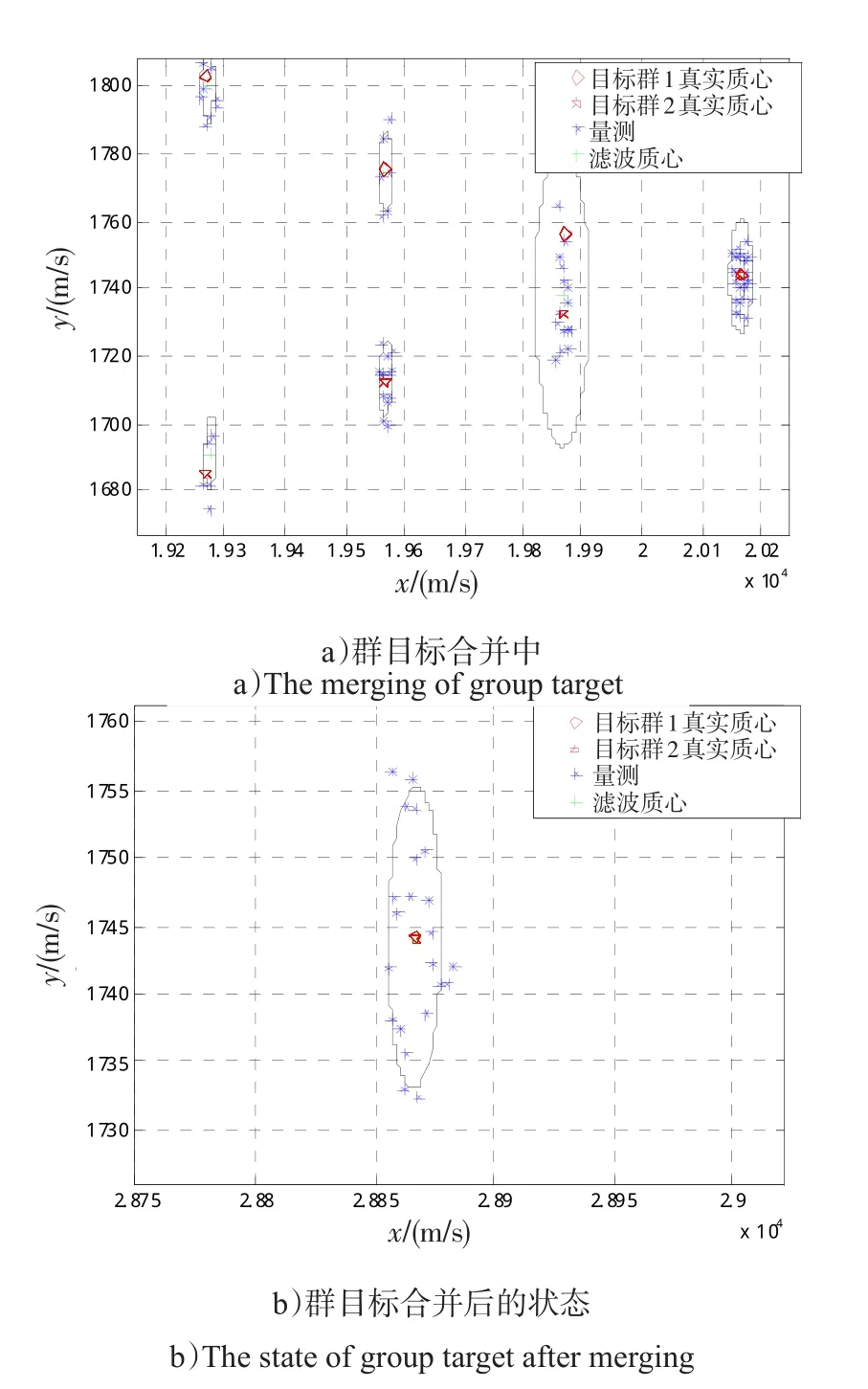
图8 群目标合并过程Fig.8 Merging process of group target

仿真可以看出，IMM-Bayesian算法可在海上低空突防编队群目标合并时进行稳定跟踪，随机矩阵可实施估计群目标形状，图8展现了群目标合并过程中目标的跟踪情况，当2个椭圆合并成1个椭圆时，说明群目标已完成合并，之后当成1个群目标进行稳定跟踪。

6 结论

针对拐弯、分裂、合并等典型海上低空突防编队群目标机动模式，将IMM算法与Bayesian递推算法结合，完成对海上低空突防群目标整体的跟踪，并利用随机矩阵描述群目标形状特征，采用椭圆拟合群目标形状。其中针对群目标出现的分裂合并现象，采用基于最近邻算法思想的跟踪算法对群目标进行稳定跟踪。本算法只针对单个传感器对海上群目标的跟踪，又由于用椭圆仅是粗略地对群目标形状进行估计，需进一步研究使其能更加精确的估计群目标的形状。

参考文献：

[1]连峰，王婷婷，韩崇昭.多个不可分辨目标群的联合检测与估计误差界[J].西安交通大学学报，2015，49（11）：89-95.LIAN FENG，WANG TINGTING，HAN CHONGZHAO.Error bounds of joint detection and estimation for multiple unresolved target-groups[J].Journal of Xi’an Jiaotong University，2015，49（11）：89-95.（in Chinese）

[2]耿文东.基于群目标几何中心的群起始算法研究[J].系统工程与电子技术，2008，30（2）：269-272.GENG WENDONG.Study of group-initialization method based on group-target center of geometry[J].Systems Engineering and Eletronics，2008，30（2）：269-272.（in Chinese）

[3]王海鹏，唐田田，王子玲，等.面向群目标典型机动的多传感器精细跟踪方法[J].船舶电子工程，2016，36（8）：76-80.WANG HAIPENG，TANG TIANTIAN，WANG ZILING，et al.Multi-sensor refined tracking algorithm of typical group targets maneuvering models[J].Ship Electronic Engineering，2016，36（8）：76-80.（in Chinese）

[4]耿文东，王元钦，董正宏.群目标跟踪[M].北京：国防工业出版社，2014：100-122.GENG WENDONG，WANG YUANQIN，DONG ZHENGHONG.Group-target tracking[M].Beijing：National Defense Industry Press，2014：100-122.（in Chinese）

[5]耿文东.基于PDA的群目标合并与分离方法研究[J].无线电工程，2007，37（2）：24-30.GENG WENDONG.A study on group target merging and splitting method based on PDA[J].Radio Engineering，2007，37（2）：24-30.（in Chinese）

[6]MAHLER R.Multi-target Bayes filtering via first-order multi-target moments[J].IEEE Transactions on Aerospace and Electronic Systems，2003，39（4）：1152-1178.

[7]MAHLER R.PHD filters of higher order in target number[J].IEEE Transactions on Aerospace and Electronic Systems，2007，43（4）：1523-1543.

[8]张慧，徐晖，王雪莹，等.一种基于椭圆随机超曲面模型的群目标高斯混合PHD滤波器[J].光学学报，2013，33（9）：1-10.ZHANG HUI，XU HUI，WANG XUEYING，et al.A Gaussion mixture PHD filter for group targets tracking based on ellipse random hypersurface models[J].Acta Optica Sinica，2013，33（9）：1-10.（in Chinese）

[9]KOCH W.Bayesian approach to extended object and cluster tracking using random matrices[J].IEEE Transactions on Aerospace and Electronic Systems，2008，44（3）：1042-1059.

[10]FELDMANN M，FRÄNKEN D.Tracking of extended objects and group targets using random matrices—a new approach[C]//Proceedings of the 11thInternational Conference on Information Fusion.Cologne：IEEE，2008：1-8.

[11]FELDMANN M，FRÄNKEN D，KOCH W.Tracking of extended objects and group targets using random matrices[J].IEEE Transactions on Signal Processing，2011，59（4）：1409-1420.

[12]FELDMANN M，FRANKEN D.Advances on tracking of extended objects and group targets using random matrices[C]//Proceedings of the 12thInternational Conference on Information Fusion.Seattle，Washington，USA：IEEE，2009：1029-1036.

[13]韩玉兰，朱洪艳，韩崇昭.采用随机矩阵的多扩展目标滤波器[J].西安交通大学学报，2015，49（7）：98-104.HAN YULAN，ZHU HONGYAN，HAN CHONGZHAO.A multi-target filter based on random matrix[J].Journal of Xi’an Jiaotong University，2015，49（7）：98-104.（in Chinese）

[14]WIENEKE M，KOCH W.Probabilistic tracking of multiple extended targets using random matrices[C]//Proceedings of SPIE.2010，7698：1-12.

[15]BAUM M，NOACK B，HANEBECK U D.Mixture random hypersurface models for tracking multiple extended objects[C]//Proceedings of the IEEE Conference on Decision and Control.Piscataway，NJ，USA：IEEE，2011：3166-3171.

[16]王婷婷，何科峰，程然.具有形状信息的多个群目标跟踪算法[J].雷达科学与技术，2017，15（5）：531-536.WANG TINGTING，HE KEFENG，CHENG RAN.A tracking algorithm for multiple group-targets with shape information[J].Radar Science and Technology，2017，15（5）：531-536.（in Chinese）

[17]VAN KEUK G，BLACKMAN S S.On phased-array radar tracking and parameter control[J].IEEE Transactions on Aerospace&Electronic Systems Aes，1993，29（1）：186-194.

[18]HAFF L R.Identities for the inverse Wishart distribution with computational results in linear and quadratic discrimination[J].The Indian Journal of Statistics：Series B，1982，44（3）：245-258.