这样的错误，你有过吗？——一类漏解问题的剖析

唐华金

在平时学习过程中，我们或多或少会犯一些令人后悔的错误，有的是因为思维上的漏洞，也有的是因为“粗心”，很多同学考试过后都很自责.怎样减少甚至杜绝那些令人惋惜的错误的发生？老师建议大家首先要找出错误的背后原因，努力从自身内部增强“免疫力”，提高战斗力！下面通过几道典型例题进行分析，希望大家对照之后认真反思.

例1 已知△ABC∽△DEF，若△ABC的边长分别为5cm，6cm，7cm，而4cm是△DEF中一边的长度，则△DEF的另外两边的长度是________.

【典型错例】考虑到△ABC∽△DEF，所以其三边对应成比例，设△DEF的另外两边的长分别为x、y，则，解之得

【错因分析】看到条件“4cm是△DEF中一边的长度”，自问一下，它是哪一条边的长度？仔细一想，4cm的这条边可能是△DEF三条边中的任意一条，所以无法确定它与谁对应，需要分情况讨论.①当4cm与5cm对应时；②当4cm与6cm对应时解得：；③当4cm与7cm对应时解得综上所述：另外两边的长度是老师提醒大家：“当题目中的某个条件没有确定时，一定要注意分类讨论.”

例2 如图1，M是Rt△ABC的斜边BC上异于B、C的一定点，过M作直线截△ABC，使截得的三角形与△ABC相似，这样的直线共有（ ）.

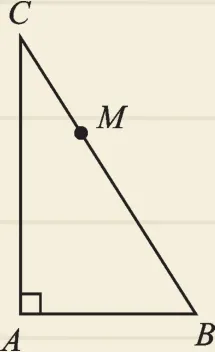
图1

A.4条 B.3条 C.2条 D.1条

【典型错例】由于△ABC是直角三角形，所以截得的三角形应该也是直角三角形.如图2，考虑到两直线平行，同位角相等，所以过点M分别作AB、AC的平行线，交AC、AB于点D、E，则截得的△DMC、△EBM均与△ABC相似.

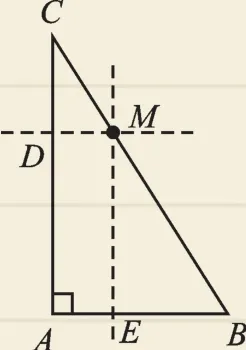
图2

【错因分析】如图3，若过点M作FM⊥BC，交AC于F，则截得的△CFM也与△ABC相似.很多同学只考虑了平行截取，没有考虑到这种情况.事实上，只要过点M作直线与另一边相交，所截得的三角形与原三角形一定有一个公共角，再作出一个直角就可以了.在分类思想的指引下，过点M分别作三边的垂线即可截得，所以这样的直线共有3条.老师提醒大家：“找与已知三角形相似的三角形要能抓住关键的角.”

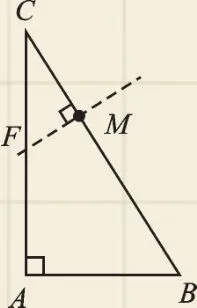
图3

例3 如图4，在平面直角坐标系中，△ABC的顶点坐标分别为A（4，0）、B（8，2）、C（6，4），已知△A1B1C1的两个顶点坐标分别为（1，3）、（2，5），若△ABC与△A1B1C1位似，则△A1B1C1的第三个顶点的坐标为____.

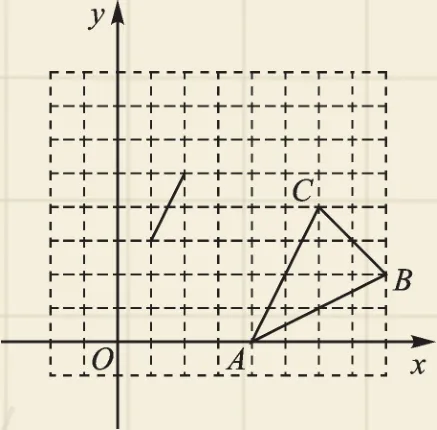
图4

【典型错例】如图5，将点A和坐标为（1，3）的点作为对应点，点C和坐标为（2，5）的点作为对应点，并分别以两组对应点作直线，确定其交点（-2，6）为位似中心，并求得△ABC与△A1B1C1的相似比为2∶1，连接DB即可确定第三个顶点的坐标为（3，4）.

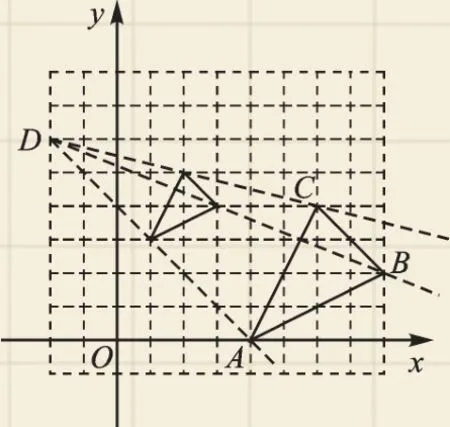
图5

【错因分析】只考虑了位似中心在两个三角形同侧的情况，而未考虑位似中心在两个三角形之间的情况.如图6，当位似中心在两三角形之间时，将点A和坐标为（2，5）的点作为对应点，点C和坐标为（1，3）的点作为对应点，并分别以两组对应点作直线，确定其交点为位似中心，并求得△ABC与△A1B1C1的位似比仍为2∶1，同样的方法求得△A1B1C1的第三个顶点的坐标为（0，4）（也可结合一次函数的相关知识求解），所以第三个顶点的坐标为（3，4）或（0，4）.老师提醒大家：“遇到位似问题一定要考虑位似中心的位置，看是否有两种情况.”

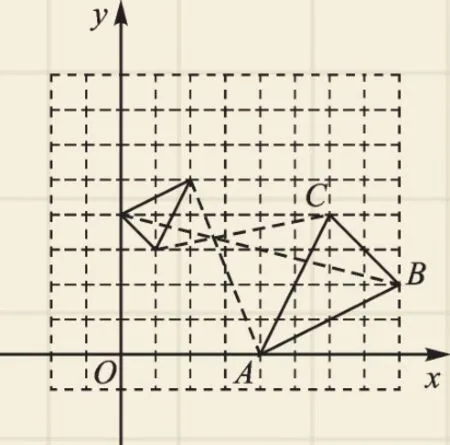
图6

例4 在△ABC中，AD是边BC上的高，AD=2，DB=2，CD=23，求∠BAC的度数.

【典型错例】如图7，△ABC的高AD将其分成两个特殊的三角形：等腰直角三角形ADB和含30°的直角三角形 ACD，∠BAC=∠BAD+∠CAD=105°.

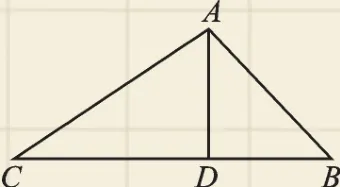
图7

【错因分析】错例中只考虑了三角形的高在其内部时的情况，未考虑三角形的高在其外部时的情况，导致漏解.如图8，当△ABC的高AD在其外部时（垂足落在CB延长线上），∠BAC=∠CAD-∠BAD=60°-45°=15°，所以∠BAC的度数为 105°或 15°.老师提醒大家：“题目无图要当心，都是无图惹的祸！”

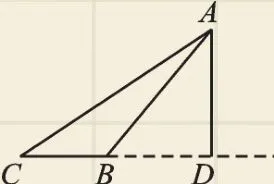
图8

我们在做任何题目时都不能掉以轻心，平时要多总结，多反思，查处每一次漏解的原因，养成认真审题、全面思题、严谨做题的好习惯！