圆的知识考查
2018-04-25成晓明
成晓明

圆的知识是初中数学知识中的一个重要组成部分,也是中考必考知识点.纵观各地中考试卷中对圆的知识的考查,主要体现在以下三个方面:一是重视圆的核心基础知识的考查,二是重视圆中数学思想方法的考查,三是重视圆与其他知识的整合考查.现结合具体考题进行分析点评,希望能对同学们系统复习有所帮助.
一、圆的核心基础知识
例1 (2017·南通)如图1,圆锥的底面半径为2,母线长为6,则侧面积为_____.
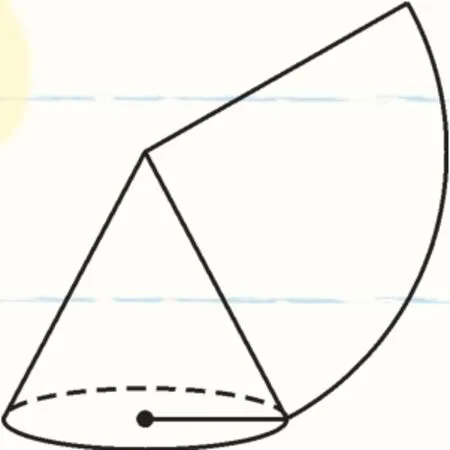
图1
【解答】根据圆锥的侧面积公式有:πrl=π×2×6=12π.
【点评】本题主要考查了圆锥侧面积公式S锥侧=πrl.
例2 (2017·南通)已知∠AOB,作图.步骤1:在OB上任取一点M,以点M为圆心,MO长为半径画半圆,分别交OA、OB于点P、Q;步骤2:过点M作PQ的垂线交于点⁀C;步骤3:画射线OC.则下列判断:①;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( ).
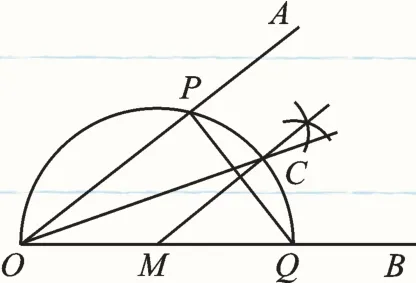
图2
A.1 B.2 C.3 D.4
【解答】∵OQ为直径,∴OA⊥PQ.
∵MC⊥PQ,
∴OC平分∠AOB,结论①④正确.
∵∠AOB的度数未知,∠POQ和∠PQO互余,
∴∠POQ不一定等于∠PQO,
∴OP不一定等于PQ,结论③错误.
综上所述:正确的结论有①②④.故选C.
【点评】本题考查了尺规作图、圆周角定理以及垂径定理等知识,熟练运用这些知识进行分析、判断是正确解题的关键.
例3 (2017·徐州)如图3,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为D,AB=BC=2,则∠AOB=______°.
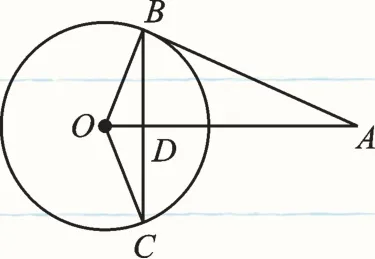
图3
【解答】∵OA⊥BC,BC=2,
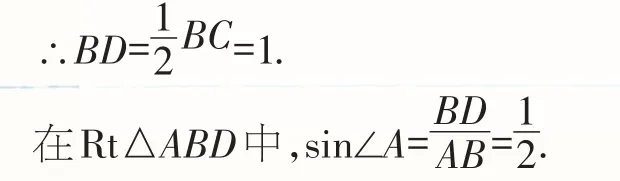
∴∠A=30°.
∵AB切⊙O于点B,
∴∠ABO=90°,
∴∠AOB=60°.
【点评】本题主要考查圆的切线性质、垂径定理和特殊角的三角函数值.
二、圆中数学思想方法
圆中蕴藏的数学思想方法众多,如分类讨论、数形结合、方程思想等,尤其是分类讨论的数学思想和方程思想的应用最为广泛.
例4 (2012·广元)平面上有⊙O及一点P,P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为_______cm.
【解答】当点P在圆内时,则直径=6+2=8,所以半径是4cm;
当点P在圆外时,直径=6-2=4,所以半径是2cm.
综上:⊙O的半径为4或2cm.
【点评】解决本题的关键是要对点和圆的位置关系分点在圆内和点在圆外两种情况考虑.
例5 (2013·兰州)如图4是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm,则该输水管的半径为________cm.
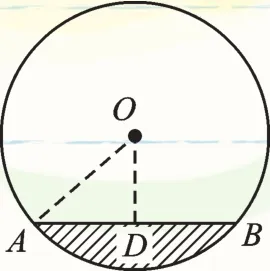
图4
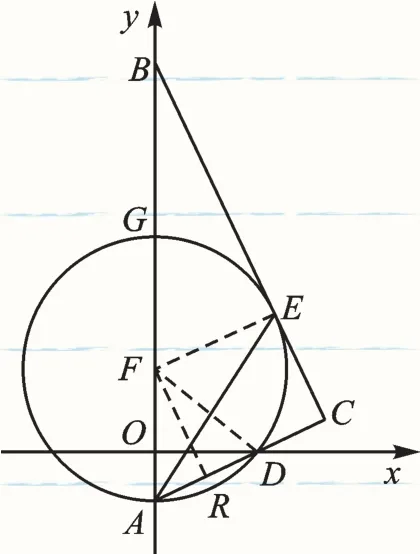
图5
【解答】如图4所示:过点O作OD⊥AB于点D,连接OA,
∵OD⊥AB,

设OA=r,则OD=r-2,
在Rt△AOD中,r2=(r-2)2+42,解得r=5.
【点评】本题考查的是垂径定理的应用及勾股定理,根据题意过圆心作弦的垂线是常用辅助线,利用方程是解决此题的关键.
例6 (2017·盐城)如图5,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.(1)求证:BC是⊙F的切线;(2)若点A、D的坐标分别为A(0,-1),D(2,0),求⊙F的半径;(3)试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.
【解答】(1)证明:连接EF,
∵AE平分∠BAC,
∴∠FAE=∠CAE,
∵FA=FE,
∴∠FAE=∠FEA,
∴∠FEA=∠EAC,
∴FE∥AC,
∴∠FEB=∠C=90°,
即BC是⊙F的切线.
(2)连接FD,设⊙F的半径为r,
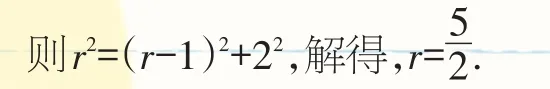
(3)AG=AD+2CD.证明:
王莉娜[15]认为,虽然碑学观念在“扬州八怪”那里还没有形成完整的体系,无论在笔法上,还是在理论上均没有臻于成熟与完善,但事实证明“扬州八怪”已经受到碑学的深刻影响。在“扬州八怪”书风中,特别是以“拙”、“古”、“厚”为突出特征并体现于诸位书家的艺术风格中的事实,表明了其特点均源于碑学,他们不计较技法的完美与精细,重要的是追求精神与神采,表现出“大巧若拙”之美。打破了清以来帖学衰弱的僵化模式,从而最终成就了“扬州八怪”这股丑拙的书风。
作FR⊥AD于R,则∠FRC=90°,
又∠FEC=∠C=90°,
∴四边形RCEF是矩形,
∴EF=RC=RD+CD,
∵FR⊥AD,
∴AR=RD,
【点评】本题考查切线的判定、垂径定理的应用、矩形的判定和性质等知识,掌握切线的判定定理和领悟方程思想是解题的关键.
三、圆与其他知识的整合
将圆的知识与三角形的全等、相似、四边形、解直角三角形、函数等知识的有机整合是中考命题的热点,这类题很好地考查同学们的综合解题能力.
例7 (2017·无锡)如图6,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于________.
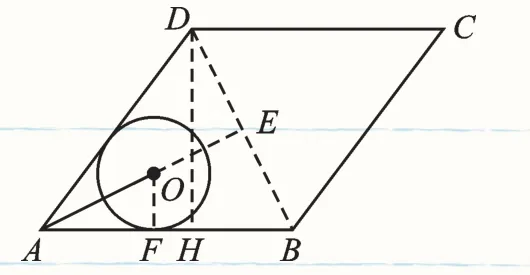
图6
【解答】如图6,作DH⊥AB于H,连接BD,延长AO交BD于E.
∵菱形ABCD的边AB=20,面积为320,
∴AB·DH=320,∴DH=16,
在Rt△ADH中,
∴HB=AB-AH=8,
在Rt△BDH中,
设⊙O与AB相切于F,连接OF.
∵AD=AB,OA平分∠DAB,
∴AE⊥BD,
∵∠OAF+∠ABE=90°,∠ABE+∠BDH=90°,
∴∠OAF=∠BDH,
∵∠AFO=∠DHB=90°,
∴△AOF∽△DBH,

【点评】本题综合考查了切线的性质、菱形的性质、勾股定理、相似三角形的判定和性质等知识,解题的关键是根据题意合理添加辅助线.
