问渠那得清如许，为有源头活水来——从教材习题到“圆”的中考考题

陈书奎

一、圆的定义

例1（苏科版《数学》九上第41页思考与探索）如图1，AB是⊙O的直径，C是BA延长线上一点，点D在⊙O上，且CD=OA，CD的延长线交⊙O于点E，若∠C=20°，求∠BOE的度数.

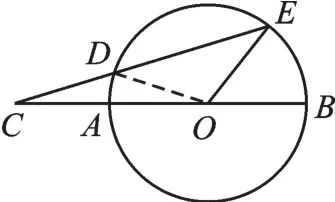
图1

图2

【解析】如图1，连接OD，由CD=OA可知CD=OD，那么∠COD=∠C=20°，得∠EDO=∠COD+∠C=40°，又因为OD=OE，得∠E=∠EDO=40°，最后可知∠BOE=∠C+∠E=60°.

【点评】此题考查了三角形的外角性质，解题的关键是抓住同圆的半径相等这一基本性质，连接半径构造等腰三角形解决问题.上述两条性质是题目中常见的隐含条件，同学们要善于挖掘应用.

【拓展】（2012·日照）如图2，过A、C、D三点的圆的圆心为E，过B、F、E三点的圆的圆心为D.如果∠A=63°，那么∠ABC=_______.

【解析】如图2，连接CE、DE，根据同圆的半径相等不难发现图中有三个等腰三角形：△AEC、△CED、△DEB，由∠A=63°算出∠AEC=54°，可知AEC=18°.

例2（苏科版《数学》九上第40页练习第3题）已知矩形ABCD的对角线AC、BD相交于点O.点A、B、C、D是否在以点O为圆心的同一个圆上？为什么？

【解析】由矩形的性质可得OA=OB=OC=OD，所以点A、B、C、D在以点O为圆心的同一个圆上.

【点评】解决这类问题同学们要抓住圆定义的本质，也就是圆是到定点距离等于定长的点的集合.此题是这一本质的静态呈现，而近几年的中考中更多的是从动态角度进行判断和应用.

【拓展1】（2014·成都）如图3，在边长为2的菱形ABCD中，∠A=60°，M是边AD的中点，N是AB上的一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，求A′C的最小值.

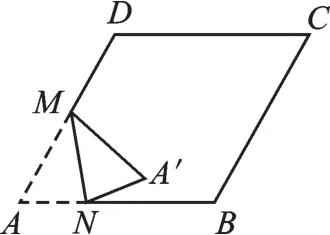
图3

图4

【解析】由MA=MA′，故点N在从A到B的移动过程中，A′的运动轨迹是以M为圆心，MA′为半径的圆弧，将问题转化为圆外一点到圆上点的最短距离.如图4，当A′在MC上时，A′C的长度最小.过点C作CE⊥AD交AD的延长线于点E，由CD=2，MD=1，∠EDC=60°，可得∠ECD=30°，DE=1，EC=3，EM=2，MC=7，所以A′C=7-1.

【拓展2】（2016·淮安）如图5，在Rt△ABC中，∠C=90°，AC=6，BC=8，点F在边AC上，并且CF=2，E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是_______.

图5

图6

【解析】由PF=CF，故点P的运动轨迹是以F为圆心，FC为半径的圆弧.此问题就转化为求与圆相离的直线上一点与圆上一点距离的最小值，不难想到过点F作FH⊥AB于点H，如图6，当点P在FH上时，这个距离最小.下面我们可以利用∠A的正弦和AF长度求出FH=3.2，于是PH=FH-PF=1.2，即点P到边AB的最小距离是1.2.

二、圆的对称性

例3（苏科版《数学》九上第48页练习第3题）如图7，⊙O的直径为10，弦AB的长为8，点P在AB上运动，求OP的取值范围.

【解析】过点O作OH⊥AB于H，连接OB，OP的最小值等于OH长，OP的最大值是半径OB，长为5，根据垂径定理可得=4，再依据勾股定理算出OH=3，故3≤OP≤5.

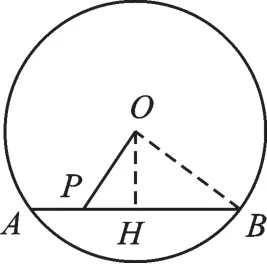
图7

【拓展1】如图8，一座弧形桥的跨度AB长为40米，桥离水面最大距离CD为10米，一条水面以上宽度为30米，高度为6米的船能否顺利通过这座桥？

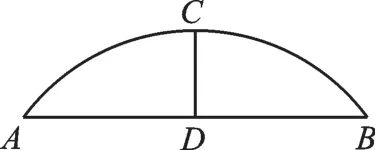
图8

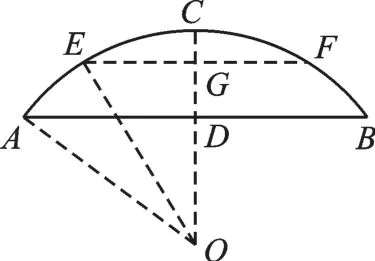
图9

【解析】如图9，设弧形桥所在圆的圆心为O，半径为r，EF=30，在Rt△AOD中，r2=202+（r-10）2，解得r=25，所以OD=15，在Rt△OEG中，20，GD=OG-OD=5（米）＜6（米），故船不能顺利通过这座桥.

【拓展2】（2013·内江）如图10，在平面直角坐标系中，以原点O为圆心的圆过点（13，0），直线y=kx-3k+4与⊙O交于B、C两点，则弦BC的长的最小值_______.

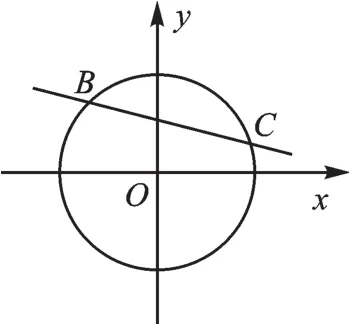
图10

图11

【解析】由直线的解析式可以看出当x=3时，y=4，说明直线经过定点（3，4），设这个定点为点H，如图11，当BC⊥OH时，BC最短，连接OC，易知=12，故弦BC长的最小值为24.

三、灵活转化圆中角

例4（苏科版《数学》九上第56页练习第3题）如图12，点A、B、C、D在⊙O上，∠ACB=∠BDC=60°，BC=3，求△ABC的周长.

图12

【解析】根据同弧所对的圆周角相等可知∠A=∠D=60°，易得△ABC为等边三角形，周长为9.

【点评】同弧所对的圆周角相等是圆中重要的条件，利用这一性质可以为全等和相似做铺垫.

【拓展1】（2015·德州）如图13，⊙O的半径为1，A、P、B、C是⊙O上的四个点，∠APC=∠CPB=60°.

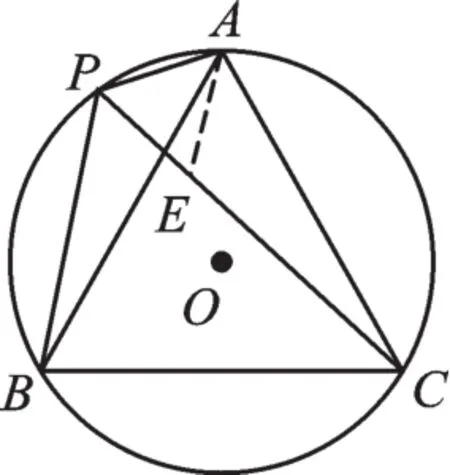
图13

（1）判断△ABC的形状：_________；

（2）试探究线段PA、PB、PC之间的数量关系，并证明你的结论.

【解析】由上一例题可判断△ABC为等边三角形.第（2）小题结论是PA+PB=PC，证明线段和差等量关系一般可用“截长补短”法.如：在PC上取点E，使PE=PA，易得△APE为等边三角形，所以∠PAE=∠BAC=60°，则∠PAB=∠EAC，再由AB=AC，∠PBA=∠ECA，可得△APB≌△AEC，所以PB=EC，故PA+PB=PC.

【拓展2】（2015·宿迁）已知：⊙O上两个定点A，B和两个动点C，D，AC与BD交于点E.

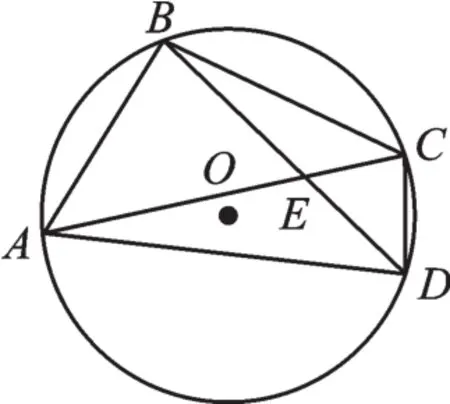
图14

图15

（1）如图14，求证：EA·EC=EB·ED；

（3）如图16，若AC⊥BD，点O到AD的距离为2，求BC的长.

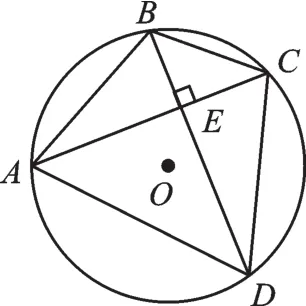
图16

图17

【解析】（1）根据同弧所对的圆周角相等得到∠EAD=∠EBC，∠BCE=∠ADE，故△AED∽△BEC，得AE∶BE=DE∶CE，所以EA·EC=EB·ED.

（3）如图17，作直径DF，连接AF，作OH⊥AD于H，易得∠ACD=∠HOD，∠CED=∠OHD，得出∠ADF=∠BDC，进一步可知，从而BC=AF=2OH=4.

同学们，在中考中很多考题就是课本例题、习题的变式或延伸，只要我们善于挖掘教材里题目的价值，做到举一反三，相信你在中考考场上能如鱼得水！