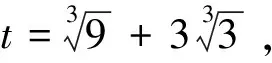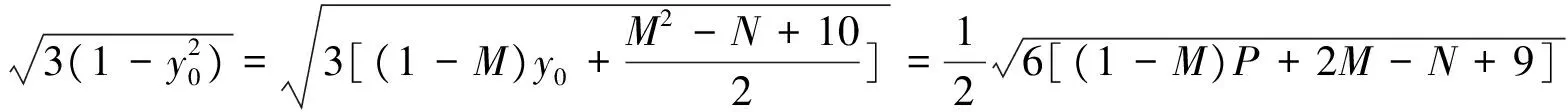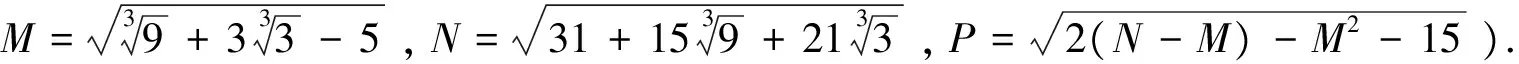《数学通讯》问题219的准确最值

首都师范大学附属回龙观育新学校

牛文政 (邮编：102208)

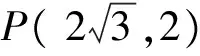
文[2]指出：该问题距离的最小值存在,虽不能求出其准确值,但可求出其近似值，其近似值为2.46501，此时椭圆上的点的坐标近似于(1.563435 , 0.430376).

事实上，这个近似值是正确的，但一定不能求出其准确值么？其实这个准确值是可以得到的，虽然它表达起来有点困难，本文将给出其准确值的表达.

为了使本文完整，下面引用文[2]的部分解题过程(该过程是正确的)：

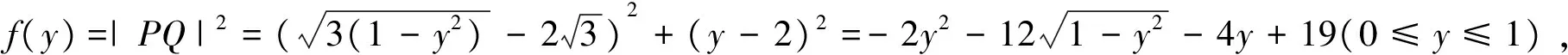
下面我们求f′(y)=0在(0,1)上存在唯一零点y=y0.

当0

①

文[2]之后证明了方程①在(0,1)内有唯一的实根y=y0.虽然上述过程是正确的，但下面论述却有欠妥之处：“如上面这样的一元四次实系数方程①,我们仅能判断其是否有实根,却不能求出所存在的实根的准确值(理论值).由于这种方程的实根的准确值(理论值)不能求出.因而PQ的最小值PQ0的准确值(理论值)也就不能求出.对于本争鸣问题,我们虽不能求出PQ0的准确(理论)值,但可以通过近似计算求出它的精确到一定数位的近似值(列).”

我们知道，实系数一元四次方程是可以求解的，我们运用费拉里与卡尔丹的古典方法，便可以将方程①在的(0,1)内的实根解出，过程如下：

方程①可化为：

y4+2y3=-9y2+2y+1，配方得：

(y2+y)2=-8y2+2y+1，取待定的z∈R，再配方：

②

令z=t+3，得：(t+3)3-9(t+3)2-36=0，即t3-27t-90=0，

令t=u+v,得：(u+v)(3uv-27)+u3+v3-90=0，

③

④

方程④无实数根，方程③在(0,1)上的实数根为：

由方程③知：

则

1 王淼生.“争鸣”栏目问题219[J].数学通讯,2012(9):30

2 汤先健，汤敬鹏. “争鸣”栏目问题219[J].评论，2013(1)