改进粒子群优化-Elman算法在发动机曲轴脉宽预测中的应用
2018-04-24孟蓉歌张春化梁继超
孟蓉歌 张春化 梁继超
1.长安大学汽车学院,西安,7100642.陕西重型汽车有限公司,西安,710200
0 引言
曲轴信号是燃油喷射正时控制的基准,仅靠曲轴的机械结构无法精确判断曲轴相位,燃油喷射控制精度不高。如60-2结构的曲轴齿盘,其曲轴转角所能识别的精度仅为6°,以6°曲轴转角为依据进行喷油控制精度明显不够,而目前可用于高精度喷油控制的电子编码器多为进口,价格昂贵。由此,有必要对曲轴信号脉宽进行准确预测,根据预测结果倍频曲轴信号,从而提高发动机燃油喷射的控制精度。利用锁相环与分频器实现锁相倍频,硬件电路复杂,元器件的参数设计调整相对困难,同时信号的倍频数也无法灵活设置。杨骐菲等[1]利用单片机实现了信号倍频,马志磊等[2]利用TC1728对曲轴信号进行了判缸模式研究。这两种方法中所用倍频方式受单片机计数器位数的影响,脉宽预测精度受到限制。文献[3-4]基于最小二乘算法实现了曲轴信号脉宽预测,这种方式预测精度较低且瞬态工况下脉宽预测的跟随性较差。
对此,本文提出采用改进粒子群优化(PSO)-Elman神经网络的方法(以下简称“PSO-Elman算法”)对曲轴脉宽信号进行预测。陈杰等[5]将PSO算法优化Elman神经网络用于短期电力负荷预测;张俊玲等[6]选用惯性权重线性递减的PSO算法优化了Elman神经网络并将其用于无模型控制中;颜宏文等[7]用关联规则对PSO-Elman算法预测结果进行修正,提高了算法的预测精度。这几种采用PSO算法优化Elman的方法没有对算法陷入局部最优的情况进行处理,算法易出现早熟现象。本文针对基本PSO算法种群过早陷于当前局部最优,未能对整个解空间进行充分搜索的问题,通过改变惯性权重的修正方法使得PSO算法得到改进,改善了算法搜索的全局性,使算法能以较快速度跳出局部最优,提高网络收敛速度。
1 改进PSO算法优化Elman神经网络
1.1 Elman神经网络
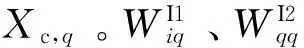
x(k)=ψXc(k-1)
Xc(k)=f(WI1u(k-1)+WI2x(k))
y(k)=g(WLXc(k))
式中,f(·)、g(·)分别为隐含层与输出层的激励函数;ψ为反馈层的自连接增益因子。
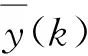
1.2 改进PSO算法
粒子群算法最初用于模拟鸟群觅食过程[8]。粒子群中的每个粒子代表问题的一个潜在解,粒子通过自身的个体认知与群体中其他成员的社会认知动态地更新自己的速度与位置以优化群体行为。粒子速度和位置更新公式为
vid(t+1)=w(t)vid(t)+c1r1(pid-xid(t))+
c2r2(pgd-xid(t))
(1)
xid(t+1)=xid(t)+γvid(t+1)
(2)
式中,vid、xid分别为粒子i的速度和位置;c1为粒子跟踪个体历史最优的权重系数;c2为粒子跟踪社会认知的权重系数;pid、pgd为粒子个体和群体的历史最优位置;r1、r2为[0,1]内的随机数;w为惯性权重。
惯性权重w和加速因子c1、c2是影响算法优化性能的重要参数,王东风等[9]研究了不同参数组合对算法优化性能的影响,推荐了一组固定参数组合和一种变化的参数设置方法。惯性权重w用于平衡粒子的全局搜索能力和局部搜索能力,w较大时算法具有全局收敛性,但运算量较大,w较小时算法易收敛,但也易陷入局部最优点。w一般按线性递减算法取值[10]。带压缩因子的惯性权重能够克服线性递减算法的不足[11],但对算法陷入局部最优没有给出具体的解决方法。对此,本文提出根据算法迭代结果动态设置惯性权重以改进基本粒子群优化的方法。将本次适应度函数的值与上次进行比较,若两次适应度值变化在0.01%内则认为算法本次陷入局部最优,陷入局部最优的代数加1,否则算法未陷入局部最优,代数清零。算法求解过程中如果连续5代寻找到的最优值变化在0.01%内则认为算法陷入局部最优。算法未陷入局部最优时惯性权重按线性递减更新;算法陷入局部最优时则根据陷入局部最优的代数按比例增大惯性权重,以使算法尽快跳出局部最优点。改进PSO算法与PSO算法的主要区别在于对惯性权重的修正方法不同,如表1所示。

表1 PSO算法与改进PSO算法惯性权重修正方法
1.3 改进PSO-Elman神经网络
改进PSO-Elman神经网络步骤如下:
(1)采集输入输出样本数据,并进行归一化处理,创建Elman神经网络。
(2)根据Elman神经网络结构确定粒子群规模,初始化粒子速度、位置、惯性权重、加速因子及迭代次数。
(3)计算群体中各粒子的适应度值及全局最优适应度值。采用误差平方和函数为学习指标函数,即粒子的适应度函数。适应度值定义为
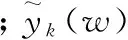
如果该粒子的当前适应度值优于其历史最优位置的适应度值,则更新该粒子个体最优位置。如果所有粒子中个体最优位置所对应的适应度值优于当前全局最优适应度值,则更新全局最优位置。
(4)采用式(1)、式(2)对各粒子的速度和位置进行更新,产生下一代粒子群。
(5)判断算法是否陷入局部最优。适应度函数优化过程中,若连续5代寻找到的最优值变化在0.01%内,则认为算法陷入局部最优(陷入局部最优的代数设为gJ),按w=w+gJ/0.1更新惯性权重,w最大取1.2,超出时则取1.2。若未陷入局部最优则惯性权重按w=0.9-0.5g/M(g为迭代次数,M为种群规模)进行更新,w最小取0.68。
(6)判断迭代次数是否到达,到达则停止迭代;否则进入步骤(3)重复。
(7)利用改进PSO算法优化所得参数(输入层至隐层权值WI1、反馈层至隐层权值WI2、隐层至输出层权值WL、隐层阈值与反馈层阈值)训练Elman神经网络。
(8)训练结果反归一化,输出。
2 改进PSO-Elman算法的应用
2.1 实验装置
实验用发动机为一台6缸增压中冷YC6G270-30型柴油机。发动机主要参数如表2所示。

表2 发动机主要参数
2.2 网络结构及种群初始化
稳态工况下分别对650 r/min、1 000 r/min、1 200 r/min与2 000 r/min时的曲轴脉宽进行预测,瞬态工况下对1 030 r/min波动时的曲轴信号脉宽进行预测。为便于确定粒子规模,每6个脉宽作为一组样本数据,前5个为输入脉宽,第6个为预测脉宽。各工况下取训练样本500组,测试样本100组。将样本数据归一化后输入所创建的Elman神经网络中。
网络隐层传递函数取tansig和logsig,反向传播函数取traingdx和trainlm,输出层传递函数取tansig与purelin分别组合进行预测。结果发现隐层传递函数取tansig或logsig对训练结果影响不大;反向传播函数取trainlm时比traingdx训练结果精度稍有提高,但网络训练时间明显增长;输出层传递函数取线性传递函数purelin时,网络训练精度明显更高(相较采用tansig函数)。最终选择tansig为所设计网络的隐层传递函数,traingdx为反向传递函数,purelin为输出层传递函数。
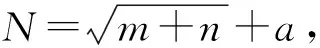
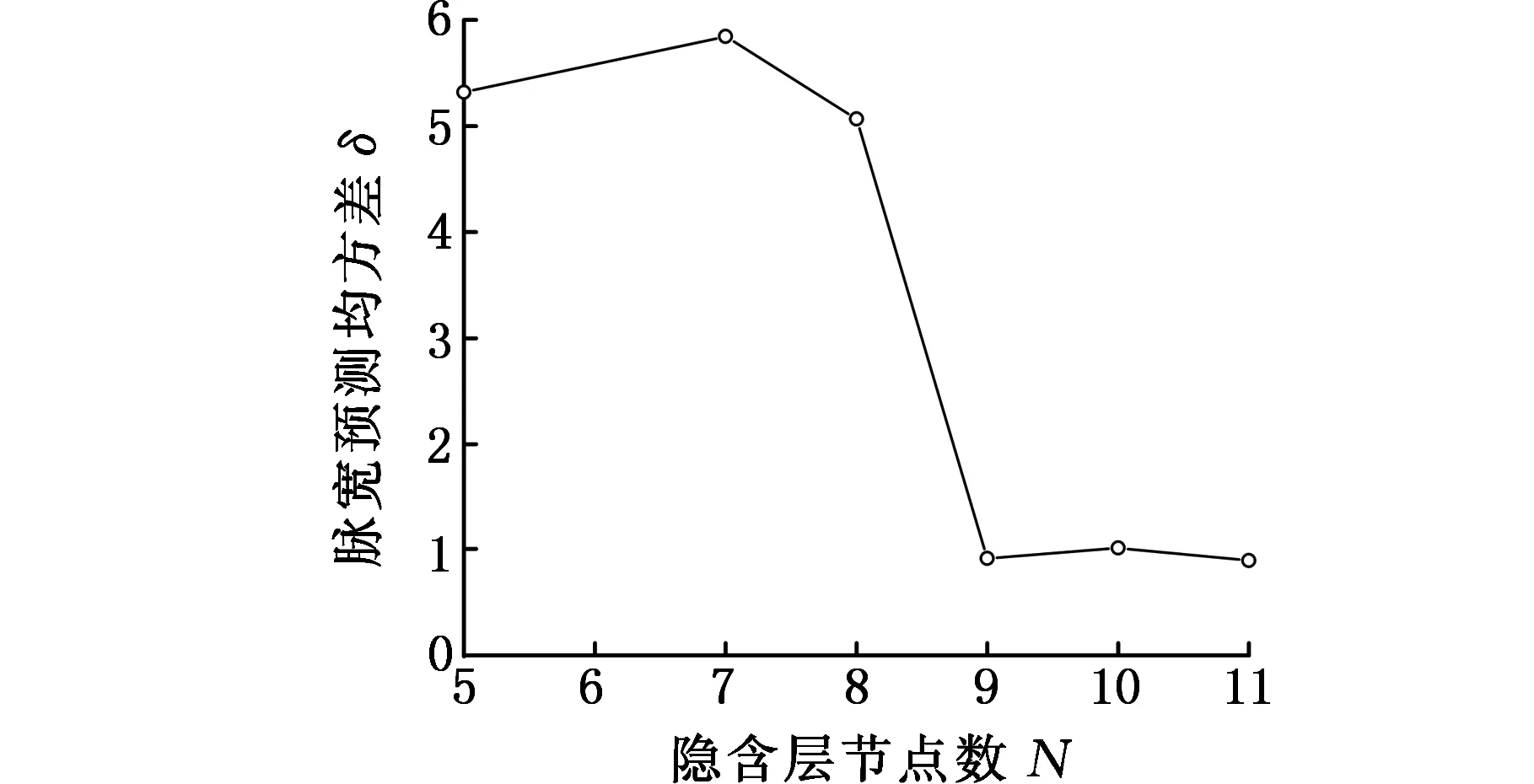
图2 预测结果均方差与隐层节点数关系Fig.2 The relationship between mean square error andthe number of hidden layer nodes
根据实际工程需要,网络最大训练步数设为1 000,误差容限取0.001。利用改进PSO算法对Elman神经网络进行优化,各粒子由WI1、WI2、WL、输入层阈值b1及输出层网络阈值b2组成,粒子编码格式如图3所示。
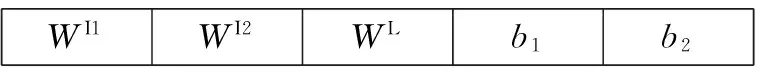
WI1WI2WLb1b2
图3粒子编码格式
Fig.3Codingformatofparticle
因此,网络权值的个数为5×9+9+9×1=63个,阈值为9+1=10个,PSO算法粒子的长度为73。设定粒子个数为40,最大迭代次数为100,加速因子取c1=2.05、c2=0.5[13]。
2.3 结果及分析
2.3.1不同工况下脉宽预测结果比较
曲轴脉宽信号采样周期为2.5 μs,稳态工况下以怠速650r/min为例,其脉宽预测结果如图4所示。其他稳态转速工况下可得相似的预测波形。
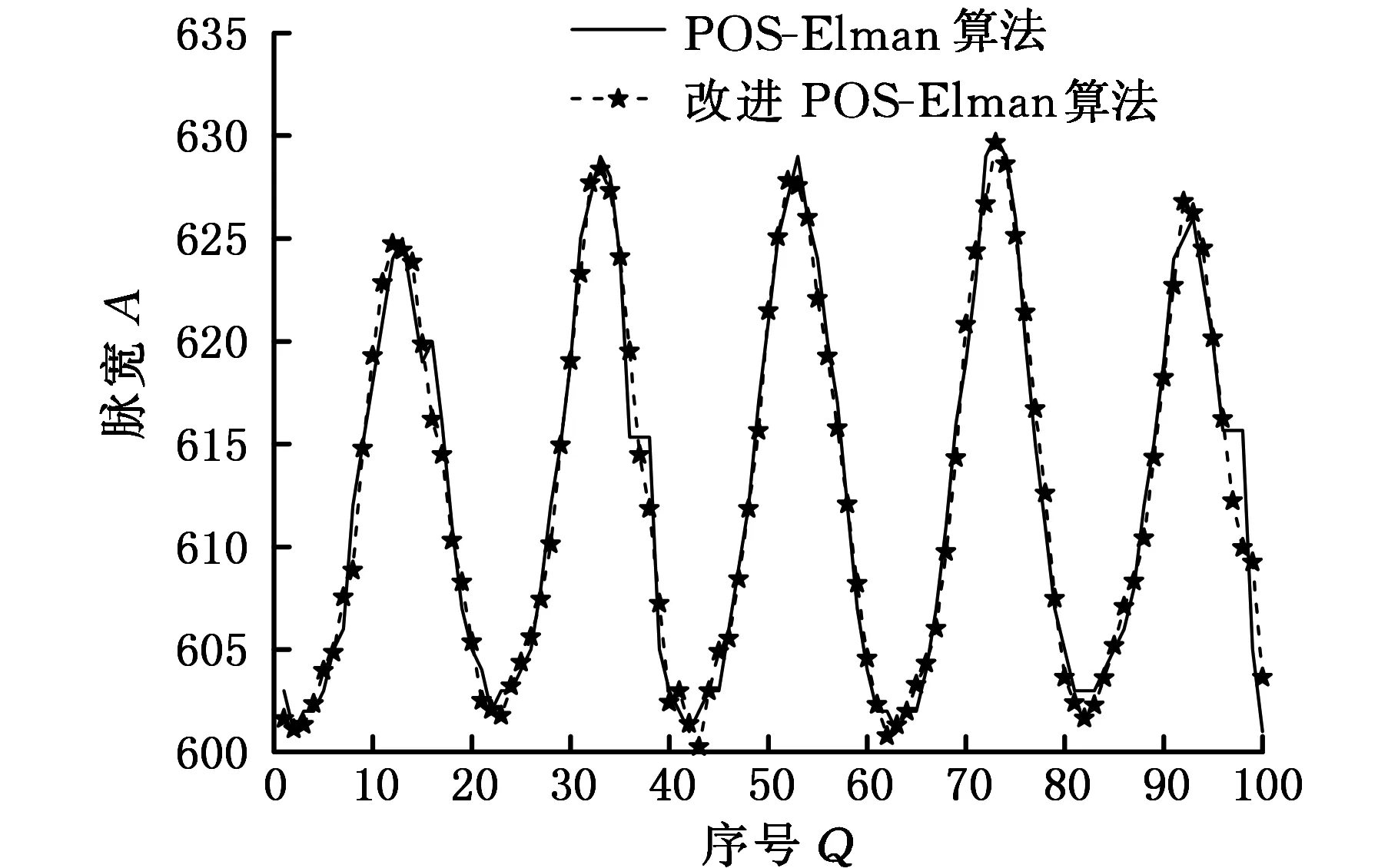
图4 650 r/min稳态工况脉宽预测结果Fig.4 Prediction result of engine speed under steady-state operating condition 650 r/min
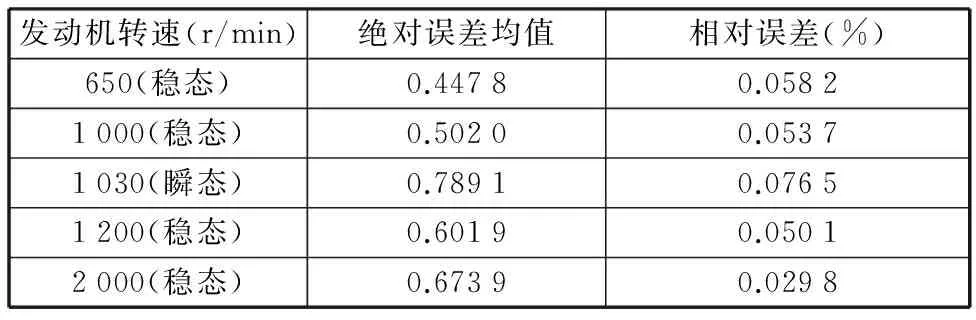
瞬态工况下将1 030 r/min波动时的转速预测值与实际值进行比较,结果如图5所示。各工况下曲轴脉宽预测误差结果见表3。
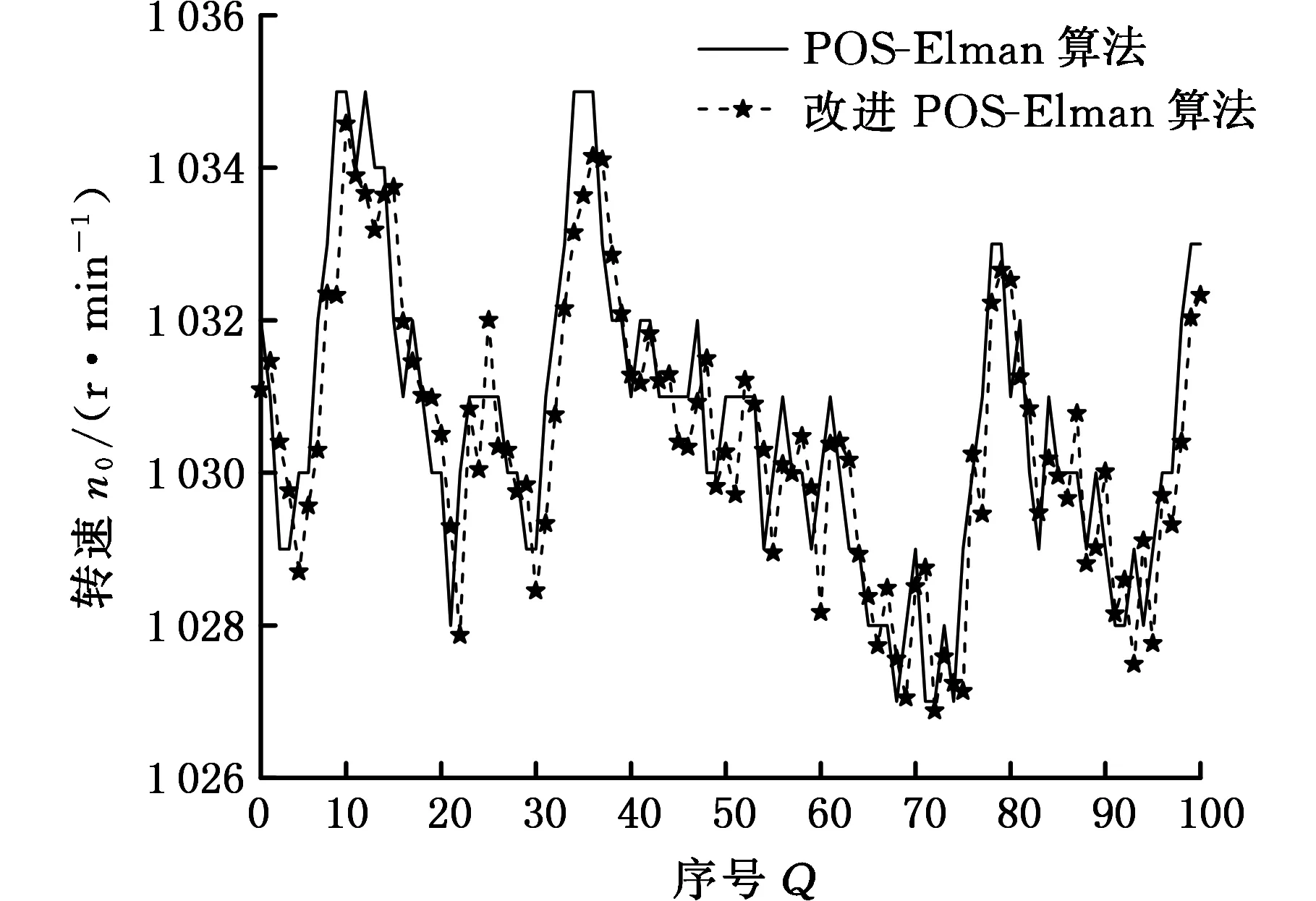
图5 1 030 r/min瞬态工况转速预测结果Fig 5 Prediction result of engine speed under transient operating condition 1 030 r/min
发动机转速(r/min)绝对误差均值相对误差(%)650(稳态)0.44780.05821000(稳态)0.50200.05371030(瞬态)0.78910.07651200(稳态)0.60190.05012000(稳态)0.67390.0298
由表3可见,随着发动机转速的增大,脉宽预测绝对误差均值略有增大,怠速工况下绝对误差均值最小,相对误差随着发动机转速的增加明显减小。瞬态工况转速在1 030 r/min波动时脉宽预测绝对误差与相对误差均为最大。
2.3.2不同算法预测结果对比
为验证算法在小样本情况下的预测能力,任取10个怠速工况下的连续采样脉宽数据,分别采用最小二乘算法、训练好的Elman神经网络、PSO-Elman神经网络及改进PSO-Elman神经网络进行预测,预测结果如图6所示。脉宽预测绝对误差均值见表4。
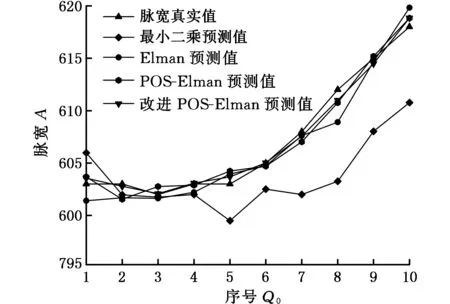
图6 不同模型脉宽预测结果Fig.6 Prediction results of different models
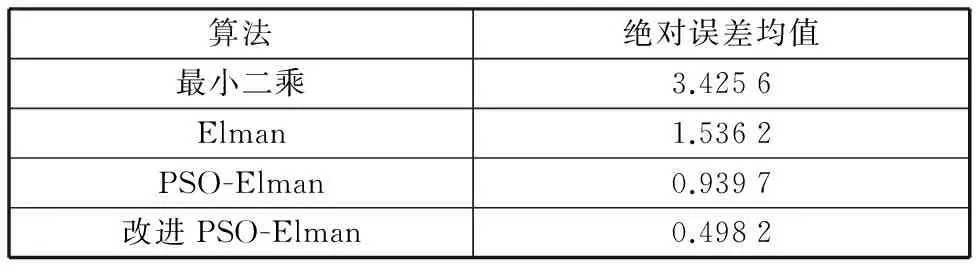
算法绝对误差均值最小二乘3.4256Elman1.5362PSO-Elman0.9397改进PSO-Elman0.4982
图7所示为脉宽预测相对误差。
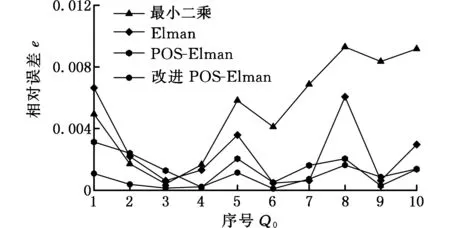
图7 相对误差结果比较Fig.7 Comparison of relative error
图8为改进PSO-Elman神经网络算法与PSO-Elman神经网络算法适应度函数变化曲线。
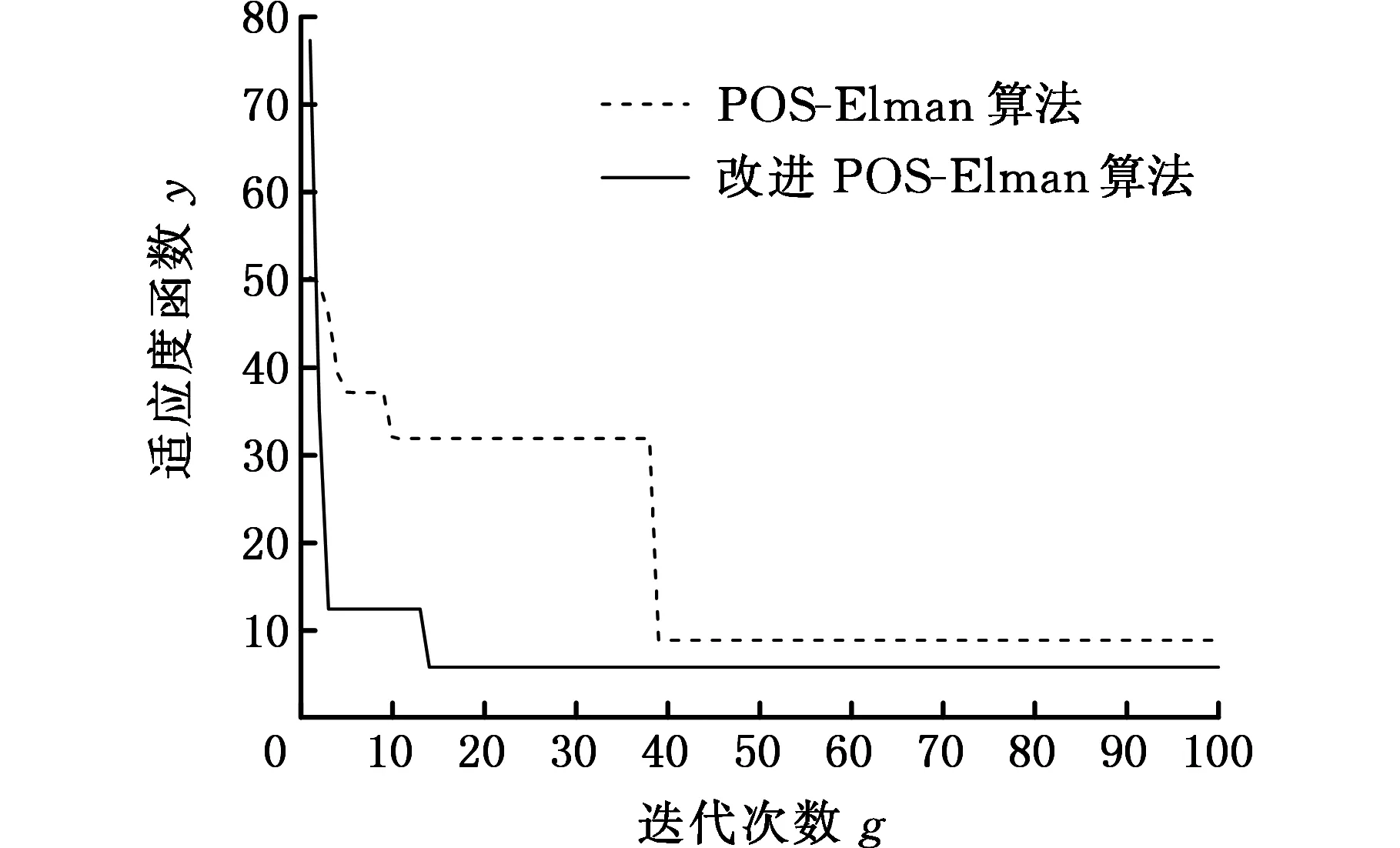
图8 适应度曲线对比图Fig.8 Comparison graph of adaptability curves betweenPSO-Elman and advanced PSO-Elman
由图8可见,改进PSO-Elman算法能够以较快的速度跳出局部最优,经13次迭代算法可达稳定值,同时其收敛精度明显高于PSO-Elman神经网络算法。由于PSO算法采用并行计算,同时受种群规模及维数影响,故文中所用神经网络均采用离线训练方式。
3 结论
(1)改进PSO-Elman神经网络算法能够准确预测发动机曲轴脉宽信号,可用于信号倍频以提高发动机喷油控制的精度。瞬态工况时因为发动机加速度变化大,脉宽预测精度略低于稳态。
(2)改进PSO-Elman神经网络算法根据迭代陷入局部最优的代数修改惯性权重使算法能够以较短步长跳出局部最优,有效地提高了算法的收敛速度。改进PSO-Elman神经网络算法预测精度明显高于最小二乘、Elman神经网络与PSO-Elman神经网络算法的预测精度。
参考文献:
[1] 杨骐菲,申立中,王贵勇,等. 高压共轨柴油机曲轴信号倍频研究[J]. 科学技术与工程,2011,25(11):6065-6070.
YANG Qifei, SHEN Lizhong, WANG Guiyong, et al. Study of High Pressure Common Rail Diesel Crank Sensor Signal Frequency Multiplier[J]. Science Technology and Engineering,2011,25(11):6065-6070.
[2] 马志磊,王贵勇,申立中. 基于TC1728的高压共轨柴油机判缸研究[J]. 车用发动机,2015,2(1):6-16.
MA Zhilei, WANG Guiyong, SHEN Lizhong. Cylinder Detection for High-pressure Common Rail Diesel Engine Based on TC 1728[J]. Vehicle Engine,2015,2(1):6-16.
[3] WANG Junmin, SARLSHKAR J V. Engine Crankshaft Position Tracking Algorithms Applicable for Given Arbitrary Cam and Crank-shaft Position Signal Patterns[J]. SAE Technical Paper Series,2007-01-1597.
[4] LETEINTURIER P, BENNING J. Enhanced Engine Position Acquisition & Treatment[J]. SAE Technical Paper Series, 1999-01-0203.
[5] 陈杰,高翠云,胡翀. 基于PSO-Elman神经网络的短期电力负荷预测[J]. 安徽建筑大学学报,2016,24(1):82-86.
CHEN Jie, GAO Cuiyun, HU Chong. Short-term Electric Load Forecasting Based on PSO-Elman Neural Network[J]. Journal of Anhui Institute of Architecture & Industry,2016,24(1):82-86.
[6] 张俊玲,陈增强,张青. 基于粒子群优化的Elman神经网络无模型控制[J]. 智能系统学报,2016,11(1):49-54.
ZHANG Junling, CHEN Zengqiang, ZHANG Qing. Elman Model-free Control Method Based on Particle Swarm Optimization Algorithm [J]. CAAI Transactions on Intelligent Systems,2016,11(1):49-54.
[7] 颜宏文,邹丹. 基于关联规则的PSO-Elman短期风速预测[J]. 计算机工程与应用,2017(1):1-10.
YAN Hongwen, ZOU Dan. Short-term Wind Speed Forecasting Based on PSO-Elman Optimized by Association Rule[J]. Computer Engineering and Applications,2017(1):1-10.
[8] 干旭波,姚栋伟,吴锋,等. 基于PSO算法的SCR尿素热解动力学参数优化[J]. 内燃机工程,2016,37(3):83-93.
GAN Xubo, YAO Dongwei, WU Feng, et al. Kinetic Optimization of Urea-SCR Thermal Decomposition Based on PSO Algorithm[J]. Chinese Internal Combustion Engine Engineering,2016,37(3):83-93.
[9] 王东风,孟丽. 粒子群优化算法的性能分析和参数选择[J]. 自动化学报,2016,42(10):1552-1561.
WANG Dongfeng, MENG Li. Performance Analysis and Parameter Selection of PSO Algorithms[J]. Acta Automatica Sinica,2016,42(10):1552-1561.
[10] 张任,胥芳,陈教科,等. 基于PSO-RBF神经网络的锂离子电池健康状态预测[J]. 中国机械工程,2016,27(21):2975-2981.
ZHANG Ren, XU Fang, CHEN Jiaoke, et al. Li-ion Battery SOH Prediction Based on PSO-RBF Neural Network[J]. China Mechanical Engineering,2016,27(21):2975-2981.
[11] 黄平. 粒子群算法改进及其在电子系统的应用[D].广州:华南理工大学,2012.
HUANG Ping. Improved Particle Swarm Algorithm and Its Application in Power System[D]. Guangzhou: South China University of Technology,2012.
[12] 浦健,程静. 基于PSO-Elman神经网络的汽轮机排汽焓在线预测计算[J]. 南京师范大学学报(工程技术版),2009,9(2):35-40.
PU Jian, CHENG Jing. Online Prediction and Calculation of Steam Turbine Exhaust Enthalpy Based on PSO-Elman Neural Network[J]. Journal of Nanjing Normal University(Natural Science Edition),2009,9(2):35-40.
[13] 陈波,潘海鹏,邓志辉. 基于PSO优化RBF神经网络的反应釜故障诊断[J]. 中国机械工程,2012,23(18):2204-2207.
CHEN Bo, PAN Haipeng, DENG Zhihui. Application of PSO-based RBF Neural Network in Fault Diagnosis of CSTR[J]. China Mechanical Engineering,2012,23(18):2204-2207.
