求实际应用问题中最值的六种意识
2018-04-23周法青宋振苏
周法青 宋振苏
(1.江苏省大港中等专业学校 222043; 2.江苏省连云港开发区高级中学 222067)
周法青(1967.8-),男,江苏连云港人,学历,中学一级教师,优秀青年教师.
一、利用函数的单调性
函数的单调性是函数重要而基本的性质之一,也是解答最值问题的有效工具之一,因此在解答某些实际应用问题时,如能合理运用会使问题的求解简捷明快、事半功倍.

图1
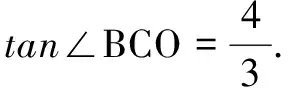
(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
思路(1)建立平面直角坐标系,设点B的坐标,借助题设求出B的坐标,进而求出BC的长;(2)先设OM的长为d,建立半径r关于d的函数,再借助题设条件求出d的范围,最后依据函数的单调性求出r的最大值.


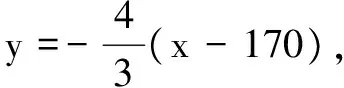
点评本题(2)借助直线BC与圆M相切建立了半径r关于d的函数(一次函数),再利用题设条件求出变量d的取值范围,最后运用一次函数的单调性求出半径r的最大值,进而使本题获解.
二、利用二次函数
二次函数是中学数学中重要的基本初等函数之一,也是解决实际应用问题的有效工具之一,解决某些实际应用的最值问题时,如果建构的函数模型是二次函数,可运用二次函数的有关知识进行求解.
例2 (2011年连云港模考题)某汽车租赁公司总共拥有汽车100辆,当每辆汽车的月租金为3000元时,可全部租出.若每辆汽车的月租金增加50元,未租出的汽车将会增加1辆,另外租出的汽车每辆每月需要维护费150元,未租出的汽车每辆每月还需要养护费50元.
(1)当每辆汽车的月租金定为3600元时,能租出多少辆车?
(2)当每辆汽车的月租金定为多少元时,租赁公司的月收益(一个月所获得的利润)最大?求出该最大月收益.
思路先根据题设搞清楚租出的和未租出的汽车数,建立函数关系,再运用数学知识求解.
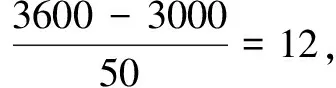

点评本题是一道汽车租赁中的实际应用问题,解答时借助二次函数的知识和图象,使问题轻松获解.当建构的函数模型是二次函数时,应运用二次函数的有关知识求解.
三、利用基本不等式
基本不等式是中学数学中重要的知识点和解题的模型与工具,也历届数学高考命题的必考考点.解答某些实际应用问题时,若建立的函数符合基本不等式的情境时,可适时灵活地运用基本不等式进行求解.

图2
例3 (2010年江苏卷)如图2,某兴趣小组测量电视塔AE的高度H(单位:m),如示意图,垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β.
(1)该小组已经测得一组α,β的值,且tanα=1.24,tanβ=1.20,请根据此数据算出H的值;
(2)该小组分析若干测得的数据后,发现适当调整标杆到电视塔的距离d(单位m),使α与β之差较大,可以提高测量精确度,若电视塔实际高度为125 m,问d为多少时,α-β最大?
思路(1)依据题设建立方程组求解;
(2)先建立tan(α-β)关于变量d的函数,再求tan(α-β)的最大值从而可使本题获解.



四、利用三角函数
三角函数也是中学数学中重要的基本初等函数之一,也是解决实际应用问题的有效工具之一,解决某些实际应用的最值问题时,如果建构的函数是三角函数模型,可运用三角函数的有关知识进行分析求解.
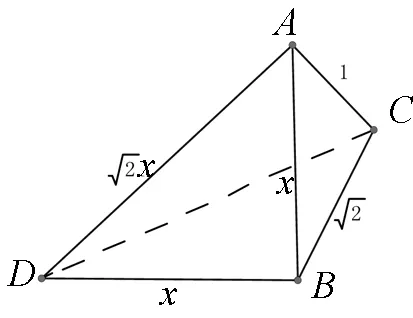
图3

思路先设DB=AB=x,分别在△ABC,△DBC中运用余弦定理,建立CD关于x的函数关系式,进而运用所学知识进行求解.

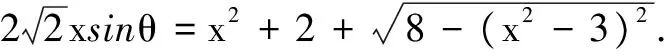
点评本题易运用余弦定理和勾股定理建立了函数关系,求解时借助换元法将问题进行转化为三角函数的最值问题,从而使貌似挺难的问题巧妙获解,体现了换元转化思想与三角函数的最值在解决实际问题中的妙用.
五、利用导函数
导数是研究函数的单调性和极值最值的重要工具,是中学数学中研究函数的图象和性质的重要手段之一,也是解决实际应用问题的有效工具之一,解决某些实际应用的最值问题时,如果能巧妙利用导数研究出函数的单调性,进而可求出其极值和最值.

图4
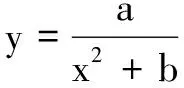
(1)求a,b的值;
(2)设公路L与曲线C相切于点P,而点P的横坐标为t,
①请写出公路L长度的函数解析式f(t),并写出其定义域;
②当t为何值时,公路L的长度最短?并且求出最短长度.
思路(1)可依据题设条件建立a,b方程组求解;
(2)先求出切线的斜率,再求切线方程,求出切线与坐标轴的交点坐标,求出公路L的长度(用t来表示),建立函数f(t),再运用所学知识求出其最小值.
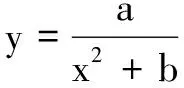


参考文献:
[1]中华人民共和国教育部.普通高中数学标准[M].北京:人民教育出版社,2017.
