表面温度计示值测量结果的不确定度分析与评定

张欢　郭浩　苏英

【摘要】 表面温度计是用于测量固体表面温度的仪器，被广泛应用于科研和生产中。本文通过建立数学模型以及对可能影响表面温度计示值测量结果的各种不确定来源的分析，对其测量结果的不确定度进行了评定。

【关键词】 表面温度计;测量结果;不确定度

【DOI编码】 10.3969/j.issn.1674-4977.2018.04.008

Uncertainty of Measurement Analysis and Evaluation of

the Surface Thermometer

ZHANG Huan， GUO Hao， SU Ying

（1. Liaoning Provincial Institute of Measurement， Shenyang 110004， China;

2. PetroChina JinXi PetroChemical Company， Huludao 125001， China）

Abstract： The surface thermometer is an instrument for measuring the surface temperature of an object. It is widely used in scientific research and production. By establishing the relative mathematical model and analyzing the sources of uncertainty which may affect the measurement results of the surface thermometer， the paper introduces the evaluation process of uncertainty.

Key words： surface thermometer;measurement result;uncertainty

表面温度计是用于测量固体表面温度的仪器，被广泛应用于航天、航空、能源、化工、纺织等科研和生产中。表面温度计由表面温度传感器和显示仪表组成。温度传感器是表面温度计的关键器件，直接决定了表面温度计的性能优劣。其测温原理是将表面温度计的温度传感器的感温元件紧密压在被测物体表面，由指示仪表来显示被测物体的表面温度（如图1）。

表面温度计校准装置主要在室温0～400℃温度范围内对表面温度计进行校准。测量方法依据JJF 1409-2013《表面温度计校准规范》，测量时采用的计量标准及其配套设备见表1。

目前知名厂家生产的经筛选后的表面温度计具有较好的重复性，可视为现有的最佳仪器。表面温度计温度范围为0～400℃，分度值分为0.1℃和1℃两种。

在校准表面温度计前，需检查表面温度源的表面热板是否存在污垢、油污，以及表面是否平整，保证表面温度计感温元件与表面温度源的表面热板得到良好接触。对表面温度计进行校准，至少选择3个校准点，可参照规程给出的参考意见选择校准点，也可根据用户需求选择校准温度点，被校准表面温度计的感温元应紧密地压在表面温度源的热板中心，待示值稳定后记下读数，重复上述步骤，每个校准点的读数不得少于3次，3次的平均值与标准器的3次平均值比较，作为表面温度计的示值误差。

1 测量模型

1.1 数学模型

计算公式：x=t-（t_s+Δt_s）

式中：x——（被校）表面溫度计的示值误差（℃）;t——（被校）表面温度计的示值（℃）;ts——精密铂电阻温度计的示值（℃）;Δts——精密铂电阻温度计的修正值（℃）。

由于表面温度源控温均匀性、测量重复性等均对最终的测量结果产生影响，因此将模型细化为：

式中：[Εx（t）]——表面温度计的示值误差（℃）;[δts1]——精密铂电阻温度计及配套设备分辨力带来的影响（℃）;[δts2]——表面温度源控温不稳定对测量结果的影响（℃）;[δts3]——表面温度源中心与精密铂电阻温度计之间温差对测量结果的影响（℃）;[δts4]——表面温度源温场不均匀对测量结果的影响（℃）;[δΔts]——精密铂电阻温度计及其配套设备的温度修正值对测量结果的影响（℃）;[δt1]——表面温度计的示值读数重复性带来的影响（℃）;[δt2]——表面温度计的示值读数分辨力带来的影响（℃）。

1.2 不确定度传播率

数学模型中的各分量彼此独立不相关，则：

式中：灵敏度系数为[c1=c2=c3=]1。

2 测量不确定度的评定分析

2.1 标准不确定度分量的来源及评定

2.1.1 标准器分辨力带来的标准不确定度[uts1]

精密铂电阻温度计及其配套仪表的分辨力为0.1℃时，则不确定度区间半宽为0.05℃，按均匀分布，k=[3]，则标准不确定度为：

2.1.2 表面温度源控温不稳定带来的标准不确定度[uts2]

表面温度源控温稳定度为5min内不超过±0.05℃，不确定度区间半宽为0.05℃，按均匀分布，k=[3]，则标准不确定度为：

2.1.3 表面温度源中心与精密铂电阻温度计之间温差带来的标准不确定度[uts3]

温差最大为0.1℃，不确定度区间半宽为0.05℃，按均匀分布，k=[3]，则标准不确定度为：

2.1.4 表面温度源温场不均匀带来的标准不确定度[uts4]

根据证书，温场不均匀扩展不确定度为0.5℃，[k]=2，按正态分布，则标准不确定度为：

[uts4]=0.5/2=0.25℃

2.1.5 标准器修正值带来的标准不确定度[uΔts]

精密铂电阻温度计经过检定合格，其扩展不确定度为0.1℃，依照证书，按正态分布考虑，取置信因子[k]=2，则标准器带来的标准不确定度为：

[uΔts]=0.1/2=0.05℃

2.1.6 被校表面温度计重复性测量带来的不确定度[ut1]

表面温度计在400℃下，测量10次，测量结果分别为（单位：℃）：400.1，400.3，400.3，400.3，400.2，400.1，400.1，400.1，400.2，400.2。测量的实验标准差为：

[Sxi]=[i=1nxi-x2n-1]=0.09℃

测量结果平均值的标准不确定度为：

[ut1]=[S（xi）2]=0.06℃

2.1.7 被检表面温度计分辨力带来的标准不确定度[ut2]

被检温度计的分辨力为0.1℃时，不确定度区间半宽为0.05℃，按均匀分布，k=[3]，其標准不确定度为：

[ut2]=0.05/[3]=0.03℃

为避免重复计算，重复性和分辨力只取最大值，因此计算最大影响量[ut1]，舍弃[ut2]。

2.1.8 标准不确定度分量表

计算过程中采用的各标准不确定度分量表如表2所示。

表2 计算过程中采用的标准不确定度分量

2.2 合成标准不确定度

2.3 扩展不确定度的确定

由于表面温度源温场不均匀带来的标准不确定度大于其它标准不确定度分量合成三倍以上，为正态分布，因此在P=95%时，可取包含因子k=2，扩展不确定度为：

U=ku_c（x）=0.6℃

2.4 对使用表面温度计校准装置校准表面温度计的测量不确定度评估

1）根据JJF 1409-2013《表面温度计校准规范》的规定，常规校准应对表面温度计的3～4个测量点进行校准，即需校准100℃、200℃、300℃、400℃共4个点，其测量不确定度见表3。

2）表面温度计校准装置的测量范围为0～400℃，因此对全部校准点的测量不确定度评估如表4。

当被校表面温度计的分辨力不同时，不确定度分量中的[ut1]、[ut2]将发生改变，因此，当校准分度值为1℃表面温度计时，测量不确定度如表5。

3）对常规表面温度计各分度值按计量标准考核规范中规定不确定度要求进行评估，结果如表6。

2.5 测量结果不确定度的报告与表示

2.5.1 校准和测量能力

0.1℃分辨力的表面温度计是使用表面温度计校准装置可校准的最佳被校温度计，因此该项目的CMC为：0～400℃，U=0.6℃，k=2。

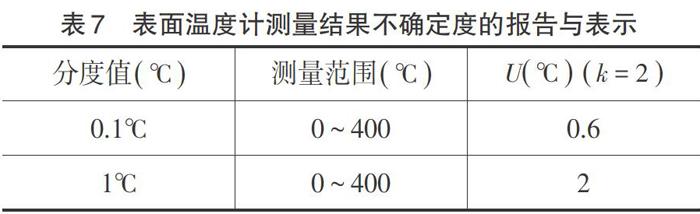
2.5.2 不确定度结果

依据计量标准考核规范中对常规仪器进行评估的不确定度结果见表7。

3 结语

本文介绍了表面温度计的用途、工作原理和校准方法，并对表面温度计的测量不确定度来源进行了分析，不确定度因素主要包括：标准器和被检表面温度计的分辨力、表面温度源控温不稳定、表面温度源中心与精密铂电阻温度计之间存在温差、表面温度源温场不均匀、标准器的修正值、被校表面温度计重复性等。通过建立测量模型，给出了表面温度计示值测量结果的不确定度的分析与评定过程，为其他同类型或相似测量仪器的不确定度的分析与评定提供了参考。

【参考文献】

[1]  测量不确定度评定与表示：JJF 1059.1-2012[S].

[2]  表面温度计校准规范：JJF 1409-2013[S].

[3]  倪育才.实用测量不确定度评定[M].北京：中国质检出版社，2016.

[4]  乔震东.表面温度计示值测量值的不确定度评定[J].计量与测试技术，2017（11）：85.

[5]  张弓.表面温度计示值误差测量结果的不确定度评定[J].计量与测试技术，2013（11）：86-87.