逐次差分代换的对偶算法

徐 嘉

(西南民族大学计算机科学与技术学院，四川 成都 610041)

逐次差分代换算法起源于非常朴素的数学思想，即“非负实数相加或相乘仍然是非负的”.最初的差分代换方法是用于证明对称不等式的.众所周知，这个方法有点类似于数学分析中著名的阿贝尔(Abel)代换(用法有所不同)，国外也有人称之为buffalo way(水牛方法或暴力方法，简称BW).一些相当困难的对称不等式可以轻易的被这个方法解决.而这些不等式(次数高变元多)是其它方法(或算法)很难处理的.有明确的资料显示，这一方法曾经被多人在正式的期刊中使用，如文献[1].但是这些仅仅只是使用方法，而不是对方法本身的研究和探讨.它的较为深刻的发展则是非常近的事.从差分代换到逐次差分代换是这一方法发展中的关键一步.这一步是在文献[2]中完成的.Yang不但引入了一般的差分代换的概念和基本代换矩阵，还编写了Maple程序SDS，用于自动探索性证明代数不等式.正是这个短程序SDS的有效性，激起了后续的进一步研究.逐次差分代换的一个明显的缺点是对不成立的不等式没有任何作用.针对这一点，杨路和姚勇在文献[3]中改进了逐次差分代换算法，使用了非常简单的思想，即在做每一次代换的同时再验证一个点处的值(通常取点 (1，…，1) 或者点 (1，0，…，0)).改进后的算法被称为TSDS，它被证明对不成立的不等式是完备判定的[3]，并且还能够自动输出反例.这个改进对探索不等式是非常有用的.因为在被证明之前，我们并不知道所研究的不等式是否成立.TSDS验证了一系列不等式猜想是不正确的，其中包括Vasc猜想[4-5]和杨学枝猜想[6].

关于逐次差分代换算法的一个重要问题是终止性问题，也就是对什么样的多项式TSDS算法会终止，输出结论.这个问题至今仍悬而未决.在双变元的情况，文献[7]中已经解决.证明了双变元的齐次多项式如果无平方因子，则算法TSDS总是终止的.同样重要的是对正定形式，逐次差分代换算法是否终止.很不幸，答案是负面的.在文献[7]中，举出了实例，说明对正定形式，逐次差分代换算法仍可能不终止.姚勇因此考虑改变基本代换矩阵，引入了带权重的基本代换矩阵[7].建立了新的差分代换算法NEWTSDS，新算法被证明对正定形式是终止的.姚勇和本文作者合作在文献[8]中证明了新算法的适用范围整体上优于著名的Polya方法的适用范围.

逐次差分代换算法被应用于证明带逻辑连词“∧”(and)的不等式命题是不难的，在证明一类根式不等式时会遇到，它已经在文献[9]中被大量使用.但是在实代数几何中，常常也会遇到带有逻辑连词“∨”(or)的命题.下面就是一个简单的例子.

考虑二次多项式

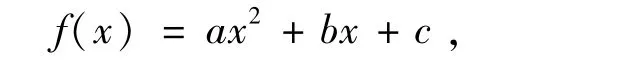
假设 a ＞ 0，c≥0，问a，b，c满足什么条件时，对任意x∈ℝ+(x≥0)，下式都成立:

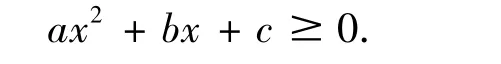
容易看到答案是:

这就是一个典型的带逻辑连词“∨”的不等式命题.如果a，b，c是常数，验证这样的命题自然不会有什么困难，可是如果a，b，c带有变量，那么这个问题就不那么简单了.例如证明下面的二次型在上是非负的(这种二次型被称为copositive二次型[10]).

容易证明条件a＞0，c≥0是满足的，按照上面的结论就还需要证明:

对任意点 (x2，x3，x4，x5) ∈ ℝ4+有

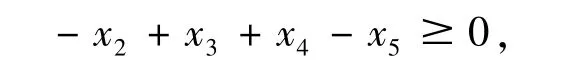
或者判别式 -x2x4+x3x4-x3x5≤0.

可是-x2+x3+x4-x5和-x2x4+x3x4-x3x5在ℝ4+上都是不定的.时而取正值，时而取负值.原来的逐次差分代换算法是不适用于证明这样的命题的.

本文的目标就是改进原来的逐次差分代换算法，使得改进后的算法可以用于证明含逻辑连词“∧”和“∨”的不等式命题.本文剩余部分内容的安排如下:第1节简单地描述了逐次差分代换算法的基本内容；第2节是新的对偶算法的建立过程；第3节是对偶算法终止性的理论结果；最后一节是算法的初步应用.

1 逐次差分代换算法的基本知识

在这一节，我们将对需要用到的基本知识作些简单介绍.本小节的主要内容来自文献[3，7，8]，也可见专著[11-13].

考虑如下n×n三角方阵

矩阵G被称为重心矩阵，如果G可以由Gn经过行置换得到.

设Sn是集合 {1，2，…，n }上的置换对称群.Pσ是置换σ对应的置换矩阵.重心矩阵也可以表示为:

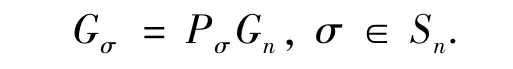
多项式f的差分代换集被定义为DS(f):

一般地，多项式f的k阶差分代换集被定义为DS(k)(f).

下面给出基于重心矩阵的逐次差分代换算法(GSDS).

算法1GSDS].输出:“正半定形式”或“非正半定形式”1)k←0；DS(k)←{f}；Temp←{}.2)删除DS(k)中系数非负的多项式后存入Temp.3)如果Temp是空集则输出“正半定形式”.4)如果 ∃g∈Temp，使得g(1，…，1) ＜ 0，则输出“非正半定形式”.5)否则:DS(k+1)← ∪输入:整系数齐次多项式f∈ℝ x1，…，xn[g(GσxT)6)k←k+1.7)程序结束.g∈Temp ∪σ∈Sn

这里的逐次差分代换算法GSDS是基于重心矩阵的.最初的差分代换是基于矩阵

只需将算法1中的矩阵Gn换为矩阵An就可得到原来的逐次差分代换算法.

算法1的正确性证明可以参看文献[7-8].由杨路和姚勇编写的程序TSDS5是算法1的Maple平台实现，可到相关网站下载该程序.

这一节只举一个应用的例子.

例1.1(arqady)已知a，b，c＞0且满足a+b+c＝1.证明:

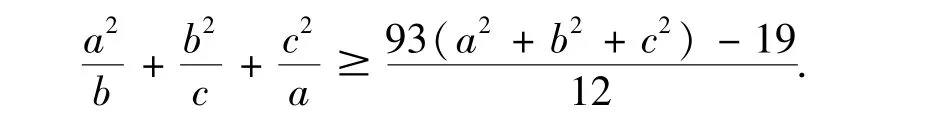
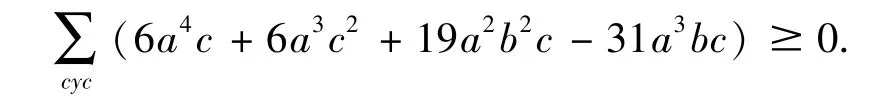
这是一个有名的形式简单，证明困难的不等式.通过去分母，齐次化，上式转变为证明:运行程序 TSDS5中的命令“TSDS”或“NEWTSDS”，都在5步代换之后终止，运行时间分别为0.063s，0.047s.输出结果为:

‘The form is positive semi-definite’也就是不等式成立.

2 对偶算法

ℝn表示n维实向量空间.其中的点用列向量表示.标准单纯形Δn由下式定义

本节中关心的是Δn上的单纯形.设B1，…，Bn是Δn上n个仿射无关的点，它们张成(n-1)维单纯形 [B1，…，Bn]Δ，即

记号“[]Δ”带下标是为了与矩阵记号“[]”相区别.而 [B1，…，Bn]是表示以B1，…，Bn作为列的矩阵 .记x＝(x1，…，xn)T，则单纯形可以表示为更简洁的形式

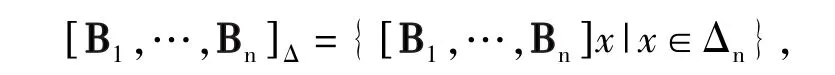
这就是单纯形的顶点表示法.

可以通过重心矩阵来表达标准单形的重心剖分，也就是

这里记号 [ Gσ]Δ表示矩阵Gσ的列所张成的单纯形，下同.

下面的引理来自文献[7-8].

引理2.1 多项式f∈ℝ[x1，…，xn]，则有如下等价关系成立

这个引理是逐次差分代换算法的基础.重心矩阵的集合

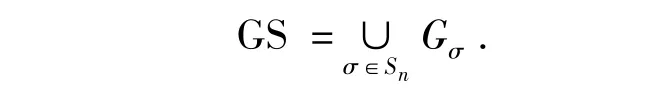
一般地，定义GS(k)

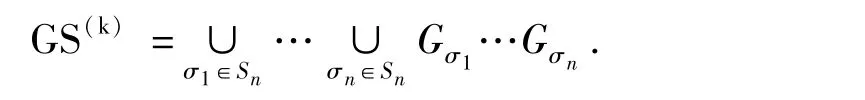
仿照算法1有算法2.

?

?

接下来比较算法1和算法2的不同点.

算法1中的局部变量Temp存储的是多项式，而算法2中的局部变量Temp存储的是单纯形 (或代换).换句话说，在算法1中，代换始终保持不变，多项式在不停的变化.在算法2中，给定的多项式始终不变，代换却在不停的变化.可以明显的看到，算法1能完成的任务，算法2仍然可以.

下面考虑一组带有逻辑连词“∧”(and)和“∨”(or)的多项式集合.

对形如

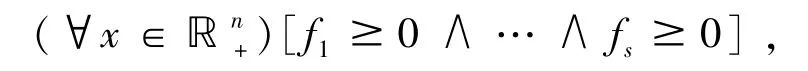
的公式，明显算法1和算法2都是适用的.下面主要考虑形如

的公式.为了使算法2能够适用于判断公式Φ是否成立，还需对算法2做一点小的修改.

?

?

说明:

①算法3中的矩阵Gσ也可换为An以获得同最初的逐次差分代换类似的改进算法.它也是有应用价值的，见例4.1.

②算法3的基本思想仍然是明显的.根据重心剖分的基本性质，每循环一次，单纯形的直径将减小1/3.因此算法3记录的单纯形，随着循环次数的增加，将变得非常小，渐渐趋近于一些点.粗略的看这就相当于将点代入多项式，来观察多项式系数的变化规律.

③算法3的正确性是明显的.它的终止性同算法1一样可能不终止.它的适用范围明显比算法1大了很多.下一节将证明算法3关于终止性的理论结果.

3 主要理论结果

在这一节将要证明两个关于算法3的终止性的定理.

定理3.1 f1，…，fs∈ ℝ [x1，…，xn] 是齐次多项式，给定公式:

如果存在点P∈Δn，使得公式Φ不成立，则算法3是终止的，并且输出“false”.

证明:假设点P∈Δn使得公式Φ不成立，也就是P满足

由多项式函数的连续性，我们知道存在点P的一个邻域O(P，ε)，这个邻域中的点都满足

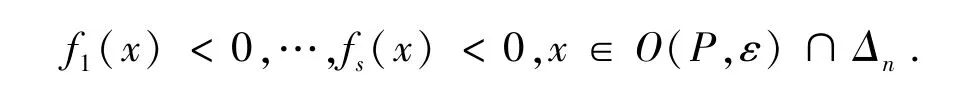
根据重心剖分的基本性质，算法3每循环一次，单纯形的直径将减小1/3.随着循环次数的增加，单纯形将变得非常小，渐渐趋近于一些点.因此对充分大的k，存在单纯形

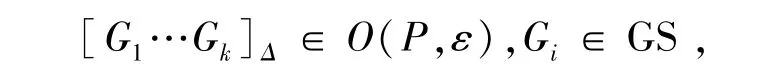
此时有:

也就是算法3最多经k次循环将输出 “false”.

定理3.2f1，…，fs∈ℝ [x1，…，xn] 是齐次多项式，给定公式

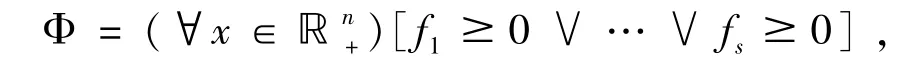
如果对任意点P∈Δn，都有

则算法3是终止的，并且输出“true”.

证明:这里的证明依赖于Δn的紧致性和文献[8]中的主引理.

不失一般性，可以假设给定点P对某个固定的i成立

(注意，这里对不同的P，多项式fi可能是不同的)由多项式函数的连续性，我们知道存在P的一个邻域O(P，ε)，这个邻域中的点都满足

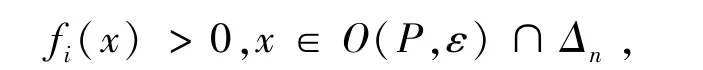
也就是说，在邻域O(P，ε)内下面公式是真命题

由于点P的任意性，对Δn的每一点选择一个邻域，可以得到Δn的一个开覆盖，根据有限覆盖定理，可以选出有限个邻域盖住Δn.因此当对Δn进行充分多阶的重心剖分后，每一个细小单形将被某个邻域盖住，不妨设单形:

如果fi(G1…Gkx)的系数都是非负的，则结论已经成立.如果fi(G1…Gkx)的系数中还含有负数，按假设fi在小单形为[G1…Gk]Δ上的值是严格正的，则根据文献[7]中的主引理，单形为[G1…Gk]Δ可以进一步细分，使得[G1…Gk]Δ的有限次重心剖分的每一个小单形[Λ]Δ⊂[G1…Gk]Δ都有fi(Λx)的系数是非负的.也就是，算法3最终将输出“true”.

下面的定理是定理3.1和定理3.2的明显推论.

推论3.3f1，…，fs∈ℝ [x1，…，xn] 是齐次多项式，给定公式

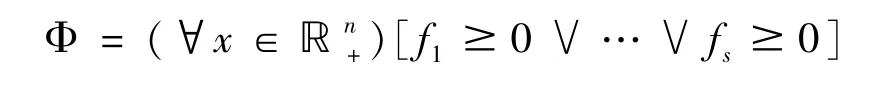
如果算法3不终止，则所给定的公式Φ是真命题.

推论3.3表明对:

这类命题算法3是半可判定的.

4 应用

现在来应用算法3.

例4.1证明∀(a，b，c，d) ∈ Δ4如下公式成立

证明:考虑矩阵

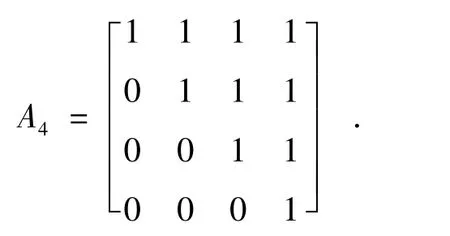
对称群S4有24个元素.所以，初始的GS(0)中有24个矩阵.

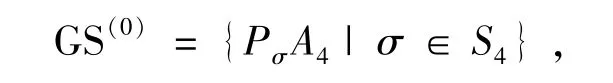
记f1＝b+c-a-d，f2＝ac+bd-bc.首先计算

f2所有的系数全是正的.所以，将A4从GS(0)中删除.同样计算全部24个矩阵发现:

f1(PσA4(a，b，c，d)T) ， f2(PσA4(a，b，c，d)T) ，中至少有一个是系数全是正的，所以Temp是空集.程序输出“true”后停止.

例4.1比较简单，程序运行了一次循环就停止了，证明了公式是成立的.下面将考虑困难得多的问题:

在文献[5]中提出了如下公开问题:

例 4.2a，b，c是正实数. 证明

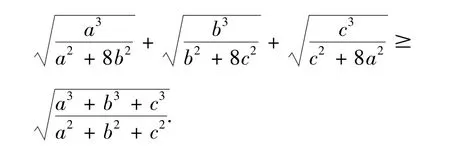
为了解决这个问题，需要如下引理，它来自文献[14].

引理4.3u，v，w，t是正实数，则下面等价关系成立

其中

例4.2的证明:令

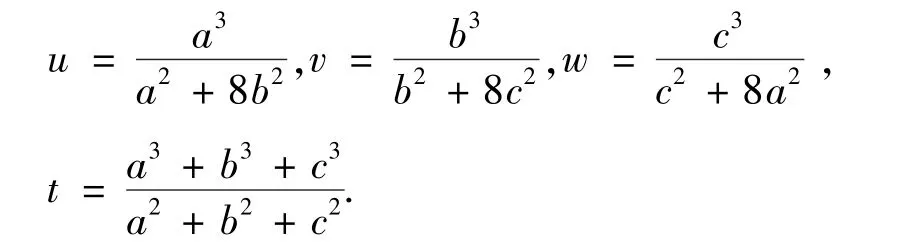
代入R1，R2，R3.通过去分母，转化为三个齐次多项式，分别有次数 9，18，36. 其中具有424项，最大系数为235583387168.

通过引理4.3，还需要证明如下公式成立

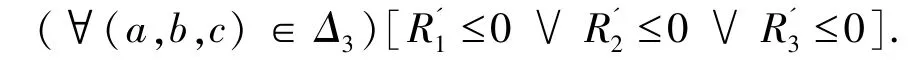
在Maple平台编程，算法3在运行了7次循环之后终止，输出了结果“true”.用时74s.

讨论:例4.2的方法可以被应用于更加广泛的型如

不等式的机器证明.

现在考虑带有量词"∃"的命题.注意到公式

等价于

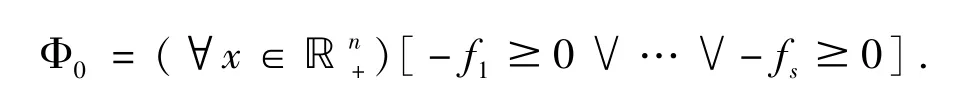
因此算法3可以被应用到寻找满足一组不等式的特解问题.恰好配平方和就可以归结到这样的问题.下面仅举一个简单的例子.

例4.3请给出多项式

的平方和表示.

根据Gram矩阵方法，问题可以归结到寻找实数a使得如下的矩阵C(f)是半正定的矩阵.

计算它的特征多项式

矩阵C(f)是半正定的等价于T(z)的根都是非负实数.也就是a需要满足不等式组

把条件放宽一点，a，b＞0满足如下严格不等式是足够的.

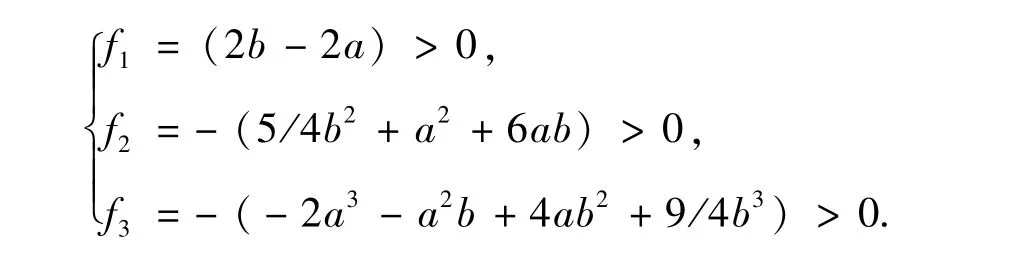
这样就转化为了

a分两部分a≥0，a＜0.分别求解上面的公式.使用算法3，仅仅循环了一次就获得了一个解

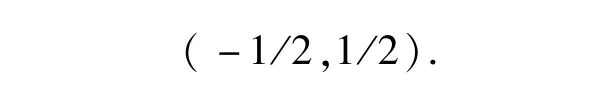
回到不等式(4.1)，a＝-1是一个解.因此得到一个半正定矩阵

分解为C(f)＝BBT，

最后获得平方和表示为

[1]AN ZHENGPING.Some Techniques for Proving Inequalities[J].High-School Mathematics，1995，5:7-10.

[2]YANG LU.Solving Harder Problems with Lesser Mathematics.Proceedings of the 10thAsian Technology Conference in Mathematics[C].ATCM Inc，2005:37-46.

[3]YANG LU，YAO YONG.Difference Substitution Matrices and Decision on Nonnegativity of Polynomials[J].Journal of Systems Science and Mathematical Science，2009，29(9):1169-1177.(in Chinese).

[4]VASILECIRTOAJE.Algebra Inequalities:old and new methods[M].Zalau:GIL Publishing House，2006，46.

[5]VASILECIRTOAJE，VO QUOC BA CAN，TRAN QUOC ANH.Inequalities with Beautiful Solutions[M].Zalau:GIL Publishing House，2006.

[6]YANG XUE ZHI.Research on Mathematical Olympiad inequalities[M].Harbin，Harbin Institute of Technology Press，2009.(in Chinese).

[7]YAO YONG.Infinite product convergence of column stochastic mean matrix and machine decision for positive semi-definite forms[J]，Science China Mathematics ，2010，40(3):251-264.

[8]XU JIA，YAO YONG.Polya’s Method and the Successive difference substitution Method[J].Scientia Sinica Mathematica，2012，42(3):203-213.(in Chinese).

[9]XU JIA，YAO YONG.Rationalizing Algorithm and Automated Proving for a Class of Inequalities Involving Radicals[J].Chinese Journal of Computers，2008，31(1):24-31.(in Chinese).

[10]徐嘉，李高平.copositive二次型与copositive矩阵[J].西南民族大学学报(自然科学版)，2011，37(4):504-508.

[11]YANG LU，XIA BI CAN.Automated Proving and Discovering on Inequalities[M].Beijing:Science Press，2008.(in Chinese).

[12]XIA BI CAN，YANG LU.Automated Inequality Proving and Discovering[M].Singapore:World Scientific Publishing Co.Pte.Ltd.，2016.

[13]WANG WAN LAN.Approaches to Prove Inequalities.Harbin，Harbin Institute of Technology Press，2011.(in Chinese).

[14]徐嘉.三类根式不等式的有理化与机器证明[J].西南民族大学学报(自然科学版)，2016，42(2):200-206.