高强汽车板高速拉伸数值模拟及验证

文／王秋雨，张琳·河北钢铁集团唐钢分公司

汽车碰撞过程中材料变形是高应变的动态过程，其应变速率分布在10-1～103s-1之间，车辆碰撞安全可靠性分析对材料在高应变速率条件下的力学行为提出了评测需求。可靠的材料模型是有限元仿真的基础，碰撞问题的有限元仿真涉及到材料在动态载荷作用下的弹塑性本构关系，另外，汽车主机厂的材料认证也要求提供材料动态拉伸力学性能数据，因此，有必要开展汽车板材料动态力学行为研究，建立与变形率相关的材料模型。

本文对现有动态拉伸数据进行了整理分析，用HyperMesh前处理软件生成Ls-Dyna材料库文件，根据试验条件建立高速拉伸仿真模型，通过对比不同应变速率下应力-应变的仿真结果与试验结果，验证所建立的材料变形速率相关模型的可行性和适用性。

模型情况及基本假设

几何模型的建立

高速拉伸试样尺寸如图1所示，利用HyperMesh前处理软件对试样建立动态拉伸试验的数学模型，如图2所示，其中平行段的网格尺寸为0.2mm，其他部分的网格尺寸均为0.4mm，为保证计算的准确度，所有网格均采用规则六面体网格。

边界条件及假设

拉伸试样的右端面（图2中绿色部分）固定，左端面（图2中粉色部分）以恒速进行拉伸，为了保证标定段均匀变形，该速度为拉伸试验机的横梁速度。本文模拟所采用的材料变形速率分别为0.1s-1、1.0s-1、10s-1、100s-1、500s-1、1000s-1。横梁速度V=ε［(mS0/CM）+Lc］，式中：ε为试样的应变速率，单位为s-1；m为试样的弹性模量，单位为MPa；S0为试样原始的横截面积，单位为mm2；CM为试验装置中夹具的刚度，单位为N/m；Lc为试样平行段的长度，单位为mm；V为横梁的运动速度，单位为mm/s。

由于在试验过程中，试验装置的弹性变形量很小，因此，由试验装置引起的横梁运动速度值变化可以忽略不计。横梁运动速度的公式可简化为V=Lc·ε，根据该公式，计算得到仿真模拟时所采用横梁的运动速度，如表1所示。

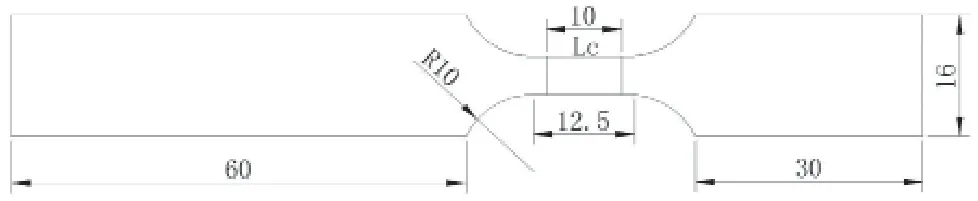
图1 高速拉伸试样尺寸

图2 利用HyperMesh软件建立的高速拉伸数学模型

材料模型

试验材料为唐钢的CR340/590DP冷轧钢板，厚度为1.4mm，CR340/590DP的基本力学指标如表2所示。

汽车安全碰撞的过程是与材料的应变速率相关的动态过程，在碰撞模拟过程中要输入材料动态参数，以获得准确的输出结果。在Ls-Dyna软件中，与材料动态参数对应的材料模型为24号弹塑性材料模型。

利用HyperMesh软件建立与Ls-Dyna软件相对应的24号弹塑性材料模型，24号材料模型如表3所示。HyperMesh软件中反映材料动态应力应变关系的方程为Cowper-Symonds本构方程和表格LCSS两种形式。采用清华大学拟合的Swift-Hockett-Sherby本构数据，以表格的形式建立CR340/590DP的材料数据库。

最后，将由HyperMesh软件生成的数学模型转化成材料文件，在Ls-Dyna软件中进行计算处理，并观察计算结果。

高速拉伸试验

技术方案

测试项目包括每种材料在准静态和动态共6个变形速率（0.1s-1、1s-1、10s-1、100s-1、500s-1、1000s-1）下进行单向拉伸试验，试验时均右端固定，左端以一定的速度进行拉伸，其横梁的运动速度与表1一致，每次试验重复3次。在进行动态拉伸试验前，先取0°、45°、90°三个方向的试样进行静态拉伸试验，确定强度最弱的方向。然后取最弱方向的试样进行不同变形速率下的动态拉伸试验。动态拉伸和准静态拉伸试样尺寸分别如图1、图3所示。

图3 准静态拉伸试样尺寸

表1 高速拉伸仿真所采用横梁速度

表2 CR340-590DP的基本力学性能

表3 Ls-Dyna软件中的24号材料模型

图4 拉伸试验的主要试验设备

试验设备

主要试验设备如图4所示，主要包括：

⑴ 电子万能试验机，试验机量程为50kN，测试速度范围为0.001～500mm/min，主要用于准静态测试。

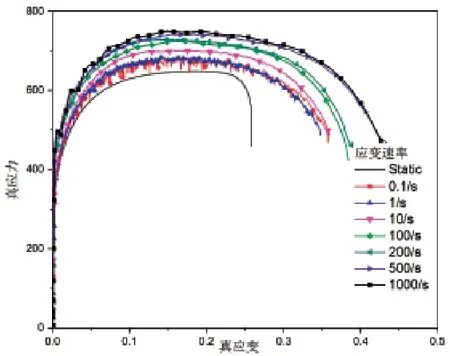
图5 静态和动态拉伸试验得到的真应力-真应变曲线

⑵ 高速拉伸试验机，试验机量程为50kN，测试速度为0.001～20m/s，用于钢板的动态测试。

⑶ 低速/高速摄像机，拍摄准静态和动态试验过程中的试样二维变形（1台摄像机）。

⑷ 非接触变形测量分析系统，分析试验录像，计算试样静态/动态变形。

数据处理

根据拉伸试验数据做工程应力-应变曲线，由工程应力-应变曲线转化得到不同应变速率下的真应力-真应变曲线（图5）。由图5可以看出，随着变形速率的增大，应力-应变曲线呈递增趋势。这是因为随着变形速率的增大，变形时间越短，金属的动态回复和再结晶越不充分，加工硬化作用越显著。

仿真模拟结果及对比

模拟结果

现以变形速率1000s-1为例，介绍动态拉伸试验的模拟过程及结果，如图6所示。

图6 变形速率为1000s-1时出现缩颈前的应力应变分布图

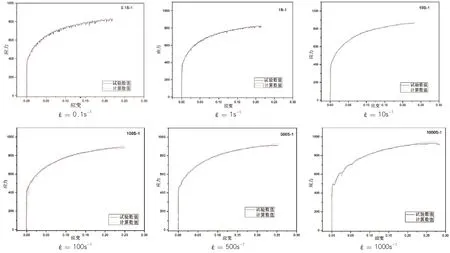
图7 不同应变速率下应力-应变曲线的仿真结果与试验结果对比

由图6可以看出，在试验出现缩颈之前，试样的平行标定段处于均匀变形阶段，即平行标定段各个节点的真应力和塑性应变数值相同。因此，与试验数值进行对比分析时，可以跟踪平行标定段的任何一个节点。

仿真模拟数值与试验对比分析

应变速率为0.1s-1、1s-1、10s-1、100s-1、500s-1、1000s-1时，跟踪平行标定段上某个节点的应力应变变化情况，绘制出缩颈前的应力-应变曲线，并与试验得到的真应力-真应变曲线进行对比，对比结果如图7所示。

由图7可以看出，模拟得到的各应变速率下的真应力-真应变曲线与试验得到的真应力-真应变曲线吻合性很好，这说明利用HyperMesh软件建立的24号与变形速率相关的弹塑性材料模型具有可靠性和可行性。

结论

⑴ 将各应变速率下Swift-Hockett-Sherby本构拟合数据以表格的形式输入到Ls-Dyna软件24号材料模型中，模拟不同应变速率下的高速拉伸过程，模拟结果表明，在出现缩颈前，平行标定段各节点处于均匀变形阶段。

⑵ 不同应变速率下的应力-应变曲线模拟仿真结果与试验结果吻合良好，说明建立的材料模型具有可靠性和可行性。